基于循环自相关/平均幅度差函数的弹道目标微动周期估计

金家伟， 阮怀林

(国防科技大学电子对抗学院， 合肥， 230031)

在弹道中段的飞行过程中，为了保持飞行的稳定性，弹头一般会进行姿态控制，不仅会绕自身对称轴作自旋运动，还会受到冲击力矩的作用，力矩消失后对称轴将在平衡位置做圆锥运动，即进动[1]。而诱饵一般不具备姿态控制装置，因此，进动是中段弹头特有的微动方式，与目标形状结构、质量分布以及动力学特性等物理属性密切相关[2]。由微动引起的雷达回波中多普勒频率的调制，一般被称为微多普勒效应[3]。微多普勒特征体现出目标独特的动态和结构特征，在目标识别和分类方面具有巨大的潜力[4-5]。

对于非刚性雷达目标，目标主体散射的雷达回波占返回能量的绝大部分，微动信号始终浸没在主体雷达回波中，需要将雷达回波分解为平动分量和微动分量，用微动分量来估计微多普勒参数[6-8]。文献[9]对信号进行小波变换，用分解出的微动分量的自相关来估计振动/旋转速率；文献[10]通过信号分解提取单个散射点特征。而为了表示出散射点雷达回波的时变频率调制特性，时频分析被广泛用于分析微多普勒特征，基于时频分布的微动参数估计已成为微多普勒特征提取的重要部分。文献[11]采用基于加权迭代自适应的时频分析方法结合逆Radon变换，分离重构不同散射点的微多普勒分量；文献[12]利用短时分数阶傅里叶变换分离肢体和躯干的微多普勒信号；文献[13]结合Gabor时频分布和变分模态分解，来估计目标的自旋频率和锥旋频率。

上述方法都需要假设目标平动已被准确补偿，在此前提下，目标时频分布中的微多普勒频率曲线通常应该表现为正弦曲线[3]或是多个正弦分量的合成[2]。现有的微多普勒特征提取技术，如经验模式分解(empirical-mode decomposition, EMD)[14]和扩展Hough变换(extended hough transform,EHT)[15]，主要依赖于这种正弦调制假设。但目标运动由平动与微动复合而成，特别是对于高速运动的弹道目标，周期进动引起的弹道目标微多普勒效应并不像通常那样表现为正常的正弦调制[16]。

针对目标微动伴随平动时，时频分布不再表现为正弦调制曲线，本文在雷达回波信号时频分布的基础上，结合循环自相关函数(circular autocorrelation function，CACF)和循环平均幅度差函数(circular average amplitude difference function，CAMDF)，以获取时频分布的循环系数矩阵，并通过该矩阵的平均循环系数估计出弹道目标的微动周期。

1 模型建立

空间进动锥体目标模型如图1所示，坐标系(U,V,W)为雷达坐标系，雷达静止于原点Q。O为目标质心，以O为原点、目标对称轴Oz为z轴建立目标本体坐标系O-xyz。以O为原点建立参考坐标系O-XYZ，以初始时刻与目标对称轴Oz、进动轴OZ共面且垂直于OZ的方向为Y轴，X轴根据右手准则确定。目标在平动的同时，以角速度ωs绕对称轴z轴做自旋运动，同时以角速度ωc绕轴OZ做锥旋运动(ωs和ωc均采用参考坐标系中的表达式)，自旋轴和锥旋轴之间的夹角为进动角θ。

图1 目标模型

在光学区，雷达目标的整体散射特性通常可以等效为若干个散射中心的叠加。为不失一般性，我们假设目标的微动是周期性进动，目标的平动是任意且未知的。假设目标等效为K个散射中心，各散射中心各向同性，雷达发射的电磁波为连续单频波，载频为f0。考虑目标的平动，第i个散射中心与雷达之间的距离为：

ri(t)≈rT(t)+rMi(t)

(1)

式中：i=1,2，…，K，为散射中心序号；rT(t)为目标平动对应的距离；rMi(t)为第i个散射中心微动对应的距离。从式(1)可以看出，散射中心的总体运动由锥体目标平动和散射中心微动合成，表现在距离上是周期性的正弦运动叠加一个平动趋势项。由文献[3]可知：

rMi(t)=rMi(t+TM)

(2)

式中：TM为目标的进动周期。雷达向由i个散射点组成的目标发射电磁波，返回的基带信号表示为：

sT(t)sM(t)

(3)

其中：

(4)

(5)

σi(t)=σi(t+TM)

(6)

由式(2)和式(6)可得：

sM(t)=sM(t+TM)

(7)

第i个散射中心的瞬时多普勒频率为：

(8)

(9)

(10)

fMi(t)为目标第i个散射中心的微多普勒频率，fT(t)为目标的平动多普勒频率，可以被建模为多项式函数[17]如下：

fT(t)=c0+c1t+c2t2+…+cLtK

(11)

2 雷达微动信号的时频分析

由式(7)可知，微动信号有着与进动相同的周期，目标周期性的进动对雷达回波进行了周期性的时变频率调制。时频分析可以描述信号的频率随着时间变化的规律，因此可用来体现进动目标微多普勒效应的周期性。短时傅里叶变换(STFT)是时变信号的线性时频表示，为简单起见，这里使用STFT来证明微动信号时频分布的周期性：

ρM(t,f)=

(12)

下面分析式(12)的周期性，令t=t+TM，由于sM(t)=sM(t+TM)，可得：

ρm(t+TM,f)=

(13)

令τ=τ1+TM，可得：

ρM(t+TM,f)=

exp(-j2πfTM)ρM(t,f)

(14)

因此，可得：

|ρM(t+TM,f)|=|ρM(t,f)|

(15)

周期进动引起的微动信号的时频分布与进动具有相同的周期，式(15)的离散形式为：

|ρM(n+NT,m)|=|ρM(n,m)|

(16)

式中：t=nΔt,n=0,1,…，N-1；f=mΔf,m=0,1,…，M-1,Δf=fs/M，Δt是采样间隔，fs是采样频率；NT=[TM/Δt]，[ ]表示将元素四舍五入为最接近的整数。

当存在平动时，由式(3)可知雷达回波s(t)=sT(t)sM(t)，其STFT为：

(17)

ρ(t,f)的离散形式为ρ(n,m)，则根据文献[18]可知：

|ρ(n+NT,m)|=

(18)

3 微动周期估计

CACF和CAMDF都能独立进行周期估计[17]，但如果将两种方法组合，可更为充分地体现出微动信号的周期性，并且会有更强的稳定性，文献[19]通过合成CACF和CAMDF来估计弹道中段目标的RCS周期。当雷达目标存在平动时，虽然雷达回波信号的时频分布并不表现为正常的正弦调制形式，但雷达回波信号的循环周期性仍然存在，本文正是利用这一特性，将时频分布的CAMDF的倒数和CACF相乘，来估计弹道目标的进动周期。

首先，分别定义ρ(n,m)2个时间切片n1和n2的循环自相关函数CACF[18]和平均幅度差函数CAMDF[20]如下：

Cr(k;n1,n2)=

(19)

Ac(k;n1,n2)=

(20)

然后构造新的函数，定义时间切片n1和n2的CACF/CAMDF如下:

(21)

令n2=n2+NT，可得：

FCC(k;n1,n2+NT)=

(22)

将式(18)代入式(22)得：

FCC(k;n1,n2+NT)=

(23)

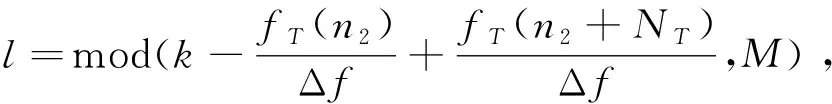
n1,n2+NT)=

(24)

由式(21)和式(24)可得:

FCC(k;n1,n2)=

n1,n2+NT)

(25)

由式(25)可以看出，FCC(k;n1,n2)是FCC(k;n1,n2+NT)的循环移位，并且CACF/CAMDF保持了ρ(n,m)的循环周期性。

然后，基于CACF/CAMDF定义ρ(n,m)的循环系数矩阵为:

MF=

(26)

式中：Cm(n1,n2)是Cr(k;n1,n2)的归一化最大值，Am(n1,n2)是Ac(k;n1,n2)的归一化最小值，即：

(27)

由Fm(n1,n2)的定义，可得:

(28)

特别地，当n2=n1+aNT(a=0,1,…)时，Fm(n1,n2)=0，所以很容易可以看出Fm(n1,n2)与Fm(k;n1,n2)具有相同的周期，即：

Fm(n1,n2)=Fm(n1,n2+NT)

(29)

因此，ρ(n,m)的循环系数矩阵保留了行和列维的周期性，并且在同一对角线上的滞后是常数。

最后，将循环系数矩阵MF第k个对角线的平均值定义为平均循环系数，即：

(30)

其中：

diag(MF,k)={MF(n1,n2),

n2=n1+k,1≤n1≤N,1≤n2≤N}

(31)

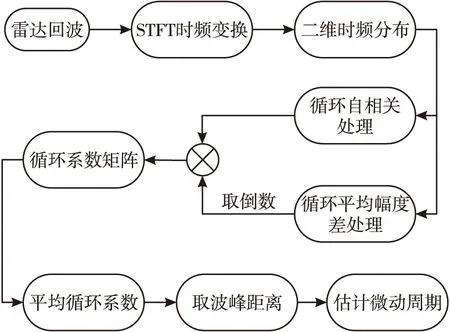
图2 算法实现流程

4 实验与分析

下面通过仿真验证本文提出的CACF/CAMDF的估计效果和抗噪性能，并将其与CACF、CAMDF进行对比。首先分别在目标的平动被补偿、目标存在平动条件下，对比3种算法的平动敏感性；然后加入不同信噪比的噪声，进一步对比3种算法在低信噪比条件下的估计性能。

仿真条件：假设雷达工作在10 GHz，且雷达坐标系中本体坐标系原点O的坐标为(400,500,100)km，本地坐标系和参考坐标系之间的初始欧拉角(x-y-z序列)为(30°,60°,45°)。假设目标绕z轴旋转，目标上有2个散射点：第一散射点A位于锥顶，在本体坐标系中的坐标为(0,0,1)m；第二个散射点B位于锥底的尾翼，在本体坐标系中的坐标是(0.5,0,-0.5)m。雷达照射时间为8 s。旋转频率为fs=1 Hz，圆锥运动频率为fc=0.5 Hz。当目标存在平动时，其平动模型为rT(t)=-vt+0.4t2+0.5t3。

4.1 平动敏感性分析

当不存在噪声时，图3给出了平动被补偿和存在平动两种情况下的雷达回波STFT时频分布图。

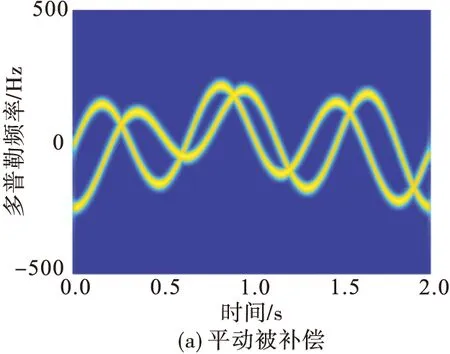
图3 无噪声条件下的时频分布

由图3可知，当平动被完全补偿时，雷达回波的时频图是多个正弦分量合成的类正弦曲线，如图3(a)所示；而时频图在目标平动的调制下，其图形不再表现为正常的类正弦曲线，如图3(b)所示。此时，CACF/CAMDF的估计结果如图4所示，其中图4(a)和图4(b)分别为时频分布的循环系数矩阵和平均循环系数。

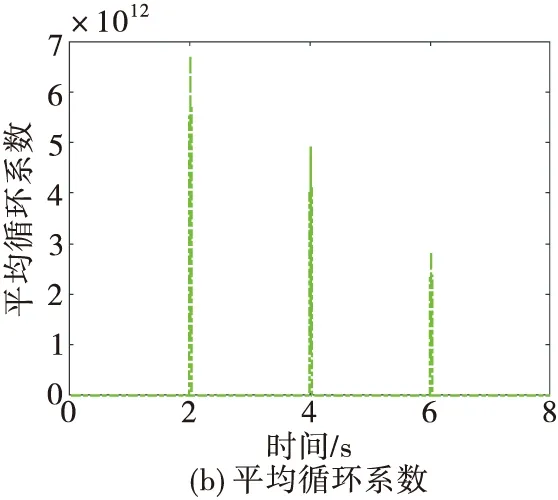
图4 平动被补偿、无噪声时的CACF/CAMDF估计结果

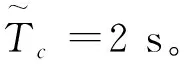
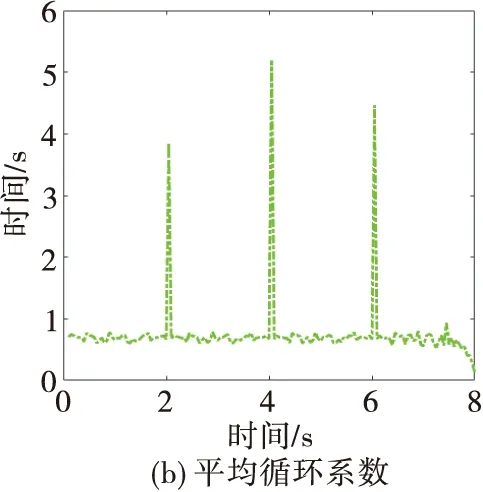
图5 存在平动、无噪声时的CACF/CAMDF估计结果

当目标存在平动时，其他条件相同，图6分别给出了CAMDF和CACF的估计结果。将图6与图5对比可看出，在平动条件下，CAMDF和CACF两种算法都具有一定的估计能力，且CACF性能更好，但性能都劣于CACF/CAMDF。这说明了CACF/CAMDF具有更低的平动敏感性，能够在目标存在平动时，具有更好的估计性能。

图6 存在平动、无噪声时CAMDF、CACF的平均循环系数

4.2 抗噪性能分析

为进一步验证CACF/CAMDF在噪声条件下的表现，分别向目标信号中添加不同信噪比的高斯白噪声进行仿真。由图7可知，即使信噪比低至-5 dB，STFT仍然能够较好地获取雷达回波的时频分布。

图7 噪声环境下存在平动时的时频分布

由图5和图8对比可知，本文算法在噪声环境下具有良好的表现。

图8 存在平动、SNR=5 dB时的CACF/CAMDF估计结果

为进一步分析算法的抗噪性能，图9给出了不同信噪比条件下、目标存在平动时的CACF/CAMDF平均循环系数图。分析图9可知，该算法具备良好的抗噪性能。即使目标存在平动、信噪比低至-2 dB，仍可准确估计出目标的进动周期。

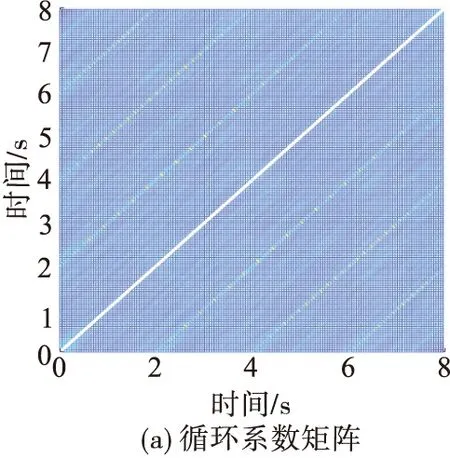
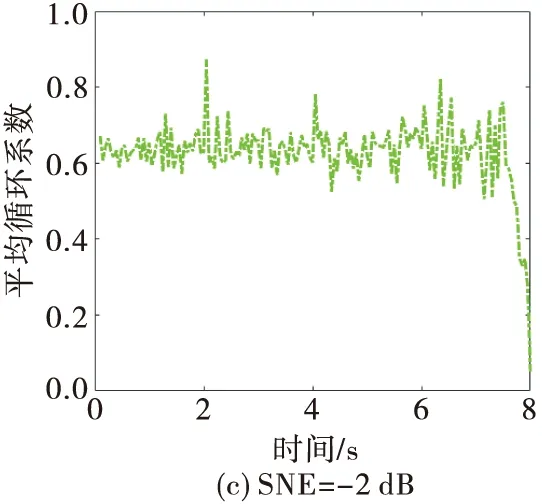
图9 存在平动时CACF/CAMDF的平均循环系数

目标存在平动时，图10和图11分别给出了不同信噪比条件下CAMDF和CACF的估计结果。对比图9～图11可知，噪声环境下，CAMDF的性能极限是2 dB，CACF的性能极限是0 dB，与CACF/CAMDF的-2 dB都具有较大差距。这进一步体现了CACF/CAMDF在低噪声环境中的性能优越性。

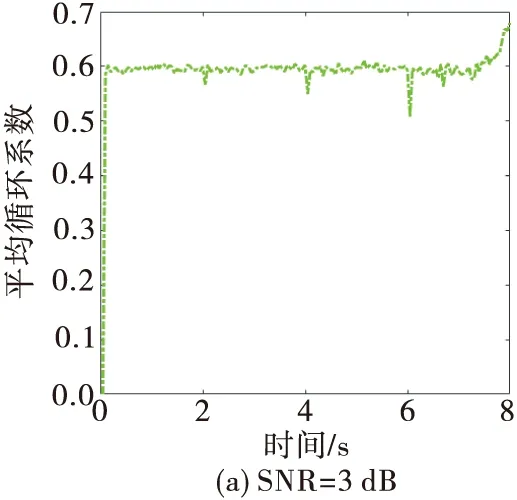
图10 存在平动时CAMDF的平均循环系数

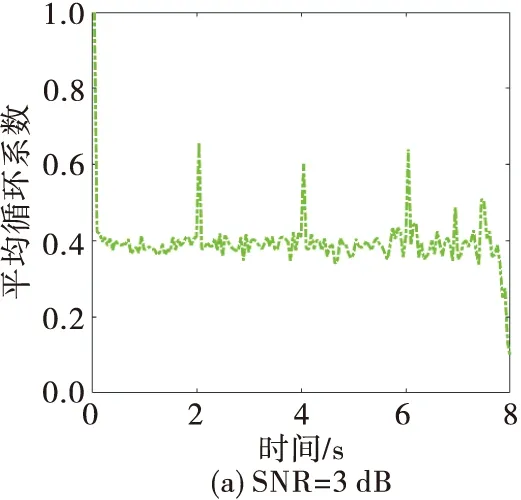
图11 存在平动时CACF的平均循环系数

5 结语

本文分析了微动和平动对雷达回波时频分布的影响，结合CAMDF和CACF，在时频分布的基础上提出了基于CACF/CAMDF的估计算法。仿真实验表明，该算法在目标存在平动的情况下，无需补偿平动分量可以直接估计微动周期，且估计性能优于CAMDF和CACF，这在信噪比较低时体现得更加明显。