组配角接触球轴承的预紧力及刚度

李红涛，张振强，张伟，宁晋，张晓杨

(1.空军装备部驻洛阳地区第二军事代表室，河南 洛阳 471009；2．洛阳轴承研究所有限公司，河南 洛阳 471039；3．河南省高性能轴承技术重点实验室，河南 洛阳 471039；4．高性能轴承数字化设计国家国际科技合作基地，河南 洛阳 471039；5．洛阳LYC 轴承有限公司，河南 洛阳 471039)

单套角接触球轴承的承载能力和刚度有限，在实际应用中往往多联组配使用。文献[1-2]提出了相同接触角轴承组配预紧力和刚度的计算方法，但参与组配的轴承也可能具有不同的接触角[3-5]，组配方式不同，组配轴承所需的预紧力及刚度也不同。文献[3]虽对不同接触角轴承组配的预紧力有所研究，但未涉及组配后的轴承刚度，且文献[1-3]均只针对具有15°或25°接触角的轴承进行分析，不具有通用性。鉴于此，基于文献[6-8]的经验，对组配轴承所需预紧力及刚度的计算通式进行分析。

1 单列角接触球轴承轴向刚度

在轴向载荷Fa作用下，单列角接触球轴承的轴向位移如图1所示，Fa与轴向位移δa的关系为[1]

(1)

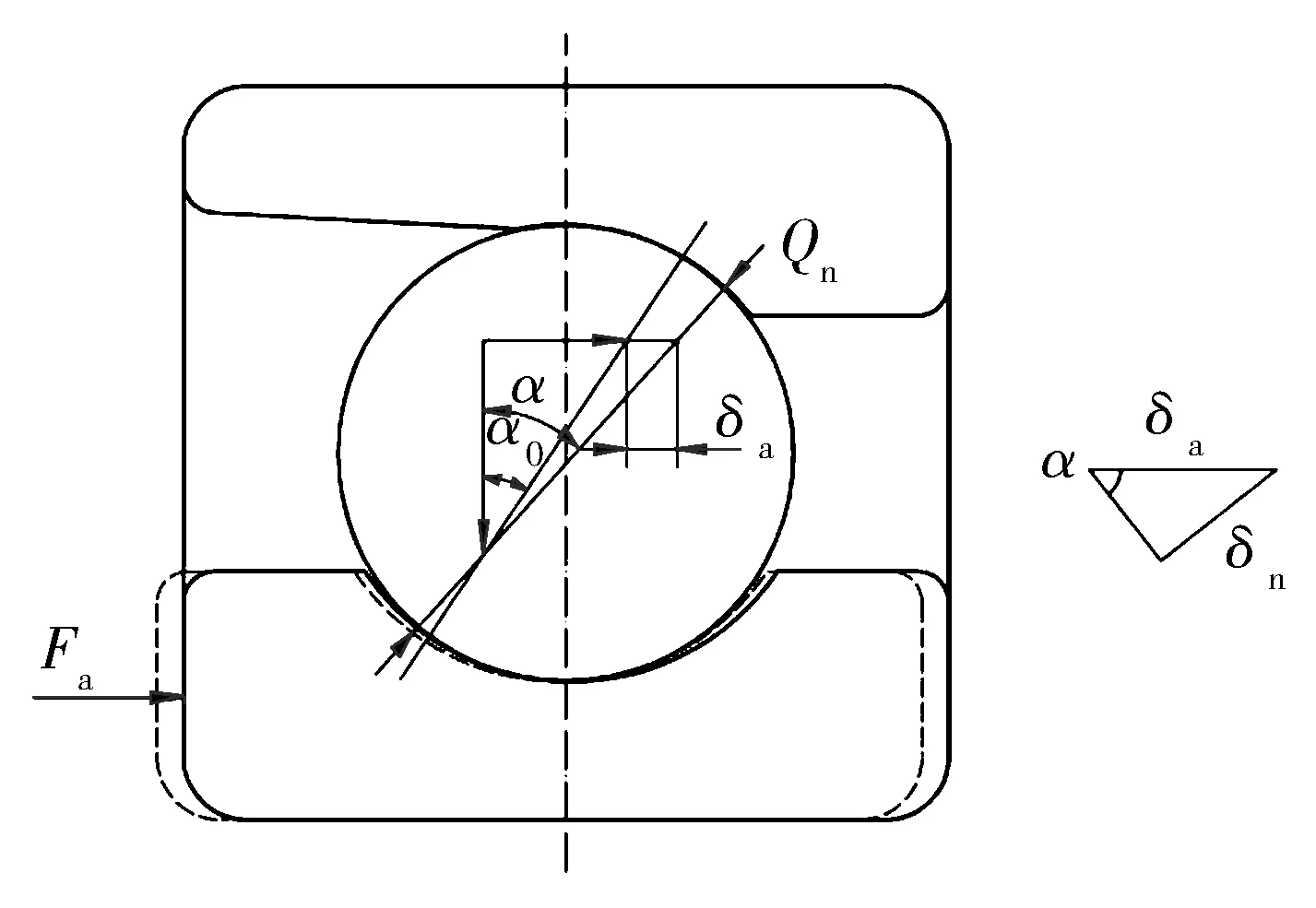
图1 角接触球轴承轴向位移示意图

式中：Z为球数；Qn为单个球的法向接触载荷；α为轴承实际接触角；kn为载荷-位移系数，与轴承的材料和几何尺寸有关。

由(1)式可得轴向位移δa为

(2)

将轴向载荷对轴向位移求导可得轴向刚度Ka，即

(3)

将(2)式代入(3)式可得

(4)

2 组配角接触球轴承轴向刚度

DB组配型轴承预紧及位移如图2所示，在预紧力F0作用下，1#轴承产生轴向位移δ0A，此时其实际接触角为αA、轴向刚度为K0A，2#轴承产生轴向位移δ0B，此时其实际接触角为αB、轴向刚度为K0B。同时可得

F0=K0Aδ0A=K0Bδ0B，

(5)

则

(6)

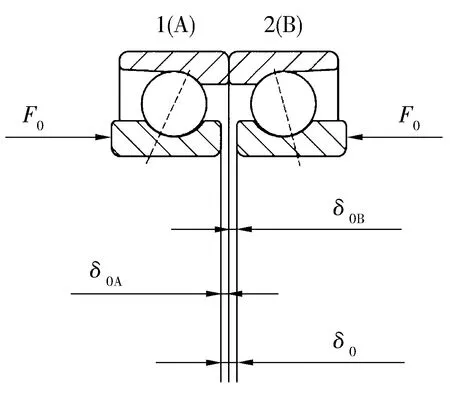
图2 DB组配型轴承预紧及位移图

令

δ0A+δ0B=δ0,

(7)

联立(6)，(7)式可得

(8)

(9)

DB组配型轴承加载示意图如图3所示，在外部轴向载荷F作用下轴承内圈相对外圈(外圈固定)产生轴向位移Δδ0A,Δδ0B(Δδ0A=Δδ0B),此时各轴承所受外部轴向作用力分别为

FA=F0+K0AΔδ0A，

(10)

FB=F0-K0BΔδ0A，

(11)

轴承组的实际载荷增量为

ΔF=FA-FB=K0AΔδ0A+K0BΔδ0A，

(12)

两联组配轴承的刚度为

(13)

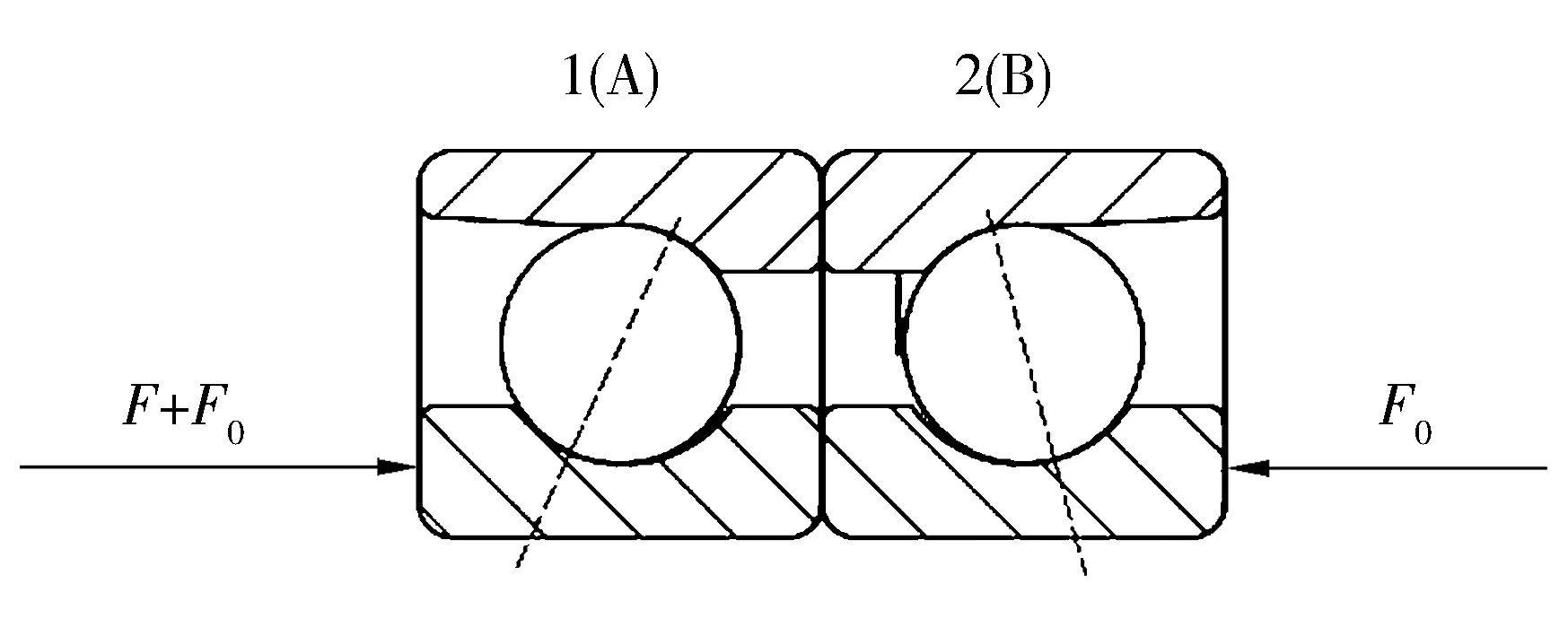
图3 DB组配型角接触球轴承加载示意图

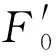
(14)

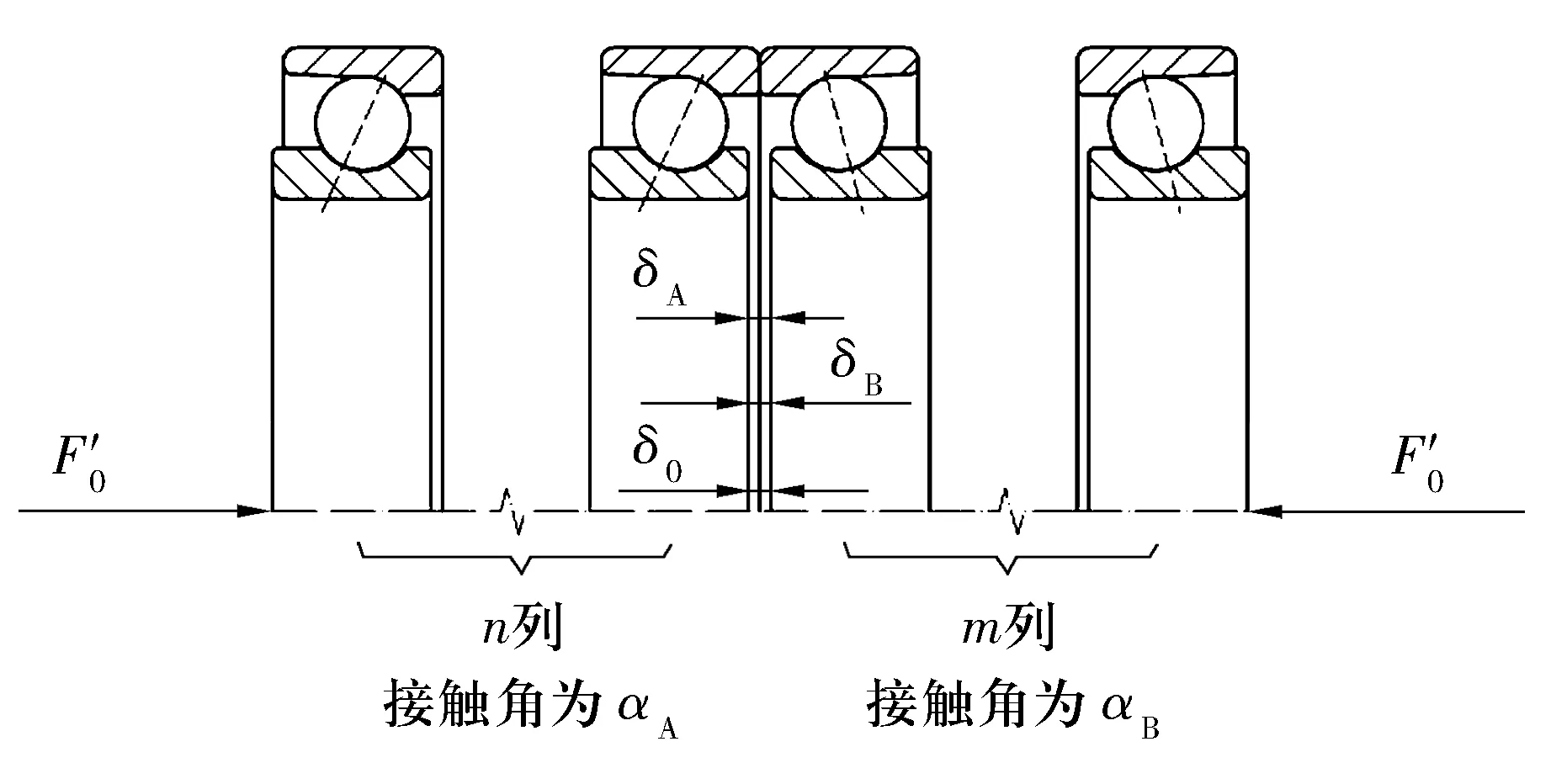
图4 多联角接触球轴承组配示意图

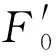
(15)

由图4可知

δA+δB=δ0，

(16)

联立(14)—(16)式可得

(17)

联立(8)，(9)，(14)，(15)，(17)式可得单套轴承的轴向位移为

(18)

(19)

令

(20)

(21)

则

δA=pδ0A，

(22)

δB=qδ0B。

(23)

KA=1.5knZ(sinαA)2.5(pδ0A)0.5=p0.5K0A=

(24)

KB=1.5knZ(sinαB)2.5(qδ0B)0.5=q0.5K0B。

(25)

故对于图4的多联组配角接触球轴承，其轴向刚度为

(26)

由(1)式可得接触角为αA的单套轴承所受预紧力为

(pδ0A)1.5=p1.5F0，

(27)

整个轴承组所需预紧力为

(28)

同理，接触角为αB的单套轴承所受预紧力为

FB=knZ(sinαB)2.5(qδ0B)1.5=q1.5F0，

(29)

同样可求得轴承组所需预紧力为

(30)

显然

np1.5=mq1.5。

(31)

通过上述计算可得不同组配方式下轴承所需的预紧力及轴向刚度，见表1(计算中忽略了接触角的变化，上述结果存在一定误差，为得到更准确结果，可在公式中输入实际接触角)。

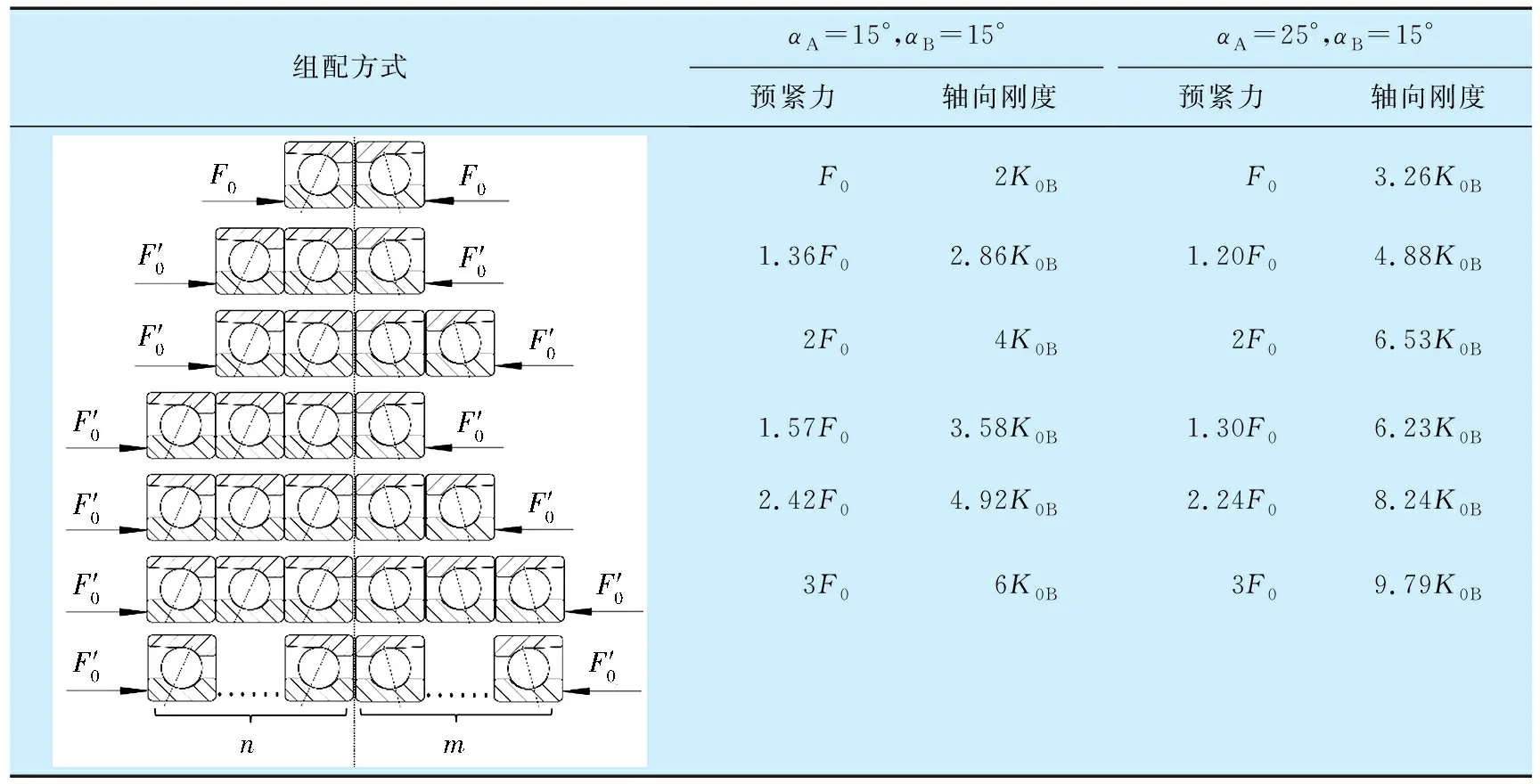
表1 角接触球轴承不同组配方式的刚度与预紧力

3 组配轴承径向刚度

某轴承厂家7005C和7005AC单列角接触球轴承的刚度与轴向力关系分别如图5和图6所示，由图可知：轴承刚度与轴向力呈非线性关系；轴向刚度随轴向力增大而增大，且在相同轴向力条件下，大接触角的轴承具有更高的轴向刚度；径向刚度与轴向刚度的比值与轴向力和接触角密切相关，接触角越小，刚度比值对轴向力的变化反映越明显。

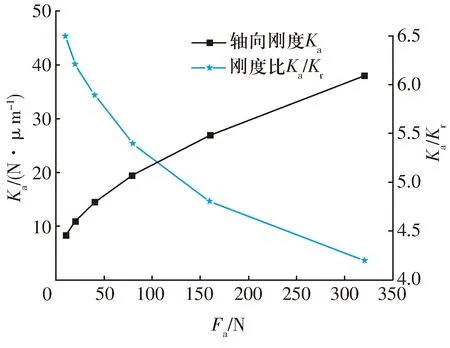
图5 7005C轴承刚度与轴向力关系

图6 7005AC轴承刚度与轴向力关系

轴向力与轴向刚度的关系可通过(4)式计算，但目前尚无简单有效的方法计算在特定预紧力(轴向力)下的径向刚度，只能查阅轴承厂家样本中轴向刚度和刚度比，进而计算轴承径向刚度。

对于两联组配轴承，预紧力F0作用下2列轴承的径向刚度分别为Kr1和Kr2，在受到径向力Fr时组配轴承产生径向位移δr(图7)，由此可得

Fr=Kr1δr+Kr2δr，

(32)

则两联组配轴承的径向刚度为

(33)

同理可求得m列轴承组配的径向刚度为

(Kr)m=Kr1+Kr2+…+Krm。

(34)

需要注意：轴承组配后预紧力发生变化，计算组配轴承径向刚度时，需根据轴承所受实际轴向力确定其轴向刚度与刚度比，进而得到各轴承及整个轴承组的径向刚度。

图7 两联组配轴承径向位移示意图

4 结束语

推导出组配角接触球轴承预紧力和刚度的计算通式，适用于具有相同和不同接触角的轴承，计算方法通用，大幅提高了组配轴承相关参数的计算效率。同时，列出了轴承在常用组配方式下的预紧力和轴向刚度，为轴承实际应用提供了参考。