汽车悬架推力球轴承组件冲击强度理论校核与台架试验
徐忠诚,孙国正,张文博,张健
(东风汽车集团股份有限公司 技术中心,武汉 430056)
1 概述
推力球轴承包含上下座圈、钢球以及保持架,钢球夹在2个座圈之间,2个座圈沿轴向平行、对齐布置,主要用于承受轴向载荷。汽车悬架用推力球轴承组件集成了悬架弹簧的上支承座、限位块固定支座等功能,这些功能通过座圈外面包裹的上下端盖实现(图1)。为满足集成功能、轻量化及设计空间的要求,上下端盖选用塑料并通过注塑成型,结构不规则,不同塑料材料的力学性能差异较大,很难用一套通用的公式或算法校验,故汽车悬架推力球轴承组件的强度设计要考虑轴承功能结构(金属部分)和集成功能结构(塑料部分)。

1—上端盖;2—上座圈;3—钢球;4—下座圈;5—保持架;6—限位块固定支座;7—下端盖
2 推力球轴承受力分析
推力球轴承受力极限工况有极限垂向冲击、侧向单边离地(临界侧翻),在强度设计时需取这2种工况中载荷较大者作为设计基准。
极限垂向冲击是指车轮受到地面最大垂向力冲击的工况,工程上一般在车辆满载条件下以3.5倍动载系数进行校核计算,即
(1)
式中:Gf为前桥满载;Fz1为垂向载荷。
车辆在行使过程中,由于纵向加速度(制动或加速)的作用会使前后桥轴荷转移,侧向加速度(转向或侧滑)的作用会使左右轴荷转移,将这2种影响叠到一起且出现单边离地时即出现除极限垂向冲击以外的最恶劣工况,前桥垂向载荷为
(2)
左、右轮载荷分别为
(3)
(4)
式中:G为整车满载载荷;L为轴距;b为车辆质心到后桥的距离;du/dt为纵向加速度;hg为车辆质心高度;ag为车辆纵向加速度;g为重力加速度;B为轮距。
按最恶劣工况进行强度校核,推力球轴承最大设计载荷为
Fa=max(Fz1,Fzfl,Fzfr)。
(5)
3 推力球轴承组件强度分析
推力球轴承组件包含推力轴承功能部分和集成功能结构部分,两者功能、材料各不相同,需分别进行强度分析。
3.1 轴承功能结构强度分析
除考虑球与沟道接触面上的最大接触应力外,还需考虑轴承零件自身的应力状态。
3.1.1 最大接触应力
球轴承的初始接触状态为点接触,如图2所示,接触体1为钢球,接触体2为套圈。已知接触体在接触点处的主曲率,可求得主曲率和以及主曲率函数,确定接触椭圆长、短半轴系数与接触变形系数,进而求出接触椭圆尺寸和接触应力[1-2]。
主曲率和为
∑ρ=ρ1Ⅰ+ρ1Ⅱ+ρ2Ⅰ+ρ2Ⅱ,
(6)
主曲率函数为
(7)
接触椭圆长、短半轴为
(8)
(9)
式中:ρ1Ⅰ,ρ1Ⅱ分别为钢球在主平面Ⅰ,Ⅱ内的曲率;ρ2Ⅰ,ρ2Ⅱ分别为套圈在主平面Ⅰ,Ⅱ内的曲率;u,v为长、短半轴系数,可参考文献[3]计算;Q为轴承所受载荷;E1,E2分别为钢球和套圈材料的弹性模量;ν1,ν2分别为钢球和套圈材料的泊松比。
定义椭圆率为
(10)
主曲率函数与e的关系为
(11)
(12)
(13)
式中:F,E分别为第一、二类完全椭圆积分;φ为椭圆幅度。
主曲率确定后,e值确定。长、短半轴系数u,v分别为
(14)
(15)
最大接触应力为
(16)
对于钢制轴承,E1=E2=206 GPa,ν1=ν2=0.3,(16)式可表示为[2]
(17)
ea=0.023 63u,
eb=0.023 63v。
对于推力轴承,钢球载荷为[3]
(18)
式中:Fa为轴承所受轴向载荷;Z为球数;α为压力角。
由(17),(18)式可得
(19)
对于球轴承,接触应力极限一般为4 200 MPa[4]。
3.1.2 最大切应力
在静止状态下,推力球轴承最大应力为钢球与沟道的接触应力,单向受压;但在实际工作过程中轴承内部存在多种接触状态,钢球与沟道的点接触状态为三向受压。除考虑压应力影响外,还要考虑切应力及其他方向上应力的影响,根据文献[5],接触中心点表面下 0.467b处的切应力最大。该点应力为
(20)
最大切应力为
(21)
对应等效应力
(22)
最大切应力状态下不会发生屈服的条件为
σr3<σRP-m0.2,
式中:σRP-m0.2为轴承钢屈服强度。
3.1.3 最大等效应力
根据文献[5],接触中心点的应力为
(23)
根据第四强度理论,等效应力为
,(24)
最大等效应力状态下不会发生屈服的条件为σr4<σRP-m0.2。
3.2 集成功能结构(塑料部分)冲击强度分析
推力球轴承集成功能结构主要是指集成了附加功能(弹簧上支座、前弹性限位块固定支座等)的上下塑料罩盖,结构不规则,强度设计、校核困难。鉴于此,提出以能量守恒定理为基础的设计、校核方法。
轴承功能结构部分为刚性,在受冲击时吸能较少,可忽略不计。下端盖受压变形量较小,吸收的能量有限,上端盖限位块固定支座在冲击过程中受限位块的挤压产生较大变形,吸收了绝大部分能量且为结构最薄弱部分,故塑料部分的强度校核重点为限位块固定支座处。
前桥冲击的能量传递路径为:轮边(包含轮胎)→减振器+弹簧→弹性限位块→推力轴承+前减上支承,则轮边冲击能量为
Ew=Ea+Es+Ed+Eth+Eto,
(25)
式中:Ea为减振器吸能;Es为弹簧吸能;Ed为限位块吸能;Eth为推力球轴承吸能;Eto为前减上支承吸能。
轮边冲击能量为
(26)
式中:Mw为轮边重量;v0为轮边初始冲击速度。
弹簧吸能为
(27)
式中:K为弹簧刚度;u1为轮边以最大速度向上冲击时弹簧的初始位置;u2为弹簧极限压缩位置。
减振器吸能为
(28)
式中:v(x)为减振器阻尼力-速度曲线函数;f(y)为减振器阻尼力-位移曲线函数;vf为轮边向上冲击至极限位置时的速度;l1为轮边以最大速度向上冲击时减振器初始位置;l2为减振器极限压缩位置。
限位块吸能为
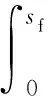
(29)
式中:K(s)为弹性限位块力-位移曲线函数;s为弹性限位块的位移;sf为弹性限位块达到压死高度时对应的位移。
前减上支承吸能为

(30)
式中:h(m)为前减上支承力-位移曲线函数;h1为轮边以最大速度向上冲击时前减上支承初始位置;h2为前减上支承极限压缩位置。
推力球轴承实际吸能为
Eth=Ew-Ea-Es-Ed-Eto。
(31)
单向拉伸或压缩时,应力σ和应变ε呈线性关系,利用应变能和外力做功在数值上相等的关系,应变能密度为[6]
(32)
则推力轴承上端盖发生塑性变形临界点时所吸收的能量为
(33)
式中:σRP0.2为端盖材料屈服强度;ε0.2为端盖发生屈服时的应变,一般取0.2%;A为上端盖限位块固定支座处平均截面面积;D为限位块固定支座中径。
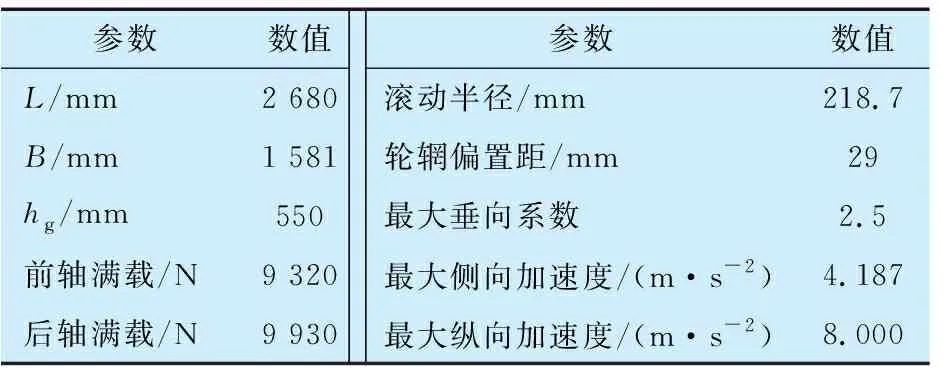
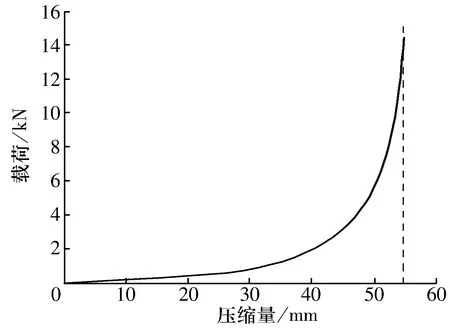
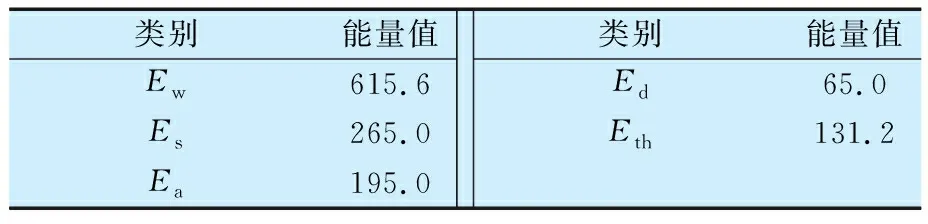
推力球轴承单次吸收的冲击能量不能高于上端盖发生塑性变形所需的能量,否则推力球轴承会出现早期失效甚至开裂,即Eth (34) 考虑到安全因素,设计时应将平均截面面积的下限值定义为最小截面要求,即最小截面面积为 (35) 功能结构和材料确定的情况下,推力球轴承塑料部分强度的校核或设计应以Amin作为主要考核项。 以某车型推力球轴承为例,对提出的计算方法方法进行验证,整车和轴承基本参数分别见表1、表2。该车型轮边质量为49.25 kg,最大冲击速度为5 m/s(路谱采集到的极限值,定义为初始冲击速度);弹簧刚度为18.9 N/mm,弹簧长度由159 mm压缩至96.7 mm(自由长度为349 mm)时减振器阻尼力曲线如图3所示,弹性限位块由零接触至压死状态的刚度曲线如图4所示。推力球轴承钢球及座圈材料均为GCr15轴承钢(均淬回火处理,无明显屈服,抗拉强度为1 800~2 400 MPa),端盖材料为PA66+GF30(屈服强度σRP0.2为165 MPa,抗拉强度σm为240 MPa,断裂延伸率为2.5%),上端盖限位块固定支座最小截面面积为1.643×10-4mm2,直径为60 mm。 表1 整车基本参数 表2 推力球轴承基本参数 图3 减振器阻尼曲线 图4 限位块刚度曲线 由第3.1节的计算方法可得pmax=3 183.1 MPa<4 200 MPa,σr3=1 699.1 MPa<1 800 MPa,σr4=1 396.1 MPa<1 800 MPa,说明轴承功能结构部分满足强度要求。根据3.2节的计算方法可得吸能情况见表3。 表3 冲击工况能量分布情况 上端盖发生塑性变形的临界能量点Etp=102 J,小于131.2 J,说明上端盖受到一次冲击会发生塑性变形,出现早期开裂或失效。 在该车型试验过程中推力球轴承上端盖出现开裂,金属部分无异常,如图5所示。更换轴承试验后短里程内仍出现开裂,表明推力球轴承的金属材料部分满足强度要求,塑料部分不满足,与校核结果一致。 图5 推力球轴承开裂裂口 根据整车开发流程,为保证产品的强度及可靠性,除进行强度计算外,还需对零部件进行强度试验,以验证设计方案的科学性、可靠性。由于推力轴承组件结构的特殊性,很难单独对其进行台架试验,一般都是搭载在整个前悬架系统上进行试验,然而前悬架系统台架上无法实现轮边的冲击条件(冲击速度达到5 m/s以上),不能对推力球轴承组件进行有效验证,且悬架系统台架试验成本高,周期长。鉴于此,提出一种强度试验方法:基于能量守恒定理将轮边对前悬架总成垂直向上的冲击转换为对推力球轴承的自由落体冲击。 首先,将限位块、推力球轴承、前减上支承装配好,倒置在试验台架上,台架上用专用工装对前减上支承进行定位、限位,如图6所示,限位块中间置有芯轴模拟减振器活塞杆,芯轴尾部设有台阶对限位块进行限位;然后,在推力球轴承组件正上方一定高度处放置质量块对其进行自由落体冲击。质量块系统包含质量块支承座和配重块,质量块支承座为均匀对称结构,通过4根同等规格的竖直立柱导向,高度可调。配置块根据试验规格放置在支承座上,试验时根据冲击能量和冲击速度的要求选择质量块和冲击高度。 1—质量块;2—四立柱;3—推力球轴承;4—固定工装 推力球轴承组件强度失效的主要表现形式是发生塑性变形或断裂,失效可能为多次超出屈服的冲击或一次性超抗拉的冲击所致,故试验内容应包含屈服临界点冲击和断裂临界点冲击。 5.2.1 屈服临界点冲击 为模拟真实工况,质量块配重以试验车型的轮边重量Mw为准,根据(33)式可求得推力球轴承上端盖的临界塑性变形能,在冲击能量确定的情况下试验高度hp为 (36) 5.2.2 断裂临界点冲击 质量块配重同5.2.1,推力球轴承临界断裂变形能为 (37) 式中:σm为端盖材料抗拉强度;εm为端盖材料断裂延伸率。 冲击高度hf为 (38) 5.2.3 试验方法 根据5.2.1,5.2.2中确定的重量和高度,选取相应的配置块,设置冲击高度。每种试验安排10组,每冲击一次检查推力球轴承组件是否开裂,记录冲击次数直至轴承组件开裂(若有环境件损坏或异常则需更换新件进行试验),然后更换新件进行下一组试验直至完成全部试验。 推力球轴承组件最大应力在超出屈服点时会发生塑性变形,随载荷的持续施加变形会越来越大直至零件开裂。由(33),(37)式可得推力球轴承组件断裂应变能与塑性应变能之比,即 (39) 对于工程塑料,断裂延伸率εm>2%,σm/σRP0.2>1.2,则N>12。即在5.2.1试验条件下,推力球轴承组件至少应能经受12次以上的冲击,而在5.2.2试验条件下允许出现一次性断裂。 通过对推力球轴承组件在整车上的受力分析,基于赫兹理论和能量守恒定律为推力球轴承组件强度的设计、校核提供一种较为简洁、高效的方法。通过对某车型推力球轴承组件冲击强度的计算,计算结果与整车试验结果高度吻合,验证了文中计算方法的有效性,并设计了一种推力球轴承强度试验的台架及方法,给出了接受标准。
4 实例计算



5 台架试验设计
5.1 方案设计

5.2 试验内容及方法
5.3 接受标准
6 结束语

