利用等价无穷小替换求极限时应注意的问题

黄 星，张倩瑶

(南阳职业学院，河南 南阳474500)

1 等价无穷小替换基本知识

知识1：无穷小的定义。如果当x→x0(或x→∞)时，函数f(x)的极限为零，则函数f(x)称为当x→x0(或x→∞)时的无穷小量，简称为无穷小。

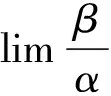
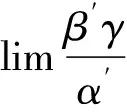
上述定理表明，当极限式为两个无穷小之比或无穷小是极限式中的乘积因子且替换后极限存在，则可使用等价无穷小替换求极限。

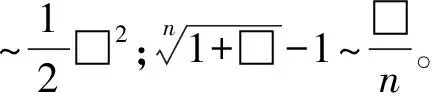
解法一(重要极限公式)：

解法二(洛必达法则)：

解法三(等价无穷小替换)：

解法一(洛必达法则)：

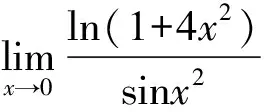
解法二(等价无穷小替换)：

2 利用等价无穷小替换求极限应注意的几个问题

例3：指出下列解法的错误之处。

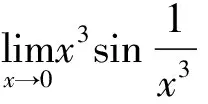
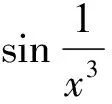
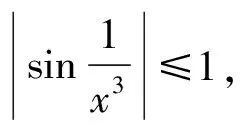
由例3可以看出，被替换的量在取极限时其极限必须为零，否则不能用等价无穷小替换。

例4：指出下列解法的错误之处。

解： ∵x→0时，sinx～x，tanx～x，

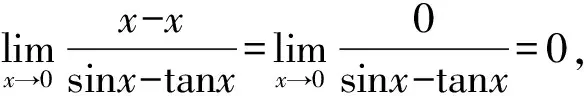
正确解法是：

由例4可以看出，被替换的量作为乘除因子时可以用等价无穷小替换，而作为加减因子时就会出错。事实上，等价无穷小替换在一定条件下对加减法也是成立的。等价无穷小替换对加减法成立的条件如下：

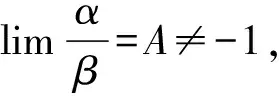
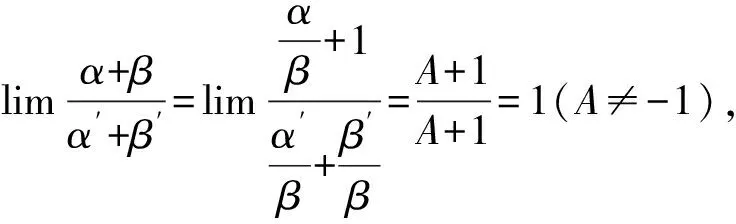
由等价无穷小替换对加减法成立的条件可知，不能直接用tanx-sinx去替换分子(etanx-1)-(esinx-1)，对于此题来说，等价无穷小替换对分子里的加减运算不适用，只能先将函数的分子恒等转化为乘除运算，然后再用等价无穷小替换。

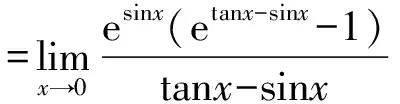
3 结语

在利用等价无穷小替换求极限时，要注意以下两点：①被替换的量在取极限时其极限必须为零。②对于分子分母中的乘积因子，可以放心使用等价无穷小替换。若分子或分母是两个等价无穷小之和或差，应慎用此种方法。