基于正负序分离的旋转变压器软件解码算法研究

郭志大，陈 磊，周 成，陈建明，刘 旺

（株洲中车时代电气股份有限公司， 湖南 株洲 412001）

0 引言

旋转变压器（简称“旋变”）具有坚固耐用、抗振动、适用温度范围广等优点，被广泛应用于新能源汽车的电驱动系统中。传统的旋变角度解码方式采用专用的硬件解码芯片（AD2S1210）或者软件解码提取旋变反馈信号的正余弦包络，然后将正余弦包络信号输入角度跟踪观测器中，利用角度观测器来解码出旋变的角度信息[1]。这种方式在旋变正余弦反馈信号异常情况下无法输出正确的角度信号[2]，解码输出的角度会引入相应的2倍频角度误差和直流偏置误差。2倍频的角度误差会引起电驱动系统的转矩高频振荡，严重影响驾驶感受，同时存在过流或IGBT模块损坏风险；而直流偏置误差会使电驱动系统的转矩控制误差增大、电驱动系统偏离最佳的工作曲线。本文中旋变反馈信号异常均指正余弦包络信号幅值不平衡或者相位不正交或者两种情况兼有。文献[2]仅针对旋变信号的幅值异常进行了研究，幅值异常补偿是通过对d轴分量与角度的微分进行的，微分操作容易引入高频噪声，因此工程实际应用价值不大。文献[3-6]研究了电网不平衡条件下的锁相环设计，与旋变信号反馈异常有类似之处，但同样没有考虑相位不正交的情况。国内外对旋变反馈信号异常下的解码研究很少，相关文献不多。基于此，根据不平衡电网的正负序锁相环设计方法，本文提出了一种基于正负序分离的旋变软件解码算法，其能够在旋变反馈信号异常情况下解码出正确的角度信号，极大地提高了旋变反馈信号异常情况下的解码精度。

1 旋变解码角度误差分析

旋变正余弦包络信号对旋变解码至关重要，将直接影响解码输出的角度。本节重点分析旋变信号异常对输出角度的影响。

1.1 旋变解码原理

为了得到平滑的角度信息，一般由角度跟踪观测器对旋变反馈的正余弦包络信号进行跟踪处理，得到旋变的角度信息和速度信息。角度跟踪观测器原理如图1所示[7]，其中，ω为旋变速度，跟踪角度误差计算公式如下：

式中：ε——跟踪角度误差；θ——旋变角度；——观测器输出角度。

将旋变反馈的正余弦包络信号放到两相静止坐标（αβ坐标）中，余弦包络对应α轴，正弦包络对应β轴，则正余弦反馈信号在αβ坐标下的空间矢量为圆形的旋转矢量，即Vs=cosθ+jsinθ=ejθ。

利用两相静止坐标到dq旋转坐标的变换公式，见式(2)，发现角度误差实际上等于旋转矢量Vs在dq旋转坐标下的q轴分量，即ε=Uq。角度跟踪观测器的工作过程可以被理解为通过不断地调整自身角度输出来跟踪旋转矢量Vs。当两者频率和相位一致时，旋转矢量在q轴的分量为0，此时角度误差也为零，即ε=0。

1.2 幅值异常下的角度误差分析

不失一般性，以旋变余弦信号幅值做参考，假定其幅值基准为1，幅值异常情况下的旋变正弦信号幅值用“1+Δ”表示，Δ表示相对于基准幅值的偏差百分比。比如，Δ=-0.3表示正弦幅值小于基准幅值30%，即正弦幅值为余弦幅值的70%。如此，正余弦信号在αβ坐标下的空间旋转矢量为

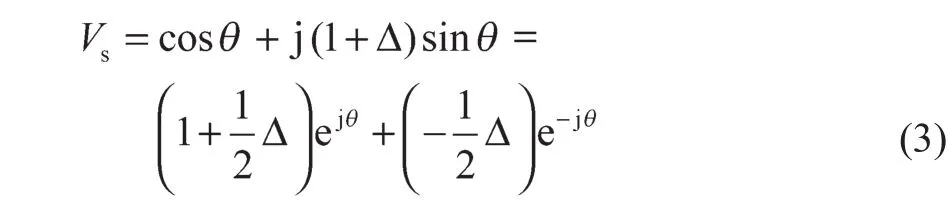
为了使解码角度正确，角度跟踪观测器应该对正序的θ角进行跟踪。当角度跟踪观测器输出角度跟踪至正序θ角时，旋转矢量Vs中的正序和负序分量在正负序dq坐标下的表达式为

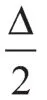
1.3 相位异常下的角度误差分析

以余弦信号作为参考，正弦信号的相位与余弦信号的相位不正交，存在相位正交误差δ，则正余弦信号的空间旋转矢量为

对式(5)进行欧拉公式转换，可得

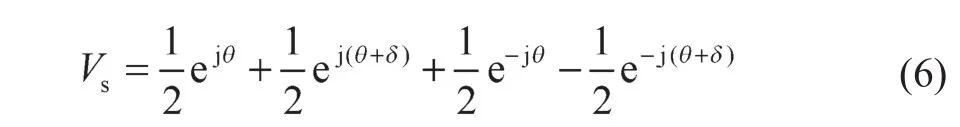
角度跟踪观测器旋转至θ角时，旋转矢量Vs中的正序分量和负序分量在正负序dq坐标下的表达式为

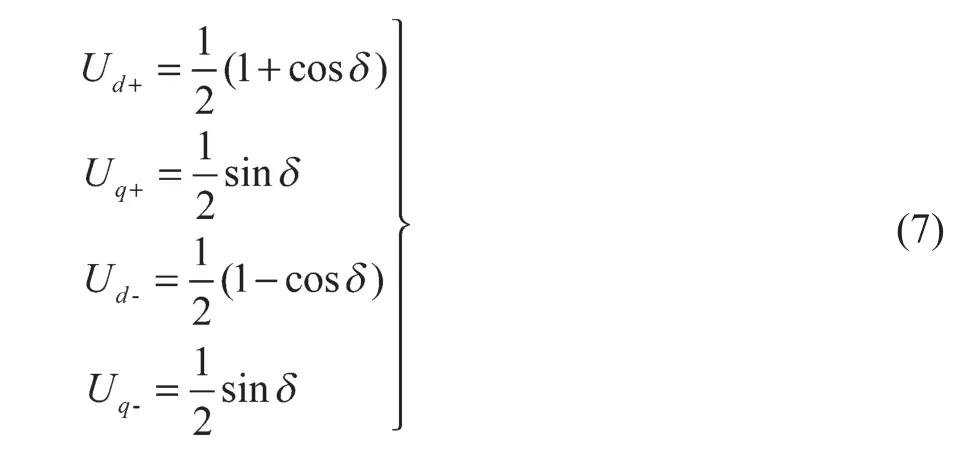
图2 正序分量的合成矢量Fig. 2 Resultant vector of positive sequence components

1.4 幅值和相位均异常下的角度误差分析

以余弦信号作为参考，正弦信号与余弦信号的幅值存在Δ差异，同时存在相位正交误差δ，则正余弦信号的空间旋转矢量为

对式(8)进行欧拉公式转换，可得

根据式(9)可以发现，当相位正交误差δ为零时，式(9)可以转换为式(3)；当幅值误差Δ为零时，式(9)可以转换为式(6)。这表明前面两种误差情形均为本次误差情形的一种特例。

角度跟踪观测器旋转至θ角时，旋转矢量Vs中的正序分量和负序分量在正负序dq坐标下的表达式为

由正负序分量可知，幅值和相位均异常的情况下，不仅存在直流分量误差，还存在2倍频的交流分量误差。

2 正负序分离的解码算法设计

根据前面的分析可知，当相位出现不正交误差时，正序分量Uq+就不为零，由此导致角度跟踪观测器输出角度中存在直流分量误差。通过式(4)～式(10)可以发现，始终存在Uq+=Uq-，正好可以利用负序分量Uq-来消除角度跟踪观测器中的直流分量误差。当旋变信号异常时，会产生负序分量。正是由于负序分量的存在，负序分量在正序坐标q轴下表现为2倍频波动，导致输出角度出现2倍频波动。为了消除正序坐标q轴下的2倍频波动误差，将负序分量进行2倍频负序逆变换，得到正序坐标下q轴的2倍频波动信号，两者相减即可去除正序坐标q轴的2倍频波动误差。基于以上原理，设计了正负序分离的角度跟踪观测算法，其原理如图3所示。

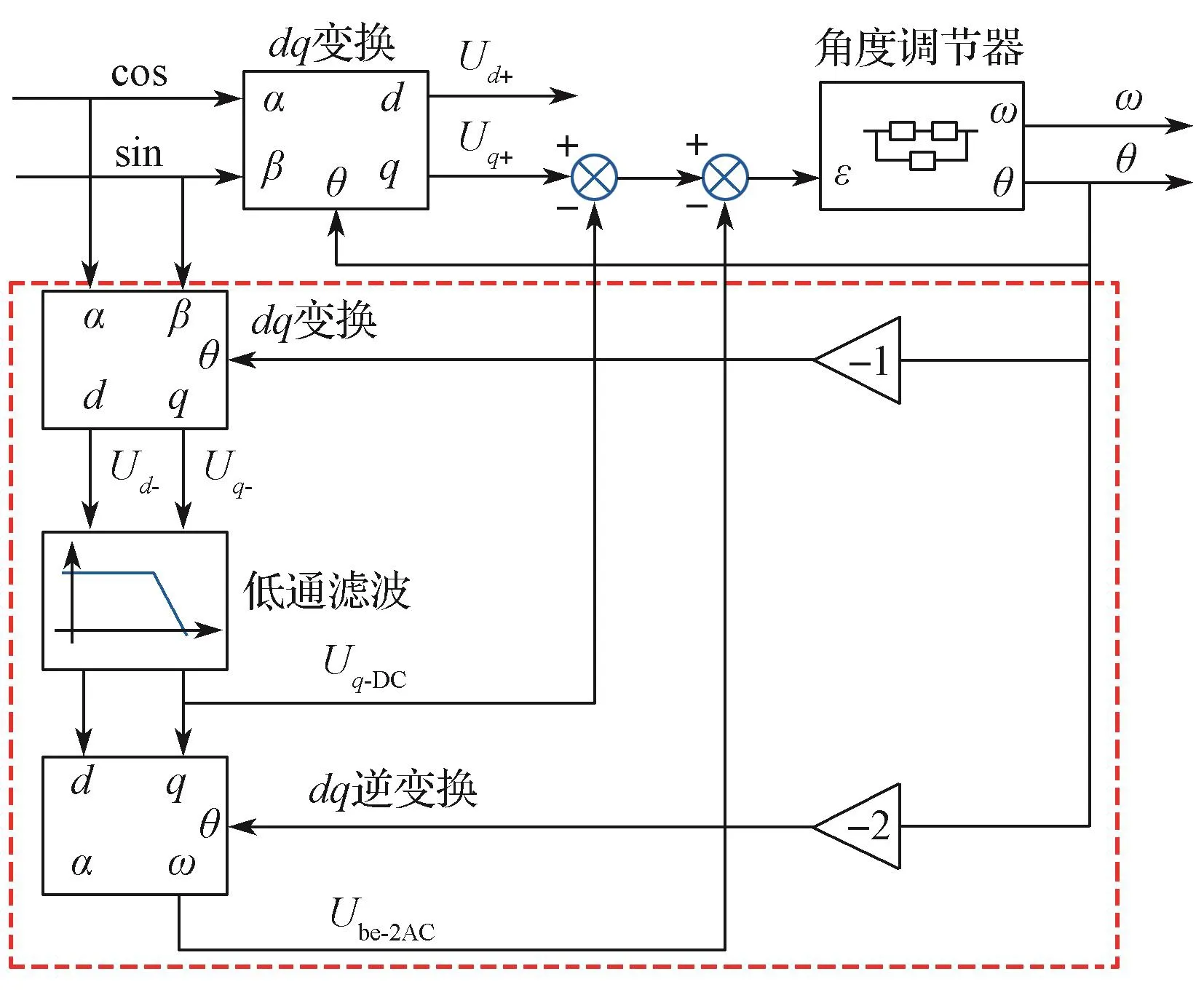
图3 正负序分离的旋变解码算法框图Fig. 3 Block diagram of the resolver decoding algorithm based on positive and negative sequence separation

正负序分离的旋变解码算法是在正常的旋变解码算法基础上加入了负序补偿算法。图3中，虚线框中部分即为负序补偿算法。负序补偿算法首先对旋变正余弦反馈信号做负序dq变换，负序分量在负序dq变换后表现为直流量；同时负序dq变换也会将正序分量变换为2倍频率的交流量。为了得到负序分量的直流量，引入了低通滤波器。通过低通滤波器后，可得到式(10)中的Ud-与Uq-信息。图3中的直流补偿量Uq-DC即为Uq-，用于补偿由于相位不正交引入的直流分量误差Uq+。负序分量的直流信息再通过2倍频负序逆变换得到交流补偿量Ube-2AC。根据正负序dq变换可知，Ube-2AC为负序分量在正序变换中的2倍频波动量，因此可以利用Ube-2AC来去除正常解码过程中因负序分量存在引入的2倍频波动误差。

3 仿真与实验

为了验证本文所提算法的可行性，首先建立了Matlab/Simulink仿真模型，通过仿真对其原理进行验证；其次编写了相应的控制算法，并将算法移植到电驱系统中，开展相应的硬件在环测试（hardwarein-the-loop, HIL），以验证算法的实际效果。

3.1 仿真验证

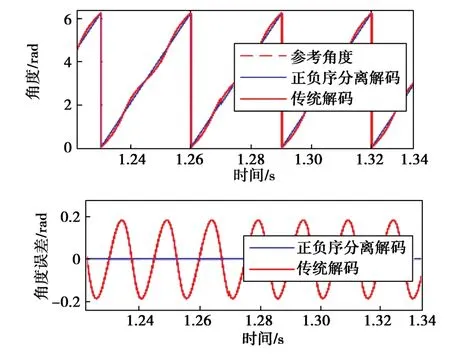
图4 幅值异常下传统解码算法与正负序分离解码算法角度输出仿真(Δ=-0.3 )Fig. 4 Simulation of traditional decoding algorithm and positive - negative sequence separation decoding algorithm under abnormal amplitude (Δ=-0.3 )

图5 相位异常下传统解码算法与正负序分离解码算法角度输出仿真( δ=15°)Fig. 5 Simulation of traditional decoding algorithm and positive - negative sequence separation decoding algorithm under abnormal phase (δ=15° )

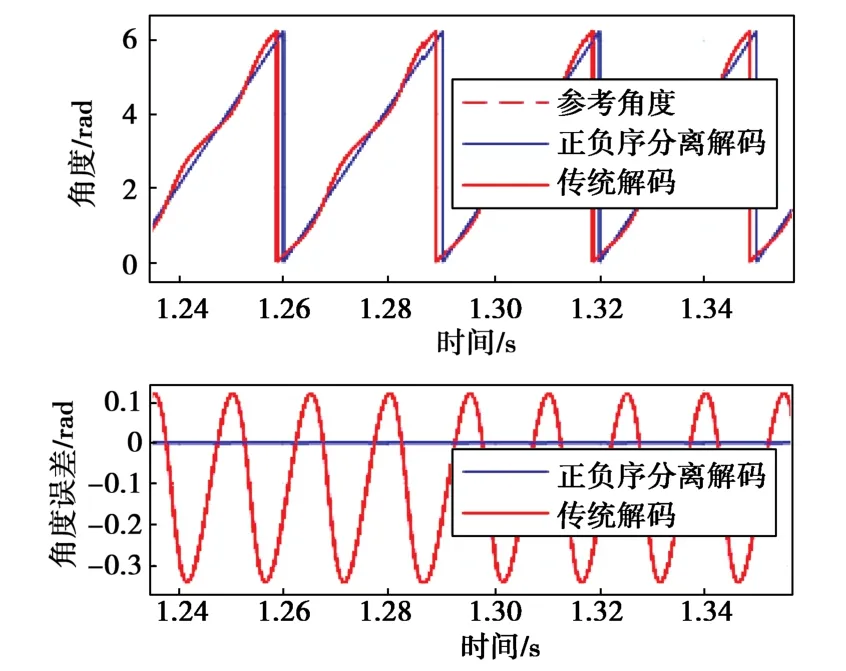
图6 幅值和相位均异常下传统解码算法与正负序分离解码算法角度输出仿真 (Δ=-0.3, δ=15° )Fig. 6 Simulation of traditional decoding algorithm and positive-negative sequence separation decoding algorithm under amplitude imbalance and abnormal phase (Δ=-0.3, δ=15°)

3.2 实验验证

为了验证本文所提算法的实用性，在dsPACE的HIL实验平台上进行测试。通过设置dsPACE中的旋变信号幅值偏差以及相位误差来模拟旋变信号异常情况。图7～图9示出旋变转速为500 r/min工况下的测试波形（旋变极对数为4），测试过程中在0.05 s时刻之前为正常的旋变解码算法，0.05 s时刻之后使能了本文所提的正负序分离的解码算法。图7～图9中，sin为旋变正弦反馈信号，cos为旋变余弦反馈信号，angle为解码算法输出的旋变角度信号。可以看出，实验波形与仿真波形高度一致，表明正负序分离的旋变解码算法能够在幅值和相位异常情况下解码出正确的角度信息，极大地提高了解码精度。

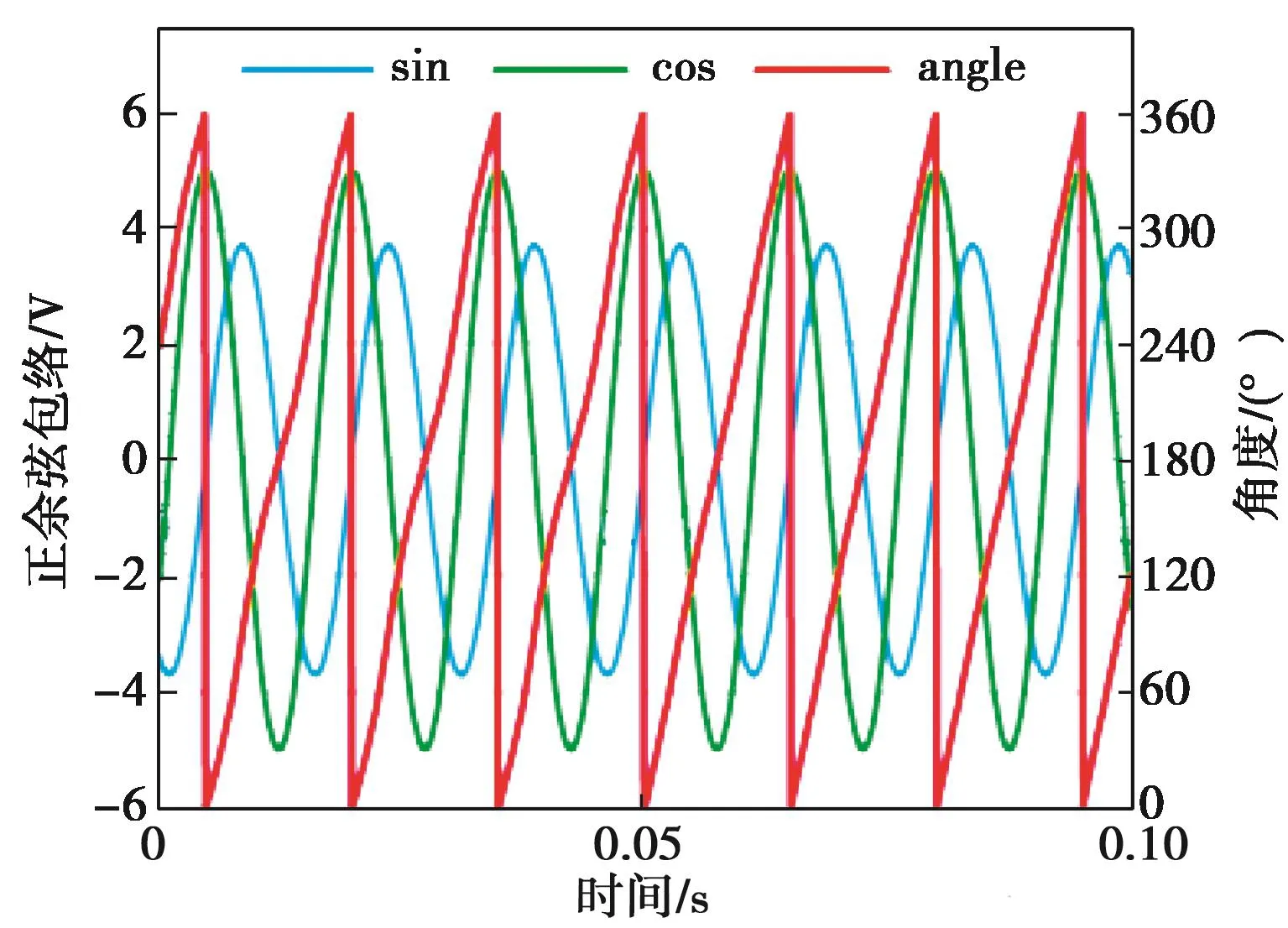
图7 幅值异常下旋变解码角度实验波形(Δ=-0.3)Fig. 7 Experimental decoding angle waveforms of resolver under amplitude imbalance (Δ=-0.3)

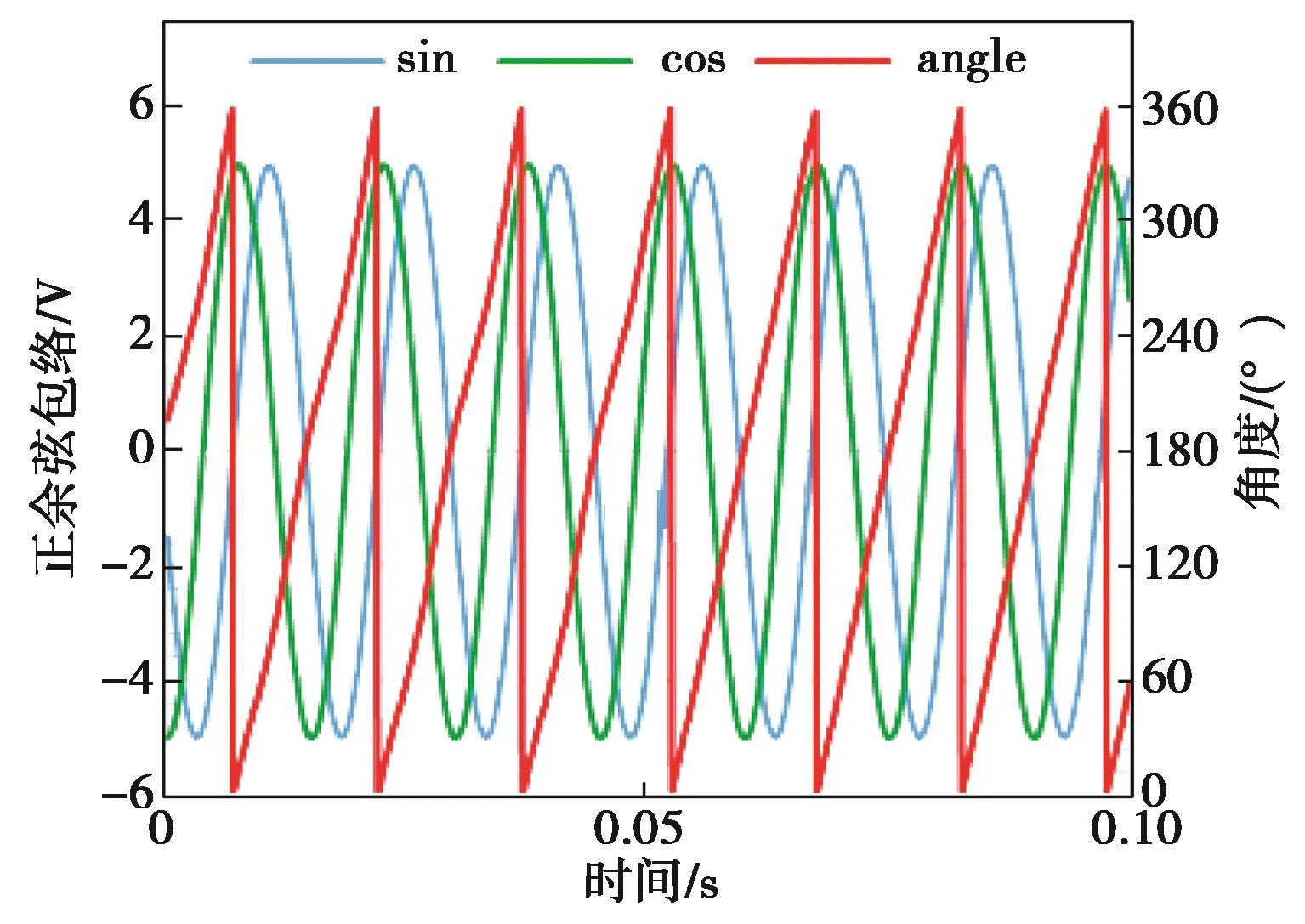
图8 相位异常下旋变解码角度实验波形(δ=15°)Fig. 8 Experimental decoding angle waveforms of resolver under phase non-orthogonality (δ=15°)

图9 幅值和相位异常下旋变解码角度实验波形(Δ=-0.3, δ=15°)Fig. 9 Experimental decoding angle waveforms of resolver under amplitude imbalance and phase non-orthogonality(Δ=-0.3, δ=15°)

4 结语

本文对旋变正余弦反馈信号异常情况（幅值不平衡、相位不正交）的正负序分量进行了分解，分析了正负序分量对解码角度的影响：由于负序分量的存在，旋变解码角度出现2倍频的误差波动；由于相位不正交误差的存在，解码输出的角度中不仅含有2倍频的波动误差，还存在直流分量误差。在此基础上，文章提出了一种基于正负序分离的旋变解码算法，利用所提取的负序分量来消除正序分量中的干扰部分。仿真及实验测试结果表明，该解码算法在旋变信号异常情况下具有较高的解码精度，能够有效地去除输出角度中的2倍频波动误差和直流分量误差，具有较高的工程应用价值，极大地拓展了旋变的正常工作范围，降低了系统对旋变解码电路的要求。

目前，旋变信号的负序分量提取是通过低通滤波器来完成的，其在低速下的提取效果不理想，如何快速有效地提取负序分量将是下一步研究的重点。