机车动力蓄电池充电机用三电平Buck变换器建模及其控制系统设计

杜 超，郭 维，曾明高，丁磊磊，李炳璋，李 昊

（株洲中车时代软件技术有限公司，湖南 株洲 412001）

0 引言

与两电平Buck变换器相比，三电平Buck变换器有诸多优点，如输入开关管与续流二极管的电压应力只有输入电压的一半；在输入输出条件相同的情况下，输出滤波电感可以减小至原来的四分之一；输出滤波电容可以减小至原来的一半[1-2]。然而三电平Buck变换器本质上是一个时变、非线性电路，随着开关状态的切换，电路的拓扑会发生改变，使得对其分析与设计比较困难[3]。文献[4-5]介绍了一种基于电压单闭环的控制方法，其实现简单但存在暂态响应速度慢、抗扰性差等缺点。文献[6]提出了一种基于扰动观测器的电压控制策略，其缩短了电压环暂态响应时间，提高了抗外部扰动能力，但是仍然存在电感电流不受控制的问题，不适用于输出接蓄电池的场景。为此，本文提出了一种适用于输出接蓄电池的三电平Buck变换器的控制系统设计方案，在分析各个开关模态下电路的工作过程的基础上，基于状态空间平均法[1]建立了其简化线性模型，并设计了输出电压、输出电流、分压电容电压三闭环控制系统。仿真结果表明，采用该方案设计的动力蓄电池用三电平Buck变换器输出电流动态响应快，抗输入电压波动能力强，可以满足工程实际应用。

1 主电路介绍

动力蓄电池充电机用三电平Buck变换器的主电路拓扑如图1所示。其中，C1和C2是分压电容器，其容值足够大且C1=C2；Ud为电容均分输入电压；R1，R2为均压电阻器；功率开关器件VT1和VT4交错工作，其驱动信号相位相差180°[7-8]；VT2和VT3始终处于关断状态，仅做续流二极管用；L是输出滤波电感器且电感量足够大，电感器输出端与蓄电池相连；r1是L内阻。

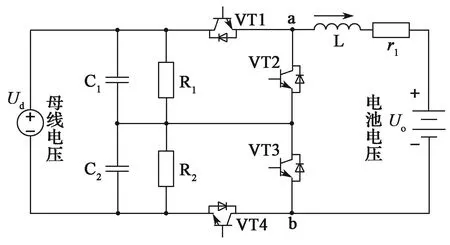
图 1 三电平Buck变换器主电路Fig. 1 Main circuit of three-level Buck converter

2 数学模型及等效电路推导

三电平Buck变换器有占空比d≥0.5和d＜0.5两种模式[9]。本节详细分析了三电平Buck变换器的工作原理，并推导出其线性等效电路。

2.1 d≥0.5情况

图2示出电感电流连续情况下d≥0.5时变换器的主要波形。在一个开关周期Ts内，存在VT1和VT4同时导通、VT1导通VT4关断、VT4导通VT1关断3种工况。

图 2 d≥0.5时三电平Buck变换器的主要波形Fig. 2 Main waveforms of three-level Buck converter as d≥0.5

2.1.1t0～t1阶段

在t0～t1阶段，VT1和VT4同时导通，变换器等效电路如图3所示。

图 3 VT1和VT4同时导通时变换器等效电路Fig. 3 Equivalent circuit of the converter as VT1 and VT4 conducting at the same time

电流从直流母线正端开始，经VT1、电感L、电池和VT4后形成回路。该阶段，C1和C2的电压uC1和uC2保持不变，电容器内无电流流过。输入电压Ud与输出电压Uo的压差作用在L上，电感电流线性上升。该阶段持续时间为(d-0.5)Ts。以＜x＞表示状态x在一个开关周期的平均值，变换器满足低频和小纹波工况假设，可以近似认为状态变量与输入变量在一个开关周期内基本保持不变，并用开关周期平均值进行近似[1]。于是有

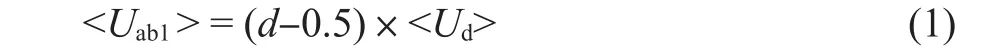
式中：＜Uab1＞——在t0～t1阶段，a, b点间电压在一个开关周期的平均值；＜Ud＞——输入电压开关周期平均值。

2.1.2t1～t2阶段

在t1～t2阶段，VT1开通，VT4关断，变换器等效电路如图4所示。电流从直流母线正端开始，经VT1、电感L、电池、VT3、电容器C1和C2后形成回路。该阶段C1放电，电压下降；C2充电，电压上升；流经电容器的电流大小为电感电流的一半。uC1与Uo的压差作用在L上，由于uC1＜Uo，电感电流线性下降。该阶段持续时间为(1-d)Ts。

图 4 VT1导通、VT4关断时变换器等效电路Fig. 4 Equivalent circuit of the converter as VT1 turn on and VT4 turn off

在该阶段，有

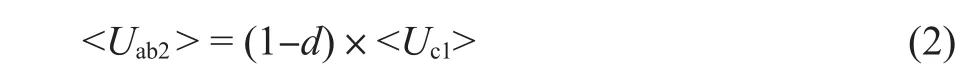
式中：＜Uab2＞——在t1～t2阶段，a, b点间电压在一个开关周期的平均值；＜Uc1＞ —— C1电压开关周期平均值。

2.1.3t2～t3阶段

在t2～t3阶段，VT1和VT4同时开通。该阶段持续时间为(d-0.5)Ts，电路工作情况与t0～t1阶段的相同。在该阶段，有

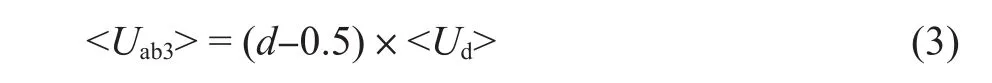
式中：＜Uab3＞ ——在t2～t3阶段，a, b点间电压在一个开关周期的平均值。

2.1.4t3～t4阶段

在t3～t4阶段，VT1关断，VT4开通，变换器等效电路如图5所示。

图 5 VT1关断，VT4导通时变换器等效电路Fig. 5 Equivalent circuit of the converter with VT1 turn off and VT4 turn on

电流从母线电压正端开始，经C1、VT2的续流二极管、L、电池、VT4及C2后形成回路。该阶段C2放电，电压下降，C1充电，电压上升，流经电容器的电流大小为电感电流的一半。uC2与Uo的压差作用在L上，由于uC2＜Uo，电感电流线性下降。该阶段持续时间为(1-d)Ts。在该阶段，有

式中：＜Uab4＞ ——在t3～t4阶段，a, b点间电压在一个开关周期的平均值；＜Uc2＞ —— C2电压开关周期平均值。

由式(1)～式(4)可以得到在一个开关周期内a, b点间电压的平均值：

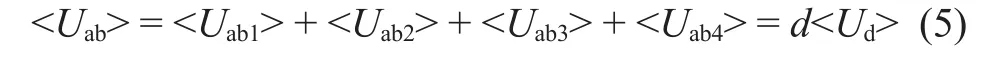
2.2 d＜0.5情况

图6示出电感电流连续情况下d＜0.5时变换器的主要波形。在一个开关周期，存在VT1和VT4同时关断、VT1导通VT4关断、VT4导通VT1关断3种工况。

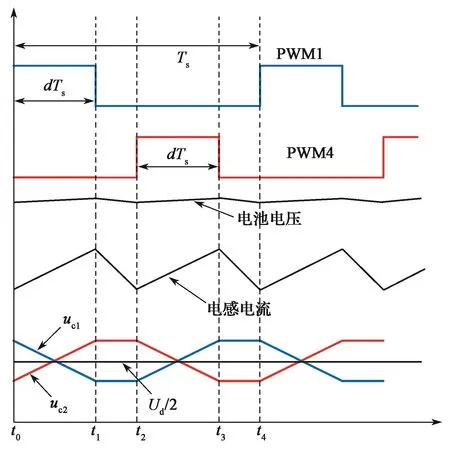
图 6 d＜0.5时变换器的主要波形Fig. 6 Main waveforms of the converter as d＜0.5

2.2.1t0～t1阶段

在t0～t1阶段，VT1开通、VT4关断，变换器等效电路如图4所示。该阶段C1放电，电压下降；C2充电，电压上升；电容电流大小为电感电流的一半。uC1与Uo的压差作用在L上，由于uC1＞Uo，电感电流线性上升。该阶段持续时间为dTs。在该阶段，有

2.2.2t1～t2阶段

在t1～t2阶段，VT1和VT4同时关断，变换器等效电路如图7所示，该阶段持续时间为(0.5-d)Ts，电感电流通过VT2和VT3续流二极管续流；分压电容内无电流流过，电容电压保持不变。在该阶段，a, b点之间的电压开关周期平均值为

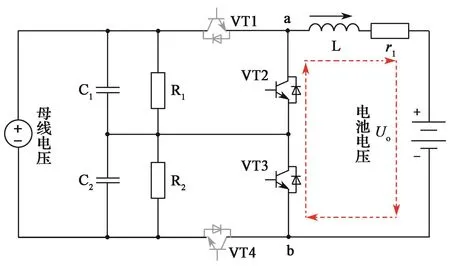
图 7 VT1 和VT4 同时关断时变换器等效电路Fig. 7 Equivalent circuit of the converter as VT1 and VT4 turn off at the same time

2.2.3t2～t3阶段

在t2～t3阶段，VT1关断、VT4导通，变换器等效电路如图5所示。该阶段C1充电，电压上升；C2放电，电压下降；流经电容的电流大小为电感电流一半。uC2与Uo的压差作用在L上，由于uC2＞Uo，电感电流线性上升。该阶段持续时间为dTs。在该阶段，有

2.2.4t3～t4阶段

t3～t4阶段，VT1和VT4同时关断，该阶段持续时间为(0.5-d)Ts，工作过程与t1～t2阶段类似。在该阶段，有

由式(6)～式(9)可以得到在一个开关周期内ab两点间电压的平均值为

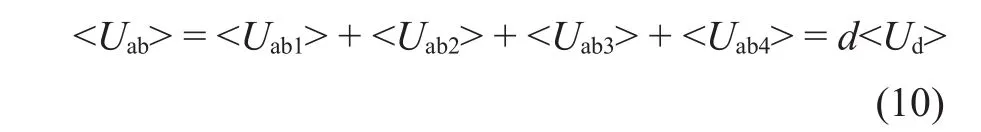
由式(5)和式(10)可以看出，对于d≥0.5与d＜0.5两种工作模式，三电平Buck变换器a, b点间电压的开关周期平均值表达式相同，因此，可以用同一等效电路。

2.3 线性等效电路

将电池简化等效成一个大电容（C）串联一个小内阻（r2）形式，将a, b点间的电压用开关周期平均值d＜Ud＞代替，可以得到三电平Buck变换器的简化等效电路（图8）。由于该电路是一个线性电路，因此控制系统的设计得以大大简化。

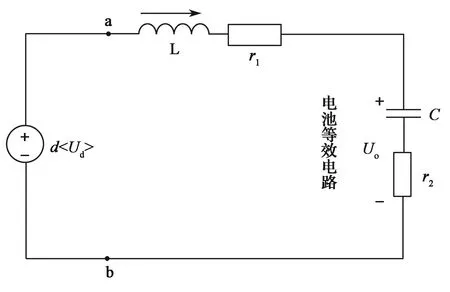
图 8 三电平Buck变换器线性等效电路Fig. 8 Equivalent linear circuit of three-level Buck converter

根据基尔霍夫电压定律、基尔霍夫电流定律、欧姆定律，由等效电路（图8）可以得到从占空比到电感电流的传递函数为

从电感电流到输出电压的传递函数为

3 闭环控制系统设计

动力电池充电电流指令值由蓄电池自带的管理系统给出，DC/DC变换器按照该指令输出，因此动力电池的充电电压、电流均需要受控，故本文采用电压、电流、均压三环控制方式，并对电流环、电压环进行了设计。

3.1 电流环设计

用Gid表示从占空比到电感电流的传递函数，式(11)可以写为

电流环采用PI控制，其原理如图9所示。

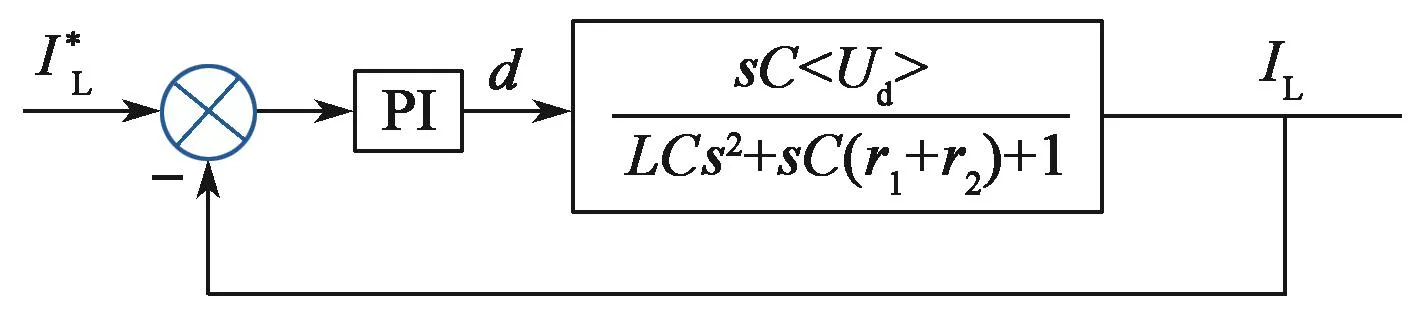
图 9 电流环控制框图Fig. 9 Block diagram of current loop control

从图9得到电流环开环传递函数为

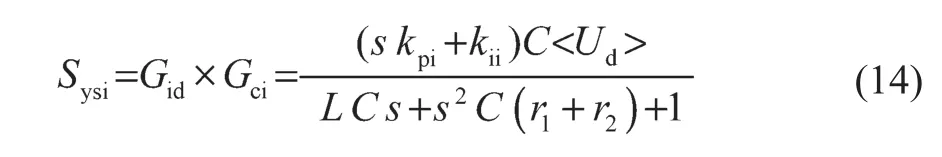
式中：Gci——电流环PI控制器传递函数；kpi——电流环比例系数；kii——电流环积分系数。

取Ud=1 500 V，L=4 mH，C=300 F，r1=20 mΩ，r2=50 mΩ，kpi=0.006 683，kii=1.179 732，得到电流环的开环波特图，如图10所示。可以看出，系统低频增益高，在401 Hz处以-20 dB/dec穿越零分贝线，相角裕度约为85°。电流环动态响应快，超调小，可以满足工程要求。

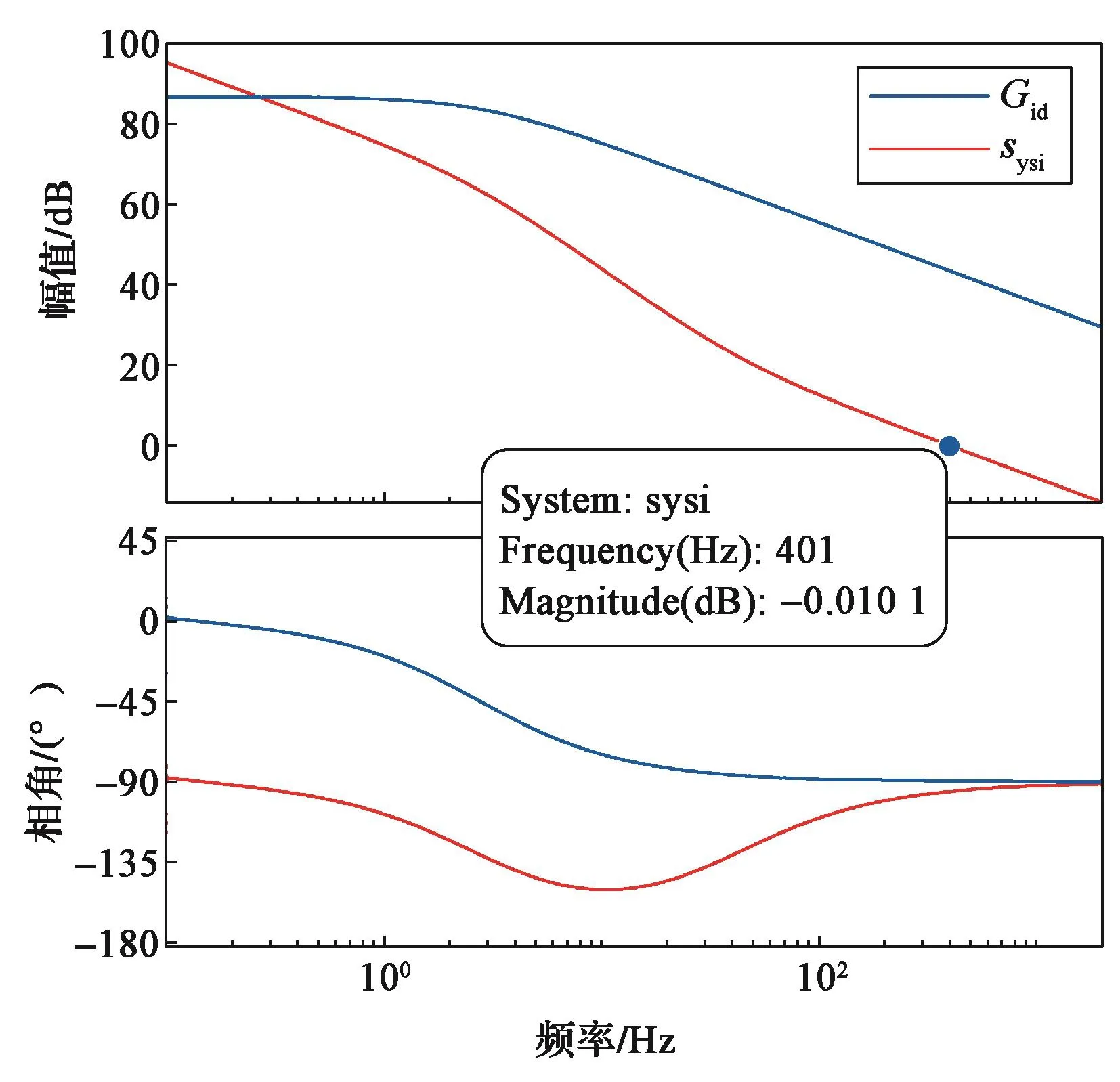
图 10 电流环开环波特图Fig. 10 Open loop Bode diagram of current loop

3.2 电压环设计

式(12)给出了从电感电流到输出电压的传递函数。实际应用中，当电流环带宽远大于电压环带宽时，电流环可以迅速响应电压环输出指令，因此可将电流内环近似成一个一阶低通滤波器，从而简化电压环设计。

电压环采用PI控制，电压环输出作为电流环的给定，可得电压环的控制框图，如图11所示，其中Ti为电流环近似等效后的滤波时间常数。

图11 电压环控制框图Fig. 11 Block diagram of voltage loop control

令kpu为电压环比例系数，kiu为电压环积分系数，可以得到电压环的开环传递函数：

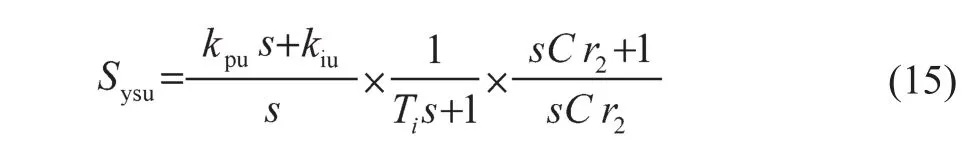
取kpu=2.018 366，kiu=5.072 708×103，得到电压环的开环波特图（图12）。可以看出，系统在40.6 Hz处以-20 dB/dec穿越零分贝线，相角裕度约为90°。

图 12 电压环开环波特图Fig. 12 Open loop Bode diagram of voltage loop

3.3 分压电容均压控制[10]

从上述分析可知，流过分压电容器的电流大小相等、方向相反。因此，当VT1和VT4的占空比不相等时，一个开关周期内分压电容的充放电时间不相等，分压电容器之间会出现压差。如果不加以调节控制，压差会越来越大，最终导致系统失效。

图13示出均压环的控制框图，对分压电容器压差进行比例控制，将补偿占空比Δd适当限幅后叠加到电流环输出，以修正开关管的占空比。

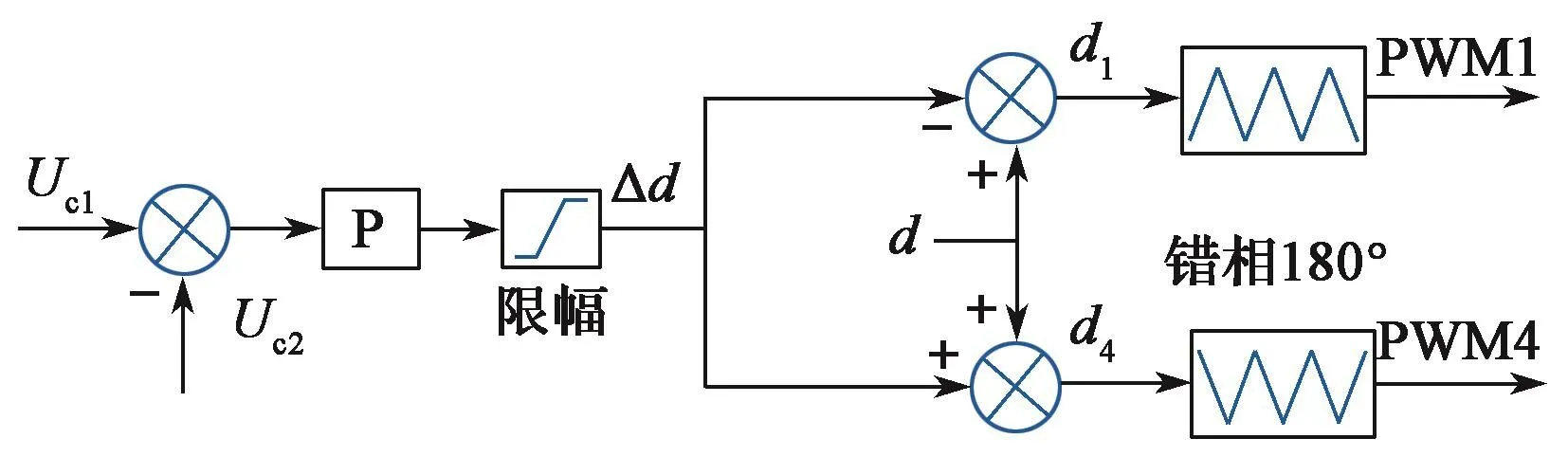
图13 均压环控制框图Fig. 13 Block diagram of equalizing loop control

若Uc1电压高于Uc2，则增大VT1的占空比，同时减小VT4的占空比；反之，则减小VT1的占空比，同时增大VT4的占空比。

3.4 闭环控制策略

本文所讨论的控制策略主要针对给机车动力蓄电池充电的场景，需要对充电电流加以控制，因此选择“电压—电感—均匀三闭环”控制策略，具体如图14所示。

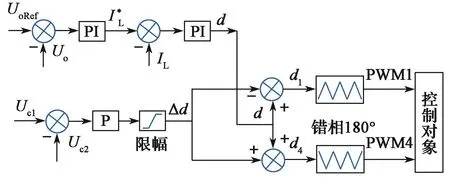
图14 三电平Buck三闭环控制框图Fig. 14 Block diagram of the three-level Buck three-closedloop control

3.4.1 电压控制

系统根据动力蓄电池的温度补偿曲线和蓄电池温度得到输出电压的给定值；以滤波后蓄电池电压值作为电压环的反馈值，将给定值与反馈值进行比较得到偏差电压，经过PI控制后以电压环的输出作为电流环的给定值，并将给定值限幅设置为动力蓄电池的最大允许充电电流。

3.4.2 电感电流控制

电感电流经低通滤波后作为电流环的反馈值；将电流给定值与反馈值比较得到偏差电流，再经过PI控制后，可以得到占空比d。

3.4.3 均匀三闭环控制

检测分压电容器电压Uc1与Uc2的偏差，计算出补偿占空比Δd。将(d+Δd)作为VT1的占空比、(d-Δd)作为VT4的占空比送入PWM模块后，生成相应的脉冲，该脉冲信号经驱动电路后被加在相应的开关管上，从而实现对输出电压、电感电流、分压电容压差的三闭环控制。

4 仿真分析

为了验证简化等效模型（图8）及控制参数设计的正确性，在Matlab/Simulink环境中搭建了一个220 kW的动力蓄电池充电机主电路模型。考虑实际运用情况，分别进行了分压电容均压控制、网压跳变、中间直流电压波动、限流转恒压充电等模拟实验，主电路仿真参数如表1所示。其中，均压环采取比例控制，比例系数取5×10-4。

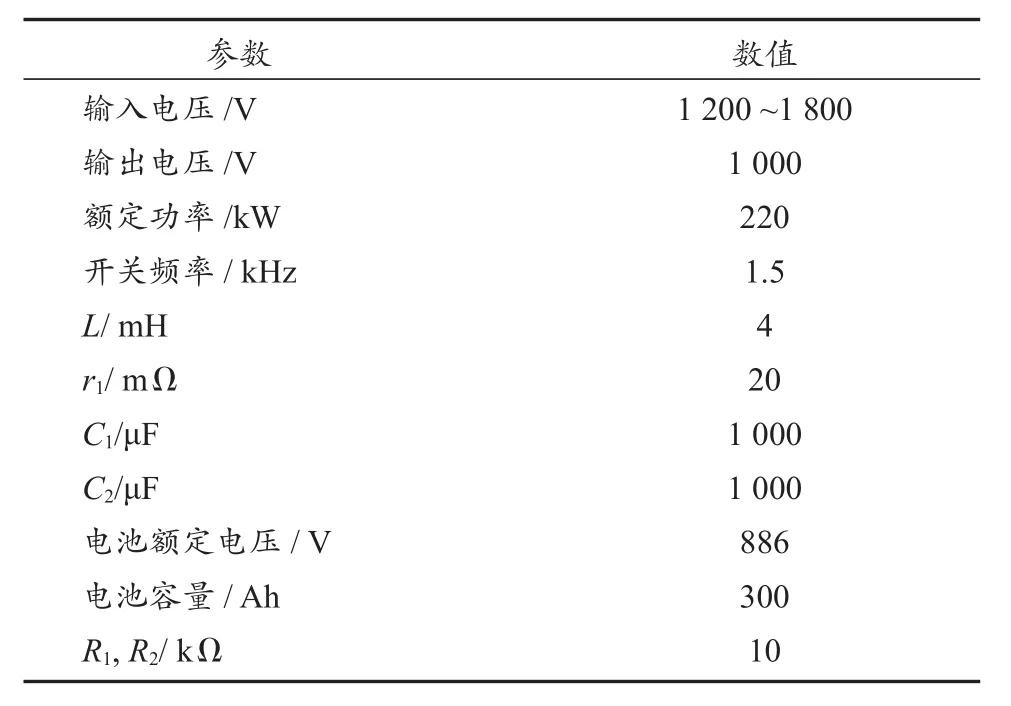
表1 仿真参数Tab. 1 Simulation parameters

图15示出充电过程分压电容器不均压时波形。在4 s时刻，撤销均压环，分压电容器C1和C2出现不均压现象，系统最终因压差大而触发停机保护功能，充电电流（即电感电流）降为0，验证了均压控制的有效性。

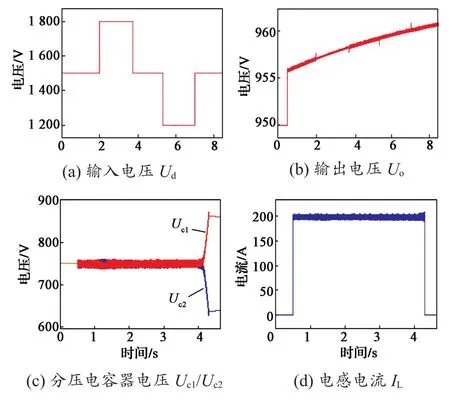
图 15 充电过程分压电容不均压实验波形Fig. 15 Unequal charging waveforms of the voltage dividing capacitor

图16示出网压跳变时的充电波形。可以看出，网压从1 500 V跳变到1 800 V，再跳到1 200 V，整个过程分压电容器电压平均值约为输入电压的一半，充电电流在网压跳变后迅速回到给定值200 A，表明系统抗网压波动能力强。

图 16 网压跳变时充电波形Fig. 16 Charging waveforms when network voltage jumps

图17示出网压注入200 V/100 Hz纹波电压时的充电波形。可以看出，整个过程分压电容的电压平均值约为输入电压的一半，蓄电池以最大充电电流（200 A）充电，电流低频纹波峰峰值约20 A，电压纹波小于1 V，表明系统均压效果好，对直流母线电压波动不敏感。

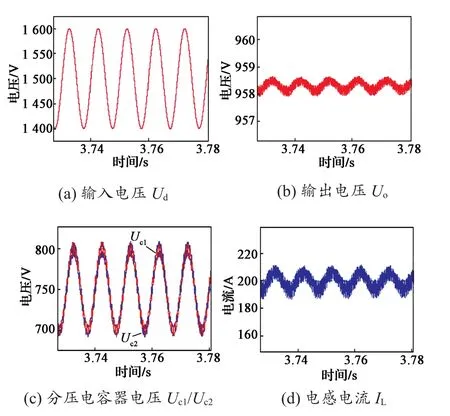
图 17 网压注入100 Hz纹波时充电波形Fig. 17 Charging waveforms when network voltage is injected with 100 Hz ripple

图18示出限流转恒压充电波形。可以看出，输出电压升至1 000 V后保持不变，充电电流平滑下降，闭环控制效果良好。

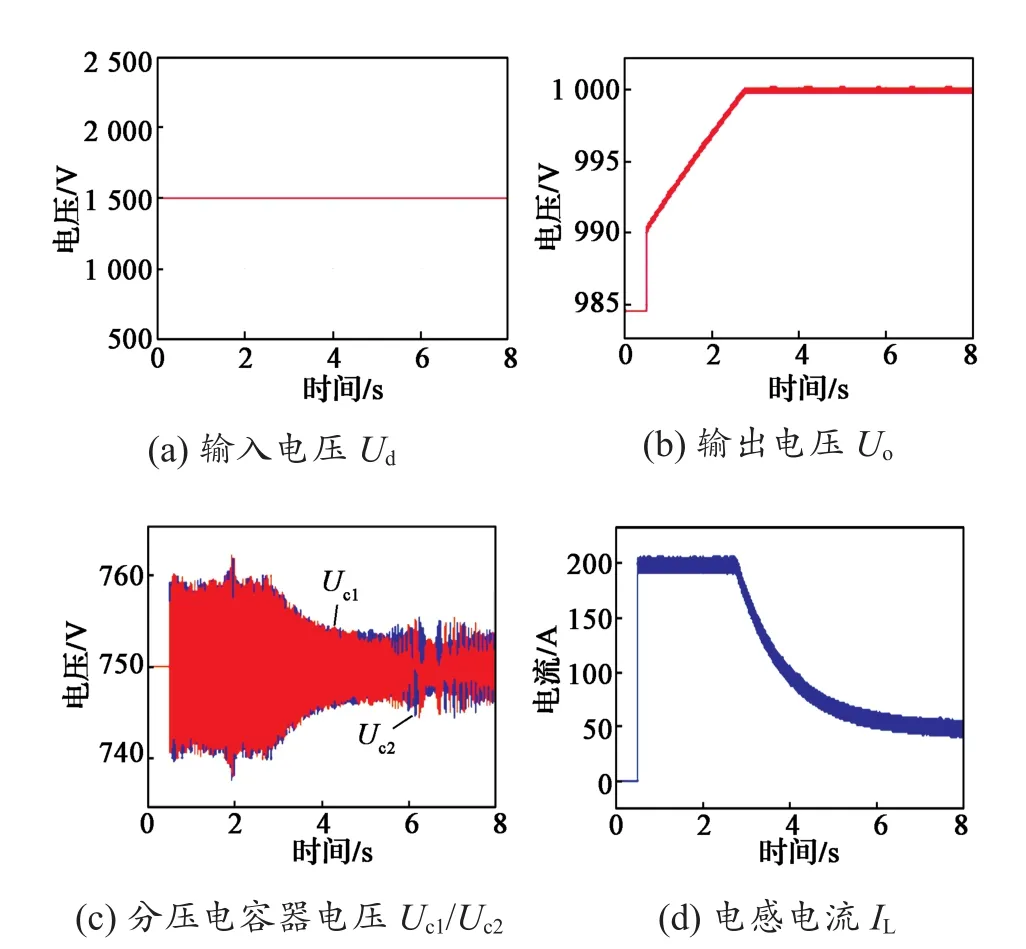
图 18 限流转恒压充电波形Fig. 18 Charging waveforms from current limiting to constant voltage

5 结语

本文基于状态空间法建立了输出端接动力蓄电池的三电平Buck变换器线性等效模型，设计了变换器闭环控制系统；并在Matlab环境下设计了1台220 kW的动力蓄电池充电机，以验证模型以及控制系统设计的有效性。结果显示，系统输出电流动态响应快，抗输入电压波动能力强。

该三电平Buck变换器建模与控制系统设计方法具备一定通用性，可以推广至其他Buck型变换器。但由于其采用PI控制，当输入端直流电压存在二次纹波时，纹波会传递到输出端，对蓄电池充电产生一定的影响，后续将研究这种工况下输出纹波电压的消除算法。