面向空中侦察调度的机场重要性分析

杨国利 成浩 温荟琦 刘伟

1.北京大数据先进技术研究院北京100195 2.解放军66136 部队北京100042

停驻于各个前沿机场电子侦察飞机是遂行多目标平时/战时侦察任务的主要手段, 当前正逐渐由单机作业向多机协同侦察转变, 其核心问题是多机协同下的侦察调度与任务规划.现代战争中,侦察调度与路径规划研究为解决多机多目标侦察问题提供了重要的技术支撑.受限于作战目的、战场环境、机场位置、飞机性能、功能属性等条件的约束,空中侦察调度需通过进行合理的任务规划来保证整个侦察任务的飞行总代价达到最优.

利用解决多旅行商问题(Multiple Travelling Salesman Problem, MTSP)[1−7]的方法思路, 研究多侦察机多目标条件下的空中侦察调度问题, 是一个切实可行的解决方案.目前应用较为广泛的算法包括: 遗传算法、蚁群算法、禁忌搜索算法、粒子群优化算法、模拟退火算法等.近年来,一些学者[1]通过对多无人机多目标侦察任务进行分析, 将无人机航路规划调度问题转化成多旅行商问题, 并利用改进的遗传算法对该问题模型进行智能寻优计算, 最终求得满足实际侦察需求的分配方案.文献[2]在研究多无人机协同搜索的航路规划问题中, 首先利用聚类算法将MTSP 问题分解成多个独立的旅行商问题(Travelling Salesman Problem,TSP)问题,再利用改进遗传算法求解问题模型, 提高了优化算法的计算效率.文献[3]综合考虑多种任务因素约束建立多无人机协同任务规划模型, 并提出改进的人工蜂群算法对其进行求解.

通过求解多旅行商问题, 人们可以获取各个飞机的调度方案和侦察路径, 同时也为衡量各个机场的重要性提供了量化手段, 用以指导节点重要性排序.众所周知,打击目标选择是联合作战指挥决策的重要环节, 同时也是弹目匹配和毁伤评估的前提和基础, 其工作质量对战争成败起着巨大作用.文献[8] 对联合作战条件下打击目标选择理论进行研究,给出了一种可操作性的系统分析方法.文献[9]从空袭作战理论角度分析影响空袭目标选择的影响因素,并建立模糊神经网络模型对重点目标进行重要性分析.此外,“对敌有效性”作为目标选择的重要指标通常被用来表征目标在敌方作战体系中的地位和作用,不同的目标选择对敌方作战体系影响不同[8].因此,在衡量各个机场重要性过程, 既需充分考虑这些目标本身的价值(停驻飞机数量、种类, 跑道长度),还需要考虑这些目标与其他目标共同作用产生的涌现特性[10].

为探索解决空中侦察调度与机场重要性问题,深度挖掘不同机场在空中侦察任务中的地位作用,本文主要对以下两个方面展开深入研究, 一是将空中侦察调度与路径规划问题转化成MTSP 问题, 通过对该问题进行分析建立相应模型, 并改进遗传算法进行最优路径求解; 二是通过节点移除法计算各机场目标失效后对整个体系空中侦察任务的影响,并选择出能够带来总飞行代价最大变化的关键机场.本文将任务优化和节点重要性分析相结合, 为任务驱动下的指挥决策提供了量化手段.

1 MTSP 问题

TSP 是组合优化算法中经典的NP-hard 问题[4],单个旅行商从某一城市出发,经过n个目标城市,除起始城市外必须且只访问一次其他城市, 最后再回到出发点.如何规划访问路线以使旅行成本代价最低是旅行商问题的关键.MTSP 是旅行商问题的延伸, 其假设有多个旅行商人, 要访问n个目标城市,除起始城市外必须且只访问一次其他城市.每个商人各从任一城市出发,经过不同的访问路线,最终回到各自出发点, 如何规划寻求各个旅行商最优的访问路线是该问题的关键.现实生活中很多问题都可转化为MTSP 问题[11−15],比如多无人机协同航路规划[1−3]、物流配送路径优化[5−7]问题等.其具体模型如下:

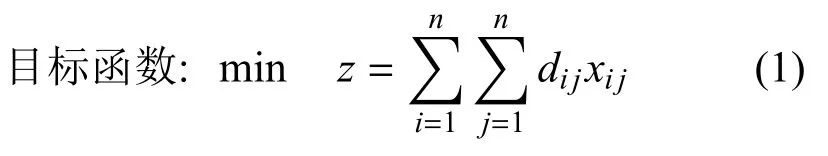
其中,z表示旅行商访问城市总路线的距离,di j表示从城市i到城市j的距离,xij表示从城市i到城市j的访问情况.

约束条件:每个城市必须且只能被访问一次,转化成数学表述即为式(2).

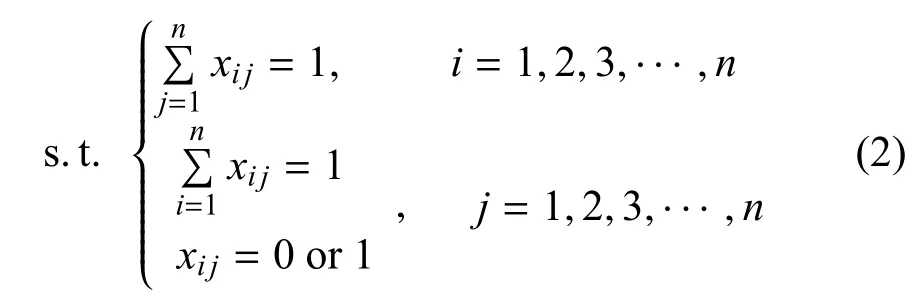
MTSP 问题可以通过枚举的方式求得最优解,但随着城市数目的增多,计算时间会急剧增加,无法满足算法的实用性需求,因此,必须选择合适的启发式优化算法, 在庞大的搜索空间中快速准确地找到最优可行解.

2 遗传算法

遗传算法是由自然界生物进化理论演变而来的一种群体寻优算法.它构成的种群具有自组织自适应的特征, 通过对构成的种群进行一系列评估、选择、交叉和变异等操作最终求得问题最优解.算法通用流程如图1 所示, 其中针对不同的问题如何设计科学的编码方式, 实现问题解空间与编码空间的一一对应, 是遗传算法首先需要解决的问题, 其次针对种群个体编码, 采取何种遗传操作有助于搜索最优解是算法的核心, 最后如何权衡搜索和利用(exploration vs exploitation)之间的关系,避免陷入局部最优是算法的重要环节.

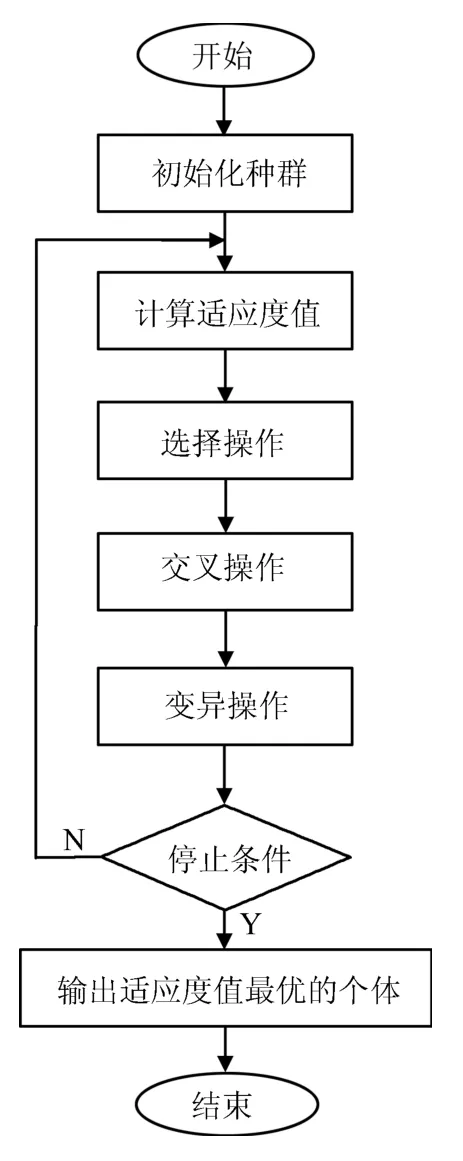
图1 经典遗传算法流程图Fig.1 Procedures of classical genetic algorithm

由于遗传算法不受搜索空间的约束, 无需复杂的推导过程,以适应度函数来引导整个搜索过程,对问题本身的依赖性很小[10],因此,该方法广泛运用于生物工程、生产调度、自动控制、工业工程和人工智能等领域.

3 问题建模

3.1 问题描述

停驻于前沿机场的各型电子侦察机是执行战场态势感知、探测电子信号、发现兵力动向的主要力量.一般情况下,电子侦察机的任务通常为从某一机场起飞, 沿规划好的路径飞抵沿途目标上空进行侦察并最终返回出发机场, 期间每架飞机仅需对部分目标实施侦察,其余目标则由其他飞机完成,最终需实现所有目标有且仅有一次被侦察.组织空中侦察任务需充分考虑侦察机的部署位置、最大航程、多机协同等问题, 合理分配各个执行侦察任务的飞机需要前往的目标以及先后次序, 使得整个侦察过程代价最小.

假设现有m个机场:A={A1,A2,··· ,Am}每个机场位置由唯一坐标点确定,即〈axi,ayi〉为机场Ai的坐标位置.

各个机场停驻的电子侦察机数目分别为n1,n2,··· ,nm,飞机数目总和为M=

i ni,即:

每架飞机最大航程为L, 存在映射函数θ :Pi∈P→Aj∈A表示各个飞机对应的机场.

现需调度侦察机实现对n个目标实施侦察,即:

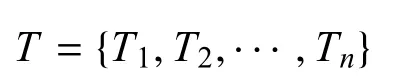
其中,每个目标的位置坐标记为〈txi,tyi〉.

任意两点之间的距离可通过下式求得:

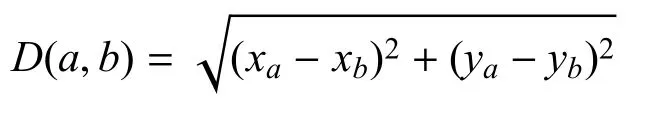
假设飞机在任意两点之间沿直线飞行, 每架飞机最大航程约束为L,飞机p飞行路径所包含的目标集合记为PTp,该集合中目标的排列顺序即为飞机的侦察次序,完成任务后返回出发基地,整个行程距离记为lp.将参与侦察任务的所有飞机飞行距离之和作为目标函数,得到如下表达式:

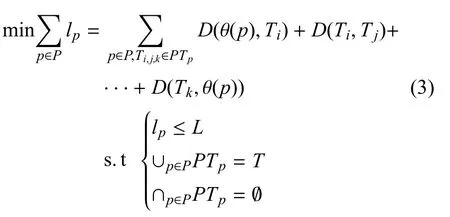
为实现所有目标有且仅有一次被飞机侦察且飞行路径之和最短, 需合理指派各个执行侦察任务的飞机沿特定顺序航线对目标进行侦察, 而如何实现“机场–飞机–目标” 之间的调度与路径规划是一个NP 难问题.

如图2 所示的侦察调度示例中, 机场A1 和A2分别驻有侦察机3 架和2 架,需要遍历6 个蓝色节点目标,其中机场A1 派出一架飞机沿路径A1 →T1 →T2 →T3 →A1 对T1、T2 和T3 进行侦察,机场A2派出一架飞机沿路径A2 →T5 →T4 →T6 →A2 对T4、T5 和T6 进行侦察.

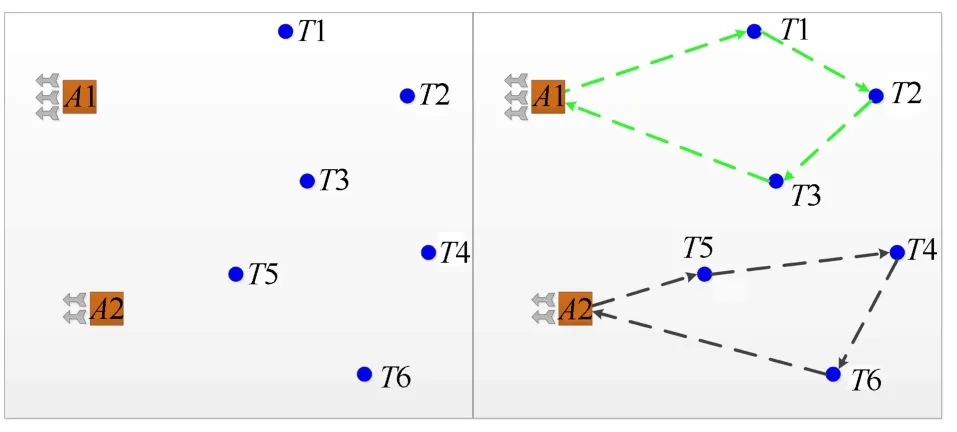
图2 空中侦察调度示意图Fig.2 A schematic diagram for aerial scout scheduling

3.2 模型分析

空中侦察调度与路径规划问题, 实质上是一个运筹学领域的寻优问题, 假设飞行空域没有空中禁区,且任意两点之间都可以沿直线飞行.通过对飞机侦察路径进行规划, 最终实现的优化结果主要需考虑满足以下因素:

1)参与任务的每架飞机按一定顺序飞抵其需要侦察的目标, 且各个任务飞机最后均需返回各自出发机场.

2)参与侦察任务的飞机飞行路径距离之和为模型的目标函数,旨在实现总距离的最短.

3)每个目标只被一架飞机进行一次侦察.

4)执行侦察任务的飞机飞行距离均满足最大航程约束.

MTSP 用于求解多个个体在多个地点之间的路线规划问题,其使每个个体从某地点出发,沿一条路线行进,使得每个地点有且仅有一个个体走过,最后所有个体回到原来出发地点,且总旅程最短.这类问题通常关注于让所有个体参与到地点遍历过程中,尽可能实现各个个体路径距离的平衡.上述各个机场的电子侦察机调度与路径规划问题, 可以抽象成一个典型的多旅行商问题,由于机场位置不同,各个机场停驻的飞机数量也不同,该问题具备以下特点:

1)需要明确哪些飞机将参与侦察任务.

2)需要规划飞机侦察目标的先后顺序.

3)需要确保飞机的飞行距离满足约束.

3.3 模型求解

鉴于遗传算法具有运算简单、快速收敛等特点,为求解该侦察调度优化问题, 研究尝试通过改进遗传算法搜索最优解,并针对问题背景特点,设计了可行的实现方法和操作流程.具体步骤包括: 1)种群个体编码; 2)目标函数设计;3)种群个体选择;4)个体交叉变异;5)局部优化搜索;6)选择最优个体.

种群个体编码: 需要具有问题解空间的完备特性,编码空间和解空间最好能够一一映射,将个体编码代入目标函数可产生相应的适应度值, 同时其还需体现个体的遗传特性.为实现上述目的,编码设计需能够同时满足飞机指派和飞行路径规划这两个问题背景,研究采用整数编码进行问题求解.

具体而言,每个个体包含两部分,一是对n个目标进行编码:记为[1,2,3···n];二是对m个机场中的全部飞机进行编码,飞机数目总和为M=i ni,故所有飞机的对应编码为[n+1,n+2,n+3···n+M],该编码中每一点位都对应唯一的停驻机场.将目标编码和飞机编码进行组合,得到一个编码长度为n+M的个体,其中,编码中数值大于n的点位表示飞机,数值小于等于n的点位表示侦察目标.为使个体编码能够完全表达问题解的形式, 定义某飞机点位n+i其后相邻且不间断的目标点位为该飞机需要侦察的目标PTi, 飞行路径为相应的目标点位先后顺序.例如, 编码为的个体片段中,数值为n+i的点位表示某飞机i,其后相邻点位为侦察目标,数值为2 和3 的点位表示该飞机需要侦察的目标T2和T3, 于是PTi= {T2,T3}, 假设该飞机位于机场Ai,那么其飞行路径为Ai→T2→T3→Ai;数值为n+j的点位表示某飞机j, 由于其后一点位数值不代表目标,于是PTj= ∅, 故该飞机不需要执行侦察任务.特别指出的是,如果某个体第一个点位数值不大于n, 则代表其为目标节点, 那么在对该个体进行解析时需将该个体编码向左进行平移, 直至第一点位数值大于n.通过平移操作,可以实现所有的目标点位都有相对应的飞机点位, 也保证了飞机侦察路径上包含了所有的目标.

如图3 示例中, 目标节点数目为n= 6, 即编码数值为{1,2,3,4,5,6}.机场数目为n= 2, 即A={A1,A2},其中,机场A1停驻飞机3 架,相应编码数值为{7,8,9}, 机场A2停驻飞机2 架, 相应编码数值为{10,11}.对于图3 所示个体,初始条件下生成的第1点位数值为5,表示目标节点,第2 点位数值为10,表示飞机节点,故解析该编码时需向左平移一位.平移后的个体编码中第3 点位和第8 点位数值分别为8和10,表示执行侦察任务的飞机节点,且其后相邻不间断的目标节点为对应飞机的飞行路径顺序, 即飞机8 的飞行路径记为:A1→T2→T3→T6→A1,飞机11 的飞行路径记为:A2→T1→T4→T5→A2.

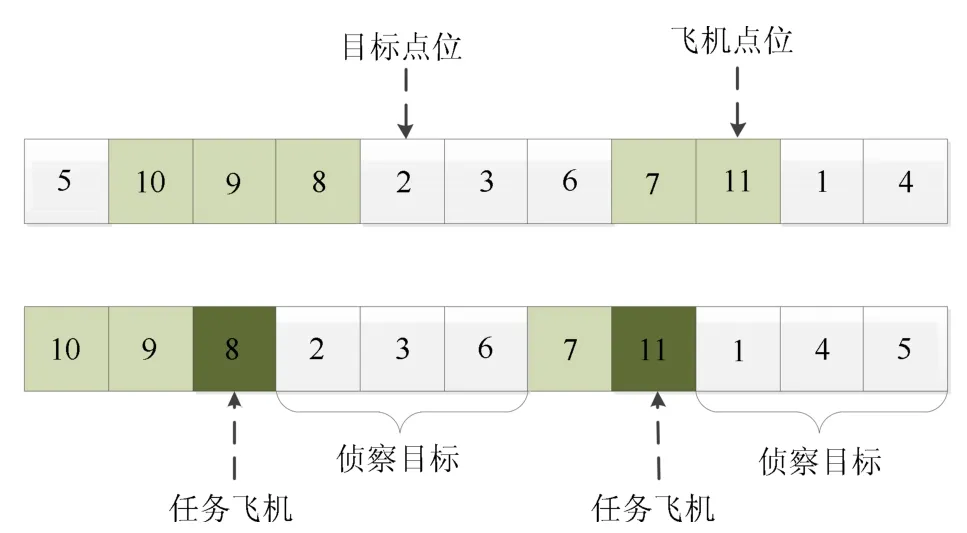
图3 遗传算法编码示意图Fig.3 A schematic diagram for the coding of genetic algorithm

目标函数设计: 能够针对每个个体编码生成相应的适应度, 并通过惩罚策略将约束条件引入目标函数中, 将带约束问题转化为无约束问题.本研究注重每架飞机的飞行距离小于其最大航程, 且所有飞机飞行距离之和最小.对于P= {P1,P2,··· ,PM}中的任一飞机Pi, 其在个体编码中对应的数值为n+i, 停驻机场为Aj= θ(Pi), 执行侦察任务的路径长度记为li, 飞行路径所包含的目标节点为PTi={Ts,··· ,Td},其中节点顺序即为飞行过程中的侦察顺序,那么该飞机飞行路径长度计算结果为:

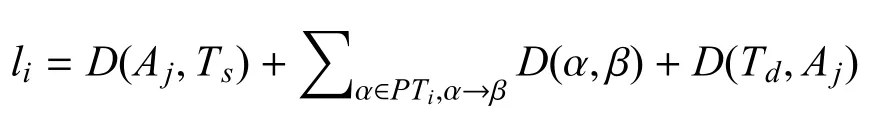
综上所述,所有飞行路径距离总和记为:

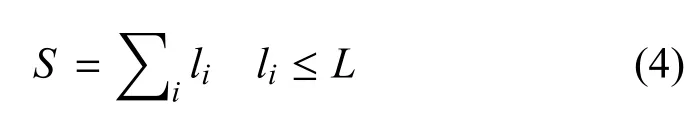
将约束条件带入目标函数中, 得到个体适应度计算表达式为:

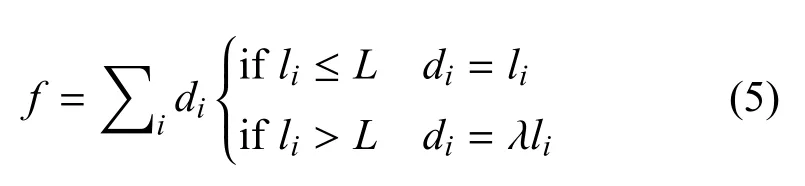
其中,λ>1 为违背约束条件的惩罚系数.

种群个体选择: 有利于将当前适应度较高的个体保留到下一代中,经典的方法包括轮盘赌方法、锦标赛方法、精英个体保留方法等.为确保最优个体遗传到下一代的同时, 适应度值大的个体也能尽量保留, 本研究采取精英个体保留方法与轮盘赌方法相结合的策略进行种群个体选择, 其中在整个种群中选择k个精英个体优先予以保留,然后按照正比选择的方法选取剩余N−k个个体.具体操作步骤为:

1)将当前种群中所有个体按照适应度大小顺序进行排序.

2)选取top-k个体进入下一代.

3)以概率选取种群中第i个个体进入下一代.

4)重复步骤3),直至下一代群体规模到达N.

个体交叉变异:是遗传算法的精髓,其通过对当前种群个体解进行交叉与变异,产生更优的个体.基于上述个体编码方式, 研究采用部分匹配交叉和反转变异的方式进行遗传操作,其中,交叉事件发生的概率为pc, 变异事件发生的概率为pm, 其主要模拟生物学中的基因突变,所以概率一般较低.

对于部分匹配交叉, 首先从种群中随机选取两个个体Ia和Ib,然后随机选择两个切点,将两个切点之间的点位片段互换,生成的两个新个体和由于新个体编码可能存在重复或遗漏,因此,需要对其进行相应的修复, 以恢复个体与解之间映射关系的合法性, 具体而言需要对交叉片段之外编码进行去重,并依次补入缺失的点位.在图4 所示的种群个体交叉过程示意图中, 由于交叉后的片段点位编码与已有点位编码相同(例如左侧个体中的编码4),同时又有一些编码存在缺失(例如左侧个体中的编码3),这就需要将已有片段中相同的编码进行去重, 同时将缺失的编码按顺序补入即可.

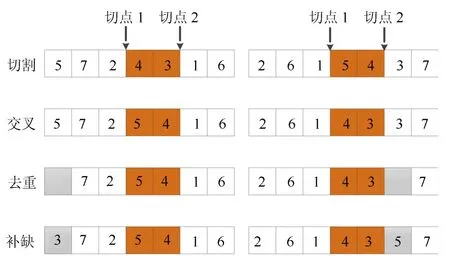
图4 种群个体交叉示意图Fig.4 A schematic diagram for crossover of individuals

对于个体变异操作, 该操作有利于增加种群多样性, 避免陷入局部最优.本研究采取反转变异, 具体而言需在个体中随机选择两个切点, 并将二者之间的点位编码完全反转如图5 所示.

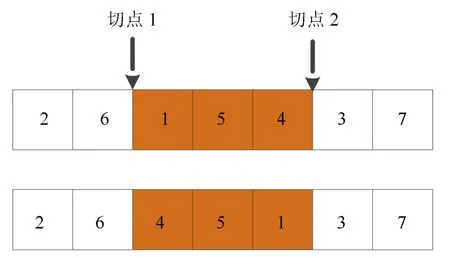
图5 反转变异操作示意图Fig.5 A schematic diagram for mutation of individuals

局部优化搜索: 是遗传算法中为了加速进化采取的一种操作,通过局部搜索针对一个较小的区域,致力于找到更好、更精确的解.一般来说,遗传算法在起始阶段注重广域搜索,随着迭代的进行,局部搜索的作用逐渐显现.在上述经典的遗传算法基础上,本研究对相邻侦察路径编码片段进行合并操作, 搜索其中性能最优的个体.通过局部优化搜索,能够减少无效的交叉变异操作, 驱动可行解向最优解方向移动,这也是改进遗传算法的核心.

例如在局部优化操作中, 随机选取一组相邻的飞行路径Pi+PTi和Pj+PTj,将二者合并共产生如下所示8 种可能路径, 进行局部优化搜索需从中选择最优方案:

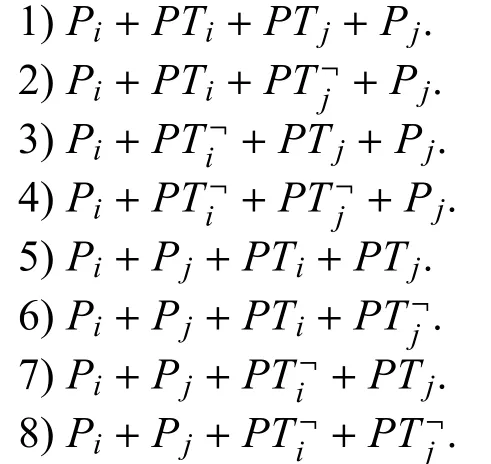
其中,为PTi编码的逆序.在下述案例中,某个体一段编码形式为[···n+i,2,3,n+j,4,5,n+k···],其中由飞机n+i进行侦察的目标编码为[2,3],由飞机n+j进行侦察的目标编码为[4,5],而且这两段编码相邻, 那么进行局部优化搜索需要将二者进行合并,生成一条新的路径,可行的合并方式如图6 所示.

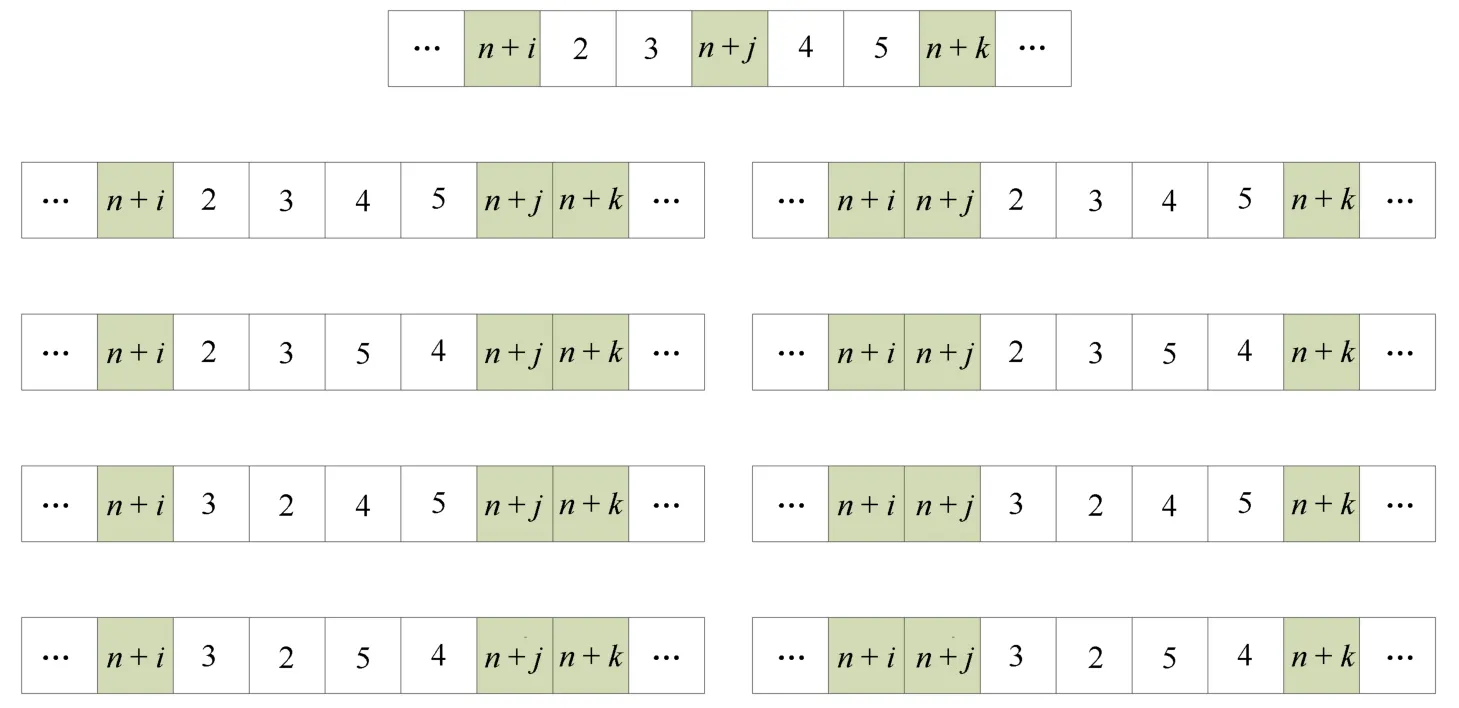
图6 局部搜索示例图Fig.6 A schematic diagram for local search

选择最优个体:在经过多次遗传迭代之后,在种群中选取性能最优的个体作为最终解.最终解的稳定性和收敛性是评价遗传算法的一项重要指标.

3.4 重要性排序

鉴于各个机场的位置不同, 且停驻的飞机数量也不相同, 为衡量各个机场在侦察调度中的重要性程度, 研究采取节点移除的方法, 从中移除某机场,然后求解剩余机场中飞机完成侦察任务的最小路径长度之和S.比较机场移除前后S的变化情况,即可确定该机场的重要性程度,即

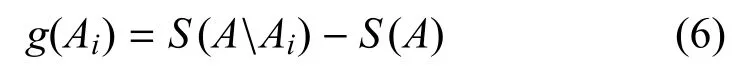
其中,S(A)为所有机场不变情况下最小路径长度之和,S(AAi)为移除机场Ai之后的最小路径长度之和.

4 案例分析

在本案例中,5 个机场共18 架侦察机需对20 个目标实施侦察,如图7 所示.

图7 机场与目标位置示意图Fig.7 The location map of airports and targets

本案例共有5 个机场A={A0,A1,A2,A3,A4},其坐标位置及停驻电子侦察机数目如表1 所示, 其中每架侦察机最大航程为L=3 000 km.

表1 机场坐标及飞机配置表Table 1 The coordinates and airplanes of airports

各电子侦察机需对20 个目标实施侦察,各个目标的位置数据为:

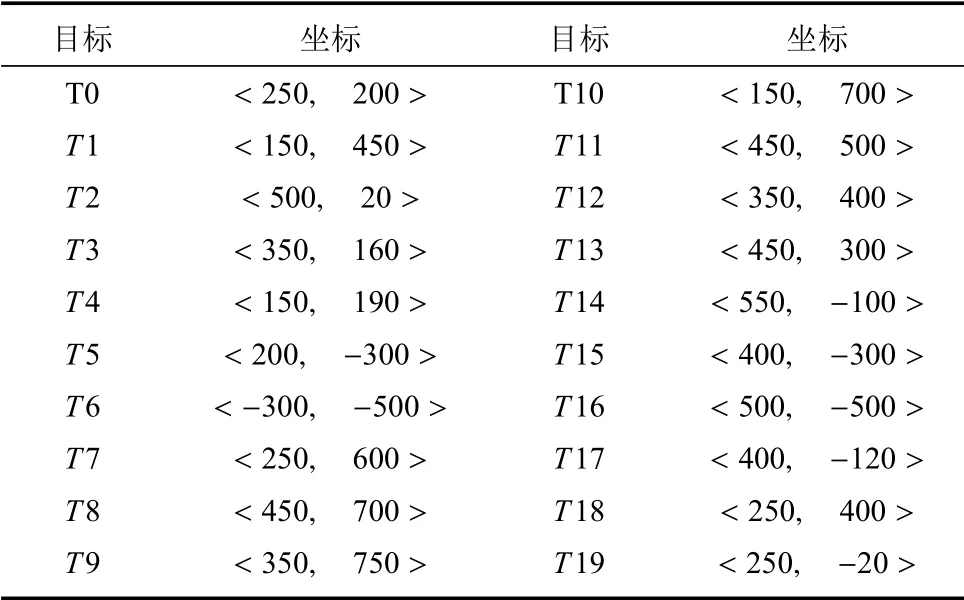
表2 侦察目标坐标位置表Table 2 The coordinates of targets

4.1 经典遗传算法

首先, 采用经典的遗传算法求解该问题, 其中编码方式、目标函数和交叉变异的操作如上所述,不进行局部优化操作.种群规模N= 200, 遗传代数T= 20 000, 交叉概率为pc= 0.5, 变异概率为pm=0.05,在精英保留和轮盘赌混合策略中选取top-3 最优个体优先予以保留,目标函数中违背约束条件的惩罚系数λ = 5.重复独立运行200 次实验, 得到一系列侦察路径最短距离,其均值与最大值、最小值如表3 所示.

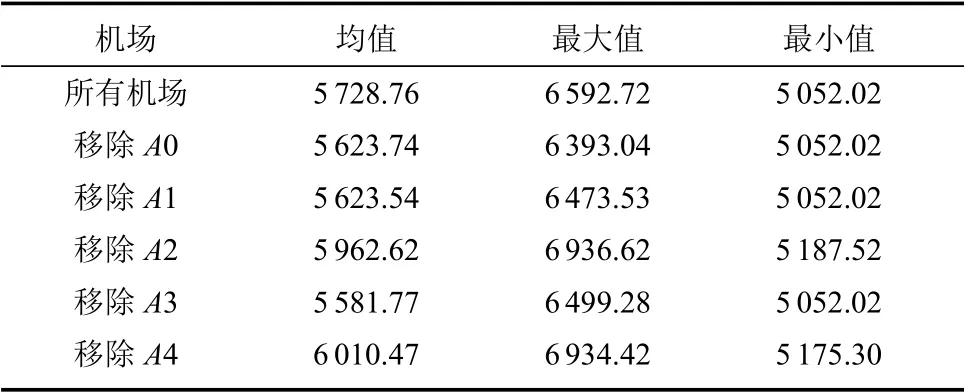
表3 经典遗传算法求解性能Table 3 Performance of classical genetic algorithm

运用经典遗传算法求解得到的最优解如图8 所示, 其中可以发现最优解依赖于从机场A2 和A4 起飞的飞机,其中,最优路径有两条,即:

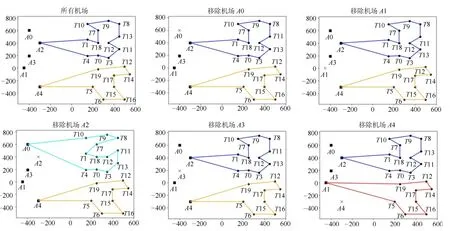
图8 不同情况下最优侦察路径示意图Fig.8 The optimal path for aerial scout in different cases

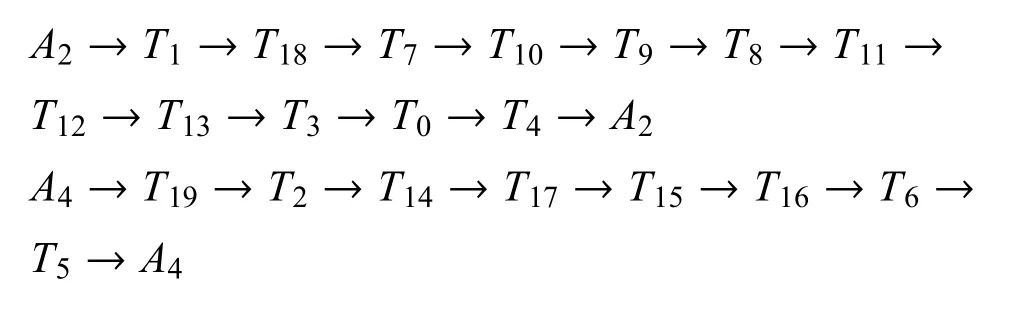
移除机场A2 和机场A4 对最优解的影响较大,故二者重要性较高, 整个机场重要性排序结果为:A2>A4>A0=A1=A3

4.2 改进遗传算法

在改进的遗传算法中, 编码方式、目标函数和交叉变异操作如上所述,同时增加局部优化操作.种群规模N= 200, 遗传代数T= 20 000, 交叉概率为pc= 0.5, 变异概率为pm= 0.05, 局部搜索概率为ps=0.2,在精英保留和轮盘赌混合策略中选取top-3最优个体优先予以保留, 目标函数中违背约束条件的惩罚系数λ = 5.重复独立运行200 次实验, 得到一系列侦察路径最短距离,其均值与最大值、最小值如表4 所示.

由表4 可以看出, 改进的遗传算法在求解性能上要优于经典的遗传算法, 尽管二者在侦察路径最短距离的最小值上并无差异, 但是通过加入局部优化搜索, 改进的遗传算法能够有效降低侦察路径最短距离的均值,使其更接近最优解.另外,机场A2 和A4 的移除,能够带来最短距离的提升,表明了二者在侦察任务中的重要地位.瘫痪机场A2 或A4 能够导致整个侦察任务性能的下降, 然而瘫痪其他机场则不会带来相应的变化, 凸显了任务优化和目标排序二者之间内在的关联.

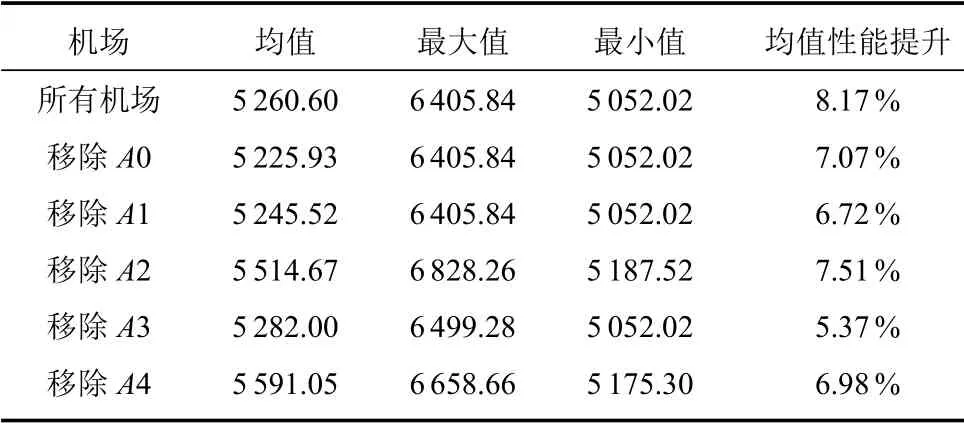
表4 改进遗传算法求解性能Table 4 Performance of improved genetic algorithm

5 结论

本文围绕多机场、多架次、多目标空中侦察调度和目标重要性分析问题, 以MTSP 问题为基础构建侦察机调度与路径规划模型, 并设计了一种改进的遗传算法对该模型进行求解, 来获取其最优的侦察目标分配方案和飞行航迹路线.为衡量不同机场在侦察任务中的重要程度, 本研究采用节点移除法量化某个机场瘫痪失效后, 对整个侦察任务完成性能的影响, 并以侦察飞行距离变化量为指标对机场目标进行重要性排序, 从而为目标选择和打击决策提供支持.最后,一系列实验结果验证了该方法的有效性和科学性.