基于改进遗传算法的工程项目多目标综合优化研究
刘颖聪,程圣东,2,张妙卿,吴文平
(1.西安理工大学 土木建筑工程学院, 陕西 西安 710048;2.西安理工大学 省部共建西北旱区生态水利国家重点实验室, 陕西 西安 710048)
工程项目多目标综合优化能够促进工程项目朝向精细化管理,建造工期、成本、质量相对优的项目,对工程项目管理工作的开展意义重大。但三者之间既对立又统一的关系,使得工程项目多目标综合优化变得困难。不过目前国内外学者仍然建立了一些关于工期-成本-质量多目标优化模型,取得了一定的成果。Bruce等[1]考虑工序的每一种时间成本组合的质量水平,采用层次分析法确定各个工序的权重和各个工序的质量水平得到整体工程项目的质量,同时结合标准的工期-成本模型,构建了工期-成本-质量模型,并通过实例验证了该模型的优越性。在随机网络计划图的条件下,Azaron等[2]建立了多阶段的工期、成本、质量多目标综合优化模型。在限定资源约束的情况下,Ziaratii等[3]研究了项目多目标优化问题,并进行模型求解。同时,比较模型优劣性。张连营等[4]提出了基于网络系统可靠度的质量模型,改进工程项目工期-成本-质量三者的均衡优化模型,并运用工程实例对该模型进行验证。卓锦松等[5]将质量水平量化为0-1的连续数值,设置高、低质量水平及质量变化率进行质量量化建立多目标优化模型。
本研究试图利用价值工程理论进行质量模型的量化,同时对成本进行动态量化改进,从而改进了工期-成本-质量三者的综合优化模型。为便于工期-成本-质量模型的构建及计算,针对该问题提出以下假设:
假设1 各项工序的施工顺序保持不变,当某项工序存在多个紧前工序时,各个紧前工序相互独立,则只要任意一个紧前工序未完成或未达到要求质量水平,均会对后续工序产生直接影响。
假设2 压缩项目工期时,不可将关键工作变成非关键工作,且关键工作持续时间不能小于完成该工作所需的最短持续时间。
假设3 各项工序的间接成本仅与工期产生关系,并认为项目间接成本与工期之间的关系呈折线型递增。本模型认定项目总成本为直接成本与间接成本之和,并且不考虑环境、施工技术复杂度等不确定因素对其产生影响。
1 工期-成本优化模型
在工程项目多目标优化研究中,对于工期-成本优化模型的研究已经相当成熟。本文所建立的工期-成本优化模型:在工期上以网络计划为基础,根据传统的关键路径法计算工程完工的总时间。在成本上,将项目成本分为直接成本与间接成本,并考虑提前完工减少间接成本和拖延工期增加间接成本的情况,对间接成本进行修正。同时考虑成本变动涉及资金的流动,添加资金的时间价值更加符合工程实际[6]。
从直接成本与工期的关系来分析,该研究以工序为基本单元研究项目直接成本与进度的函数关系,项目直接成本是工序直接成本的总和,并参考Deckro[7]于1995年率先提出并验证的工序持续时间-成本的二次方关系,则工序(i,j)直接成本的表达式如下:
Cij=Cnij+αij(tnij-tij)2
αij=(Csij-Cnij)/(tnij-tsij)2
(1)
式中:αij为边际成本递增因子;tnij为工序(i,j)的正常工期;tsij为工序(i,j)的极限工期;tij为工序(i,j)的实际持续时间;Cij为工序(i,j)的实际直接成本;Cnij为工序(i,j)的正常工期下直接成本;Csij为工序(i,j)的极限工期下直接成本。
间接成本以施工管理费为主展开,当工期变化时,施工管理费呈线性关系,它一般会随着工期的缩短而减少,由此本文假定间接成本与工期为线性关系。考虑工程实际情况,在合同工期前,业主一般会设置提前完工奖励以激励承包商提前完工,这就相当于间接成本有所减少;同样地,在合同工期后,业主一般会规定延期惩罚,这就相当于间接成本有所增加[8]。因此经修正的间接成本与工期呈现折线关系,则间接成本的表达式如下:
(2)
式中:CJX为间接成本;TR为项目的合同工期;T为项目的实际工期;T1为项目允许的最短工期;T2为项目允许的最长工期;β为项目间接成本费率,元/d;βH为项目落后合同工期一天惩罚费用;βQ为项目提前合同工期一天奖励费用。
综上所述,在考虑资金时间价值的情况下,假设资金的时间价值以连续复利的形式记取,值得注意的是,间接成本采用费率摊到每个计算周期内,应采用等额现值费率计算,但由于公式求取总成本,故简单将其以完工时统一进行一次现值计取。因此,成本的动态优化数学模型如下:
e-rT[(Tβ-(TR-T)βQ)(1-λ)+(Tβ+(T-TR)βH)λ]
(3)
约束条件:
tsij≤tij≤tnij,C≤Cp
式中:C为工程费用计算值;Cp为工程费用计划值;r为工程计算周期名义利率;dij为每一道工序开始的时间。
2 质量量化模型
工程项目质量的量化工作一般是在项目结束后由相关部门进行验收评定,然而工程项目多目标优化工作则要求在项目前期展开。由于两者工作存在时间跨度差且质量本身难以量化的特点等原因,导致工程多目标优化工作难以开展。本研究在引入价值工程和QFD理论的基础之上,以功能系数代表质量水平[9],对质量目标进行量化。
2.1 价值工程理论应用于质量量化的可行性分析
价值工程是一门新兴的管理技术,旨在以最低的寿命周期成本实现产品的必要功能。它是一种以提高产品价值为目标的定量化的分析方法,着重强调进行功能分析,从而有组织开展活动。价值工程从研究对象功能与成本之间的匹配关系出发,在分析研究对象功能的基础上来探讨研究对象的结构、材质等问题,是一种十分有效的技术分析方法[10]。价值工程理论涉及三个核心概念:功能、成本、价值。价值工程系数计算如下:
(4)
公式(4)反映了价值、功能、成本三者之间的辩证关系,载体的功能与成本成负相关的关系,与价值系数成正相关的关系。经计算的价值系数存在3种情况,即V大于1、等于1、小于1。通常来说,只有当V等于或近似等于1时,就认为成本与功能之间的关系为合理匹配,此时评价对象达到最佳价值。通常以成本改善值来衡量成本与功能匹配关系的变化。
某个评价对象成本改善值的计算方法为实际成本减去其功能评价值,即:
ΔCi=Ci-Fi
(5)
成本改善值也有三种情况:ΔCi>0;ΔCi=0;ΔCi<0。 ΔCi=0时,说明实际成本等于功能测评值,功能与成本合理匹配。
在项目施工中,项目成本及工期可看作是项目的投入,质量是各种资源安排后的结果。应用价值工程进行施工质量量化的基本思路是:通过缩短工期和降低成本以保证施工质量达到设计要求,从而来提高工程价值目的。在价值公式中,功能是指产品本身所具有且能够带给用户满足和愉悦感觉的用途性质。工程项目的功能范畴包括坚固耐用程度、防水排水能力、结构通畅性、舒适程度、协调美观度等,同时这些功能也是工程质量的基本属性。因此,广义的工程项目质量水平可以代替工程项目的功能水平[11]。成本要素主要包括人工费、材料费、机械使用费,在建立质量目标优化模型时,用实际直接成本与正常直接成本的比值表示。
经过上述分析,项目功能可以间接看作项目的质量,通过与项目成本进行比较,可以清晰的衡量项目整体质量的好坏。
2.2 基于价值工程理论的质量量化模型
工程项目的总质量最终是由每道工序质量决定的。因此,在论证价值工程理论可以进行质量量化的基础之上,建立工程项目工序(i,j)的价值工程质量量化模型,如下式:
(6)
式中:Vij为工作(i,j)的价值工程系数;Fij为工作(i,j)的功能系数。
其中,工作(i,j)的功能系数计算如下:
(7)


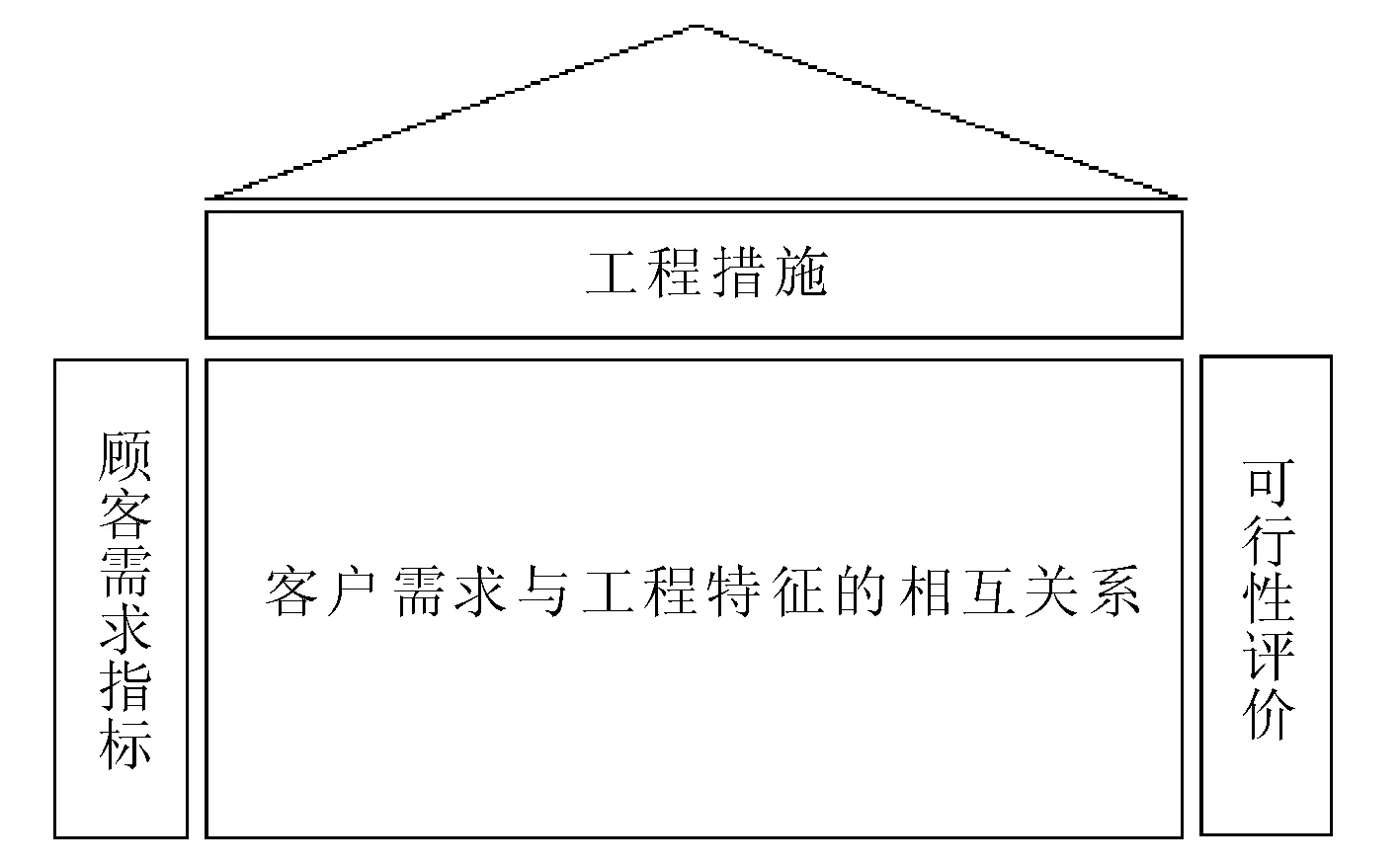
图1 基本质量屋模型
工程项目质量特性为适用性、安全性、可靠性、耐久性、经济性与环境的协调性。值得注意的是,某项工序虽不能体现质量的所有特性,可能只含几项,但最终由其构成的整体工程应体现所有的质量特性。同时在QFD概念的基础上,运用“质量屋”模型进行专家打分计算,将其客户需求指标替换为工程项目的各项活动,可行性评价替换为各个活动的功能系数打分,所构建的基本模型如图2所示。
(8)
(9)
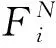
综上,质量目标优化模型可以表示为:
(10)
约束条件:
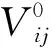
3 工程项目工期-成本-质量综合优化模型
通过上述分析,为了实现工程项目工期-成本-质量的多目标优化的目的,使项目总体水平达到最优或近似最优的状态[13],即使工期最短,成本最低,质量水平最高。本文建立工程项目多目标优化模型为:
(TR-T)βQ)(1-λ)+(Tβ+(T-TR)βH)λ]
(11)
(12)
(13)
约束条件:
tsij≤tij≤tnij
Cij≥0,C≤Cp
4 基于Pareto排序的遗传算法求解
本文考虑基本遗传算法存在计算量大,需要较大的进化代数和花费较长的计算时间[14 ]的缺陷上,采用基本遗传算法和基于Pareto排序[15 ]的思想来改进分配适应值的方法,从而进行求解,并用MATLAB软件来实现,其主要步骤为:
(1) 初始化参数,以确定初始群体及遗传操作过程,即确定项目参数和遗传算法的基本参数。
(2) 随机生成初始群体,在不包含决策者的意愿情况下,在问题解集内随机生成初始群体。
(3) 计算目标值,利用各个目标函数确定相应代数的目标值。
(5) 遗传算子操作,根据轮盘赌法的策略选择,进行复制以及交叉操作,得到下一代,依次循环迭代,直到满足终止条件。
(6) 输出,当满足迭代次数,输出结果,即Pareto最优解集。
5 工程实例应用分析
5.1 工程概况


表1 工序逻辑关系及相关参数值

图3 项目双代号网络图
5.2 模型建立及求解
根据表1,考虑该项目工期为240 d,时间较短,在建立模型时不考虑资金的时间价值的影响。本工程项目的工期、成本、质量目标优化模型建立如下:
(14)
(4894T-718560)λ
(15)
(16)
约束条件:
tsij≤tij≤tnij
Cij≥0,C≤29 939 285
5.3 结果分析
运用MATLAB编程,设置种群规模取300,种群代数为200次,交叉概率取0.9,变异概率取0.1。在程序实现过程中,迭代次数达到200次的时候,得到成本-工期-质量权衡分析最能体现三者关系,呈现出的图形效果最佳,其Pareto解集分布状况如图4所示。

图4 成本-工期-质量权衡分析Pareto解集
通过观察该图可得,该模型结果与实际工程情况贴近,即随着工期压缩,成本增加,质量水平相应提升。为了直观起见,表2列出了模型计算得到的Pareto最优解样本示例及结果比较,为决策者在可供选择的决策范围内提供最优方案。由此,决策者可以结合实际工程情况选择满足要求的实施方案。经过优化,项目最短工期为215 d,工期相对合同工期缩短25 d,相应成本比预期成本减少383 505元;最长工期为223 d,工期相对合同工期缩短17 d,成本减少430 502元。
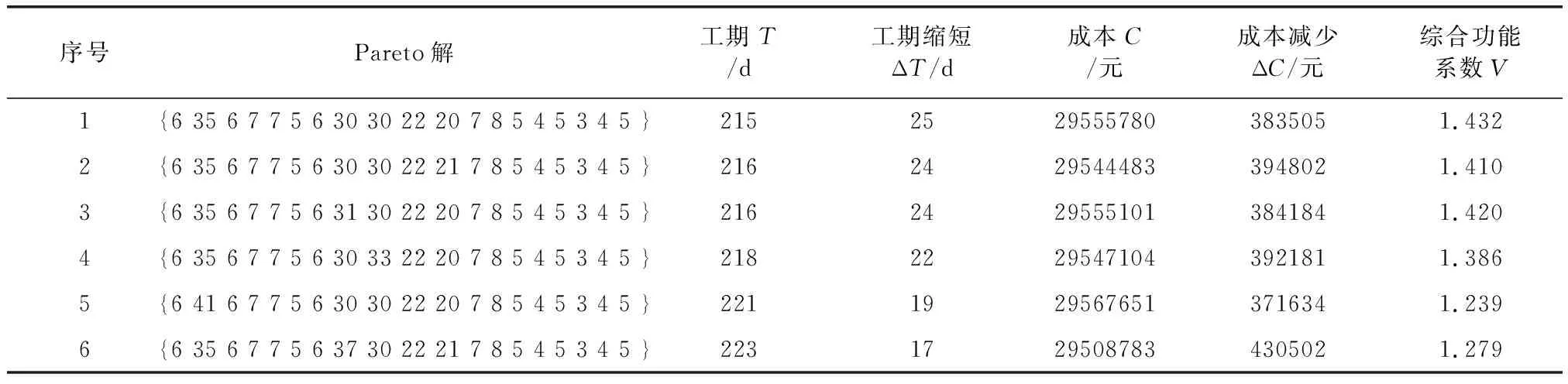
表2 Pareto最优解样本示例及结果比较
6 结论及展望
本研究借鉴前人的研究成果,有以下两点改进之处:其一,通过对间接成本改进,同时为更加贴合实际,考虑资金的时间价值,建立改进的工期-成本模型。其二,利用价值工程理念和QFD质量度量模型,建立了工程质量量化模型,对工程项目多目标优化模型进行分析。综合以上两点,提出了一种新的工期-成本-质量优化模型。但要说明的是,该模型仍具有一定的局限性:由于在建立工期-成本-质量优化模型的过程中,进行大量的假设,忽略了一些看似不变及次要的影响因素。然而,在实际工程项目管理中诸多因素都会影响着项目最终价值的实现。因此,需要结合大量的工程实践数据,分析研究各个目标间的变化关系,进一步完善多目标优化模型。

