集值向量均衡问题近似有效解的最优条件
孟旭东
(南昌航空大学科技学院,江西共青城332020)
向量均衡问题主要包括向量优化问题、向量变分不等式问题、向量鞍点问题、向量相补问题等,是运筹学和非线性分析研究的热点问题之一,备受学者青睐,已有较丰硕的研究成果[1-18]。
GONG[1-3]在锥-凸假设前提下,得到了具约束向量均衡问题的最优条件,并运用非线性标量化方法刻画了非凸向量均衡问题弱有效解、Henig有效解、超有效解及Global有效解的充分必要条件。LUU等[4-5]建立了具等式和不等式两类约束的向量均衡问题有效解的最优定理,并在适当凸性条件下,得到了具约束向量均衡问题局部有效解的Kuhn-Tucker型必要条件。
通常,在对实际问题进行建模求解时,得到的为近似有效解。因此,研究现实问题近似有效解的性态具有重要价值和深远意义。LORIDAN[6-7]介绍了广义向量优化问题近似有效解的概念,随后,LI等[8]引入含参向量均衡问题近似有效解概念,并建立了最优定理。凸性在研究向量均衡问题中扮演着重要角色。GONG[9]在局部凸空间中,借助锥-凸性研究了具约束集值向量均衡问题的Henig有效解、Global有效解和超有效解的充分必要条件;最近,YANG等[10-11]给出了近似锥-次类凸和广义锥-次类凸集值映射的概念,并讨论了它们的关系;SACH[12]借助内部锥-次类凸性,建立了向量优化问题有效解、弱有效解和Benson真有效解的Kuhn-Tucker型和Lagrange型最优定理;XU等[13]提出了近似锥-次类凸集值映射的概念,证明了近似锥-次类凸性是迄今为止一类更为广义的凸性,并在此条件下给出了强有效解的Kuhn-Tucker型最优条件和超有效解的Lagrange型最优的充分条件;在广义不变凸性条件下,文献[14-16]从不同角度研究了集值优化问题解集的最优性条件;孔翔宇等[17]在广义不变凸性假设下,建立了集值优化问题弱近似解的最优定理;LONG等[18]借助XU等[13]提出的近似锥-次类凸性概念,运用凸集分离定理,在实局部凸Hausdorff拓扑向量空间中建立了具约束向量均衡问题的Henig有效解和超有效解的Kuhn-Tucker型最优定理。
本文在文献[1,9,18]研究成果基础上,研究实局部凸Hausdorff拓扑向量空间一类具约束集值向量均衡问题近似有效解的最优条件,推广了文献[1,9,18]中的一些研究结论。
1 准备工作
设X为实拓扑向量空间,Y,Z均为实局部凸Hausdorff拓扑向量空间,Y*,Z*分别为Y,Z的拓扑对偶空间,C⊆Y,D⊆Z皆为闭凸点锥,且满足其拓扑内部intC≠∅,intD≠∅。记C*,D*分别为C,D的拓扑对偶锥,C#为C*的拟内部,定义:
C*:={f∈Y*:f(c)≥0,c∈C},D*:={g∈Z*:g(d)≥0,d∈D},
C#:={f∈Y*:f(c)>0,c∈C{0}}。
设M⊆Y为非空子集,M的锥包为cone(M):={λm:λ≥0,m∈M}。称 非 空 凸 子 集B⊆C为凸锥C的基当且仅当0∈cl(B),C=cone(B)。C#≠∅当且仅当凸锥C有基。记
CΔ(B):={f∈C#:b∈B,∃t>0,s.t.f(b)≥t},由凸集分离定理,得CΔ(B)≠∅,且CΔ(B)⊆C#。设B为C的基,则0∈cl(B),存在f∈Y∗{0Y*},使得实数
r=inf{f(b):b∈B}>0,则为Y中零点的开凸邻域,且inf对Y中零点的每个凸邻域U⊆VB,有B+U为凸集且0∈cl(B+U),故CU(B):=cone(B+U)为 点 凸 锥 且 满 足C{0}⊆intCU(B)。
设X0为X的非空凸子集,G:X0→2Z为X0上的集值映射,Φ:X0×X0→2Y为X0×X0上的集值映射。记从Z到Y的所有连续线性算子的全体为L(Z,Y),将L(Z,Y)的子集L+(Z,Y)定义为
L+(Z,Y)={T∈L(Z,Y):T(D)⊆C},记A={x∈X0:G(x)∩(-D)≠∅}。
考虑约束集值向量均衡问题(简称问题(ΦSVEPC)):
给定点x0∈A,使得
Φ(x0,y)∩(-K)=∅,y∈A,
其中,K∪{0}为Y中的凸锥。
定义1 设G:X0→2Z,Φ:X0×X0→2Y为给定集值映射,给定点x0∈A,
(1)若存在零点的邻域U⊆Y,满足U⊆VB,使得
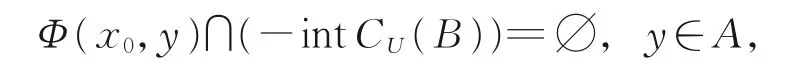
则称点x0为问题(Φ-SVEPC)的Henig有效解,并将问题(Φ-SVEPC)的所有Henig有效解的全体记为VH(Φ,A)。
(2)若存在点凸锥H⊆Y,满足C{0}⊆intH,使得

则称点x0为问题(Φ-SVEPC)的Global有效解,并将问题(Φ-SVEPC)的所有Global有效解的全体记为VG(Φ,A)。
定义2 设G:X0→2Z,Φ:X0×X0→2Y为给定集值映射,给定点x0∈A,ε≥0,
(1)设B为C的基,点e∈B,若存在零点的邻域U⊆Y,满足U⊆VB,使得
(Φ(x0,y)+εe)∩(-intCU(B))=∅,y∈A,则称点x0为问题(Φ-SVEPC)的ε-Henig有效解,并将问题(Φ-SVEPC)的所有ε-Henig有效解的全体记为VH(Φ,A,ε)。
(2)设点e∈C{0},若存在点凸锥H⊆Y,满足C{0}⊆intH,使得
(Φ(x0,y)+εe)∩(-H{0})=∅,y∈A,则称点x0为问题(Φ-SVEPC)的ε-Global有效解,并将问题(Φ-SVEPC)的所有ε-Global有效解的全体记为VG(Φ,A,ε)。
设F:X0→2Y为给定集值映射,考虑以下集值优化问题(简称问题(SOP)):
在问题(SOP)中,总假设可行集A⊆X0非空,并记
定义3 设F:X0→2Y为给定集值映射,点x0∈A为问题(SOP)的可行点,
(1)若存在零点的邻域U⊆Y,满足U⊆VB以及点y0∈F(x0),使得
(F(A)-y0)∩(-intCU(B))=∅,
则称点x0为问题(SOP)的Henig有效解,并称点(x0,y0)为问题(SOP)的Henig有效对。
(2)若存在点凸锥H⊆Y,满足C{0}⊆intH以及点y0∈F(x0),使得
(F(A)-y0)∩(-H{0})=∅,
则称点x0为问题(SOP)的Global有效解,并称点(x0,y0)为问题(SOP)的Global有效对。
定义4 设F:X0→2Y为给定集值映射,点x0∈A为问题(SOP)的可行点,ε≥0,
(1)设B为C的基,点e∈B,若存在零点的邻域U⊆Y,满足U⊆VB以及点y0∈F(x0),使得
(F(A)-y0+εe)∩(-intCU(B))=∅,
则称点x0为问题(SOP)的ε-Henig有效解,并称点(x0,y0)为问题(SOP)的ε-Henig有效对。
(2)设点e∈C{0},若存在点凸锥H⊆Y,满足C{0}⊆intH以及点y0∈F(x0),使得
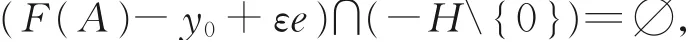
则称点x0为问题(SOP)的ε-Global有效解,并称点(x0,y0)为问题(SOP)的ε-Global有效对。
设F:X0→2Y,G:X0→2Z为 给 定 集 值 映 射,T0∈L+(Z,Y),考虑以下不具约束的集值优化问题(简称问题(USOP)):
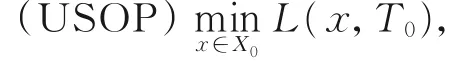
其 中 ,L(x,T0)=F(x)+T0(G(x)),(x,T0)∈X0×L+(Z,Y),且 对 每 个T0∈L+(Z,Y),记L(X0,T0)=x∪∈X0L(x,T0)。
定义5 设F:X0→2Y,G:X0→2Z皆为给定的集值映射,算子T0∈L+(Z,Y),且点x0∈X0为问题(USOP)的可行点,
(1)若存在零点的邻域U⊆Y,满足U⊆VB以及点y0∈F(x0),使得
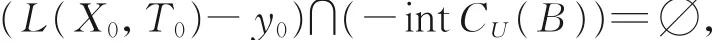
则称点x0为问题(USOP)的Henig有效解,并称点(x0,y0)为问题(USOP)的Henig有效对。
(2)若存在点凸锥H⊆Y,满足C{0}⊆intH以及点y0∈F(x0),使得
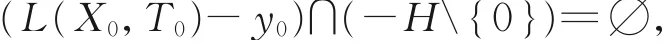
则称点x0为问题(USOP)的Global有效解,并称点(x0,y0)为问题(USOP)的Global有效对。
定义6 设F:X0→2Y,G:X0→2Z皆为给定的集值映射,算子T0∈L+(Z,Y),且点x0∈X0为问题(USOP)的可行点,ε≥0,
(1)设B为C的基,点e∈B,若存在零点的邻域U⊆Y,满足U⊆VB以及点y0∈F(x0),使得

则称点x0为问题(USOP)的ε-Henig有效解,并称点(x0,y0)为问题(USOP)的ε-Henig有效对。
(2)设点e∈C{0},若存在点凸锥H⊆Y,满足C{0}⊆intH以及点y0∈F(x0),使得
(L(X0,T0)-y0+εe)∩(-H{0})=∅,则称点x0为问题(USOP)的ε-Global有效解,并称点(x0,y0)为问题(USOP)的ε-Global有效对。
定义7 设F:X0→2Y为给定集值映射,若对任意的点x1,x2∈X0及λ∈[0,1],使得
λF(x1)+(1-λ)F(x2)⊆F(λx1+(1-λ)x2)+C,则称F在X0上为C-凸集值映射。
定义8[10-11]设F:X0→2Y为给定集值映射,若存在点θ∈intC,使得对任意的点x1,x2∈X0及λ∈[0,1],α>0,存在点x3∈X0,满足
αθ+λF(x1)+(1-λ)F(x2)⊆F(x3)+C,则称F在X0上为近似C-次类凸集值映射集合当且仅当集合clcone(F(X0)+C)为凸集。
设Ψ:X0×X0→2Y为给定集值映射,考虑以下不具约束的集值向量均衡问题(简称问题(ΨUSVEP)):
给定点x0∈X0,使得
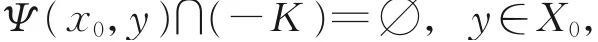
其中,K∪{0}为Y上的凸锥。
定义9 设Ψ:X0×X0→2Y为给定集值映射,x0∈X0为给定点,ε≥0,
(1)设B为C的基,点e∈B,若存在零点的邻域U⊆Y,满足U⊆VB,使得(Ψ(x0,y)+εe)∩(-intCU(B))=∅,y∈X0,则称点x0为问题(Ψ-USVEP)的ε-Henig有效解,并将问题(Ψ-USVEP)的所有ε-Henig有效解的全体记为VH(Ψ,X0,ε)。
(2)设点e∈C{0},若存在点凸锥H⊆Y,满足C{0}⊆intH,使得
(Ψ(x0,y)+εe)∩(-H{0})=∅,y∈X0,则称点x0为问题(Ψ-USVEP)的ε-Global有效解,并将问题(Ψ-USVEP)的所有ε-Global有效解的全体记为VG(Ψ,X0,ε)。
2 近似有效解的性质


3 Kuhn-Tucher型最优条件
在近似锥-次类凸假设下,建立集值向量均衡问题Henig近似有效解和Global近似有效解的Kuhn-Tucher型最优性定理。
定 义10 设G:X0→2Z,Φ:X0×X0→2Y,φ:X0→2Y×Z为 给 定 集 值 映 射,x0∈X0为 给 定点,ε≥0,
(1)设B为C的基,点e∈B,对任意的点x∈X0,称φB(x)=Φ(x0,x)+εe,G(x)为X0上 关于B的有序对集值映射。




由 点 (0Y,0Z)∈clcone(φB(X0)+C×D) 及 式(10),得



(3)将文献[1]中集值函数φB的锥-凸性减弱为近似锥-次类凸性。
推论4 若满足条件(K3)、(K4)和(H4),则存在(f,g)∈CΔ(B)×D*,使得


4 Lagrange型最优条件
在近似锥-次类凸假设下,建立集值向量均衡问题Henig近似有效解和Global近似有效解的Lagrange型最优定理。
设G:X0→2Z,Φ:X0×X0→2Y为给 定 集 值映射,T0∈L+(Z,Y),Ψ:X0×X0→2Y定义为
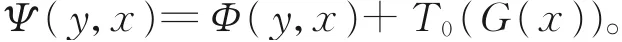
为保持表述的一致性,给出以下基本假设。
(L 1)点x0∈A,y0∈F(x0);
(L 2)点(x0,y0)为 问 题(SOP)的ε-Henig有效对;
(L 3)点(x0,y0)为 问 题(SOP)的ε-Global有效对;
(L 4)存在算子T0∈L+(Z,Y),使得点x0为问题(Ψ-USVEP)的ε-Henig有效解;
(L 5)存在算子T0∈L+(Z,Y),使得点(x0,y0)为问题(USOP)的ε-Henig有效对;




5 结 语
讨论了实局部凸Hausdorff拓扑向量空间中一类具约束集值向量均衡问题近似有效解的最优条件。在近似锥-次类凸基本假设下,运用凸集分离定理,结合相应的分析方法,得到了集值向量均衡问题的Henig近似有效解和Global近似有效解的Kuhn-Tucker型和Lagrange型最优条件,推广了文献[1,9,18]中的相关结论。

