半无限柱形区域中相互作用的Fochheimer流与Darcy流的空间衰减估计
欧阳柏平,李远飞
(广州华商学院数据科学学院,广东广州511300)
0 引 言
Saint-Venant原理指出,如果流入管道或通道无限端的净流量在任何时间均为零,当距离由有限趋于无限时,流速也趋于零。早期的Saint-Venant原理主要集中于有关椭圆方程的边值问题。1956年,BOLEY[1]首先指出Saint-Venant原理对热方程的重要性,并对抛物方程进行了广泛研究。Saint-Venant原理相关进展可参见文献[2]。
近年来,有关多孔介质模型方程解的性态研究备受关注,研究主要集中于Brinkman,Darcy,Forchheimer和Brinkman-Forchheimer等方程,以及多孔介质中模型解的性态。文献[3-4]以单方程组为研究对象,研究其空间衰减估计。实际上,同一区域中可能存在2个或多个方程,且这些方程之间存在相互作用,导致研究难度增加。AMES等[5]研究了在合适的界面条件下相互作用的多孔介质方程组与黏性流体方程组解的加权能量函数的指数衰减估计,得到了空间衰减估计结果。除该研究外,基本无文献涉及同一区域中2种或多种相互作用的流体方程组解的空间衰减估计研究。也有一些文献考虑了Brinkman,Darcy类方程组的结构稳定性,如文献[6-7]研究了Brinkman-Forchheimer方程组的结构稳定性;文献[8]通过添加溶解度,得到了结构稳定性的相关结果。但上述研究仅考虑有界区域中单个方程组的结构稳定性。文献[9-10]讨论了2个相互作用方程组的结构稳定性。受这些文献的启发,本文继续研究2个相互作用方程组解的空间衰减估计,将有界区域推广至无界区域。因无界区域对压力项的处理较困难,为此,较文献[5]增加了非线性项b|u|ui,由于非线性项的处理更复杂,此时,文献[5]的二阶微分不等式方法不再适用,须采用新的方法解决此问题。因此,如何处理非线性项是本文的重点和特色。其他关于Darcy,Forchheimer和Brinkman-Forchheimer方程的研究参见文献[11-15]。
设Ω=Ω1∪Ω2表示半无限柱体的内部,母轴线平行于x3,x1x3平面以上部分,即x2>0部分用Ω1表示,x1x3平面以下部分,即x2<0部分用Ω2表示,L表示Ω1和Ω2的交界面。在平面x3=0上,Ω1是有界的,其侧面用Γ1表示。同样,在平面x3=0上,Ω2是有界的,其侧面用Γ2表示。定义

其中,D1和D2分别表示Ω1和Ω2的横截面。由此可得,在Ω1中,x2>0;在Ω2中,x2<0。假设流体在Ω1中由依赖于温度的Forchheimer流体方程控制,在Ω2中由依赖于温度的Darcy流体方程控制。设(ui,T,p)和(vi,S,q)分别表示Ω1×{t>0}和Ω2×{t>0}上的流速、温度、压强,则Ω1×{t>0}上多孔介质的Forchheimer流体方程组为[4]
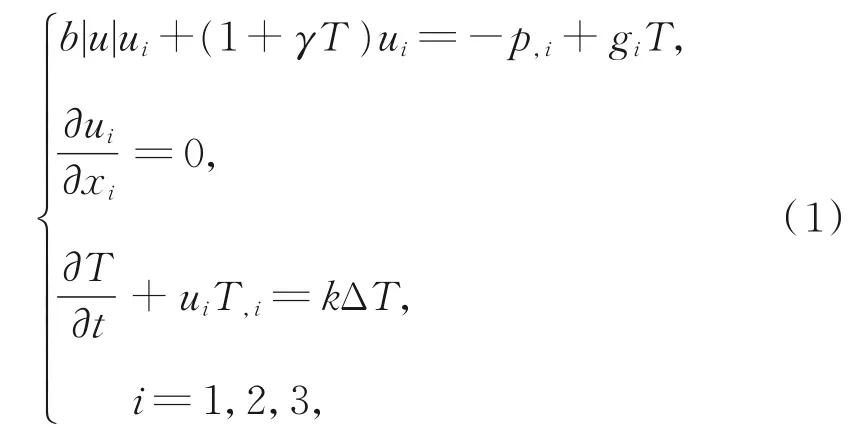
其中,b,γ为正常数,gi表示引力场,k表示流体(1)的热扩散系数。不失一般性,假设|g|≤1,则Ω2×{t>0}上多孔介质的Darcy流体方程组为

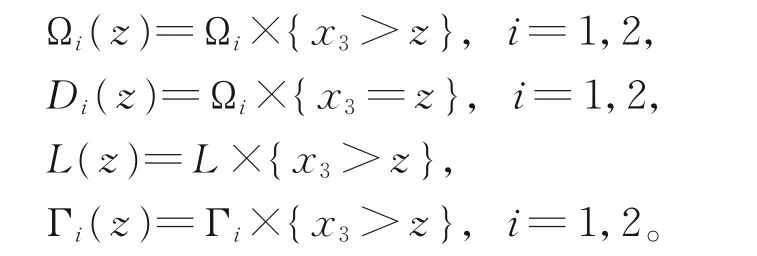
本文的目的是构造加权能量表达式,得到一阶偏微分不等式,最终得到解的空间指数衰减估计。
本文中,逗号表示求偏导数,下标,k表示对xk求偏导数,如u,k表示重复英文下标表示从1到3求和,重复希腊文下标表示从1到2求和。例如,

1 加权的能量表达式

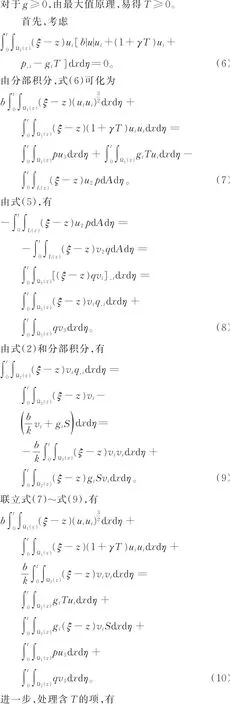


2 空间衰减估计



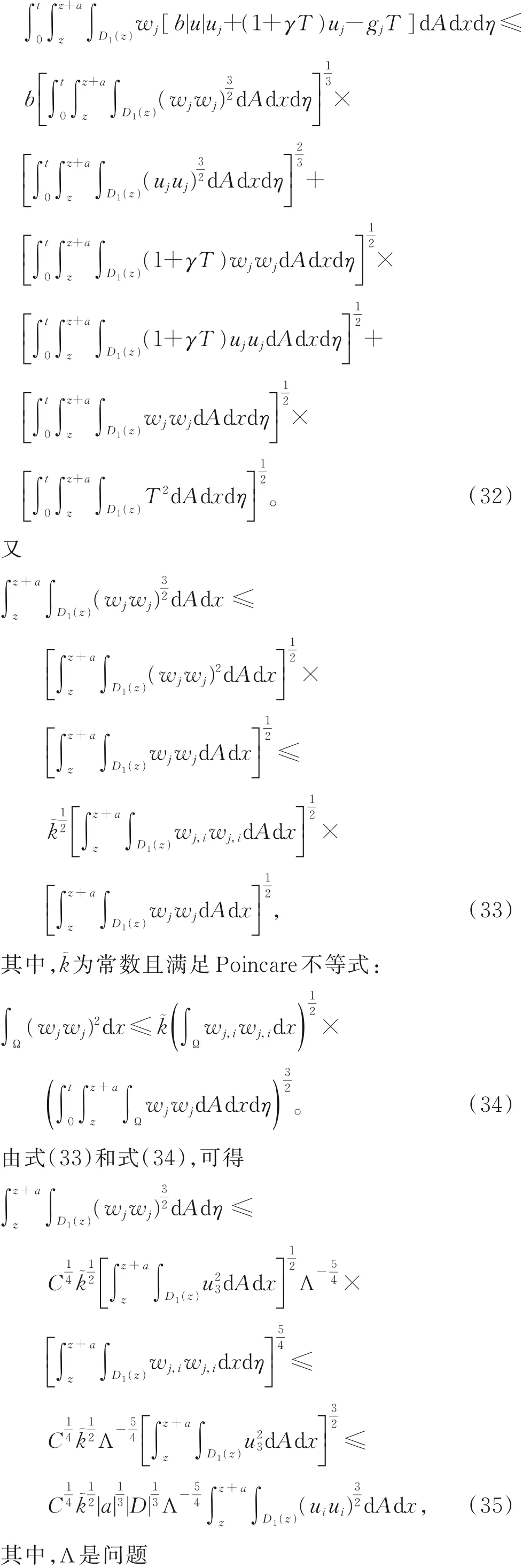



研究了多孔介质中二类相互作用的流体方程组解的空间性态,得到解的空间衰减估计。证明Saint-Venant原理适用于相互作用的流体方程组,且所用方法也适用于Darcy,Forchheimer和Brinkman-Forchheimer方程组。后续可继续研究无界区域解的性态,尝试将Forchheimer方程换成Navier-Stokes方程。由于Navier-Stokes方程的非线性项更复杂,构造的微分不等式会出现能量的非线性次方,如何求解该不等式是一大难点,有待后续进一步研究。

