基于改进型单相αβ-dq法的电网故障快速辨识技术研究

孙海洋 宋飞 王俊辉 侯凯

摘 要：對电网故障的快速辨识是电压补偿装置等电力设备性能保障的关键前提。在分析当前常用的电网故障辨识方法的基础上，重点研究了基于瞬时无功理论的辨识方法。对比了基于此理论的三相dq变换辨识法、单相dq变换辨识法和单相αβ-dq变换辨识法，为进一步提高辨识速度，提出了改进型单相αβ-dq变换辨识法，并进行仿真对比，结果验证了该改进方法的有效性及快速性。

关键词：电网故障辨识;瞬时无功理论;单相αβ-dq变换法;快速性

0    引言

在当前的配电网中，电网故障给负载供电及电力设备带来了巨大影响，因此，电压补偿装置及不间断供电等电力设备受到广泛关注，而快速辨识电网故障是诸多电力补偿设备实现电压有效补偿的前提与关键环节。

目前，电压识别方法主要有峰值电压法、基波分量法、小波变换法、dq变换法等[1]。

峰值电压法通过计算电压的采样点斜率，寻找出电压峰值点，然后判断该点是否与参考给定值一致便可辨识出电网是否故障。该方法简便、容易操作，但会受到外部信号干扰，且要半个周波才能辨识出。

基波分量法使用FFT对电压基波分量进行计算，同样需要至少半个周波的数据，且无法准确反映相位跳变情况，这在辨识快速性与准确性上都不能满足要求。

小波变换法以傅里叶分析为基础，可以有效分析信号中的变化量，具有良好的消噪能力。但如何选取合适的小基波还不够成熟，选取不当很可能导致辨识结果错误，且该方法实现起来比较复杂。

基于瞬时无功理论的辨识方法是目前常用的方法，其不需要历史数据即可获得电压幅值与角度[2]。

本文重点对比研究了三相dq变换辨识法、单相dq变换辨识法和单相αβ-dq变换辨识法，为进一步提高辨识速度，提出了改进型单相αβ-dq变换辨识法，并通过仿真验证了该改进方法的有效性及快速性。

1    三相dq变换辨识法

基于瞬时无功理论，三相dq变换辨识法将三相静止坐标系下abc电压通过Park变换变换到dq旋转坐标系下，进而获得电压幅值与相角[3]。三相电压可表达如下：

式中：U0、φ0分别为各相基波电压的有效值和初始相位;Un、φn分别为各相谐波电压的有效值和初始相位。

Park变换后可得：

Ud

Uq=Cua

ub

uc                            （2）

其中，变换矩阵C为：

C= cos ωt   cos（ωt-2π/3）  cos（ωt+2π/3）

-sin ωt  -sin（ωt-2π/3）  -sin（ωt+2π/3）

经过低通滤波器后可得：

Ud=

U0cos φ0，

Uq=-

U0sin φ0                   （3）

进而可得到电压幅值和相角：

U0=

，

φ0=arctan-

（4）

该方法只适用于三相系统，在实际系统中，多数情况是单相网压故障，因此这种方法就不适合了。

2    单相dq变换辨识法

对于单相电网故障，若想采用基于瞬时无功理论的dq法来辨识，可利用单相电压构造出一个虚拟的三相电压，假设a相电压发生故障，可以ua为参考电压，将ua延时60°即可得到-uc，进而得到ub=-ua-uc。由此方法可得到构造出的三相电压为：

ua=

U0sin（ωt+φ0）+

∑Unsin（nωt+φn），

ub=-

U0sin（ωt+φ0）-

∑Unsin（nωt+φn）+

U0sin（ωt+φ0-π/3）+

∑Unsin（nωt+φn-π/3），

uc=-

U0sin（ωt+φ0-π/3）-

∑Unsin（nωt+φn-π/3）（5）

将该三相电压dq变换并经过低通滤波器后同样可得：

Ud=

U0cos φ0，

Uq=-

U0sin φ0               （6）

进而可得到电压幅值和相角。

该方法通过虚拟出三相系统，可实现单相电压故障辨识，其实质上还是三相变换，计算量较大且实时性不是很好。

3    单相αβ-dq变换辨识法

单相αβ-dq变换法，其主要思想是根据单相电压由αβ静止坐标系变换到dq旋转坐标系[4]。αβ静止坐标系和dq旋转坐标系的转换关系如图1所示。

αβ与dq之间的转换公式为：

Ud

Uq= cos ωt  sin ωt

-sin ωt  cos ωtuα

uβ                    （7）

根据实测单相电压来构造αβ坐标系时，令实测单相电压为αβ坐标系中的uβ，并将超前uβ分量90°的电压作为uα，以a相电压为例，则有：

uβ=

U0sin（ωt+φ0）+

∑Unsin（nωt+φn），

uα=

U0sin（ωt-π/2+φ0）+

∑Unsin（nωt-π/2+φn）（8）

根据式（7）进行变换并经过低通滤波器后可得：

Ud=

U0cos φ0，

Uq=

U0sin φ0                 （9）

进而可得到电压幅值和相角为：

U0=

，

φ0=arctan

（10）

单相αβ-dq变换辨识法的优化之处是将单相dq变换法需要构建三相电压改进为只需构建两相电压，改进后，单相αβ-dq变换辨识法既能精确测定电压故障引发的相位跳变与幅值变化，又能显著缩减计算量。

4    改进型单相αβ-dq变换辨识法

如上文所述，单相αβ-dq变换辨识法可准确获得电压故障时的相位与幅值信息，但存在90°的时间延时，在检测快速性上存在固有不足，因此本文提出了改进型单相αβ-dq变换法，即将获取的单相电压延时一个可变小角度，构建新的uα，进而获取电压幅值与相位[5]。改进型单相αβ-dq变换辨识法结构图如图2所示。

同样以a相电压为例，把实测单相电压u1作为uβ，则有：

uβ=u1=U0sin（ωt+φ0）+∑Unsin（nωt+φn）    （11）

将u1延时一个小角度θ得到uθ，即：

uθ=U0sin（ωt+φ0-θ）+∑Unsin（nωt+φn-θ）   （12）

分解uθ可得：

uθ=U0sin（ωt+φ0）cos θ-U0cos（ωt+φ0）sin θ+

∑Unsin（nωt+φn）cos θ-∑Uncos（nωt+φn）sin θ （13）則：

uα=U0cos（ωt+φ0）+∑Uncos（nωt+φn）

= -                          （14）

将uα与uβ根据式（7）进行坐标变换并经过低通滤波器后同样可得：

Ud=

U0cos φ0，

Uq=

U0sin φ0                       （15）

进而可通过式（10）计算出电压幅值和相角。

5    仿真验证

为了验证改进后的单相αβ-dq变换法辨识电网故障效果，本文在Matlab/Simulink下搭建了仿真模型，并与未改进的单相αβ-dq变换辨识法进行比较。仿真参数为：网压峰值为311 V，频率为50 Hz，改进型单相αβ-dq变换辨识法中延时小角度选取为30°。0.05 s时电网电压幅值发生50%跌落，同时相位发生60°跳变;0.1 s时电网恢复正常。电网波形如图3所示。

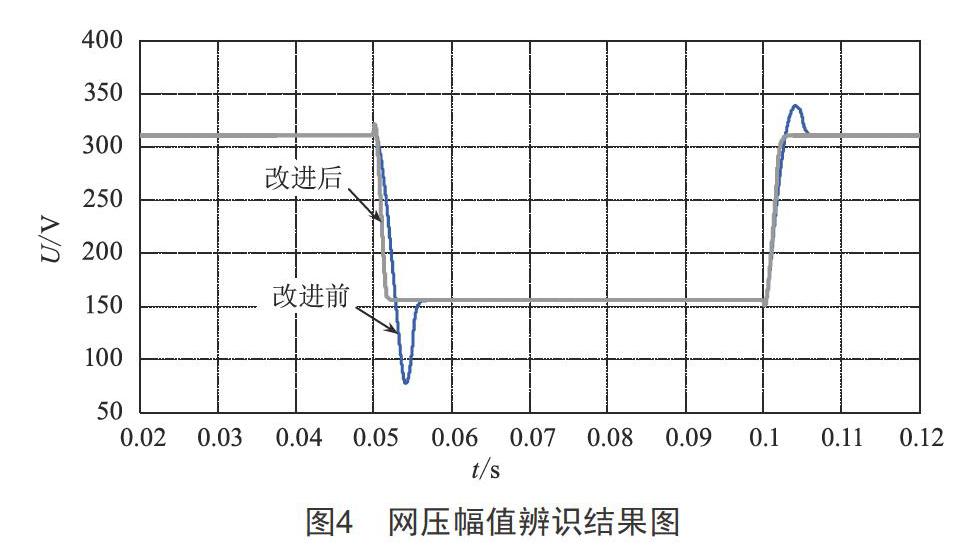
改进前与改进后的电网电压幅值辨识结果如图4所示。

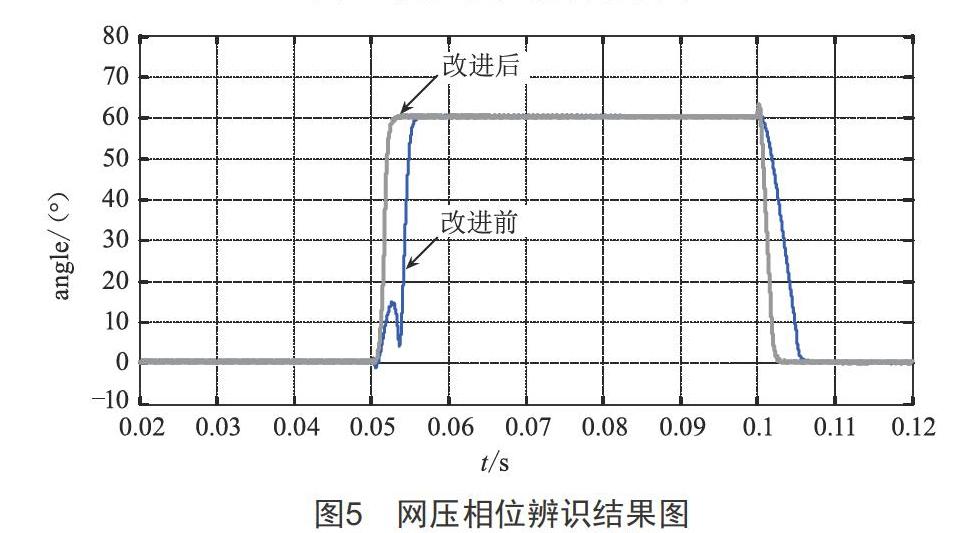
改进前与改进后的电网电压相位辨识结果如图5所示。

如图4和图5所示，两种方法虽然都能获取最终的电网电压幅值与相位，但采用未改进的单相αβ-dq变换辨识法需要5 ms才能完成判断;而采用小角度延迟的改进型单相αβ-dq变换辨识法只需要1.6 ms即可完成幅值与相位的准确辨识，提高了电网故障辨识的快速性，这对于电压补偿装置及不间断供电设备等电网故障治理装置的快速辨识与投入运行起到了关键作用。

6    结语

本文主要针对电网故障辨识方法进行了研究，分析对比了常用的三相dq变换辨识法、单相dq变换辨识法和单相αβ-dq变换辨识法。为满足电网故障辨识的快速性，提出了改进型单相αβ-dq变换辨识法，并进行仿真验证，对比结果表明了该改进方法的有效性与快速性。

[参考文献]

[1] 肖湘宁，徐永海，刘昊.电压凹陷特征量检测算法研究[J].电力自动化设备，2002，22（1）：19-22.

[2] 刘云潺，黄纯，欧立权，等.基于dq变换的三相不平衡电压暂降检测方法[J].电力系统及其自动化学报，2007，19（3）：72-76.

[3] 瞿硕，黄纯，江亚群，等.DVR电压暂降检测新方法[J].电工技术学报，2013，28（4）：234-239.

[4] 杨亚飞，颜湘武，娄尧林.一种新的电压骤降特征量检测方法[J].电力系统自动化，2004，28（2）：41-44.

[5] 许伟梁，施火泉，童庆国.一种适用于单相电压的改进电压暂降检测算法[J].电子测量与仪器学报，2017，31（6）：961-967.

收稿日期：2021-03-29

作者简介：孙海洋（1990—），男，江苏南京人，硕士，工程师，研究方向：电力电子技术、储能技术等。