基于积分数学-地质模型定量评价伸展断层侧向封闭性
吕延防,胡欣蕾,金凤鸣,肖敦清,罗佳智,蒲秀刚,姜文亚,董雄英
(1.东北石油大学地球科学学院,黑龙江大庆 163318;2.中国石油大港油田公司,天津 300280;3.中国石油大庆油田公司第四采油厂,黑龙江大庆 163511)
0 引言
根据断层断距和被错断砂、泥岩层厚度的相对大小,可将断层侧向封闭类型分为两种,即对接型封闭和断层岩型封闭。当断层断距小于其所错断单砂体厚度导致断裂带结构不发育、或断裂带孔渗性优于围岩时,研究目的盘储集层与对置盘非渗透性岩层对接,断层侧向封闭,该封闭类型为对接型封闭。当断层断距大于其所错断单砂体厚度时,岩层被彻底断开,研究目的盘储集层中运移到断层附近的油气能否被封挡,则取决于断层岩的封闭能力,这种封闭类型为断层岩型封闭[1-2]。
关于断层岩型封闭的伸展断层侧向封闭性的定量研究,归纳起来有3种方法:①泥质含量计算法,包括“SSF”法[3]、“CSP”法[4]和“CCR”法[5],均是通过计算断层裂缝中泥岩涂抹程度间接半定量评价断层封闭性,多适用于特定的地质环境。②“SGR”[6]法,通过计算断层岩泥质含量,结合对已知断层圈闭油气藏的压力统计,建立断层岩泥质含量与烃柱高度之间的数学统计关系式,达到定量评价断层侧向封闭性的目的[7-9]。该方法虽然是目前地质学家广泛应用的断层侧向封闭性评价方法,但其仍存在以下 3点不足:未从封闭机理出发,仅具有统计学意义,断层封闭能力与SGR值并不总呈正比关系;未考虑断层倾角,且对成岩程度(断点埋深)考虑过于粗略;资料均来自现存油气藏,建立的评价公式仅适用于有效断圈封闭烃柱高度的预测,对无效圈闭必将形成误判。③断-储排替压力差法,通过计算断层岩和储集层岩石排替压力并比较二者差值分析断层侧向封闭性[10-11]。在上述 3种伸展断层封闭性评价方法中,唯第3种断-储排替压力差法是基于断层封闭机理建立的定量评价方法,用已知断层圈闭所封闭的烃柱高度对3种方法进行验证时,断-储排替压力差法评价结果最接近实际[11]。因此,基于国内外断层封闭性研究现状,对断-储排替压力差法定量评价伸展断层侧向封闭性的深入研究与完善既有意义又有必要。
伸展断层封闭性评价的断-储排替压力差法最初是用于计算断点处断层岩承受的断面正压力和断层岩的泥质含量,考虑到具有相同泥质含量和承受相同静岩压力的岩石具有相同的成岩程度。因此,在具有相同排替压力的假设条件下,计算与断层岩相同泥质含量和所承受相同静岩压力的沉积地层岩石的排替压力,此排替压力即为该断点处断层岩的排替压力,以此排替压力与研究目的盘储集层排替压力相减,负值表明断层开启,正值表明断层封闭,且差值越大,断层封闭能力越强[10]。随着研究的深入发现,虽然断层岩和沉积地层目前具有相同的泥质含量和相同的成岩压力,但因断层岩和沉积地层所经历的成岩时间不同,致使二者的成岩程度不同,所以排替压力也就不同,二者简单的类比给实际伸展断层封闭性评价造成了很大误差,于是便提出了考虑成岩时间的伸展断层封闭性评价方法[11]。尽管该方法提高了断层封闭性评价的精度,但由于其将断层停止活动后上覆沉积地层视为一个整体,并没有考虑不同埋藏深度地层沉积速率的差异性,以及断层岩所受压力是随成岩时间增加逐渐累积的量值,这些必然导致伸展断层封闭性的评价结果与实际之间仍存在较大差异,且断层停止活动时间越早,评价结果与实际差值越大;另外,该方法还忽略了地应力在成岩过程中的作用。据此,本文以断-储排替压力差法研究为基础,充分考虑断层封闭性形成演化过程,建立了积分数学-地质模型,以期更准确地定量评价伸展断层的侧向封闭性。
1 伸展断层封闭性的形成与演化
断层一旦形成并活动,两盘间便形成裂缝[12],断层两盘的错动必然刮削两侧岩层形成碎屑并掉入断层裂缝中。断层活动形成的裂缝也是流体空腔,两盘渗透性地层孔隙水在地层压力差的作用下同时进入裂缝流体空腔,与断层裂缝中的碎屑混合形成未被压实的、且含有大量孔隙水的断裂充填物质。断层停止活动以后,断裂充填物质在垂向应力及水平地应力作用下逐渐排出孔隙水向断层岩转化[13]。与正常沉积地层相同,断裂充填物承受的成岩压力越大,所经历的成岩时间越长,断层岩的成岩程度越高,在相同泥质含量情况下,断层岩的排替压力越大。当断层岩的排替压力达到被封挡的目的盘储集层岩石的排替压力时,断层开始具备侧向封闭能力[14-15]。随着断层岩的不断深埋,成岩压力逐渐增大,所经历的承压时间逐渐累积,断层岩的成岩程度不断增强,断层岩排替压力也不断增大,断层封闭能力不断增强。
影响伸展断层岩排替压力的主要因素是断层岩的泥质含量和成岩程度,断层岩的成岩程度又取决于断层岩承受的垂向应力、水平地应力和成岩时间,垂向应力又受断点埋深和断层倾角的控制,断层倾角越小,断点埋深越大,则应力越大;水平地应力则受埋深、断层倾角及应力方向与断层走向夹角等因素控制[9,16-17]。
2 积分法定量计算伸展断层封闭性
以往对断层岩封闭能力的定量研究中,在考虑成岩时间对断层岩排替压力的影响时,往往把断层岩所经历的成岩时间和成岩压力分开来考虑[11],并没有认识到成岩压力与成岩时间之间的内在关系。实际上,随着成岩时间的增加,断点处断层岩的埋深逐渐增加,成岩压力也随之增大,即成岩压力是随着成岩时间增加而不断增大的变量。在长期的成岩过程中,断层岩所受的成岩作用实际上是一个压力累积的过程。为此,本文以砂泥岩地层、伸展断层为研究目标,用成岩压力在所研究地质时期内对成岩时间的积分计算断层岩的成岩程度,以期更准确地评价断层岩的侧向封闭能力。
2.1 断层岩泥质含量的求取
断层岩是断裂充填物发生成岩作用的产物,断裂充填物又是由于断裂活动使得断层两盘砂泥岩地层被刮削成碎屑,与地层水共同进入断层裂缝中形成的,故断层岩中的泥质成分来源于两侧砂泥岩地层,其含量主要与被错断围岩层的砂泥岩层层数、厚度及断层断距大小有关。可以用Yielding所提出的公式求取[6]:

2.2 岩石排替压力的求取
根据前人的研究,岩石的排替压力与岩石的泥质含量与埋深的乘积存在明显的正相关关系[16],岩石的泥质含量越高,埋藏深度越大,排替压力越大。故在求取岩石排替压力时,可以选取研究区的典型岩石样品,通过实测数据建立岩石排替压力与泥质含量和埋深二者乘积的拟合统计公式:

2.3 积分法定量计算断层岩排替压力的数学-地质模型
当伸展断层处于活动期时,上下断盘相互研磨,滑动削截的围岩碎屑物质落入断裂带,此时断裂充填物并未发生成岩作用;当断层活动停止后,断裂填充物便在上覆沉积载荷及水平地应力的作用下,逐渐排出孔隙水并缓慢成岩,即断层岩真正开始发生成岩作用是在断层停止活动之后,对应图1中③号地层开始沉积时期。
首先,假设断裂带内的物质组成和结构与围岩地层中的岩石相同(基于以下两点考虑:安全因素,钻遇到断层可能会出现井喷或跳钻等现象;局限性,钻遇断裂带的井位相对较少,且断层岩易碎较难获取到实验所需岩样,受井位分布的影响不具有全区代表性),借助于围岩排替压力间接研究断层岩排替压力。在图1中,研究断点A的排替压力,如果围岩中存在一点K,K点岩石的泥质含量和成岩程度与A点断层岩的泥质含量和成岩程度相同((3)式、(4)式),那么K点就具有与A点相等的排替压力,其中成岩程度为成岩压力与成岩时间的函数[10-11,17],受垂向应力及水平地应力共同影响。本文将用断层岩所受的断面正压力及水平地应力在所研究成岩时间范围内的积分值来表示。

图1 积分法计算断层岩排替压力地质模型
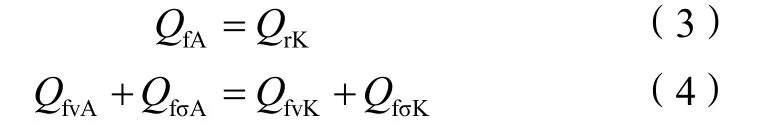
2.3.1 断层岩成岩程度的确定
2.3.1.1 垂向应力对断层岩成岩程度的贡献
如图1所示,断裂带内断点A处的碎屑填充物在t3时开始成岩,根据 A点的埋深及上覆①、②、③号地层的平均沉积速率v1、v2、v3,确定其上覆地层沉积厚度,即A点埋深与成岩时间的关系:
断点A处断面的正压力与断点A的埋深存在如下关系:

联立(5)式及(6)式,便可以得到断面正压力与成岩时间的函数关系,二者间的积分值即可表征垂向应力对断层岩成岩程度的贡献(见图2、(7)式)。若研究区地层存在明显的抬升剥蚀,可将(7)式进一步完善为(8)式所表述形式。
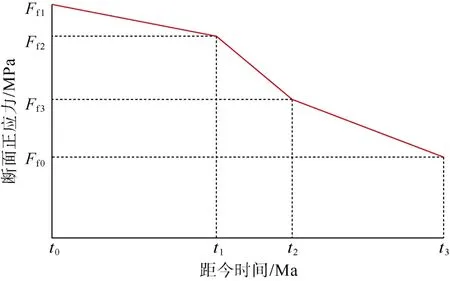
图2 断层岩垂向应力成岩程度积分数学模型

2.3.1.2 水平地应力对断层岩成岩程度的贡献
断层岩在成岩过程中,除了受到上覆沉积载荷作用在断面上的垂向应力影响外,还要受到水平地应力的控制。1978年Brown和Hoek总结归纳了世界不同地区垂向地应力随埋藏深度的变化规律((9)式)[18],结合中国沉积岩石平均水平地应力与垂向地应力间关系((10)式)[19],便可求得岩层所受水平地应力。同时,综合考虑不同地质时期地应力大小及方向特征,建立(11)式所示的断层岩水平地应力成岩程度积分数学-地质模型。

2.3.1.3 断层岩成岩程度的确定
将垂向应力和水平地应力分别对断层岩成岩程度的贡献进行累加,便可确定自断层停止活动后断层岩的成岩程度。
2.3.2 断层岩排替压力的确定
2.3.2.1 垂向应力对围岩成岩程度的贡献
如图1所示,在围岩层中根据每一沉积地层的平均沉积速率,可分别得到以不同围岩地层为初始沉积地层开始沉积,沉积至t0(现今)时,上覆岩层厚度即K点埋深与沉积时间的数量关系,以下(12)—(15)式分别对应K点位于①—④号地层内的情况:
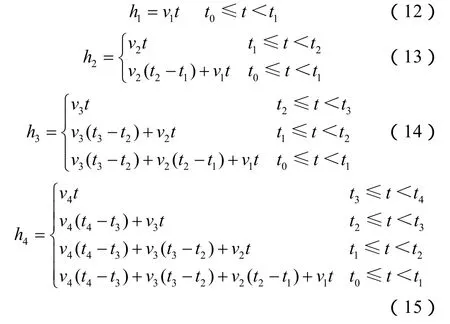
地层所受上覆地层静压力的大小与地层的埋深具有如下关系:

将(12)—(15)式代入到(16)式中,便可得到:

联合上述公式即可得到地层所受静岩压力与沉积时间之间的函数关系(见图3),通过上覆地层静岩压力对沉积时间的积分可计算不同围岩地层在垂向应力作用下的成岩程度((21)—(24)式):
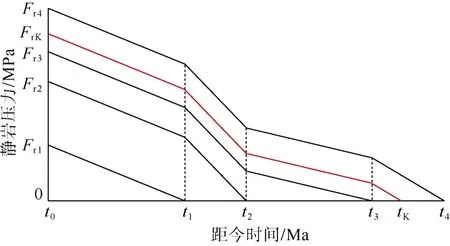
图3 围岩垂向应力成岩程度积分数学模型

2.3.2.2 水平地应力对围岩成岩程度的贡献
基于上述水平地应力对断层岩成岩程度贡献的分析,建立不同围岩地层在水平地应力作用下具有的成岩程度:

2.3.2.3 围岩成岩程度的确定
将垂向应力和水平地应力分别对不同围岩地层成岩程度的贡献进行累加,便可确定以任意层为初始沉积层时围岩的成岩程度。
2.3.2.4 断层岩排替压力的确定
根据(8)式、(11)式即可得到A点断层岩的成岩程度,在围岩地层中存在一点K,使得K点的岩石成岩程度与A点断层岩的成岩程度相等((3)式)。
通过对(16)—(28)式对应层垂向应力及水平地应力成岩程度的累加,可得到任意一点围岩地层的成岩程度。假设A点的成岩程度介于③、④号围岩层底界面对应的成岩程度之间,即Qr3<QfA<Qr4,便可确定与A点断层岩具有相同成岩程度的K点位于④号地层中,根据(24)式及(28)式可得:

在确定K点沉积至今时间tK的基础上,根据④号地层的平均沉积速率即可得到K点的埋深(该埋深表现为研究目标断层岩A考虑成岩时间对成岩压力作用效果后得到的具有成岩意义的压实成岩埋深),由于K点的泥质含量与A点的泥质含量相同,K点的埋深又已知,根据(2)式便可计算得到K点的排替压力,即为A点断层岩的排替压力。
以上便是利用积分数学-地质模型计算断层岩排替压力的过程,应该特别指出的是,(3)—(29)式在考虑垂向成岩压力对成岩时间的积分过程时,虽然其中成岩压力是利用岩石所受压实成岩压力表征的,但成岩时间并非只是单纯地代表断层岩或储集层岩石所经历的成岩时间,而是在这段时间内岩石所经历的所有成岩作用因素的综合。除此之外,在建立(2)式所示的岩石排替压力拟合公式时,研究区典型岩样是实际经历过地下机械压实,以及胶结、溶蚀等多种成岩作用的综合影响。综合上述两方面考虑,该模型是符合地下岩石在地质历史时期经历多种成岩作用综合影响的实际地质情况的,而并非仅考虑了机械压实作用,只是将所有成岩作用对断层岩或储集层岩石的影响均反映在其成岩埋深上,即对应前文与研究目标点断层岩A具有相同成岩程度围岩K的埋深,该数值具有的地质意义包括压实特征,但绝不局限于压实特征。
2.4 储集层岩石排替压力的求取
根据伸展断层附近典型井的自然伽马曲线,即可获得储集层岩石泥质含量的变化规律[17],结合目的盘储集层岩石的埋深,将其代入研究区所建立的岩石排替压力与泥质含量和埋深函数关系式((2)式),便可求取储集层岩石的排替压力。
2.5 伸展断层侧向封闭性定量评价
比较上述确定的断层岩排替压力与研究目的盘储集层岩石排替压力的相对大小,如果断层岩排替压力小于储集层岩石排替压力,断层不具备侧向封闭能力;如果断层岩排替压力大于等于储集层岩石排替压力,断层侧向封闭,二者间差值越大,断层侧向封闭能力越强。封闭能力的大小可用所能封闭的烃柱高度表示[10]:
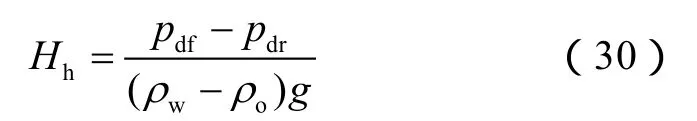
值得注意的是,上述积分数学-地质模型的建立是基于“断裂带内的物质组成和结构与围岩地层中的岩石相同”这一假设,但是在一般情况下断层岩较围岩更容易受到胶结作用的影响。如果研究区胶结作用发育程度相对较弱,那么该方法在评价伸展断层侧向封闭性时更接近于地下实际情况;如果研究区胶结作用发育程度极强,那么评价结果表征了伸展断层所具有的最小封闭能力,该值对于实际油田开发则是最安全的数值。但是,无论针对哪种地质情况,该方法在评价伸展断层侧向封闭性时均是适用的。
3 应用实例
本文以渤海湾盆地南堡凹陷 1号构造区内 F1、F2及F3断层圈闭为例,通过上述方法对断层的侧向封闭性进行评价,同时利用未考虑成岩时间和简单考虑成岩时间的断-储排替压力差法分别进行评价,将其与利用本方法得到的评价结果进行对比,结合实际分析本文研究方法的合理性。
3.1 区域地质概况
南堡 1号构造是渤海湾盆地南堡凹陷内最主要的油气富集区之一,其位于南堡凹陷西南部斜坡带,受中国东部新生代裂陷盆地北西—南东向(距今 40 Ma以前)及近南北向(距今40 Ma以后)两期伸展构造作用影响[20],表现为一在潜山背景下发育的有大量伸展断层分布的披覆背斜构造,呈北东走向[21-23](见图4)。该区的沉积地层由下至上发育古近系沙河街组(Es)、东营组(Ed)、新近系馆陶组(Ng)、明化镇组(Nm)以及第四系(Q),其中沙河街组二、三段(简称沙二、沙三段)和沙河街组一段(简称沙一段)—东营组三段(简称东三段)是南堡凹陷主要的生油气层,东营组二段(简称东二段)泥岩层为良好的区域性盖层[24]。岩心测试及实地测量等多种手段均揭示,南堡1号构造在地质历史时期地应力状态发生2次转换,现今最大主应力方向以近东西向为主[25]。根据流体包裹体均一温度和井埋藏史研究表明,该区油气充注时间是距今24.6~25.5 Ma和距今6.0~9.5 Ma,分别对应东营组沉积末期和明化镇组沉积中期[26]。

图4 南堡凹陷1号构造F1断层明化镇底面构造图
前人研究成果揭示[27],南堡凹陷埋深小于3 100 m和大于3 500 m时岩石所受成岩作用以机械压实作用为主,3 100~3 500 m埋深的岩石则以方解石胶结作用为主,目前南堡 1号构造东营组一段(简称东一段)—第四系埋藏深度均小于3 100 m,表明上述层位内岩石发生胶结作用的概率较小。除此之外,研究区测井解释成果亦揭示了典型井孔隙度随埋深呈指数规律变化,尚未出现明显的孔隙度增大或减小区段[28],也表明该地区岩石主要受机械压实作用影响,胶结作用发生的概率较小。因此,可利用上述建立的积分数学-地质模型定量评价伸展断层的侧向封闭性及封闭能力。
3.2 典型伸展断层F1侧向封闭性评价
F1断层是南堡 1号构造内一条重要的遮挡断层,延伸长度约为2.3 km,断距为20~200 m,断层倾角为40°~60°(见图5),与倾斜地层构成断层圈闭,该圈闭油源供给、储集层物性等成藏要素匹配良好[28],故油气能否在圈闭内聚集成藏主要取决于断层的侧向封闭与否。且该圈闭目前在浅层——明化镇组—馆陶组钻遇油气,断层岩埋藏较浅,以发生机械压实作用为主,满足上述方法的假设条件。因此,选择南堡 1号构造F1断层作为典型伸展断层,以验证本文建立的积分数学-地质模型在定量评价伸展断层侧向封闭性时的合理性与准确性。
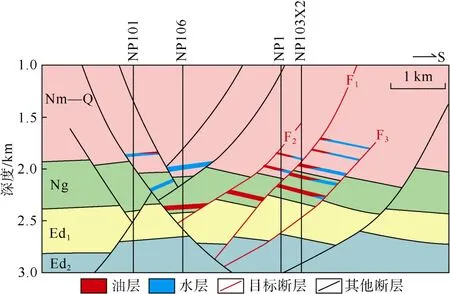
图5 过F1、F2及F3断层油藏剖面图(剖面位置见图4)
①断层岩泥质含量的确定。依据研究区三维地震解释成果,建立断层-地层构造地质模型,结合F1断层附近典型井的测井曲线数据,明确围岩地层泥质含量随埋藏深度的变化规律,再依据(1)式计算F1断层在三维空间上任意一点的断层岩泥质含量(见图6)。结果表明,F1断层在明化镇组—东一段下部断层岩泥质含量相对较高,除断层中东部局部地区在馆陶组SGR值低于20%以外,其与部位均大于25%,局部甚至高达70%。

图6 南堡1号构造F1断层SGR属性图
②岩石排替压力的求取。在研究区不同层位、不同深度钻取规格为2.5 cm×1 cm(直径×高)的典型岩石样品34块,结合各岩样的埋藏深度及泥质含量(可利用测井曲线求得或利用X衍射法测量得到),便可建立岩石排替压力与其埋藏及泥质含量间乘积的函数关系(见图7),三者间具有较好的指数关系,对应的拟合关系式为(31)式。因此,在明确岩石泥质含量及埋藏深度的基础上,可依据下式确定相应岩石的排替压力值:
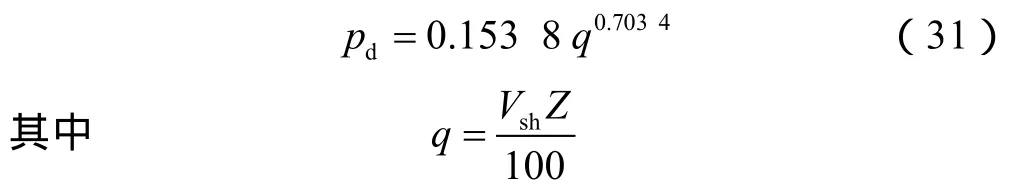

图7 南堡1号构造岩石排替压力与埋深、泥质含量间关系
③断层岩成岩程度的确定。根据三维地震解释成果,F1断层在明化镇组沉积末期活动停止,表明断层岩所经历的成岩时间为明化镇组末期至今时间段,约为2.58 Ma。按照上文提出的积分法计算步骤,根据F1断层最后停止活动时间和研究目的断点 A处的埋深、岩石骨架密度(见图8),以及依据地层沉积时间和沉积厚度等资料得到的不同沉积速率(其中,平原组为791 m/Ma、明化镇组为23 m/Ma、馆陶组为53 m/Ma、东营组为194 m/Ma、沙一段为798 m/Ma、沙二段为600 m/Ma、沙三段为75 m/Ma)。便可在明确南堡1号构造地层沉降史的基础上,利用(5)—(8)式及(9)—(11)式分别计算得到A点断层岩的垂向应力成岩程度及水平地应力成岩程度。
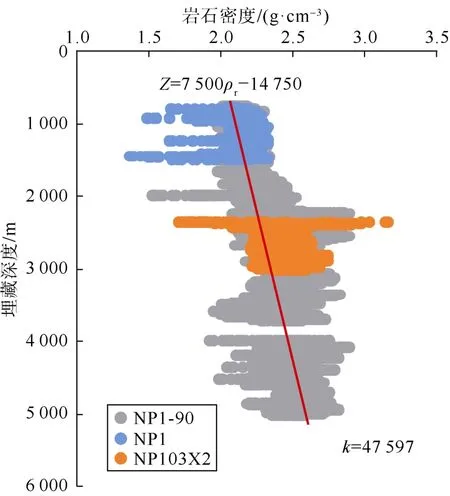
图8 南堡1号构造岩石密度随埋藏深度的变化规律
④断层岩排替压力的确定。首先,根据各层的平均沉积速度、沉积时间及地应力特征,分别利用(12)—(24)式和(25)—(28)式计算沉积地层中以任意层为初始沉积层对应的垂向应力成岩程度和水平地应力成岩程度,将二者累加确定围岩层成岩程度。然后,通过比较上述确定的目标点断层岩成岩程度与不同围岩层成岩程度间关系,利用(3)式及(29)式确定与A点具有相同泥质含量和相同成岩程度的围岩层中K点所在层位及埋深,该埋深即为目标断层岩A的压实成岩埋深;其中,与NP103X2井内①—⑤号储集层岩石相对置的断层岩压实成岩埋深为 958~1 399 m。再结合上述确定的A点断层岩SGR值,依据(31)式计算K点地层岩石的排替压力;由于K点排替压力与A点排替压力相等,此排替压力即为断点A的排替压力,为0.61~0.84 MPa(见表1)。
⑤储集层岩石排替压力的求取。根据与A点对置的储集层岩石的埋深和泥质含量,利用研究区实际资料建立的排替压力拟合关系式((31)式)计算储集层岩石的排替压力。
⑥F1伸展断层侧向封闭性定量评价。将断层岩和储集层岩石在各点排替压力差的最小值作为断层的封闭能力,并利用(30)式计算出断层各点所能封闭的油气柱高度,为70~165 m(见表1)。由表1可知,研究目的盘储集层岩石的排替压力为0.51~0.63 MPa,利用本文方法计算得到F1断层在不同埋深处的断层岩排替压力值为0.61~0.84 MPa,二者间的断-储排替压力差值为0.09~0.21 MPa,评价值均大于0,表明研究目标点断层岩均具有一定封闭能力,可遮挡油气并形成油气聚集。结合研究区地层中的原油密度,利用本文方法建立的积分数学-地质模型预测得到的烃柱高度与实际烃柱高度十分接近,误差仅为0~3 m(见表1)。同理,重复上述伸展断层侧向封闭性定量评价流程,对南堡1号构造 F2及 F3断层进行分析(见图9),所得的评价结果分别与受上述断层封闭的 NP1及 NP1-90井的实际油气分布同样吻合较好,其中F2断层预测误差为0~3.8 m,F3断层预测误差为0.5~8.2 m,也进一步印证了本文方法对定量评价伸展断层侧向封闭性的可靠性。

图9 南堡1号构造NP1井、NP1-90井F2、F3断层侧向封闭性评价结果及封闭油柱高度
将利用未考虑成岩时间[10]和简单考虑成岩时间[11]方法计算的结果一同列入表1中,并同时与实际所封闭的烃柱高度进行对比分析,比较这两种研究方法及本文建立的积分数学-地质模型研究结果与实际资料的吻合关系。由评价结果可知(见表1),在利用未考虑成岩时间的断-储排替压力差法对 F1断层的封闭能力进行评价时,大大低估了断层的封闭能力,研究目的盘储集层5层中仅1层被封闭,封闭的油柱高度(20 m)远远低于实际被封闭的油柱高度(162 m),这表明在利用未考虑成岩时间的断-储排替压力差法评价伸展断层封闭性时,因忽略了成岩时间对成岩程度的影响而使断层实际封闭能力被低估,同时也揭示了成岩时间是影响断层岩成岩作用的重要因素。而在利用简单考虑成岩时间的断-储排替压力差法计算 F1断层的封闭能力时,计算结果与实际也存在较大偏差(见表1),这主要是由于在考虑成岩时间求取排替压力时,只是简单地将上覆地层沉积所经历的总时间作为断层岩和沉积地层的成岩时间。实际上,上覆地层每层的沉积时间是不同的,某一薄地层沉积所经历的时间可能比另一厚地层沉积所经历的时间长,而薄地层和厚地层施加给下伏地层或断层岩的压力是不同的,如果地层的厚度差异很大,所经历的沉积时间范围差异也很大。尽管两地层总沉积时间一定,但二者对下伏地层成岩程度的贡献差异却很大,造成下伏地层的成岩程度在此一定时间内因上覆各地层的沉积速率不同而不同,由此计算得到的断层岩和储集层排替压力就不会准确,伸展断层封闭性的评价结果与实际必然存在偏差;且上覆各地层沉积速率差异越大,评价结果与实际的偏差就越大。实际上,上覆地层压力是随时间增长和地层不断加厚而不断增加的,岩石的成岩程度不是一个瞬时的量,而是一个随成岩时间的增长和地层加厚而不停累积的变量,所以通过成岩时间对成岩压力的积分再现断层岩经历的成岩过程,合理地考虑了成岩时间对成岩的影响,计算得到的封闭能力与实际情况十分接近。由此可见,本文提出积分数学-地质模型计算断层封闭能力更符合实际。
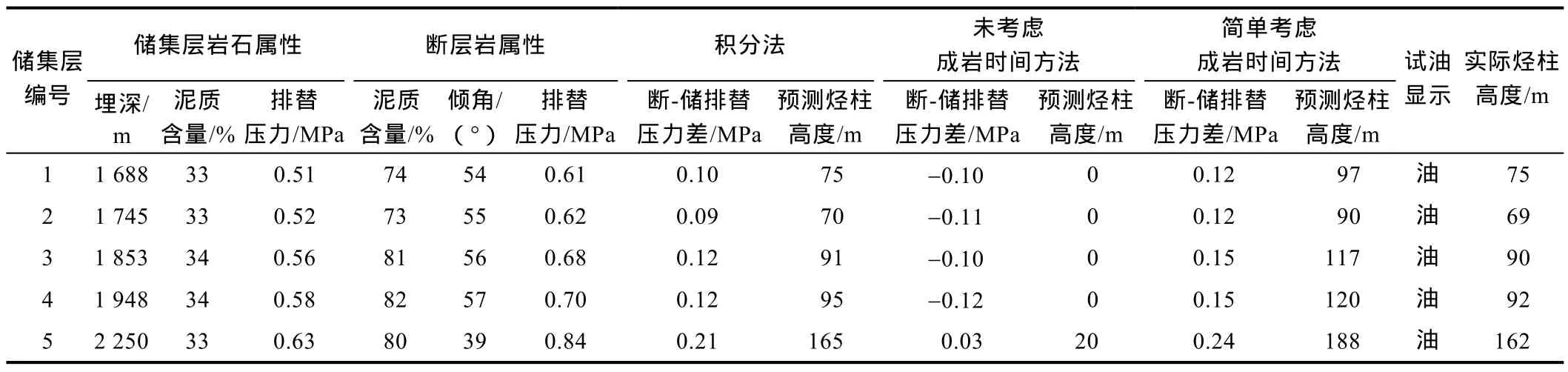
表1 南堡凹陷1号构造F1断层NP103X2井处侧向封闭性定量评价数据表
4 结论
断层自形成后受多种成岩作用影响,在形成侧向封闭性及封闭能力的过程中,考虑到目标断层岩所受成岩压力是随成岩时间和沉积地层厚度增大而不停累加的变量,即断层岩经历的成岩时间越长、承受的成岩压力越大,断层岩排替压力越大,伸展断层越容易形成侧向封闭。通过建立断层岩及围岩地层所受成岩压力随成岩时间变化的积分数学-地质模型来表征其成岩程度,便可依据与断层岩具有相同成岩程度的围岩埋深及断层岩泥质含量,借助研究区岩石排替压力拟合关系式确定断层岩排替压力,用储集层岩石排替压力与之比较,定量评价伸展断层的封闭性及封闭能力大小。南堡 1号构造内典型断层(F1、F2及 F3)评价结果表明,预测烃柱高度与实际钻探结果吻合程度较好,误差仅0~8 m,评价结果与地下实际情况吻合较好。
利用成岩时间对成岩压力的积分表征伸展断层侧向封闭性的数学-地质模型,是在“断裂带内的物质组成和结构与围岩地层中的岩石相同”的假设条件下建立的,考虑到在一般情况下断层岩较围岩更容易受到胶结作用的影响。基于此提出积分数学-地质模型评价伸展断层侧向封闭性时的适用条件,即为待评价区块研究目的层位未发生胶结作用,此时得到的伸展断层侧向封闭性定量评价结果更符合地下实际。但这并不意味着发生胶结作用的地区不能用该积分数学-地质模型评价伸展断层的侧向封闭性,只是此时得到的评价结果为断层所具有的最小封闭能力,胶结作用的发生必然会使封闭能力进一步增大,该值则是实际油田开发保持伸展断层封闭的最安全数值。
有关伸展断层侧向封闭性的研究,目前较难获取到足够多、且具有整条断裂带甚至全区可代表性的断层岩岩样进行直接分析,仅能通过围岩地层来间接评价伸展断层的侧向封闭性。但是这样的评价方法仍存在诸多亟待解决的难点问题,如断层岩的非均质性(溶蚀及胶结作用发育程度的差异)、实测数据如何与积分数学-地质模型结合等问题,故有关伸展断层侧向封闭性的定量评价仍需进一步研究。
符号注释:
Ffab——已剥蚀ab段地层在未剥蚀前作用在A点的断面正应力,Pa;Ffi——ZAi厚度的上覆岩层作用在 A点的断面正应力,Pa;FrK——K 点围岩所受的上覆静岩压力,Pa;Fr——围岩上覆静岩压力,Pa;g——重力加速度,m/s2;h1——①号地层底界面至地表距离,m;h2——②号地层底界面至地表距离,m;h3——③号地层底界面至地表距离,m;h4——④号地层底界面至地表距离,m;hK——K点至地表距离,m;Hh——断层面某点所能封闭的烃柱高度,m;H——断层垂直断距,m;k——样品数;m1——①号地层沉积时期内经历的地应力期次;m2——①~②号地层沉积时期内经历的地应力期次;m3——①~③号地层沉积时期内经历的地应力期次;m4——①~④号地层沉积时期内经历的地应力期次;m——岩石开始成岩至今经历的地应力期次(可根据地应力大小及方向划分);n——滑过断点的围岩层层数;pdf——断层岩排替压力,MPa;pdr——储集层岩石排替压力,MPa;pd——岩石样品的排替压力,MPa;QfA——A点断层岩成岩程度,Pa·Ma;QfvA——垂向应力对A点成岩程度的贡献,Pa·Ma;QfσA——水平地应力对A点成岩程度的贡献,Pa·Ma;QrK——K点围岩成岩程度,Pa·Ma;Qrv1——①号地层在垂向应力下具有的成岩程度,Ma;Qrv2——①~②号地层在垂向应力下具有的成岩程度,Ma;Qrv3——①~③号地层在垂向应力下具有的成岩程度,Ma;Qrv4——①~④号地层在垂向应力下具有的成岩程度,Ma;QrvK——垂向应力对K点成岩程度的贡献,Pa·Ma;Qrσ1——①号地层在水平地应力下具有的成岩程度,Ma;Qrσ2——①~②号地层在水平地应力下具有的成岩程度,Ma;Qrσ3——①~③号地层在水平地应力下具有的成岩程度,Ma;Qrσ4——①~④号地层在水平地应力下具有的成岩程度,Ma;QrσK——水平地应力对K点成岩程度的贡献,Pa·Ma;q——泥质含量与垂直距离之积,m;SGR——断层岩泥质含量,%;t0——现今沉积时间,Ma;t1——①号地层初始沉积时间,Ma;t2——②号地层初始沉积时间,Ma;t3——③号地层初始沉积时间,Ma;ta——地层抬升剥蚀初始时间,Ma;tb——地层抬升剥蚀结束时间,Ma;tjs——岩层经历的第j期次地应力起始时间,Ma;tjf——岩层经历的第j期次地应力结束时间,Ma;tK——K点围岩沉积至今的时间,Ma;t——地层沉积时间,Ma;v1——①号地层的平均沉积速率,m/Ma;v2——②号地层的平均沉积速率,m/Ma;v3——③号地层的平均沉积速率,m/Ma;Vshi——滑过断点的第i层岩层泥质含量,%;Vsh——岩石样品的泥质含量,%;Z0——A点与④号地层顶界面之间的垂直距离,m;Z1——A点与③号地层顶界面之间的垂直距离,m;Z2——A点与②号地层顶界面之间的垂直距离,m;Z3——A点与①号地层顶界面之间的垂直距离,m;ZA——断点A的埋深,m;ZAi——A点断层岩上覆地层的沉积厚度,m;Z——岩石埋深,m;γ——水平地应力方向与断层走向夹角,(°);ΔZi——滑过断点的第i层岩层厚度,m;θ——断层倾角,(°);ρo——烃密度,kg/m3;ρr——上覆沉积岩层骨架密度,kg/m3;ρw——地层水密度,kg/m3;σhj——岩层经历的第j期次水平地应力大小,Pa;σhmax——最大水平地应力,Pa;σhmin——最小水平地应力,Pa;σh——水平地应力,Pa;σv——垂向地应力,Pa。
——以北部湾盆地福山凹陷为例
——以加拿大麦凯河油砂储集层为例

