基于高效求矩法与最大熵原理的矩方法
姜昊锐,赵衍刚
(北京工业大学城市建设学部,北京 100124)
工程结构在使用过程中存在着诸如材料参数、几何参数以及外部荷载作用等不确定性,日益引发了人们对基于概率设计的重视,结构可靠度分析在结构设计与使用过程中起到越来越重要的作用[1]。目前常用的可靠度分析方法有蒙特卡洛模拟法[2]、一次二阶矩法(first order reliability method, FORM)[3-5]与二次二阶矩法(second order reliability method, SORM)[6-8]等,但蒙特卡洛模拟方法在处理小失效概率问题时需要大量的计算,效率低下;FORM与SORM因为需要计算导数以及迭代运算,在处理复杂工程问题时精度较低。矩方法也是可靠性分析方法之一,因其方法简单,便于操作而受到越来越多的重视。矩方法具体包含两个步骤:首先求解功能函数的统计矩,如前四阶中心矩:均值,标准差,偏度,峰度;接着依据求得的统计矩信息,选择合适的分布模型近似真实的概率分布,最终在失效域上进行积分求解结构的失效概率与可靠指标。由上述步骤可知,矩方法不需要像蒙特卡洛模拟法进行大量运算,也无需像FORM或SORM一样计算导数以及迭代运算,但求矩的效率与精度直接影响着矩方法的精度与效率[7-9],如何高效且准确地求解功能函数的矩,目前仍旧是矩方法所研究的重点。
求解功能函数的统计矩,实质上就是计算多维积分。在实际工程中,由于结构的功能函数通常较为复杂且以隐式函数表示,直接进行多维积分运算往往较为困难[10]。因此,许多近似计算方法相继被提出。Zhao等[11]提出了新点估计方法,通过Rosenblatt变换[12]和一维减维方法[13]将功能函数表示成一元函数和的形式,继而用一维点估计进行求矩运算,很大程度上提高了计算的效率,但该方法在功能函数较为复杂的情况下计算精度较低。为了提高计算精度,Zhao等[14]提出了将Rosenblatt变换和二维减维方法[15]相结合的二维减维点估计方法,将功能函数表示成一元函数与二元函数和的形式进行求矩运算,但随着输入随机变量数目的增加,该方法往往会造成“维数灾难”问题。Xu等[16]提出了用高阶无迹变换[17-19]计算二维减维点估计中的二维积分问题,该求矩方法可一定程度上提高计算精度与效率。为了进一步提高计算的效率,Fan等[20]提出了自适应二维减维点估计方法,通过引入交叉项判定准则,判断二维减维后的二元函数中是否存在交叉项,若不存在交叉项,则将二元函数进一步用一元函数表示,并用一维点估计法进行求矩运算;若存在交叉项,则用二维点估计进行计算,但在功能函数所含交叉项较多的情况下,该方法依旧需要大量的运算。针对此问题,Cai等[21]提出采用二维稀疏网格法[22]计算自适应二维减维点估计方法中的二维积分,可一定程度上提高计算效率,但在输入随机变量数目较多的情况下计算量依旧较大。综上所述,已有的求矩方法均不能在计算过程中兼顾精度与效率。
鉴于此,现提出一种基于快速求矩法与最大熵原理的矩方法,将自适应二维减维与高阶无迹变换相结合求解结构功能函数的前四阶矩,并选择最大熵原理[11]近似真实的概率分布,最终依据最大熵分布求解结构的可靠指标。算例部分通过两道例题,对比所提方法与几种已有方法的计算结果,验证所提方法在求矩运算以及可靠指标计算问题中在效率以及精度上的优势。
1 基于矩方法的可靠度分析
1.1 问题表述
结构的功能函数[5]的表达式通常为
Z=G(X)
(1)
式(1)中:Z为功能函数;X=[X1,X2,…,Xn]为n维随机向量,功能函数的前四阶中心矩计算公式为
μG=μ1G
(2)
(3)
(4)
(5)
式中:μG、σG、α3G和α4G分别为功能函数的均值、标准差、偏度与峰度;μkG为功能函数的k阶原点矩(k=1,2,3,4),具体计算表达式为

(6)
式(6)中:fx(x)为输入随机向量的联合概率密度函数。由式(6)可知,求矩运算本质上是多维积分计算问题,但实际工程中功能函数较为复杂,且随机向量的联合概率密度函数难以直接获得,因此直接求解并不可行。为了高效且精确地求矩,提出基于自适应二维减维与高阶无迹变换的高效求矩法。
1.2 自适应二维减维
结构可靠性分析一般在标准正态空间下进行,因此可通过Rosenblatt变换或者Nataf变换[23],将输入的具有相关性的非正态随机变量转换为独立的标准正态随机变量U=[U1,U2,…,Un],此时功能函数可用标准正态随机变量[18]表示为
Z=G(X)=G[T-1(U)]=L(U)
(7)
式(7)中:T-1为Rosenblatt逆变换或Nataf逆变换;L为G与T-1的复合函数。
基于二维减维[12]方法,功能函数可进一步写为
(8)
式(8)中:L2为n(n-1)/2个二元函数的和;L1为n个一元函数的和;L0为功能函数在均值点处的函数值,为一常数。L2、L1、L0的具体表达式为
(9)
(10)
L0=L(0,…,0,…,0)
(11)
式中:i,j=1,2,…,n,i 基于式(8)~式(11)可得,功能函数在二维减维后的k阶原点矩的近似计算表达式为 (12) (13) (14) 式中:φ(u)为标准正态随机变量的概率密度函数。由式(14)易知求解μk-Li为一维积分问题,可通过一维点估计法[15]进行计算,即 (15) 式(15)中:ur为积分点;Pr为对应权重;N为积分点个数。一维点估计中积分点及其对应权重的计算式[16]为 (16) (17) 式中:xr、ωr分别为以exp(-x2)为权函数的2N-1阶高斯埃尔米特积分的积分点与权重值[24]。 式(13)中含有两个随机变量,为二维积分问题,文献[21]采用二维点估计进行运算,即 (18) 针对此情况,自适应二维减维点估计方法[17]提出了交叉项判定准则,通过判定准则判断函数中是否存在交叉项,将判定为不含有交叉项的二元函数进一步用一元函数表示,对应的矩的计算可直接利用一维积分的计算结果;判定为存在交叉项的二元函数,其矩仍通过二维点估计进行计算。 判断二元函数中是否存在交叉项的具体步骤如下。 (1)首先选取参考点Ur=(uir,uir),并带入功能函数计算,用Lij(Ur)表示。 (2)另选取3个参考点,分别记为Ui-1=(ui-1,ujr),Uj-1=(uir,uj-1)以及Uij-1=(ui-1,uj-1),代入式(19)计算Δ1,即 (19) 若Δ1>ε,则可判定在二元函数Lij(Ui,Uj)中Ui,Uj存在交叉项,否则执行下一步。 (3)再选取3个计算点,分别记为Ui-2=(ui-2,ujr),Uj-2=(uir,uj-2)以及Uij-2=(ui-2,uj-2),代入式(20)计算Δ2,即 (20) 若Δ2>ε,则可判定在二维函数Lij(Ui,Uj)中Ui,Uj存在交叉项,否则Lij(Ui,Uj)中Ui,Uj不存在交叉项。 在上述步骤中ε为一特定值,作为判别交叉项存在的标准,取ε=10-6。值得注意的是,交叉项判定选取的计算点通常是进行一维点估计计算的积分点,因此不需额外增加计算量。 如果二维函数Lij(Ui,Uj)经上述判别准则判定为不存在交叉项时,则二元函数可用一元函数表示为 Lij(Ui,Uj)=Li(Ui)+Lj(Uj)-L0 (21) 继而不含交叉项的二元函数矩的求解,可直接利用一元函数Li(Ui)、Lj(Uj)矩的计算结果进行计算,即 μ1-Lij=μ1-Li+μ1-Lj-L0 (22) (23) (24) (25) 式中:M2ij、M3ij、M4ij计算表达式分别为 (26) (27) (28) 由式(22)~式(28)可知,此时二维积分计算可直接利用一维积分计算结果,无需额外增加计算量,因此一定程度上提高了求矩的效率。 若判定二元函数中存在交叉项,则采用二维点估计进行计算,为保证精度通常采用5点或7点估计,此时每个二元函数的求矩过程分别需计算25次或49次功能函数值。在交叉项较多的情况下,进行二维点估计求矩的二元函数数目较多,因此仍旧需要大量的运算。针对此情况,通过采用高阶无迹变换方法替换原有的二维点估计,减少了二维积分中积分点的个数,相应减少了功能函数的计算次数,一定程度上提高了求矩的计算效率。 高阶无迹变换可以用于解决n维高斯权重积分问题[21]。高阶无迹变换的基本思想是[18]:首先,选取一些特定的积分点(Sigma点)及其对应的权重来匹配输入随机变量的概率信息,通常为输入随机变量的各阶统计矩;其次,将选取的积分点通过非线性变换,即带入结构的功能函数计算对应的输出状态变量的样本点;最后,输出状态变量的统计矩可以利用输入变量的积分点对应权重和输出状态变量的样本点进行估计,其实质上为一种改进的高斯积分。 由前述可知,高阶无迹变换积分点总个数为N=2n2+1,在自适应二维减维后的二维积分问题中,n=2,则每个二元函数矩的计算仅需9次运算,其效率明显高于二维点估计中的5点或7点估计。 高阶无迹变换三类积分点及其对应权重的具体表达式[13,15]如下。 第一类: θ0=0 (29) (30) 第二类: (31) (32) (33) 式中:ej1=[0,…,1,…,0],即只有第j1项为1。 第三类: (34) (35) (36) (37) (38) 在计算第二类和第三类积分点时,需要引入自由参数β,其影响着高阶无迹变换的计算结果的精度,文献[16,18]中对β的取值进行过研究,在此取β=7.2,经不同例题试算结果表明,所选取的β值计算结果精度较高。 当自由参数确定后,三类积分点及权重由式(29)~式(38)进行计算,此时含有交叉项的二元函数的矩可直接由式(39)进行计算,即 (39) 式(39)中:ωi、θi分别为高阶无迹变换积分点与对应权重,i=1,2,…,n。 最后,将计算所得的自适应二维减维后的一元函数、二元函数的矩代入式(12)中,功能函数的前四阶原点矩μkG即可确定(k=1,2,3,4),继而可通过式(2)~式(5)计算功能函数G(X)的前四阶中心矩。 获得功能函数的前四阶中心矩后,需选择合适的分布模型对功能函数的真实概率分布进行近似,并以此计算结构可靠指标。常用的分布模型有Pearson分布族、Burr分布族等,尽管该类分布系统非常灵活,但在不同分布类型的分界处往往难以实现分布近似。因此,采用最大熵原理近似结构功能函数的概率分布,避免了上述问题,同时该分布模型对真实概率分布的拟合效果较好,且分布参数计算方便。 若功能函数Z服从概率密度函数为fZ(z)的连续分布,其熵定义[25-26]为 (40) 根据最大熵原理可知,最大熵分布为所有可能的分布形式中,在给定约束条件下,使熵最大的概率分布,其具有最小偏见,因此被认为是构造“最优”概率分布的一种途径。 为使式(40)的熵取最大值,此处以计算的功能函数前四阶原点矩为约束条件。在计算最大熵分布时,为求解方便,提高收敛速度,通常先将功能函数进行标准化处理为 (41) 此时对功能函数Z的分布近似转变为对标准化变量Y的概率分布的近似。 最大熵分布的求解可通过引入拉格朗日算法[26]进行计算,表达式为 (42) 令式(42)关于拉格朗日乘子的偏导数为0,即 (43) (44) 利用所得到的最大熵分布,在失效域上积分可计算得到结构的失效概率为 (45) 对应的结构可靠度指标计算公式[3]为 β=Φ-1(1-pf) (46) 式(46)中:Φ-1为标准高斯随机变量的累计分布函数的逆函数。 综上,以自适应二维减维与高阶无迹变换求得的功能函数前四阶矩为约束条件,结合最大熵原理,最终便可计算得到结构的可靠指标。 所提出的一种新的矩方法,基于自适应二维减维与高阶无迹变换高效求解功能函数的前四阶中心矩,并采用最大熵原理求解结构的可靠指标。具体计算步骤如下。 (1)根据式(8)将结构功能函数进行二维减维,表示成二元函数与一元函数和的形式。 (2)一元函数的矩直接通过式(15)的一维点估计进行运算求解。 (3)引入交叉项判定准则:①通过准则判定为不含有交叉项的二元函数,利用式(21)进一步用一元函数表示,其对应的矩可利用已求得的一元函数矩的结果直接进行计算;②判定为含有交叉项的二元函数,其矩采用高阶无迹变换方法进行计算。 (4)将求得的一元函数、二元函数的矩的计算结果代入式(12)中,即可计算功能函数的前四阶原点矩,继而由式(2)~式(4)计算前四阶中心矩。 (5)以计算得到的前四阶中心矩为约束条件,基于最大熵原理求解功能函数的最大熵分布,继而通过最大熵分布在失效域上的积分,可最终求解结构的失效概率与可靠指标。 为验证所提方法在计算精度与效率上的优势,选取两道算例,将所提高效求矩方法计算得到的功能函数前四阶中心矩结果,与蒙特卡洛模拟方法、一维减维点估计方法、二维减维点估计方法、自适应二维减维点估计、二维减维无迹变换及自适应二维减维稀疏网格积分方法进行了对比。此外,将基于最大熵原理计算得到的可靠指标与蒙特卡洛方法结果进行了对比。 某根受轴向压力的环形柱,其受力图与平面几何尺寸如图1所示,其中环形柱的弹性模量为E,长度为L,内径为D,壁厚为T,受到轴向荷载P的作用。其中,E、L、D、T、P为相互独立的随机变量,具体对应的概率分布及分布参数如表1所示。 图1 轴向压力环形柱示意图 表1 各随机变量的分布信息 此处受轴向压力环形柱的失效模式为屈曲破坏,其对应的极限状态函数表达式为 (47) 表2中分别列出了蒙特卡洛模拟方法,一维减维点估计方法、二维减维点估计方法,自适应二维减维点估计,二维减维无迹变换及自适应二维减维稀疏网格积分方法的求矩结果与计算次数。同时以蒙特卡洛模拟法结果为标准,不同方法计算结果的相对误差也在表内括号里列出。其中,相对误差计算公式为 (48) 式(48)中:e为相对误差;rMCS为蒙特卡洛模拟方法计算结果;r为各求矩方法计算结果。 由表2可知,一维减维点估计方法计算效率较高,但偏度与峰度的计算误差较大。所提求矩方法相较于其他方法,计算效率有一定程度的提升,仅需计算59次,且提高效率的同时,计算的精度也能保证,且误差更小。其中,本文方法计算得到的前四阶中心矩中偏度的相对误差最大,但仅有1.31%。 表2 各求矩方法计算结果 求解得到前四阶中心矩后,便可按照1.4节步骤计算对应的最大熵分布,继而进行可靠指标计算。表3中列出了本文方法结合最大熵分布计算得到的可靠指标结果,并与蒙特卡洛方法计算结果进行对比,以验证所求结果的精度。同样,采用式(12)计算本文方法计算得到的可靠指标相对于蒙特卡洛模拟方法结果的相对误差。 表3 可靠指标计算结果 从表3可知,本文方法求得的可靠指标与蒙特卡洛较为吻合,在保留三位有效数字情况下结果与蒙特卡洛方法结果基本一致,相对误差仅有0.7%。由此可知本文方法结合最大熵原理进行可靠指标计算时精度较高,符合误差范围。 如图2所示,有一个由72根杆件构成的空间桁架,其中各个杆件的横截面面积均为34.849 cm2,F1、F2、F3、F4、F5、F6、F7、F8分别为作用在节点5、8、9、12、13、16、17、20处的水平作用力,所有作用力与构成空间刚架的杆件的弹性模量E互为独立随机变量,对应的概率分布与分布参数如表4所示。 图2 空间72杆框架示意图 表4 各随机变量的分布信息 此处考虑该空间桁架的极限状态为所有节点的水平位移绝对值最大值超过界限值,该失效模式所对应的结构功能函数表达式为 Z=G(X)=0.05-max|μi(x)|,i=5,6,…,20 (49) 式(49)中:0.05为沿x方向水平位移限值,m。本例题计算过程中,空间桁架的各个节点水平位移通过MATLAB软件进行有限元分析计算。表5中列出了各个求矩方法计算得到的功能函数前四阶中心矩,同算例1,表中括号内也列出了各个求矩方法计算结果相较于蒙特卡洛模拟方法结果的相对误差。 在计算得到功能函数前四阶中心矩后,依据最大熵原理计算相应的结构可靠指标并与蒙特卡洛方法对比,具体结果如表6所示。 表6 可靠指标计算结果 由表5可知,在求解隐式功能函数(14)的前四阶中心矩时,本文方法计算功能函数次数较少,仅需计算211次功能函数值,且效率提升的同时也能保证计算的精度,其中本文方法计算得到的前四阶中心矩中峰度结果的相对误差最大,但也仅有3.9%。 表5 各求矩方法计算结果 最后通过最大熵分布拟合功能函数的分布函数并进行结构可靠度分析,计算得到该空间桁架的结构可靠指标为2.934,蒙特卡洛模拟法计算结果为3.051,相对误差为3.8%,可知本文方法在效率提升的同时能保证一定的精度。 提出了一种新的矩方法,基于自适应二维减维与高阶无迹变换进行高效求矩,并结合最大熵原理计算结构的可靠指标。通过算例部分的两道例题,对比了本文方法与既有方法的求矩结果以及可靠指标计算结果,最终能得到以下的结论。 (1)求矩方面,所提高效求矩方法在运算过程中,计算结构功能函数的次数少于其他求矩方法,因此在计算效率方面优于既有的求矩方法。通过不同的求矩结果与蒙特卡洛模拟方法结果的对比,可知所提求矩方法在提高效率的同时,在计算精度上也有明显优势,误差更小。 (2)可靠指标计算方面,通过结合高效求矩法与最大熵原理计算得到可靠指标,并与蒙特卡洛方法结果对比,可知所提矩方法计算的结构可靠指标与蒙特卡洛模拟方法的结果较为吻合,相对误差满足工程要求。



1.3 基于高阶无迹变换的二维积分算法


1.4 基于最大熵原理的可靠指标求解




1.4 算法步骤
2 算例分析
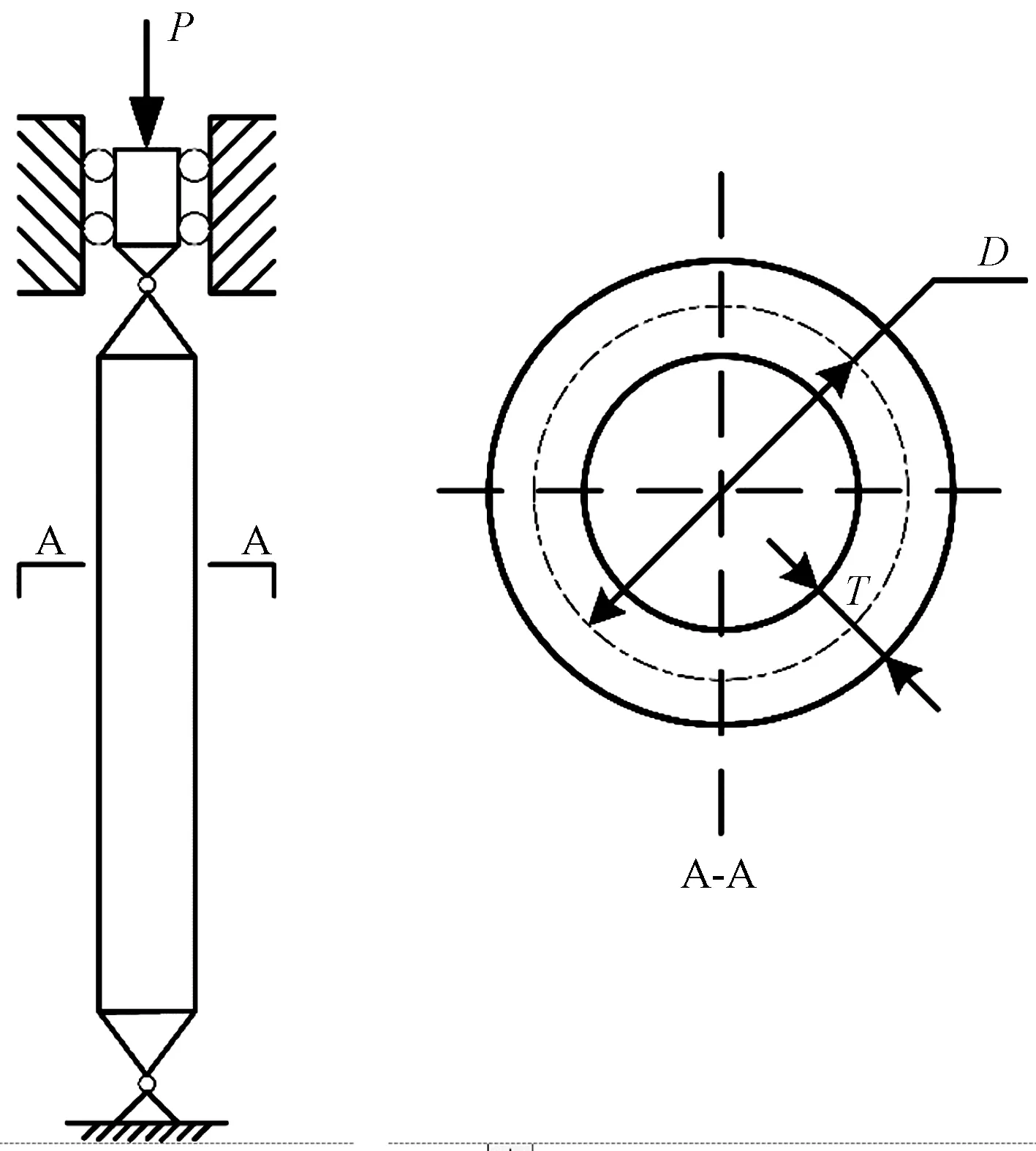
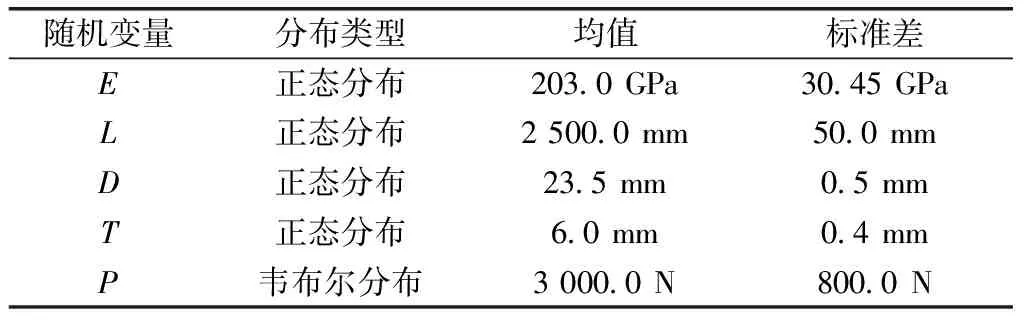
2.1 算例1:轴向压力环形柱可靠度分析


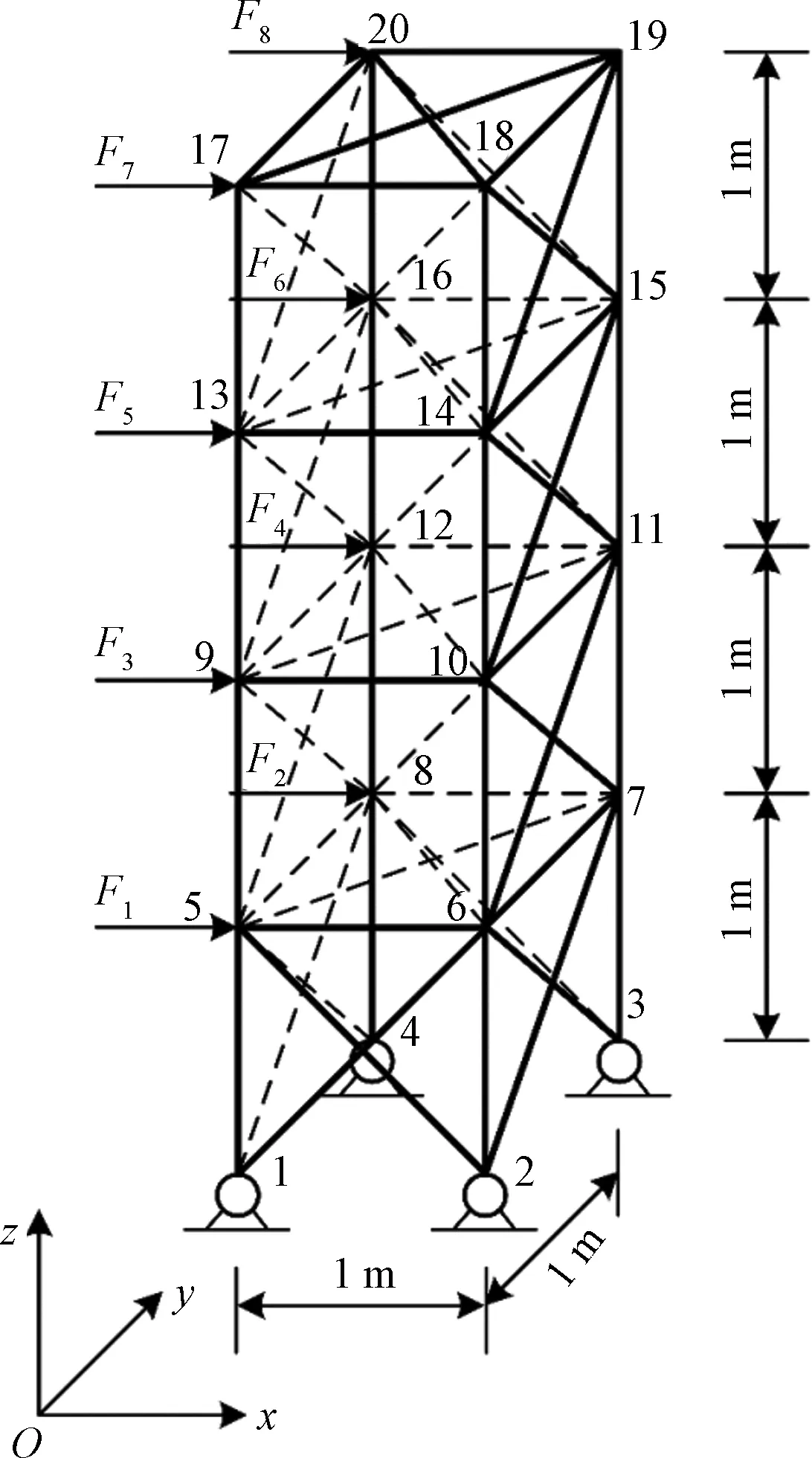
2.2 算例2:空间刚架可靠度分析



3 结论

