潮流能水轮机复合材料叶片的 损伤特性研究

余国庆，李秀海，陈文光，李军向，刘 清

（明阳智慧能源集团股份公司，中山 528437）

0 前言

由于全球面临能源危机、环境污染以及气候变暖等问题，世界各国正在把能源的发展投向绿色可持续能源领域。潮流能作为一种储藏量大的可再生清洁能源，具有较强的规律性和预测性，建设周期短，不存在移民问题等优势，在新能源开发领域具有一定的前景［1-5］。叶片是水轮机中潮流能转化为机械能的核心部件，其占整机成本的20%，直接影响水轮机的结构性能和水动力性能。水轮机叶片的早期设计主要参考风机，基于对设计以及制造工艺的考虑，叶片早期主要为钢制叶片。后期由于叶片大型化，水动力载荷随之加大，此外海洋环境复杂，对水轮机叶片提出了更高的要求。近些年来，复合材料技术的快速发展使得复合材料替代金属叶片成为可能，相比于金属材料，复合材料的比强度、比刚度、疲劳耐久等性能更加优越［6］，这使得复合材料在水轮机叶片设计领域成为研究重点。

叶片是水轮机设计的关键部件，国内外许多学者在水轮机叶片的力学分析与设计领域做了相关研究。Bir等人［7］采用层合板理论设计出了满足极限强度以及抗屈曲等要求的叶片，该方法充分考虑了沿叶片展向任意分布的弦长、扭角、翼型以及腹板。Liu等人［8］采用优化设计的方法设计出了满足结构强度的叶片，在满足叶片安全系数的前提下减轻叶片质量的37.6%。Grogan等人［9］结合流固耦合的设计理念设计出1.5MW的潮流能水轮机叶片。国内许多学者［10-12］也针对潮流能水轮机叶片结构提出了多种设计方法。

目前，国外许多学者对复合材料叶片的损伤展开了相关研究。Pawar等人［13，14］通过试验的方法研究了直升机复合材料叶片的同步损伤探测，并探讨了基体开裂对弯曲、扭转挠度以及叶根弯矩的影响，同时也研究了直升机复合材料叶片的冲击损伤。Tawk等人［15］通过建立冲击损伤模型来分析喷气式发动机材料叶片的鸟撞问题。Garcia等人［16］运用多变量统计方法评估风机叶片的损伤。Talreja等人［17］从3个时间阶段阐述了复合材料的损伤以及疲劳机理。Nanami［18］采用有限元仿真的方法分别评估了在气动载荷和冲击载荷工况下，大型碳玻混杂复合材料叶片的损伤。另一方面由于复合材料加工工艺缺陷以及铺层复杂多样性，复合材料的损伤机理并不成熟［19，20］。目前的损伤评估主要集中在航空发动机叶片和风机叶片，但是水轮机叶片的工况相比航空发动机和风机叶片复杂很多。水的密度是空气密度的800多倍，因此水轮机叶片承受的载荷要大很多。尽管在复合材料叶片的结构设计已经取得一些进展，但是在叶片损伤评估仍处于起步阶段，国内的相关研究工作仍处不足，因此急需开展相关研究。

本文以某型号潮流能复合材料水轮机叶片为研究对象，基于Tsai-Hill失效准则建立复合材料叶片损伤模型。针对正常运行工况利用叶素动量理论求出水动力载荷，然后评估叶片在该工况下的损伤特性。最后基于碳玻混杂技术，对可能出现失效的部位进行改进。通过对比分析碳玻混杂叶片的损伤特性，为进一步设计轻质高性能水轮机叶片提供了重要参考价值。

1 复合材料叶片结构

潮流能水轮机叶片主要是由外部蒙皮和内部主梁构成，蒙皮是由不同截面转动一定角度并放样的三维结构，其主要提供水动力性能并承载部分剪切力，而主梁则是主要承载部件，其形式多种多样，有箱型梁、工字梁以及D型梁等不同结构。工字梁叶片横截面如图1a所示。运用叶片的二维翼型坐标以及弦长扭角参数，坐标变换可以得到三维坐标，通过云点数据导入Catia软件即可得到叶片三维模型，如图1b所示。

图1 叶片结构

叶片的材料设计是叶片设计的重要环节，关系到整个叶片设计的成败。考虑到叶片的载荷和复合材料的工艺，以玻璃纤维增强树脂基复合材料作为叶片材料。叶片在运行过程中承受弯扭耦合，结合经典层合板理论，将蒙皮、梁帽和抗剪切腹板的铺层分别设计为[0°/90°/±45°] s、[0°] s，这样就使得蒙皮承受部分剪切，并有一定的刚度，梁帽承受主要的弯矩，腹板抵抗剪切。此外，夹层结构在尾缘和腹板的铺层设计中也得到应用，增强结构刚度，提高抗屈曲能力。

2 水动力载荷

水动力是叶片运行期间最重要的载荷。本文将运用叶素动量理论求出水动力载荷，升力阻力可通过以下方程计算：

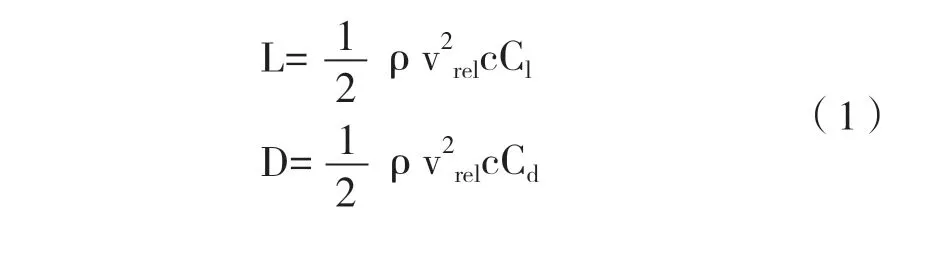
式中：

L ——单位长度的升力， N/m；

D ——单位长度的阻力， N/m；

ρ——水密度，kg/m3；

vrel——相对速度， m/s；

c ——弦长，m；

Cl——升力系数；

Cd——阻力系数。

再将升力和阻力沿叶轮平面分解，可得到切向力和法向力，分解如公式（2）所示

式中：

pN——单位长度的法向力， N/m；

pT——单位长度的切向力， N/m；

L ——单位长度的升力， N/m；

D ——单位长度的阻力， N/m；

φ——入流角，deg。

3 损伤模型

叶片根部连接到轮毂，应用最广泛的为螺栓连接，此连接方式属于刚性连接，所以将叶片简化为一根悬臂梁。载荷通过集中力的方式施加在参考点上，并在参考点通过MPC（Multi-points Coupling）多点耦合约束和叶片翼面建立联系。叶片采用S4R单元模拟，该单元是一种具有4结点的缩减积分单元。

针对所给的铺层，对复合材料叶片结构进行分析，经典层合板的本构方程为：

式中：

N——横截面上单位宽度（或长度）上的内力（拉力压力或剪切力）， N/m；

M——横截面上单位宽度（或长度）上的内力矩（弯矩或扭矩）， N；

A——拉伸刚度， N/m；

B——耦合刚度， N；

D——弯曲刚度，N·m；

ε0——中面应变；

K——中面曲率，m-1。

层合板的失效是一个逐层破坏过程，而单层复合材料的失效是研究层合板失效的基础。常用单层材料的强度理论主要有：最大应力理论、Tsai-Hill强度理论、Tsai-Wu张量理论。

本文采用Tsai-Hill强度理论对复合材料水轮机叶片进行强度失效分析。

Tsai-Hill强度理论：

式中：

F、G、H、L、M、N——各向异性材料的破坏强度参数， N/m2；

σ1——材料第1主方向的应力，Pa；

σ2——材料第2主方向的应力，Pa；

τ12——面内切应力， Pa；

σ3——材料厚度方向的应力，Pa；

τ13——13平面的切应力，Pa；

τ23——23平面的切应力，Pa

当公式（4）左边的数值达到1，表明该层合板失效，因此可以用该数值表征复合材料的损伤特性。

4 损伤特性分析

针对水轮机复合材料叶片，运用有限元对其结构分析并采用Tsai-Hill失效准则评估叶片损伤特性。针对某型号水轮机，其工况如表1所示。

表1 水轮机的性能参数

根据叶素动量理论可求得在该工况下，叶片的法向力和切向力分别如图2所示。

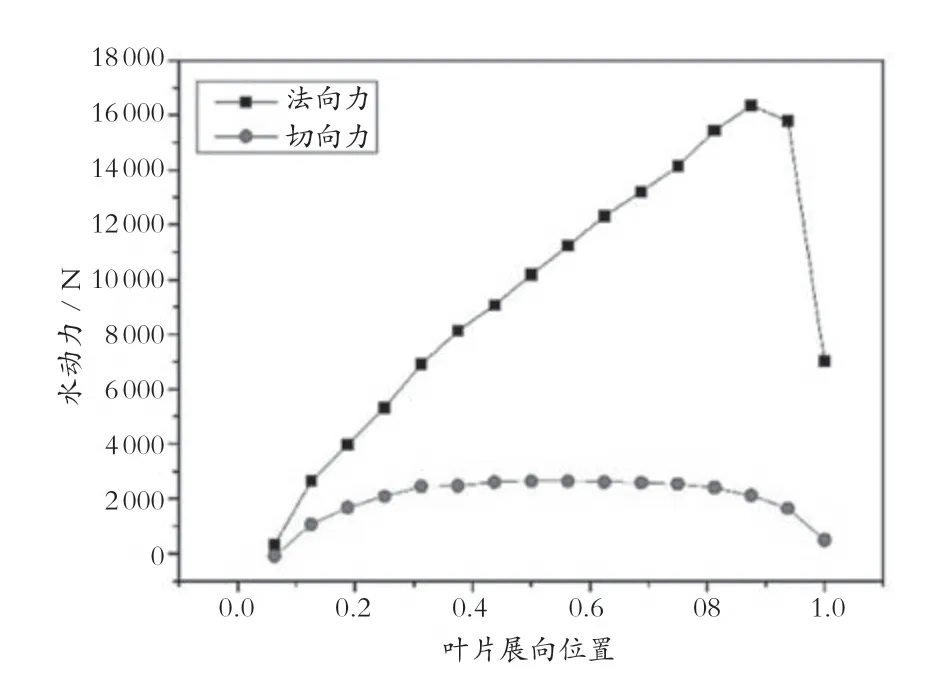
图2 叶片水动力载荷

4.1 原始叶片

针对给定的叶片模型和运行工况，其结构响应如图3所示。

图3 原始叶片结构响应

图4 原始叶片的挠度

总体来看，叶片应力分布均匀，仅在腹板和梁帽连接处出现了应力集中，最大Mises应力48 MPa。叶片所有单元的TsaiH失效因子都小于1，最大失效因子为0.649，所以基于该铺层铺设，叶片强度是满足要求。从结果可以看出，危险区域主要集中在梁帽中间部位。

通过经典层合板理论，可以计算出ABD刚度矩阵，进一步可以获得叶尖挠度。挠度如图3b所示，最大挠度为387 mm，远远小于叶片长度的15%（1125 mm）。

4.2 碳玻混杂复合材料叶片

叶片的材料由金属过渡到复合材料，最为突出的是碳纤维增强复合材料和玻璃纤维增强复合材料。前者比刚度和比强度性能优于后者，但成本和加工工艺仍是制约其广泛应用的重要原因。碳玻混杂是一种降低碳纤维应用成本的技术，通过控制混杂比可以达到成本和性能之间的平衡［21-23］。

图6 混杂叶片的挠度

针对复合材料潮流能水轮机叶片，在梁帽处以10%的层数混杂比引入碳玻混杂技术，对其进行失效分析。Mises应力云图和Tsai-Hill失效因子云图分别如图5a和5b所示。

图5 混杂叶片的结构响应

通过引入碳玻混杂技术，叶片最大Mises应力由63.9 MPa 下降到44.0 MPa ，TsaiH失效因子由0.65下降到0.59，极大地降低了叶片的最大应力和失效因子。同时叶片尖部最大挠度由387 mm降低到353 mm，进一步提高了叶片刚度。

玻璃纤维增强复合材料和碳纤维增强复合材料的密度分别为2.0 和1.58，混杂复合材料叶片的质量明显降低。

5 结论

本文基于有限元分析方法，对某型号潮流能水轮机复合材料叶片进行了结构分析。建立了基于Tsai-Hill失效准则的损伤模型，利用叶素动量理论计算了正常工况下的水动力载荷，分析了叶片的应力、挠度以及失效因子。此外，在梁帽处以低混杂比引入碳玻混杂技术并对混杂叶片进行损伤特性分析。结果表明：

（1）水轮机叶片的最大应力为48 MPa，失效因子0.650，叶尖挠度387 mm。

（2）碳玻混杂复合材料有利于改善复合材料水轮机叶片的失效，最大应力44 MPa，失效因子0.591，叶尖挠度354 mm。

（3）碳玻混杂技术为复合材料水轮机叶片的设计提供了重要的参考价值。