基于轨迹预测的冲突间隔管理

刘仁禹

（四川大学计算机学院，成都610065）

0 引言

随着国民经济和航空运输业的快速发展，空中航路使用率增加，传统的管制方法效率逐渐降低。基于航迹的管理（TBO）新一代智能空中交通管理的关键技术，航迹管理能够灵活设计飞行路线，结合轨迹推测对空中交通情况进行实时、准确的预测[1]，动态地掌握空中交通运行情况，实现空域管理，是未来智能空中交通管理的趋势。在降落过程中，进近管制区的特点是飞行密度大、潜在冲突多，成为飞行事故和事故特征的多发地带[2]，传统的线性系统不能满足日益增加的空中流量，逐渐向非线性系统拓展，非线性系统的控制发展迅速[3]，模糊系统通过简单的IF-THEN规则结合模糊隶属度函数能以任意精度逼近一个连续的非线性函数，利用模糊规则将模糊变量转化为精确数值，具有结构简单，数学描述方便的特点，因而成为描述非线性系统的主要方式[4]。

针对飞机在五边航线的降落过程和空域内的流量情况，对航迹进行预测并给出飞机在空间中的位置，是进行各种管制调度，特情处理的重要方法[5]，在航空管制安全距离要求的基础上，划分时间冲突间隔Tis，避免发生飞行冲突，并建立模糊控制器动态调整Tis，在时间管理上提升塔台的管制效率。

1 轨迹推测

轨迹预测与对于民航和军事空中管制等领域有重要价值，传统的航迹预测包括基于历史数据的数据挖掘方法，基于神经网络的模拟方法等[6]。实际中驾驶员是依据飞行计划中的航线在空域中航行，飞行航线由航路点组成，如图1所示，航线route由航路点P1、P2、P3、P4组成，飞机在当前位置沿航路点飞行，为精确预测飞机在航线上的位置变化，在传统航路点Pi的坐标基础上添加速度vi（i=1，2，3…）变量，根据轨迹计算模型，可以推算飞机在航线上精确的位置变化。

图1 飞行航线

如图2所示，在经纬度坐标系下，飞机的坐标包括纬度lat、经度lon、高度alt，将飞行运动分解为基于经纬度的球面坐标变化和基于海拔高度的垂直坐标变化。速度V分解为水平速度Vx和垂直速度Vy，飞行航向角为Hdg，速度Vx分解为方向互为垂直的Vnorth与Veast，且Vnorth方向与经线方向平行，Veast方向与纬线方向平行。

图2 运动分量

在水平速度方向上，飞行轨迹可以看作由一组直线和曲线连接而成，当飞行航迹为曲线时，航迹由许多小圆弧组成[7]。如图2所示，飞机沿航路点Pi、Pj飞行，航线PiPj的航向为hdg，计算公式为：

当飞机到达航路点Pi时，航向为Hdg，若Hdg=hdg，则飞机按原航向继续航行，飞行轨迹为直线；若飞机Hdg≠hdg，飞机调整航向，飞向航路点Pj，飞行轨迹为曲线。

在水平方向上飞机转弯时，调整坡度角为β（g为重力加速度，dt是时间积分区间），飞行变量变化公式为：

ax是水平方向加速度，ay是垂直方向加速度，航空管制要求飞机在不同高度采用不同的速度，不同型号的飞机加速度存在差异，则设定加速度ax的区间为[axmin，axmax]，垂直加速度ay的区间为[aymin，aymax]，在航路点Pi、Pj的速度为vi（Vxi，Vyi），vj（Vxj，Vyj），当速度的变化公式为（x为水平距离，y为垂直距离）：在经纬度坐标下计算飞机的位置变化与一般的直线不同，飞行距离要转化经纬度变化，计算公式为：

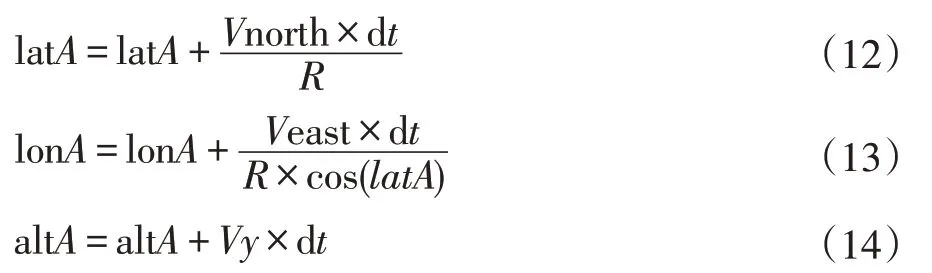
2 Tis模糊控制器

模糊系统是一种基于知识或者基于规则的系统，其决策是一个实值向量向一个实值标量所作的多输入单输出映射过程，并由IF-THEN规则为形式的知识所组成的规则库组成[8]。常见的模糊系统包括三种，纯模糊系统，TSK模糊系统，具有模糊器和解模糊器的模糊系统[9]，第三种模糊系统应用最为广泛。与经典集合中的隶属度函数不同，在经典集合中，用隶属度函数表示：

A={x∈U|x满足某些条件}

而模糊系统中的隶属度函数是区间[0，1]上的一个连续函数，U的取值范围是[0，1][10]，即：

如图3所示，模糊系统中的变量为语言值，例如“小”、“中”、“大”，语言变量对应的一定的实际值范围，词语由定义在论域上的模糊集合来描述，变量的x取值范围为区间[0，Xmax][11]。隶属度函数包括高斯隶属度函数、广义钟型隶属度函数、S形隶属度函数、梯形隶属度函数、三角隶属度函数等[12]。

图3 转弯航线

图4 隶属度函数

模糊系统包括四部分，模糊器将输入的确定值根据隶属度函数转化为相应的模糊量，模糊规则库由一组IF-THEN模糊条件语句组成，模糊推理机根据模糊规则和模糊运算输出模糊量，解模糊器将计算出的模糊值转化为准确数值。

图5 模糊系统

飞机在进离场过程中，沿五边航线飞行，如图6所示为五边航线俯视图，航线由航路点A-＞G组成。进场时，飞机降低速度，进入下风边DE，调整航向后进入底边EF，最后沿进场边EG进入跑道；离场时，飞机加速至起飞速度后沿离场边AB起飞上升，根据目标航向离场或者进入侧风边BC爬升离场。

图6 五边航线

飞机planei的速度为vi，航向为Hdgi。当满足降落要求准备降落时，飞机调整速度Vi和航向Hdgi加入起落航线。降落过程中，飞机planei从航路点D加入起落航线，沿航线DE，EF，FG降落机场，且在起落航线上按照航路点速度飞行，为避免发生碰撞，设相邻飞机加入起落航线的间隔为Tis秒，即飞机plane1加入航线的时刻为t1，飞机plane2加入航线的时刻应为t1+Tis。

空域内的飞机数量和飞行状态是影响管制的关键因素，和时间冲突间隔Tis存在非线性关系，根据空域内流量变化和模糊系统理论，建立Tis模糊控制器，动态调整间隔Tis。设空域内未加入航线的飞机数量为n，则未加入航线的飞机的速度均值VP=（V1+V2+···+Vn）/n，航向均值Hdgp=（Hdg1+Hdg2+···+Hdgn）/n。

Tis模糊控制器如图7所示，模糊控制器的输入变量为速度均值与航路点D的速度要求的差值即e=VPVD，论域为[-100，100]，另一输入变量为航向均值和航线DE的差值，即ec=HdgP-HdgDE（HdgDE为航线DE航向），论域为[0，360]。Tis的论域为[150，230]，模糊变量e、ec和模糊输出划分为7个模糊子，即e，ec，Tis={NB，NM，NS，Z，PS，PM，PB}，分别表示{负大、负中、负小、零、正小、正中、正大}。隶属度函数选择三角隶属度函数。基于专家经验建立模糊规则，推理方式采用两输入一输出的形式：“若A且B则C”，变量e，ec模糊控制规则表如表1。

图7 模糊控制器结构图

表1 模糊控制规则表

解模糊采用质心法，取隶属度函数曲线与横坐标围成面积的重心，作为模糊推理的最终输出值，即，质心法具有更平滑的输出推理控制，即使对应于输入信号的微小变化，输出也会发生变化。

3 仿真实验

在仿真软件中，绘制飞行航线route（D，E，F，G），飞机按航路点飞行，如图8，紫色线为ZUUU机场五边航线俯视图，飞机由航路点D加入航线，每架飞机按照固定速度模型V=f（t）在航线上飞行，沿航路点E、F、G降落至机场，航线上相邻飞机的时间间隔为Tis秒。

图8

使用Python语言搭建建立Tis模糊控制器，部分代码如下：

每隔1小时对空域中的飞行数据进行采样，获取未加入航线的飞机的速度和航向，计算模糊变量e=VPVD，模糊变量ec=HdgP-HdgDE，输入Tis模糊控制器得出Tis变化，如图9所示。

图9 Tis变化曲线

4 结语

基于模型的航迹预测结合五边降落航线，能够掌握飞机在航线上的准确位置，为塔台管制员提供辅助决策，基于模糊系统建立时间冲突间隔Tis模糊系统器，动态调整间隔Tis大小，避免飞机在航线内发生冲突，实验表明，模糊控制器能够根据空域情况动态调整间隔Tis，加强空中管制效率。