Kaup-Boussinesq方程的留数对称和相互作用解
呼 星 汝
西北大学 数学学院,西安 710127
非线性演化方程及其精确解在物理、自然科学等领域有着非常重要的作用,因此构造非线性发展方程的精确解一直以来都是广大数学物理研究的重要问题之一. 众所周知,对称群理论[1]和Painlevé分析理论[2-3]是发现和解决非线性演化方程的两大重要方法. 在可积系统中,获取非局域的方法主要有逆递推算子法[4]、Darboux变换法[5]、Bäcklund变换法[6-7]、截断的Painlevé方法[8]等. Painlevé分析是研究系统可积性的重要方法之一,其重要的一个推广是截断的Painlevé展开方法. 该方法不仅可以直接构造系统的Bäcklund变换和解析解,还可以用来构造系统的非局域对称,并且很多方程的相互作用解可以由非局域对称得到. 文献[9]在做非局域对称的Painlevé截断展开时发现,奇异流形的留数是一个非局域对称,称为留数对称[9]. 文献[10]通过Painlevé截断展开方法提出了相容的Riccati展开方法(CRE),此方法不仅可以用来证明方程的CRE可解性,而且可以根据可解性来构造方程的不同类型的相互作用解,例如孤立子、椭圆函数解等,这说明很多可积系统是相容Rccati展开可解并具有相互作用解的.
本文主要研究了如下形式的Kaup-Boussinesq方程[11]
(1)
方程(1)描述了浅水波运动,其中u(x,t)表示水平底部以上的水面高度,v(x,t)是相关的水平速度场. 当γ=2时,方程(1)可化为Boussinesq系统
(2)
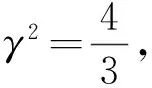
(3)
文献[11]利用F展开法得到了方程(1)的一些精确解;文献[12]给出了广义Kaup-Boussinesq方程的不变解和守恒律;文献[13]利用Euler-Lagrange变分原理得到了Kaup-Boussinesq方程的守恒律. 目前,方程(1)的留数对称及其相互作用解还未被研究.
本文首先利用截断的Painlevé展开方法构造了Kaup-Boussinesq方程(1)的留数对称,并通过引入新的函数关系使之局域化;然后通过CRE方法证明了方程(1)的相容Riccati展开可解性,并利用此性质构造了方程(1)的相互作用解. 在求解的过程中,根据Riccati方程的解和椭圆方程的解,再结合Jacobi椭圆函数和第三类不完全椭圆积分构造出了一组新的椭圆周期波与孤立波相互作用解. 通过对KB方程的研究发现,CRE方法与Jacobi椭圆函数、第三类不完全椭圆积分的结合是探索非线性方程新的精确解的一种十分便捷且有效的方法.
1 留数对称及其局域化
对于Kaup-Boussinesq方程,相应的Painlevé截断展开式为
(4)
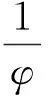
(5)
并且φ满足如下的Schwarzian形式
(6)
其中
Schwarzian形式(6)在下面的Möbious变换
(7)
保持不变. 把(4)式代入方程(1)可以得到下面的定理:
定理1(自Bäcklund变换定理) 如果φ满足方程(6),则
(8)
是方程(1)的一个解.
定理2Kaup-Boussinesq方程具有下面形式的留数对称:
(9)
其中:u,v,φ满足(8)式;σu,σv分别为u,v的对称.
证方程(1)的对称方程是
(10)
把(9)式代入(10)式中,在方程(6)和(8)的帮助下,(10)式是成立的.
为了使留数对称非局域化,我们引入两个新的变量
φx=fφxx=g
(11)
将Kaup-Boussinesq方程的非局域留数对称局域化为扩展系统
(12)
的Lie点对称
(13)
相应的Lie点对称向量场为
(14)
最后根据Lie点对称第一定理,解下列初值问题
(15)
得到如下的对称群变换定理:
定理3若u,v,φ,f,g是扩展系统(12)的解,则
(16)
也是该系统的解,其中ε是任意群参数.
2 CRE可解及其相互作用解
2.1 CRE可解
通过领头项分析,我们可以得到KB方程有如下形式的解:
(17)
式中v0,v1,u0,u1,u2是关于x和t的待定函数,R(w)是Riccati方程
Rw=a0+a1R(w)+a2R(w)2
(18)
的解,这里a0,a1,a2是任意常数. 将 (17)式和Riccati方程(18)式代入到方程组(1)中,消去R(w)的各阶系数,可以得到
(19)
其中w满足Schwarzian形式:
(20)
显然,如果w是相容性方程(20)的解,则由R(w)和(19)式可知(17)式是方程组(1)的解.
综上,我们得到如下定理:
定理4对于给定的方程(20),如果w是方程(20)的解,则
(21)
是KB方程组(1)的解,其中v0和u0满足方程(19),R≡R(w)是Riccati方程的解.
2.2 KB系统的相互作用解
我们知道Riccati方程有如下形式的双曲正切函数解:
(22)
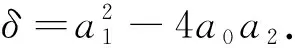
(23)
由定理4可知,只要找到相容性条件(20)的解,代入到方程(23)就可以得到KB方程的解. 我们假设w具有如下特殊形式的解
w=k1x+p1t+W(k2x+p2t),W(k2x+p2t)=W(ξ)=W
(24)
其中W1≡W1(ξ)=Wξ满足椭圆方程:
(25)
式中Ci(i=0,…,4)是常数. 把(24)式和椭圆方程(25)式代入到相容性方程(20)中,经过计算得到:
(26)
显然椭圆方程(25)的通解可以用雅可比椭圆函数来表示,将(25)式的解取为如下形式:
W(ξ)=cEπ(sn(ξ,m),n,m)
(27)
其中,sn(ξ,m)为一般的椭圆正弦函数,Eπ(sn(ξ,m),n,m)是第三类不完全椭圆积分,则
w=k1x+w1t+W(ξ)=k1x+w1t+cEπ(sn(k1x+w1t,m),n,m)
(28)
把(28)式代入到(23)式中,即可得到方程组(1)的一组孤立波与椭圆周期波的相互作用解:
(29)
式中
S=sn(ξ,m)
C=cn(ξ,m)
D=dn(ξ,m)
取参数如下:
(30)
则KB方程的孤立波与椭圆周期波的相互作用如图1所示.
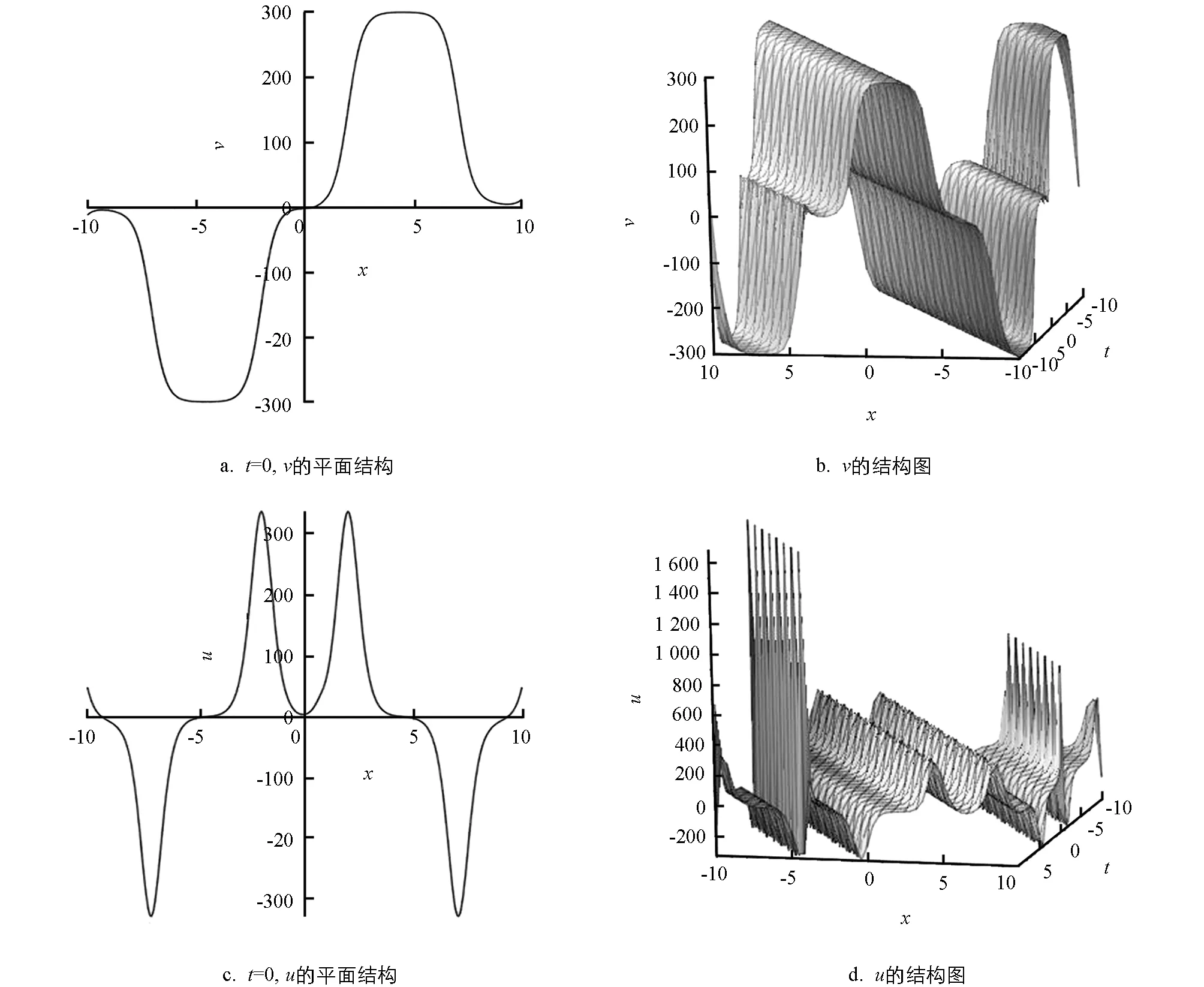
图1 KB方程的孤立波与椭圆周期波的相互作用示意图
3 结束语
本文以具有物理背景的Kaup-Boussinesq方程为研究对象,运用数学软件Maple,通过Painlevé截断展开法得到了方程的留数对称,并且将留数对称局域化为扩展系统的Lie点对称. 留数对称的局域化过程,是求解非线性演化系统相互作用解的重要方法之一. 此外,在Riccati方程的帮助下,证明了KB方程是CRE可解的,并且给出了方程组(1)的孤立波与椭圆周期波相互作用解. 最后通过计算机模拟给出了孤立波与椭圆周期波相互作用解的图像. 由此可知,CRE方法不仅可以构造可能存在的可积系统,而且对于构造不同类型的相互作用解是非常有效的.

