一类随机偏微分方程的有效近似
李益军,陈光淦
四川师范大学 数学科学学院,成都 610068
随机偏微分方程应用于物理学的众多领域,近年来在各数学分支的发展推动下,随机偏微分方程也得到相应发展和研究,如关于随机Burgers方程[1]、随机Swift-Hohenberg方程[2]等的研究.
在内积为〈·,·〉,范数为‖·‖的Hilbert空间H中研究如下的非线性随机偏微分方程
(1)
其中u=u(t,x,ω),x∈有界区域D. 小扰动项εLu表示与分支的距离. 算子A假定为自伴随且非正的,噪声由一般的Q-维纳过程给出,详见第一节.
本文在稳态改变的附近,运用时间尺度变换来导出方程的有效近似系统. 值得指出的是,扰动强度与噪声强度对系统的有效近似有着重要影响,使得有效近似系统的近似形式和收敛率有着重要差异[3-7].
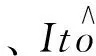
1 预备知识
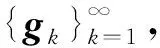
用N:=kerA表示A的核空间,T:=N⊥表示N在H中的正交补空间.Pc为从H到N的投影,Ps为从H到T的投影. 假设Pc,Ps与A可交换,A-1dW存在,假设N为n维,其标准正交基为{g1,g2,…,gn}.
分数阶Sobolev空间Hα定义如下
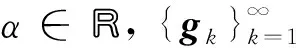
定义算子Dα:Dαgk=kαgk,因此有‖u‖α=‖Dαu‖.
线性算子A生成解半群eAt满足
引理1在假设1下,存在常数M>0,K>0,使得对所有的t>0,β≤α,u∈Hβ有

假设3B是一个从Hα×Hα到Hα-β的有界双线性算子,其中α,β由假设2给出. 不失一般性,可假设B是对称的,即B(u,v)=B(v,u),且满足PcB(u,u)=0,u∈N. 本文中,取B(u,v)=uv.

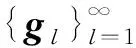
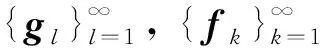
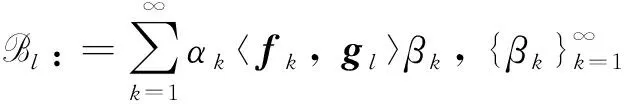
定义1定义随机卷积
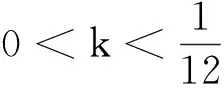
τ*:=T0∧inf{T>0|‖a(T)‖α>ε-k或‖ψ(T)‖α>ε-2k}
定义3对于一个实值的随机过程族{Xε(t)}t≥0. 如果对每个p≥1都存在一个常数Cp满足
则我们称Xε=O(fε).
最后指出,用字母C表示所有正常数,它依赖于T0,k,α,B,Q,L,A及其给出的数据. 同时规定如下简记符号:Bs:=PsB,Bc:=PcB. Lc,Ls,Ac,As,Wc,Ws同理.
2 主要结论
对于方程(1),将其解u(t)分解为两部分
(2)
其中a∈N,ψ∈T. 选取时间尺度变换为T=εt,将(2)式代入(1)式,并分别做Pc,Ps投射可得到
(3)
和
(4)
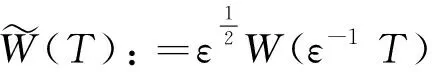
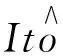
(5)
其中r(T)是ε的高阶项. 忽略(5)式中的小项,可以得到
因此
令b(T)满足方程
(6)
则方程(6)就是逼近随机偏微分方程(1)的有效近似系统(也被称为振幅方程[10]).
进一步,由(3)和(5)式可得
(7)
其中
(8)
下面给出本文主要结论.
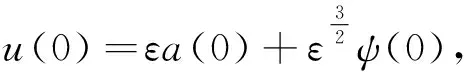
(9)
3 主要结论的证明
为证明本文主要定理1,需要依次估计方程(2)中的ψ(T),方程(8)中的R(T)以及方程(6)中的b(T).
3.1 ψ有界性的证明
引理2在假设1,2,3,4下,T>0,z(T)是如下方程的解
(10)
则对ε∈(0,1),T≤τ*有
(11)
证方程(4)的温和形式为
因此
下面依次估计I1,I2,I3.
由引理1,0≤β 令 η=ε-1K(T-τ) 则 (12) 类似的,对所有的T≤τ* (13) 进一步 (14) 结合(12)-(14)式,(11)式得证. 引理3[8]在假设1,4下,取方程(10)的初值z(0)满足‖z(0)‖α=O(1). 则对每一个k0>0,p>1和T>0,存在常数C>0使得 (15) 证这是一个标准的OU-过程有界估计,其证明过程可参考文献[8]中引理20的证明,区别仅在于ε的指数不同. 引理4在假设1,2下,利用定义2中τ*的定义,对所有的ε∈(0,1), (16) 证利用引理1和假设2,与引理2中I1的证明类似,可得对T<τ* 引理5在假设1和假设3下,利用定义2中τ*的定义,对所有的ε∈(0,1), (17) 证利用引理1和假设2,与引理2 中I2的证明类似,可得对T<τ* 引理6在引理2、引理3、引理4、引理5成立的条件下,对p>1和所有的k0>0,存在常数C>0,使得 (18) 证根据(11)式,由三角不等式和引理2,有 再根据引理3、引理4、引理5,对于k0≤2k,引理6得证. 引理7在假设1,2,3,4下,对所有的p>1,存在一个常数C使得 (19) 与引理2中I1,I2,I3估计类似,对(8) 式中定义的R(T)各项有 (20) (21) (22) (23) (24) (25) (26) 引理8在假设1,2,3,4下,设随机过程b(T)满足E‖b(0)‖≤C与方程 (27) 则对于T0>0,存在一个常数C使得 (28) 其中使用了〈dt,dt〉=〈dt,dW(t)〉=〈dW(t),dt〉=0,〈dW(t),dW(t)〉=dt. 在(28)式两边同时取期望有 由Gronwall不等式得 E|b(T)|2p≤C 即 对(28)式先取上确界,再取期望有 再使用B-D-G不等式和Hölder不等式得 (29) 证令 h(T)=a(T)-b(T) 则 (30) 对(30)式等式两边在[0,T]上积分后取上确界,再取期望得 (31) 故 引理10设集合Ω*⊂Ω且在Ω*上成立 则有P(Ω*)≥1-Cεp. 证由Ω*定义有 利用Chebychev不等式及引理6、引理7、引理8,对充分大的q(q为p的共轭指数)有 P(Ω*)≥1-Cεqk≥1-Cεp 定理1的证明 结合定义2与引理10可知 结合三角不等式与(2)式、(29)式,在Ω*上有 即 在Ω*上成立,定理1得证.3.2 R(T)有界性的证明
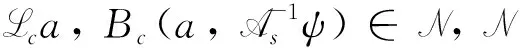

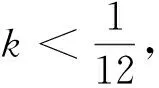
3.3 b(T)的先验估计


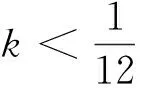
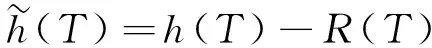
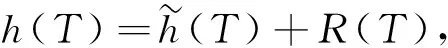
3.4 定理1的证明

