基于拉格朗日松弛算法的应急物流配送车辆调度模型优化研究
张文晖
(广东省珠海市交通运输局, 广东 珠海 519003)
各种紧急情况和事故会严重影响公共安全及人员和财产安全。重大灾难性事故发生后,往往需要启动紧急救援,包括医疗物资、防护装备、安置及生活保障物资运输等。应急物流下的车辆调度问题(Vehicle Rooting Problem,VRP)是积极应对各种紧急突发事件的关键因素。VRP基于具有已知装载点(供应点)、卸载点(事故点)和已知可用路线的运输网络,在满足其他外部约束条件(如对不同物资的需求、车辆类型和容量、时间窗要求等)的情况下,选择最合适的行驶路线以达到预期目标要求(如路程或时间最短、保证时间前提下费用最少等)。 有关VRP的文献资料很多,由于其复杂性,多数着重于以最小化运输费用或最小化运输时间作为目标函数来构建模型。如文献[1-5]根据不同条件下的要求,构建了以运输费用最小化为优化目标的VRP模型;文献[6]提出同时考虑送货和提货的车辆路径问题,并采用并行变邻域搜索算法进行求解;文献[7]提出带有软时间窗的VRP模型,并采用禁忌搜索算法进行求解;文献[8-9]根据模糊理论,采用两阶段变邻域禁忌搜索算法解决模糊需求下车辆路径选择问题;文献[11-13]针对各种应急条件下物流车辆路径问题开展模型构建,并分别采用免疫算法、PSO 算法等进行求解。为提高对大型突发事件应急物流的响应能力,该文在相关研究的基础上,综合考虑应急物流需求的急迫性、多部门及市场主体参与性、弱经济性等内在特点,将VRP问题转化为多模式的分层网络问题,构建多目标数学优化调度模型并采取拉格朗日松弛算法进行求解。
1 问题描述及模型建立
1.1 多模式分层网络设计
针对各类突发事件进行应急货物运输车辆调度时,由于事件发生点的随机性,通常会出现多个可能的需求点与供应点,且需转换2种以上运输方式。为满足应急物流需求,依据需求特点,展开不同运输方式的多模式网络分层设计。该模式网络通常有四类顶点和三类弧(见图1)。四类顶点分别为中转点、映像点、供应点、需求点,其中:中转点表示该节点仅为各种运输方式转换的场所,且不承担货物存储任务;映像点表示该节点为各运输方式下实际发货(供应)或接收货物(需求)的点;供应点表示该节点为应急货物的提供场所,它通过各模式网络层上的供应映像点发运货物;需求点表示该节点为应急货物的需求场所,它通过各模式网络层上的需求映像点接收货物。三类弧分别为载重弧、转换弧、映像弧,其中:载重弧表示货运通路,连接所有映像点和中转点,与载重弧相关的成本为运输成本;转换弧表示将不同模式网络层中的运输方式进行连接的通道,转换过程将产生相关转运成本;映像弧仅表示映像点与需求或供应点之间的联系,其相互间发生的供需运量关系、相关费用和时间消耗等均忽略不计。

图1 多模式分层网络结构示意图
图1中,a、b为需求点,c、d为供货点,e、f为中转点。该多模式分层网络由3种运输方式组成,故对应3种模式层。如c供货点可通过模式层一、二中c′、c″的不同运输方式映像点向各需求点运送货物;f中转点可在转换弧上通过f″和f‴2个不同运输方式中转点为模式层二、三的车辆进行转换等。车辆可在不同模式层上被调度循环使用,从而形成循环车辆流。
在应急物流的车辆调度中,通常需设置某些特殊的约束条件:1) 车辆可在网络上任意一个点被调用;2) 没有固定停车场,因为车辆完成运输任务后通常不必返回原始位置,而是停在原地;3) 车辆流只能流过载重弧;4) 不同模式层上最大车辆流不能超出载重弧的最大容量限定,同时货物流量不能超出货运车辆的最大额定量。
尽量缩短货物在途运输时间是应急物流车辆调度的主要目标,故时间参数是调度中需考虑的首要因素。引入时间参数后,要解决的问题就转化为四维空间优化问题。为方便起见,将货运调度方案总体所需时间周期划分成若干等长的单位时间段,在车辆调度优化模型中设置的时间参数均以时段数来表示时间维度值。这样可使各供需节点的供货量或需求量与应急救援所规定的不同时间要求更加匹配,因为以一个预定的时间周期来进行调度计划安排,可能会导致车辆在完成任务后出现不必要的闲置时间,而采用时间段可更灵活地根据需求进行调度安排。需注意的是,时段长度的取值不能过大,也不能过小,过大可能导致车辆在完成任务后出现不必要的闲置时间,过小则会导致车辆路径长度呈指数增长。引入时间维度后,多模式分层网络便转换成了时空网络(见图2),该时空网络由图1中第二模式层抽象而来,其中每两点间的车辆行驶路线用虚线连接。车辆的起始点在c与d点,车辆可根据需要在时空网络的单向可行路线中按照调度指令选择完成配送任务的路线。

图2 模式层二的时空网络结构示意图
应急物流VRP是一个多目标(减少运输时间、降低运输费用)规划问题,其中运输费用的产生主要体现在载重弧上车辆行驶费用和车辆在各中转点进行运输方式换载时发生的费用。在构建运输时间最小化目标函数模型时,可设置车辆未按时到达的罚函数参数,通过车辆延期到达的罚函数系数来反映不同需求点对应急物资的时间需求程度。该罚函数系数可由未满足时间要求而顺延一个时间段对目标函数所造成的单位增量来定义。
该方法的优点在于适用性较灵活,如需要以最小时间为目标函数,可将货运费用参数值设置为零;而当救援行动持续一段时间,应急情况相对缓解后,需考虑救援货物运输费用最小化时,可将模型中时间参数延期的罚函数系数赋值为零。
1.2 模型构建
1.2.1 假设条件
(1) 在应急救灾过程中运行的货运车辆均为额定满载。
(2) 载重弧上运行的货运车辆均以单位时段数来计量运输时间,运行时间小于1单位时段的按1单位计量。
(3) 车辆在转换弧上耗费的时间均按1单位时间段数计量。
(4) 车辆运行过程中所有相关费用函数都成线性关系。
(5) 各供应点和需求点上的货物可供量与需求量已知。
(6) 不同模式层下同一种运输方式的车辆规格相同。
1.2.2 目标函数与约束条件
目标函数为:
min(C1+C2+C3)
(1)
(2)
(3)
约束条件如下:
(i∈S,g∈G,t∈T)
(4)
(i∈R,g∈G,t∈T)
(5)
(i∈FE,t∈T,g∈G,m∈M,i′∈R∪S)
(6)
(7)
(8)
(i,j)∈CA)
(9)
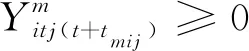
(10)
(t∈T,m∈M,(i,j)∈CA)
(11)
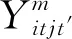
模型中的开始时刻为货运的最早发运时间,由车辆行驶成本、运输方式转换成本、车辆未按时到达所带来的目标函数增加值构成目标函数。
约束条件由货物流约束、车辆流约束、关联约束构成,其中:货物流约束对供应点向需求点运输的货物进行约束;车辆流约束是对车辆在各供应点和需求点之间流转的约束;关联约束将货物流与车辆流集成为一个整体相互关联约束。式(4)~(7)为货物流约束,式(4)表示供应点库存量与供应点向各需求点运输货物的量平衡关系,即i点通过其映像点运送的g货物数量=i点在上一时间段已延期到本时间段尚未发货的货物量+需新增的供货量-延期到下一时间段运送的货物量;式(5)表示需求点接收的货物量未满足需求,仍需增加供货量;式(4)、(5)反映供应点与需求点之间货物量的供需平衡关系;式(6)等式两边分别为货物流入量和流出量,反映中转点或映像点进出货物量间的平衡关系;式(7)是非负条件约束。式(8)为车辆流平衡约束式,为进入中转点或映像点的车辆总数等于已完成货运任务并离开该点的车辆数与仍需停留在该点待命的车辆数之和。式(9)表示在弧(i,j)上运行的车辆数不能超过弧(i,j)所限制的最大容量,为车辆流的上限约束。式(10)表示车辆流决策变量值非负且为整数。式(11)反映车辆流与货物流之间的关系,为两者间的关联约束,即通过载重弧(i,j)上货运车辆的货物运载量不能大于车辆的额载量。
2 拉格朗日松弛算法在VRP中的应用
2.1 问题解的框架
根据上述对应急物流车辆调度VRP模型的分析,车辆运营成本、运输方式转换中产生的费用及货运车辆延期需求惩罚费用共同构成该模型的目标函数,模型的约束条件由车辆流、货物流及其两者之间相互关联约束构成。对于后者,如果能采用相应的方法松弛该关联约束,使模型转化为车辆调度与货物运输2个子问题,求解模型的难度将大大降低。根据该思路,采用拉格朗日松弛算法进行求解。
引入该算法后的目标函数为:
min(C1+C2+C3+C4+C5)
(12)
(13)
式中:Wmijt为拉氏乘子向量组,简称Lag(OP)。
两者相互关联约束松弛之后,可将拉式乘子问题的求解过程分为对货物流Lag1(X)与车辆流Lag2(Y)的计算。Lag1(X)的目标函数由式(2)、式(3)、式(12)组成,其约束为式(4)~(7)。为避免关联松弛造成车辆在载重弧上的货物流超限,在Lag1(X)中加入车辆货物流量上限约束式:
(t∈T,m∈M,i∈FE,j∈FE)
(14)
车辆流Lag2(Y)的目标函数由式(1)、式(13)组成,其约束集为式(8)~(10)。
求解Lag(OP)最优解的步骤:

(2) 利用子梯度法计算Lag(OP)。将Lag(OP)转换为2个子问题Lag1(X)、Lag1(Y)分别进行计算,求得最优解Xk和Yk。再求出目标函数值Sk,判断Sk和LB两者的大小关系,若Sk>LB,则利用LB=Sk判断2个最优解是否满足约束条件。若满足,且目标函数值Sk小于OP*,则令OP*=Sk,执行步骤3;否则转入步骤4。
(3) 退出循环的条件。1) 最优解Xk和Yk是否满足关联约束等式成立的条件;2) (OP*-LB)/OP*<α(α为收敛率);3)k=TK(TK为限制循环的次数)。若满足条件1,则可得出最优解为Sk并输出。若条件2中OP*距离下限解LB的比率小于收敛率α,则OP*是可行解并输出。满足条件3时,循环便直接退出,输出Lag(OP)的最优解。若循环不满足上述3个条件,则执行步骤4。
(4) 按式(15)求解拉氏乘子步长θk。将Xk和Yk代入式(15),得到步长θk。如果在循环时LB的值不增加,但目标函数值必须收敛,则将比例因子λ减少至原来的一半,即λ=λ/2,执行步骤5。
θk=λ·(OP-LB)/
(15)
式中:λ为比例因子,其初始值为2。
(16)
2.2 子问题解法分析
Lag1(X):货物流子问题。根据上述对多模式分层网络的分析,实际上Lag1(X)问题可看作多种货物应急调运的最小费用流问题,可应用列生成算法得出最小费用流。弧的费用可采用货物流目标函数中式(2)、式(12)直接表示和计算,而式(3)需先转换为弧形式,再进行计算。如果应急救援货运只考虑时间最短而不在乎费用多少,则可将式(2)去除,直接求解运输时间最短路径。

3 算例分析
在某灾害发生地区,设应急供应点、需求点与中转点总量为8~12个,任选供应点与需求点,并不受坐标的影响。设每相邻点之间弧的货运周期为1~10,货运计划的周期数为以网络中最长弧的货运周期数为基数与3种类型点数的乘积之和。采用2种不同运输方式对该应急货运调度算例进行分析。设在单位时段内,2种运输方式单位车辆的运输费用分别为10和100单位。 计划执行之初,车辆可在任意点停留。每种货物每单位需求延时惩罚80单位,在调度计划中最多运输3种货物。为保持应急货物供需平衡,设每类货物的运输量≤500单位,每类货物的供应点不超过3个,且每个需求点的货物需求量为0~100。设Lag(OP)最优求解步骤3中的收敛率α=0,应用拉格朗日松弛算法、单纯形法与分支定界法结合算法对算例进行求解,将2种算法得出的最优结果进行检验和比较。共进行10个算例任务测试,结果见表1。
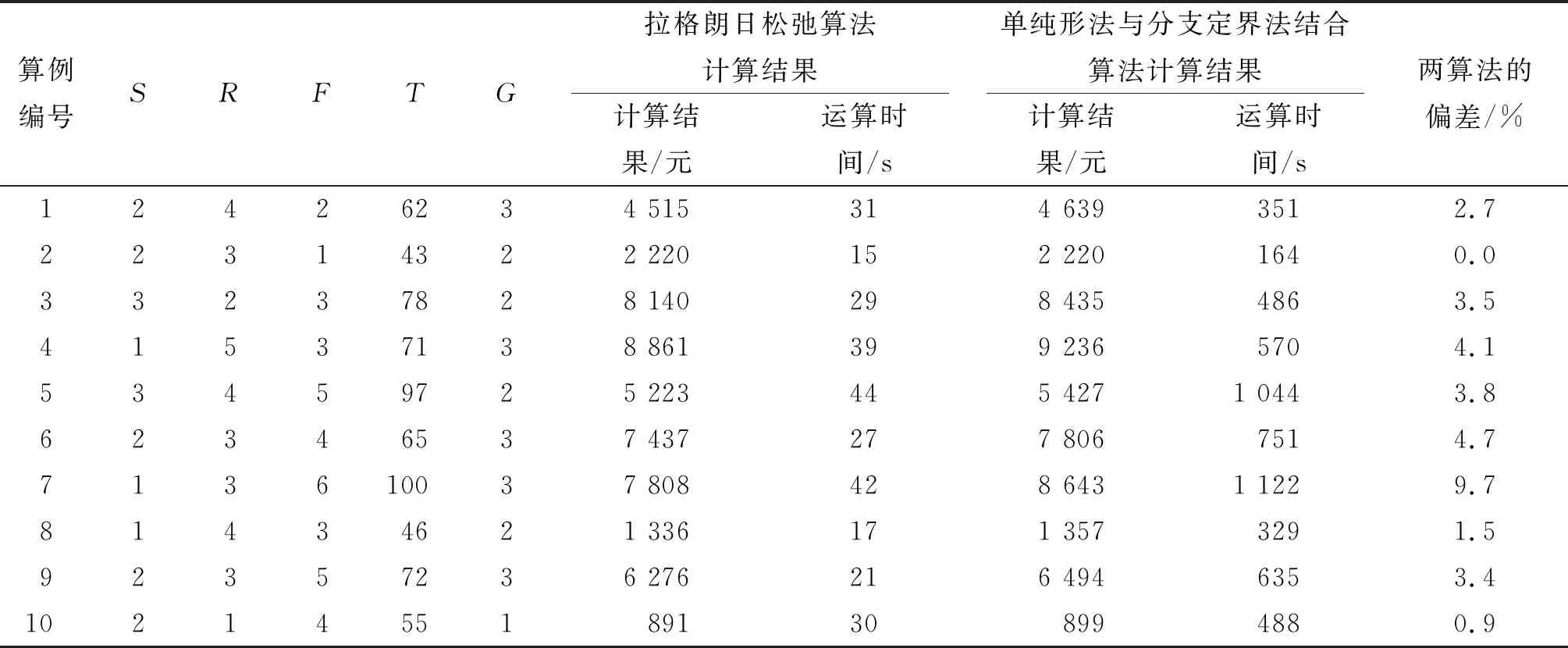
表1 算例测试结果检验和比较
由表1可知:除算例7外,其余测试算例2种算法求解结果的偏差都小于5%,且各测试结果的平均偏差小于3.5%;偏差值与货运计划的时段数成正相关关系。算例2和10,由于运输计划时段数相对较少,2种算法计算结果之间的偏差均小于1%。
4 结语
该文基于应急物流的特点构建应急物流车辆调度VRP问题的多目标组合数学模型,在运用拉格朗日松弛算法的基础上,将拉式乘子问题简化为车辆流和货物流2个子问题,采用网络流算法分别求解。算例测试结果表明,该方法具有较好的收敛性与有效性,可为应急救灾指挥中心制订车辆调度方案提供依据。

