犁底层容重对微咸水膜下滴灌土壤水盐运移分布的影响

胡文同，栗现文，江思珉

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.西北农林科技大学水利与建筑工程学院，陕西杨凌712100；3.同济大学土木工程学院，上海200092）

0 引言

我国是一个农业大国，又是一个水资源短缺且时空分布极不平衡的国家，淡水资源短缺已成为影响农业可持续发展的主要问题。同时，我国微咸水资源储量多、分布广、开采条件较好[1,2]，高效利用微咸水资源已成为缓解淡水供需矛盾的重要途径。膜下滴灌技术被认为是目前最合理有效的微咸水开发利用技术[3,4]，但使用不当会造成土壤积盐，不利于农业的可持续发展[5-7]。有学者认为微咸水膜下滴灌农田是否积盐的临界灌溉水矿化度为3.0 g/L[8]。

目前，对层状土壤水盐运移规律的研究，主要集中在黏土夹层和夹沙层[9,10]，而对犁底层的研究相对不足。犁底层表现为土壤密实程度变化[11]，改变土壤水力性质，影响土壤水分及溶质运移和分布。研究发现犁底层改变层状土壤水分入渗过程、湿润锋、累积入渗量[12]。张建兵等[13]发现犁底层能够阻碍盐分运移而汇聚于该层，而樊慧敏等[14]通过对渭北农田取样发现，土壤容重对含盐量有明显的异位效应。但在膜下滴灌条件下，不同容重犁底层对土壤水盐运移分布的影响尚不明确。

随着计算机技术的快速发展，数学模拟模型HYDRUS 已广泛应用于滴灌及层状土壤水盐运移分布模拟研究，为探究土壤水盐变化提供了技术支持[12,15,16]。如Roberts 等[17]采用HYDRUS-2D/3D 模拟地下滴灌土壤水盐运动，分析不同滴灌管埋深和灌溉水矿化度的地表积盐问题；Xu 等[18]通过田间灌溉试验与HYDRUS-2D数值模拟发现灌溉对土壤脱盐有明显影响，模拟值与实测值的偏差小于0.5%；杨霞等[12]通过东北寒区分层土壤、均质土壤室内入渗试验与HYDRUS-2D数值模拟得出，犁底层抑制土壤水分下渗，模拟值与实测值吻合；李远[19]利用HYDRUS 进行三维入渗试验发现，土壤容重越大，垂直湿润锋越小，水平湿润锋越大、脱盐系数越小。但很少有学者利用HYDRUS-2D系统研究犁底层容重对微咸水膜下滴灌土壤水盐运移分布的影响。

本研究利用HYDRUS-2D软件建立相同土质不同犁底层容重的二维层状土壤水盐运移模型，分析犁底层容重对微咸水膜下滴灌土壤水盐运移分布的影响，并通过模拟结果的溶质示踪量化不同模拟情景的排水来源，可为田间合理利用微咸水及灌溉排水提供参考。

1 模型与方法

1.1 概念模型

在HYDRUS-2D 的Geometry 模块构建水平方向为150 cm(田间一膜宽度，灌水模式为“一膜双管”)，垂直深度为100 cm 的土壤水流、溶质二维运移模拟域，如图1所示。上边界不考虑蒸发和降水，滴头处设为变流量边界；下边界不考虑地下水的影响，设为自由排水边界；左右边界为零流量边界。溶质运移模型边界条件均为第3类边界条件，在滴头处，滴灌时溶质通量为灌溉水溶液浓度，无滴灌时为零；零流量边界处溶质通量也为零。

图1 土壤水流、溶质运移概念模型Fig.1 Conceptual model of soil water and solute transport

1.2 水分运动方程

模型采用修改后的Richards方程描述土壤水分运动[20]：

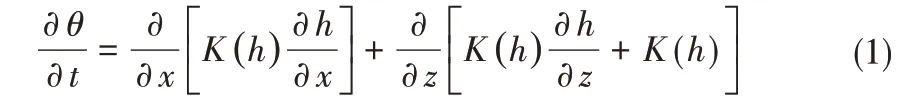
式中：θ为土壤体积含水率；h为土壤压力水头，cm；t为入渗的时间，h；x为横向坐标，cm；z为垂向坐标，cm；K(h)为非饱和导水率，cm/h。

土壤水分运动初始条件为：

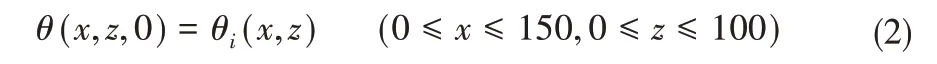
式中：θ(x，z，0)、θi(x，z)为0 时刻i节点土壤体积含水率，假设各模拟情景初始土壤体积含水率为0.15。

土壤水分运动边界条件：

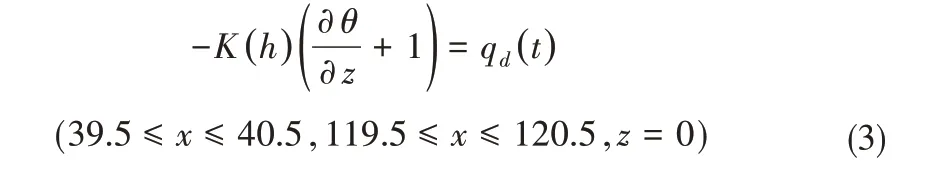
式中：qd为滴头流量，cm/h，有灌水时为100 cm/h，无灌水时为0。

土壤水力特性根据van Genuchten-Mualem 模型[21]表示为：

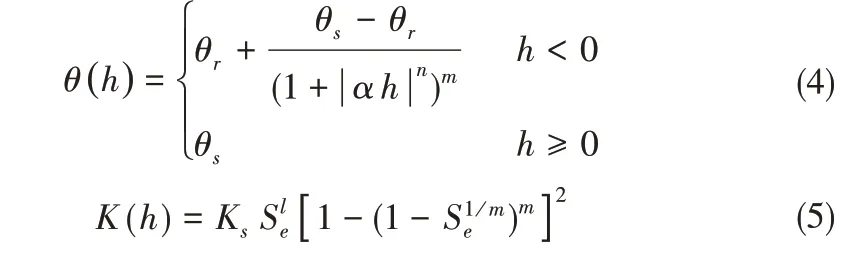
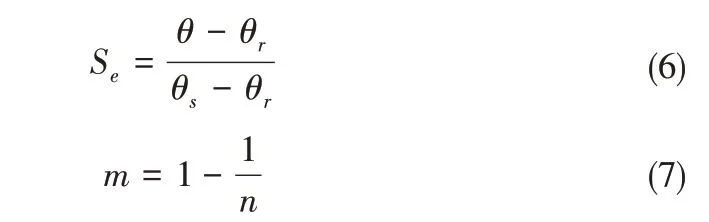
式中：θs为土壤饱和体积含水率；θr为土壤剩余体积含水率；Ks为土壤饱和水力传导度，cm/h；Se为土壤有效饱和度，%；α、n、m、l均为拟合参数，l通常取0.5。

1.3 溶质运移方程

在溶质运移模拟中考虑对流和弥散2种运动的影响。溶质运移方程如下[20]：

式中：c为土壤溶液中溶质浓度，g/L；D为弥散系数，cm2/h；q为体积通量，cm/h。

土壤溶质运移初始条件为：

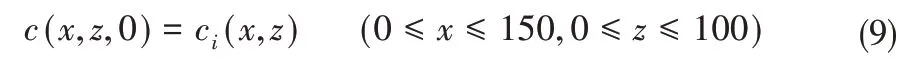
式中：c(x,z,0)、ci(x,z)为0 时刻i节点土壤水矿化度，g/L，假设各模拟情景土壤水初始矿化度为1.0 g/L。

土壤溶质运移边界条件：

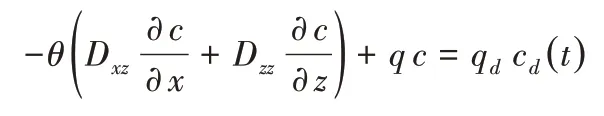
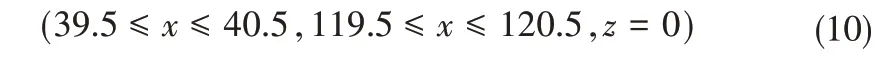
式中：cd为滴灌用水矿化度，g/L，为3.0 g/L。

1.4 参数设定

1.4.1 土壤性质

模型土壤质地选自文献[19]，其中沙粒(0.05～2 mm)、粉粒(0.05～0.002 mm)和黏粒(＜0.002 mm)含量分别为51.4%、26.6%和22%。

1.4.2 土壤水力参数

本研究利用HYDRUS-2D 模型中的Rosseta 模块，根据土壤质地(沙粒、粉粒、黏粒含量)和土壤容重，预测不同容重土层土壤水力参数。

1.4.3 溶质运移参数

研究表明，溶质运移弥散度与土壤容重呈线性相关[22]。因各层位土壤为各向同性，故认为纵、横向弥散度相同。弥散度(α，cm)与土壤容重(ρ，g/cm3)的关系参照文献[19]：

1.5 情景设定

为系统探讨犁底层容重对土壤水盐运移分布影响，设置4种情景(见表1)，其中S1 为均质情景，S2～S4 情景20～40 cm 处犁底层容重不断增大。由HYDRUS-2D 的Rosseta 模块和式(11)，确定不同容重土层的土壤水力和弥散度参数(见表2)。

表1 不同犁底层容重模拟情景土壤性质Tab.1 Soil properties of different plow pan bulk density simulation scenarios

表2 模型水力及溶质运移参数Tab.2 Hydraulic and solute transport parameters of the model

模拟时间设定为63 h，其中，灌水时间15 h，重分布时间48 h。在进行迭代计算时，离散时间单位为h，初始时间步长0.000 1，最短时间步长0.000 1，最大时间步长为120，θ迭代精度为0.01，最大迭代次数取10。设置网格尺寸为2 cm，在滴头和和土壤容重突变处加密单元格。在左侧滴头及两滴头中间10、30、50、70、90 cm 深度处设置观测点(见图1)，用于观测各土层土壤水盐动态变化。因膜下滴灌土壤盐分主要集中在0～60 cm 土层[23，24]，在模型10、30、50 cm 深度每隔10 cm 设置一个观测点，每个深度设置16 个观测点，分别用于对耕作层（0～20 cm）、犁底层（20～40 cm）和底土层（40～60 cm）水盐状况进行统计分析。

1.6 敏感度指数

土壤水力参数对土壤水盐运移会产生重要影响。前人研究表明，土壤水盐运移对θs、n、Ks、αL的敏感性较强，因此，选择上述参数进行局部敏感性分析。采用扰动分析法，将各参数在基准参数的基础上分别上下扰动5%和10%。定义敏感度指数L为：

式中：n为扰动次数；Δi为扰动值，分别取-10%、-5%、+5%、+10%；m为观测点数（分别为N1、N2、N3、N6、N7、N8），m=6；p为观测时间点，分别为灌水结束、灌后24 h 及48 h；θ0为基准参数情景对应的土壤含水量。

1.7 数据统计与情景

利用Excel 对HYDRUS-2D 输出文件的土壤水盐数据进行汇总和计算；采用SPSS 进行统计特征值分析、单因素方差分析和配对样本T检验。

2 结果与讨论

2.1 犁底层容重对土壤水盐运移规律的影响

2.1.1 犁底层容重对土壤水分运移规律的影响

模拟结果显示饱和体积含水量(θs)随土壤容重(ρ)增加而降低(θs=-0.252 6ρ+0.773 9，R²=0.999 5)。图2 为模拟过程各情景滴头及2 滴头中间不同深度θ变化过程。对比发现，处于相同层位的观测点有相似的变化规律：饱和含水率相同且模拟结束后θ变化规律基本一致。各情景N6～N8 处θ开始变化所需时间明显长于相同层位观测点N1～N3，但N9、N10处θ开始变化所需时间与相同层位观测点N4和N5基本一致，说明滴灌条件下，土层水分经过犁底层后逐渐呈层状运动。灌水结束后，犁底层容重越大，耕作层N1 和N6 处θ越大，犁底层N2和N7 处Se越高，说明犁底层对该层及其上层土壤涵养水分具有积极作用，且容重越大效果越明显。其原因为犁底层容重越大，土壤稳定入渗率越小[25]，等量水分下渗需要的时间越长。底土层N3 处θ开始变化所需时间：S1(6.5 h)＜S2(6.7 h)＜S3(7.1 h)＜S4(7.2 h)，但开始变化与达到饱和的时间间隔为：S1(5.6 h)＞S2(5.0 h)＞S3(4.3 h)＞S4(3.9 h)。这是因为犁底层容重越大，该土层对湿润锋的吸力越大，湿润锋会暂停在容重突变界面，随着水分的不断下渗，吸力减弱，土壤水分才进入下层土壤中；同时，犁底层容重越大，该土层θs越低，土壤达到饱和所需灌水量越少，犁底层土壤入渗率达到稳定(最大)所需时间越短，故下层土壤达到饱和所需时间越短。

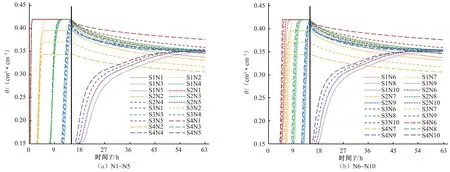
图2 各情景滴头位置N1～N5和2滴头中间N6～N10处θ变化曲线Fig.2 Dynamic changes of θ at N1～N5 at emitter position and N6～N10 between the two emitters in each scenario

2.1.2 湿润锋动态变化

图3显示各情景左侧滴头湿润锋随时间动态变化。随灌水时间增加，各情景湿润锋水平和垂直推进距离均逐渐增加。滴灌后期，模型边界土壤水分垂直运移速度明显增加，这是滴灌和不透水边界共同作用的结果；随滴灌进行，2滴头湿润锋发生交汇，图3中右侧交汇区土壤水分运移速度较左侧明显增加。湿润锋垂直推进距离主要表现出3 个阶段：各情景前3 h 湿润锋垂直推进距离基本相同；第4～7 h 随犁底层容重增加而降低；9 h 后随犁底层容重增加而增加；湿润锋水平推进距离表现出2 个阶段：前3 h 基本相同，之后湿润锋水平推进距离或模型边界垂直运移深度均随犁底层容重增加明显增加。有研究发现微润灌溉土壤容重越大，湿润锋向下运移速度越慢[26]，沙土中的黏土夹层可以减小湿润锋的垂直推进速度[27]，这均与本研究有相似之处。

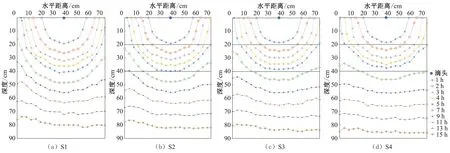
图3 湿润锋动态变化Fig.3 Dynamic changes of wet front

2.1.3 犁底层容重对土壤盐分运移规律的影响

图4 为各情景N1～N5、N6～N10 土壤水矿化度随时间变化规律。随土层深度增加，滴头位置剖面土壤水矿化度开始变化时间不断变长，且最大值不断降低。犁底层容重越大，滴头下方N2～N4 土壤水矿化度越低，2 滴头中间N6～N10 土壤水矿化度越高。其原因为犁底层阻碍土壤盐分随水分垂直运动，促进其水平运动，容重越大效果越明显，有学者通过沟灌研究发现，土壤容重越大，盐分运动受到的阻碍越强[28]。各情景耕作层N1和均质条件犁底层N2处土壤水矿化度均在灌水结束前达到入渗水矿化度，之后一直维持不变，S2～S4模拟时段内犁底层N2 处土壤水矿化度最大值分别是S1(3.0 g/L)的97.67%(2.93 g/L)、95.33%(2.86 g/L)和93.67%(2.81 g/L)；底土层N3 和N4 在灌水结束前后均有增长，S1 底土层N3 处土壤水矿化度最大值(2.86 g/L)分别是S2～S4 的1.05(2.73 g/L)、1.08(2.64 g/L)和1.16 倍(2.59 g/L)。对比2 滴头中间剖面：各情景耕作层N6 处土壤水矿化度最先开始变化，但观测后期却低于犁底层N7 处。其原因为犁底层容重越大，灌溉水到达犁底层后在耕作层及犁底层交界面的横向运动速度越快，由于“盐随水动”的特性，N7处土壤水矿化度增加越快。

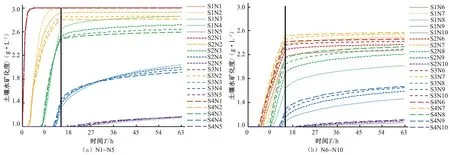
图4 各情景滴头位置N1～N5和2滴头中间N6～N10处土壤水矿化度变化曲线Fig.4 Dynamic changes of soil water salinity at N1～N5 at emitter position and at N6～N10 between the two emitters in each scenario

2.1.4 土壤水矿化度空间分布

模拟结束时土壤水矿化度等值线如图5所示。可以看出，受微咸水膜下滴灌影响，滴头下方土壤水矿化度最高，因此在含盐量较低土壤中用微咸水膜下滴灌时，土壤盐分会优先在滴头下方聚集。犁底层显著影响土壤水矿化度等值线，土壤水矿化度高值区垂直分布深度随犁底层容重增加明显减小，水平方向则随犁底层容重增加而增加，可见犁底层具有和黏土夹层一样的隔水滞盐作用[29]。有研究发现土层之间的渗透性差异越大，黏土夹层的滞盐作用越强[30]。本研究中犁底层容重越大，盐分往深层运移越慢。滴头下方土壤水矿化度变化界面深度均约90 cm，但2 滴头中间变化界面存在差别，表现为随犁底层容重增加而增加，但均小于滴头下方土壤水矿化度。不过也有学者研究发现犁底层土壤盐分含量较耕作层显著增大[13,31]，这是长期往复灌溉和蒸发多种因素综合作用的结果。

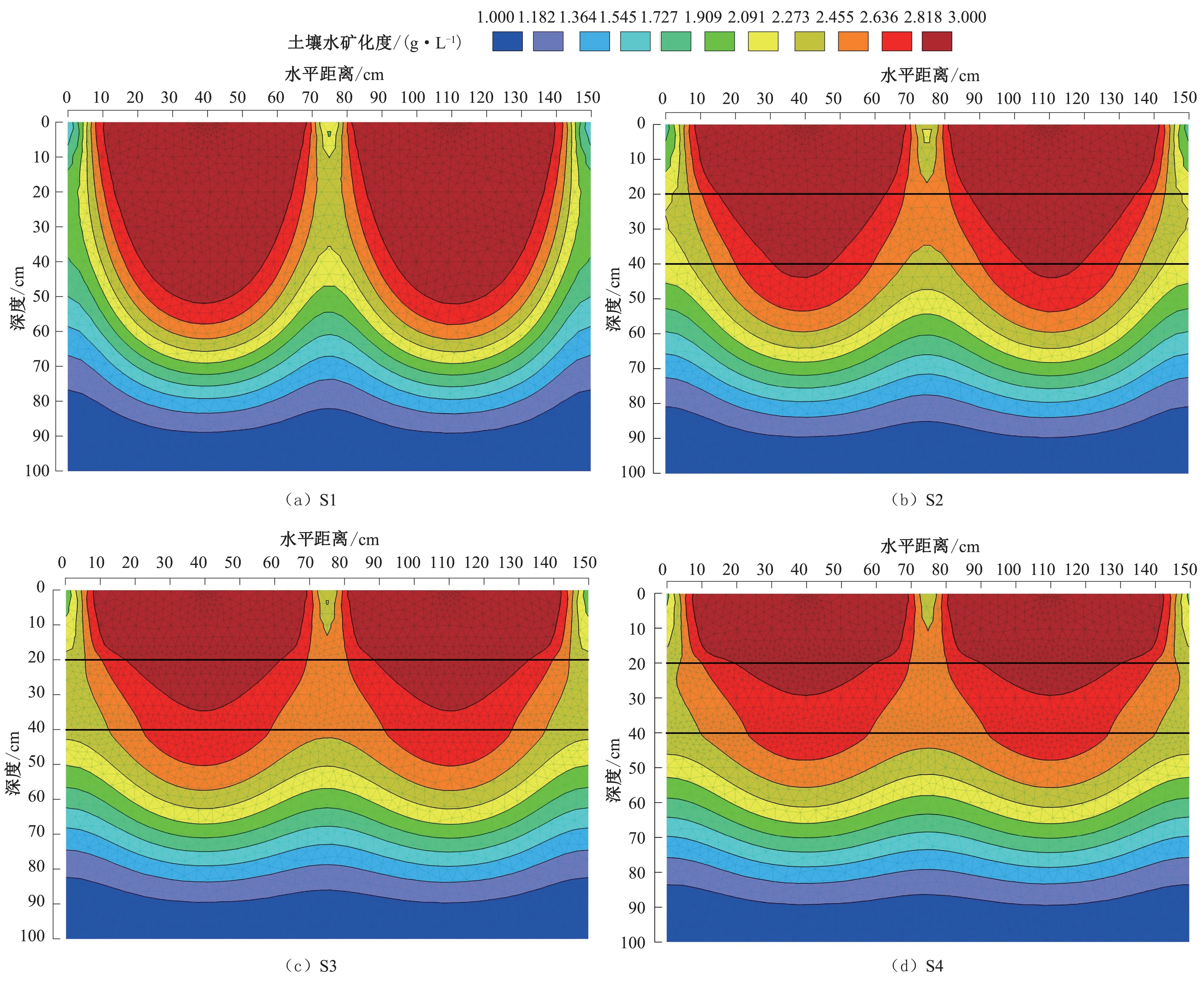
图5 模拟结束时土壤水矿化度空间分布Fig.5 Spatial distribution of soil water salinity at the end of the simulation

2.2 敏感性分析

根据上文定义的敏感度指数，计算土壤水盐对各参数的敏感度指数L（见表3）。从表3 中可以看出，θ对各参数的敏感度指数大于土壤水矿化度。θ对各参数的敏感度指数为：θs＞n＞Ks，土壤水矿化度对各参数的敏感度指数为：θs＞n＞αL＞Ks。敏感度指数L大于1，说明参数对输出变量的影响大；L小于1，说明参数对输出变量的影响小[32]。土壤水盐对4 个参数的敏感度指数均小于1，说明其影响较小。

表3 土壤水盐敏感度指数Tab.3 Soil water and salt sensitivity index

2.3 土壤水盐空间变异分析

2.3.1 土壤含水量空间变异分析

由于灌水结束时0～60 cm 深度θ处于饱和状态，故仅对灌后重分布48 h 土壤水分进行统计分析(见表4)。重分布48 h，耕作层θ均值随犁底层容重增加而增加(p＜0.05)；犁底层θ均值虽然逐渐降低，但其Se分别为79.61%、80.65%、83.05%和87.02%，随犁底层容重增加而增加(p＜0.05)；S2～S4 底土层θ均值随犁底层容重增加而降低(p＜0.05)，故犁底层不仅对本土层土壤水分重分布产生重要影响，而且会产生异位影响。各情景θ变异系数随土壤深度增加而增大；S4各土层变异系数最低(S3 和S4 耕作层均为0)，S1 各土层变异系数最大，故犁底层容重的增加可以降低本层及相邻土层θ的空间变异程度。变异系数可以反映样本的空间变异性，低于10%为弱变异，10%～100%为中度变异，大于100%为强变异[33]，各情景θ变异系数远小于10%，均为弱变异。

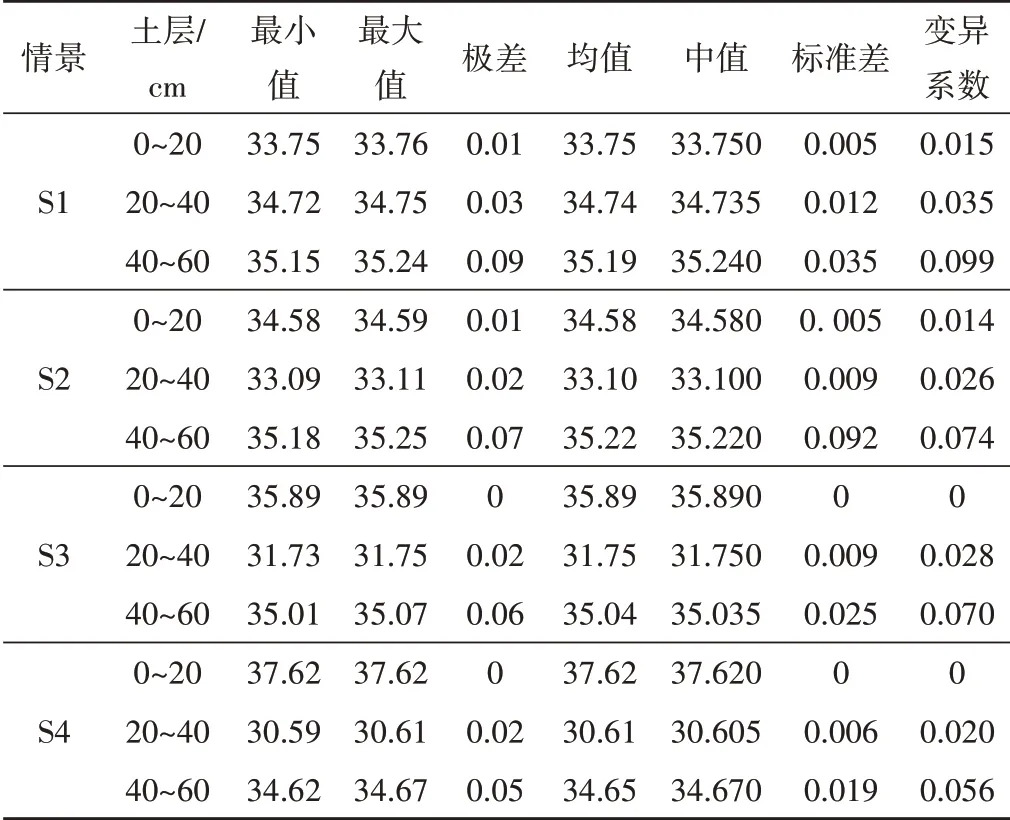
表4 模拟结束时土壤水分统计特征值 %Tab.4 Statistical characteristic value of soil moisture at the end of simulation

2.3.2 土壤水矿化度空间变异分析

表5 为灌水结束及重分布48 h 后土壤水矿化度统计特征值。随犁底层容重增大，各土层土壤水矿化度最小值逐渐增大，而犁底层和底土层最大值逐渐减小。各情景土壤水矿化度均值表现为：耕作层＞犁底层＞底土层，耕作层土壤水矿化度均值随犁底层容重增加而增加，S2～S4 和S1 的差异均达显著水平(p＜0.05)。有研究发现，上层土壤盐分与下层土壤容重正相关[14]，这与本研究中犁底层对耕作层土壤水矿化度的影响结果一致；但层状土壤中的黏土夹层在抑制表土积盐的同时会增加本土层含盐量[9]，而本研究中犁底层的土壤水矿化度却低于均质条件相同位置，可能原因是土质不同及本研究未考虑蒸发和地下水的影响。灌水结束时，S1 土壤水矿化度变异系数随土层深度增加而增加，但其余情景犁底层位置最低，且各土层土壤水矿化度变异系数随犁底层容重增加而降低；S4 耕作层、犁底层和底土层土壤水矿化度变异系数分别是S1 相同土层的61.92%、35.05%和35.51%，因此，犁底层能够显著降低土壤盐分的空间异质性。重分布48 h，各情景各土层土壤水矿化度最小值、最大值、均值有不同程度的增长或不变，且增长量随土层深度增加而增加；S2～S4 和S1 耕作层土壤水矿化度均值差异仍达到显著水平(p＜0.05)；各情景各土层土壤水矿化度变异系数较灌水结束时均有所降低，但降低幅度随犁底层容重增大而减小。

表5 灌水结束时(模拟灌水时长15 h)及重分布48 h后(模拟时长63 h)土壤水矿化度统计特征值 g/LTab.5 Statistical characteristic values of soil water salinity after irrigation and 48 hours'redistribution

2.4 犁底层容重对排水排盐的影响

4 种情景模拟结束时累积排水排盐量见表6。S4 累积排水排盐量最大，其次是S3，而S1 最小；灌水结束时，犁底层容重越大，透过犁底层到达底土层的水量越大（见图3），底土层排出的水量越多，但犁底层上部土层的下渗水量越少。在本研究的特定情境下，受犁底层的影响，多透过犁底层的水量大于犁底层导致的上部土层减渗的水量，且其影响随容重增加而变大，故犁底层容重越大，模型底部累积排水排盐量越大(p＜0.05)。S1 和S4 累积排水量差为32.157 cm3/cm，远小于模拟结束时犁底层容重对本土层产生的水量差异（124.2 cm3/cm，犁底层面积×模拟结束时两情景犁底层位置θ之差），各情景排水矿化度随犁底层容重增加而增大，但远小于滴灌用水矿化度。

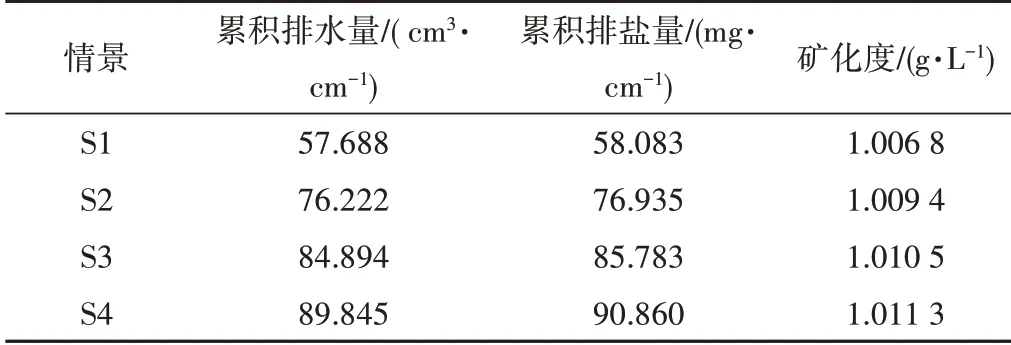
表6 各情景模拟结束时排水排盐量Tab.6 Drainage and salt discharge at the end of simulation

通过将矿化度作为溶质示踪剂，发现排水中新水所占比例很小(见表7)，且该比例随犁底层容重增大而略有增加。有学者通过同位素技术和溶质示踪剂揭示降雨前储存在土壤中的老水是降雨径流的主要来源，而雨水主要起驱遣老水的作用[34]。基于本研究的模拟域及灌溉情景，灌溉水会驱使背景矿化度较低的土壤水排出，而矿化度较高的灌溉水会滞留在土壤中；故对于不受盐碱化影响或盐碱化程度较轻的农田，使用矿化度较低的微咸水进行灌溉仍会加重土壤盐碱化程度。

表7 排水来源百分比 %Tab.7 Percentage of drainage water

3 结论

本文通过Hydrus-2D软件模拟犁底层容重对微咸水膜下滴灌土壤水盐变化、统计特征值及排水排盐的影响，得出以下主要结论。

（1）在相同土质和滴灌条件下，犁底层容重越大，耕作层土壤水流横向渗流扩展能力越强，土壤水分下渗速度越慢，底土层含水量变化所需时间越长。犁底层对湿润锋垂直推进距离的影响表现为先抑制后促进，而水平方向一直为促进。犁底层显著影响土壤水矿化度空间分布，该层容重越大，滴头下方土壤水矿化度越小，2滴头中间越大。模拟结束时累积排水排盐量随犁底层容重增大而增大(p＜0.05)。通过将矿化度作为溶质示踪剂发现，所排水量中灌溉水所占比例很小，且随犁底层容重和累积排水量的增加而增加。

（2）灌水结束时，各情景土壤水矿化度均值随土层深度增加而降低；均质条件土壤水矿化度变异系数随土层深度增加而增加，但其余情景犁底层最低，且各土层土壤水矿化度变异系数均随犁底层容重增加而降低。重分布48 h，各情景土壤水矿化度变异系数较灌水结束时均有所降低，但降低幅度随犁底层容重增大而减小。

（3）本研究仅考虑了犁底层容重对微咸水膜下滴灌土壤水盐运移分布的影响，未考虑蒸发、地下水、植被与犁底层的耦合影响规律。应用本文研究成果时，还需根据田间具体条件开展相关试验对数值模型参数进行进一步率定，并在必要时完善模型结构。