多干扰源下热连轧机主传动系统扭振问题研究

张义方,崔 立,何 成,李 聪,朱小龙

(1.上海第二工业大学 智能制造与控制工程学院,上海201209;2.安徽工业大学 机械工程学院,安徽马鞍山243000)

0 引言

热连轧机轧制薄规格带钢的产业在整个钢铁行业中处在上游关键地位。然而截至目前,连轧机异常振动问题仍未得到彻底解决,扭振失稳现象的频繁发生降低了带钢产品整体质量及生产效率。轧机系统是机-电-液系统相结合的多耦合复杂一体化系统,涉及学科广泛,复杂非线性因素在轧机系统中普遍存在,引起扭转振动问题,降低连轧机系统的稳定性[1-4]。目前已有众多国内外学者就其耦合特性从不同角度对轧机系统振动问题进行研究,取得丰硕成果[5-9]。主传动系统中辊系所在的垂直系统非线性因素复杂,不仅存在液压系统非线性因素[10],也存在结构、摩擦、间隙等非线性因素的影响[11-13],且板带振动激励[14],辊间接触非线性[15]等都会产生谐波激励导致辊系负载扰动。有学者就辊系负载扰动对主传动系统的耦合扭振问题进行了仿真分析,并取得一定的进展[16]。电动机作为主传动系统的驱动端,一些学者从该角度出发,发现电动机内部非线性因素所产生的扰动力矩会使主传动系统发生扭振[17],也有学者通过现场实测分析发现电气系统特征频率与主传动系统固有频率接近时会引发机电耦合共振现象[18]。理想情况下,稳态轧制时电机驱动力矩与负载力矩达到平衡,然而在干扰普遍存在的情况下,实际生产中理想情况难以实现,通常电机力矩扰动及负载力矩扰动会协同作用于连轧机主传动系统,产生更加丰富的扭转共振现象,值得更加深入的研究。

综上,本文考虑将电机谐波扰动及负载谐波扰动共同作用于轧机主传动系统,建立含非线性刚度及非线性阻尼的主传动系统扭振动力学模型,以某钢铁企业1 580 mm热连轧机F2轧机主传动系统为研究对象,分析实际振动信号特征,并结合理论对连轧机主传动系统非线性扭振特性机理进行深入分析探究。

1 问题分析

某钢企1 580 mm热连轧机在轧制薄规格带钢时出现剧烈振动现象,尤其以F2轧机振动最为剧烈,使用信号采集分析系统分别对主传动系统接轴扭转振动信号、轧机电机尾部、电气系统接入电流信号、轧机机座处等进行信号测试,其波形时谱及快速傅里叶变换(Fast Fourier Transform,FFT)频谱如图1～4所示。

从图1中可以看出,上扭矩波形时谱中明显的“拍振”规律,且频谱中含有其典型的41.65 Hz扭振特征频率。图2中电机尾部振动加速度信号可以看出其振动特征频率与上扭矩特征频率较为接近,可能存在机电耦合共振,且从图3中电流信号频谱中也存在与其较为接近的特征频率幅值峰,更增加了这种可能性。图4中轧机机座处振动信号主要的低频特征频率与主轴扭振特征频率较为接近,有理由怀疑轧制负载端的共振扰动对主传动系统有耦合共振的可能。

图1 上扭矩振动信号时的频谱Fig.1 Time and frequency spectrum of upper torque vibration signal

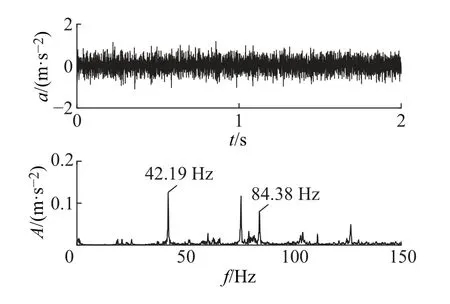
图2 电机尾部加速度时的频谱Fig.2 Time and frequency spectrum of motor end acceleration

图3 系统接入电流信号时的频谱Fig.3 Time and frequency spectrum of current signal in the system

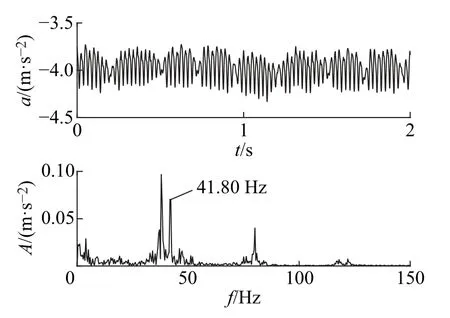
图4 轧机机座处波形时的频谱Fig.4 Time and frequency spectrum of mill stand

从图1～4中频谱图中存在的大量谐波也说明了存在非线性因素的影响。通过以上分析可知,研究电机谐波力矩及负载谐波力矩多干扰源下的主传动系统扭振特性进行很有必要。

2 连轧机主传动系统扭振模型

2.1 主传动系统扭振等效模型

考虑易于求解及等效原则,将连轧机主传动系统中电机、轧辊及中间各元件构成的系统组合体视作二质量系统[19],如图5所示。图中M1、M2分别为等效二自由度模型的电机转矩及辊系负载转矩;J1、J2分别为电机及轧辊转动惯量;θ1、θ2分别为电机转子与轧辊转动角度;k、c分别为连接轴刚度及阻尼。

图5 主传动系统等效二质量扭振模型Fig.5 Equivalent two mass torsional vibration model of main drive system

根据能量守恒及Lagrange动力学原理,建立考虑非线性刚度项及非线性阻尼项的主传动系统扭振非线性动力学方程为:

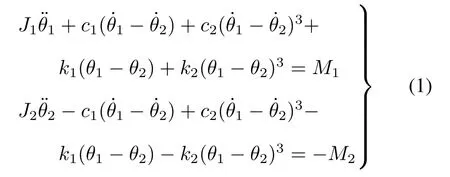
式中:θ1、θ2分别为电机及轧辊的初相角;c1、c2分别为线性阻尼项和非线性阻尼项系数;k1、k2分别为线性刚度项和非线性刚度项系数。又

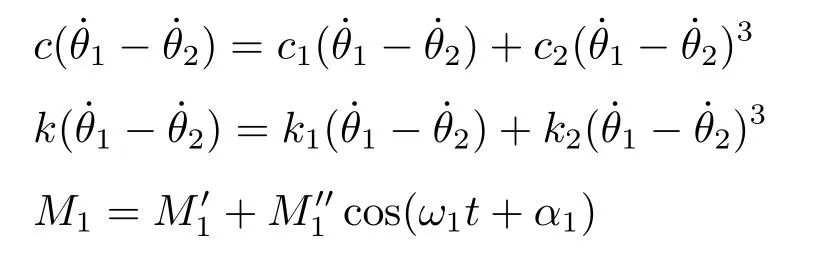
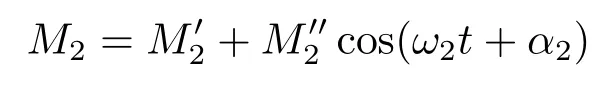
ω1、ω2为电机和轧辊的角速度;为稳态下电机及轧辊转矩,且稳态时有分别为电机谐波扰动转矩以及轧辊负载谐波扰动转矩。设φ1、φ2分别为其对应扰动转角,并考虑稳态匀速情况下将前述关系代入式(1)后并整理得:

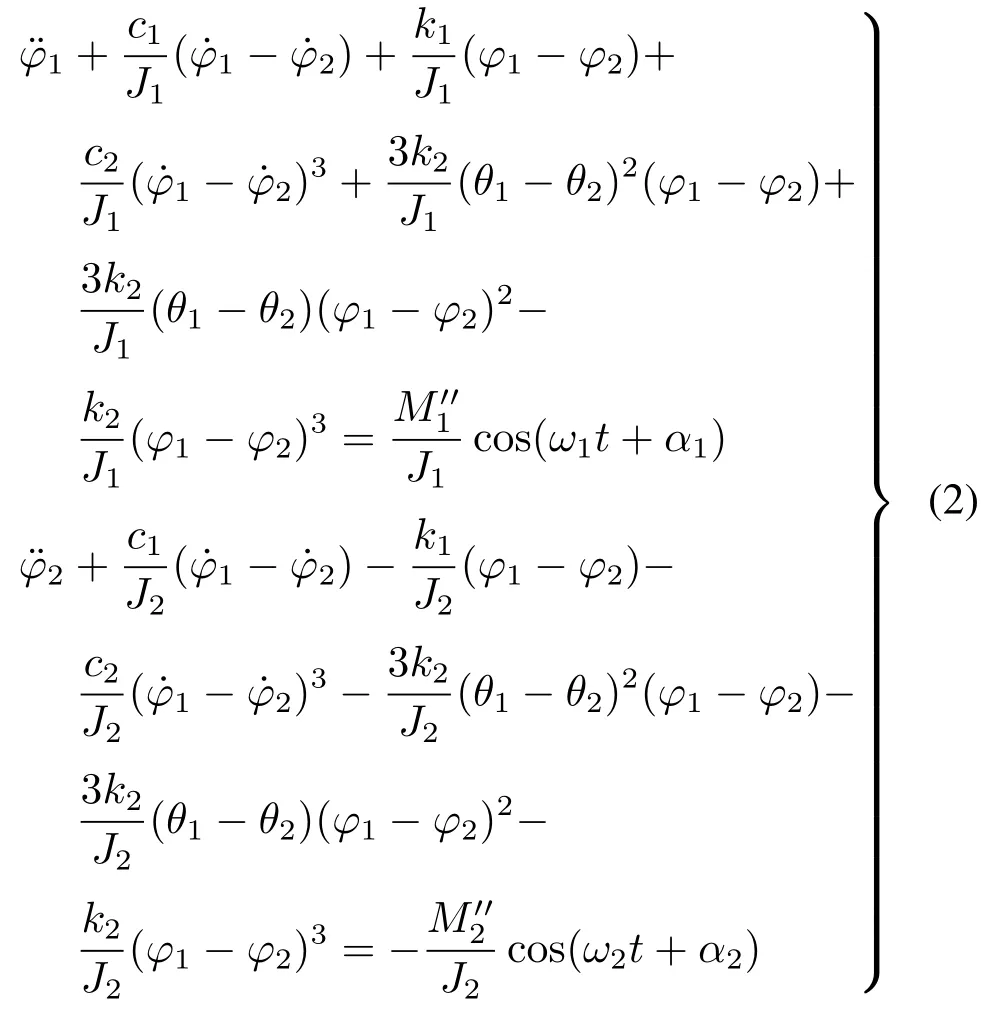
上下两式相减并化简,并令u=φ1−φ2,得到电机谐波扰动和负载谐波扰动共同作用下的系统扭振非线性方程为

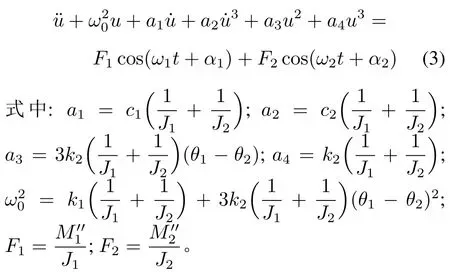
2.2 非线性方程求解

本文使用多尺度方法[20]对非线性方程进行求解。引入小参数ε,式(3)可化为

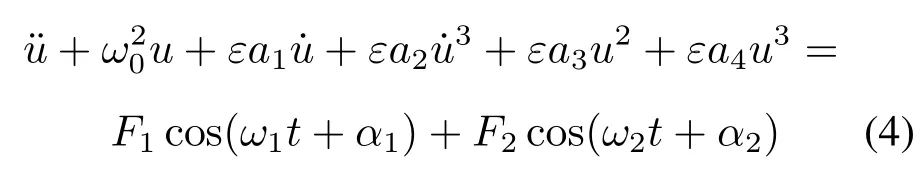
设方程近似解析解

T0,1分别为慢、快尺度时间,并将微分算子D0=代入式(4)后比较ε0,ε1项系数得:

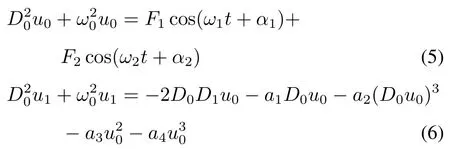
将式(6)的解写为复数形式

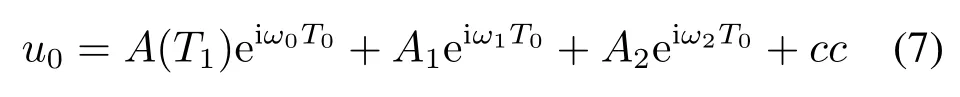
式中:A为自由振动幅值;A1,2为受迫振动幅值;cc为前面各项共轭项。且

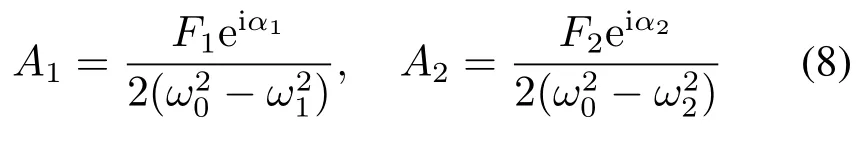
将式(7)、(8)代入式(6)(公式略),得到非线性扭振系统理论上存在的共振模式如下:

2.3 共振幅频响应求解

2.3.1 1/2倍亚谐波共振响应求解

考虑系统1/2倍亚谐波共振情况,引入调谐参数σ,设ω1与ω0的差别为ε的同阶小量,写为ω1=2ω0+εσ,σ=o(1),ω2远离ω1基频及倍频,满足消除久期项的条件为

将A写为指数函数形式

将式(10)代入式(9),得

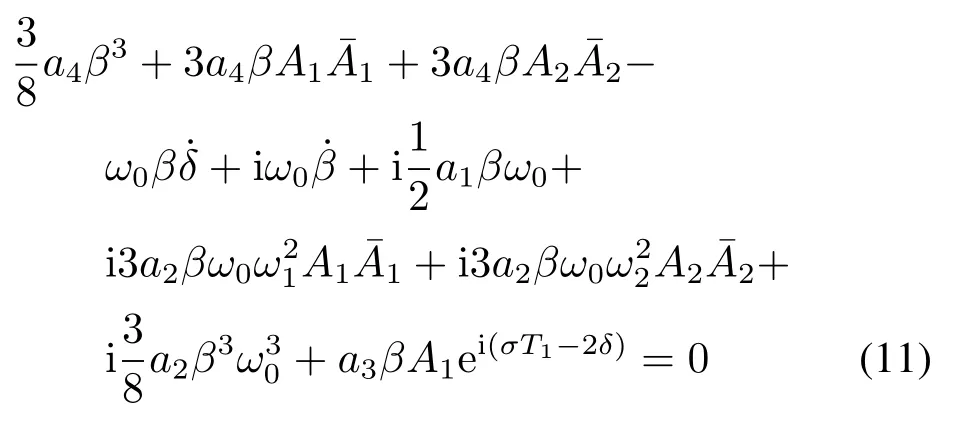
分离实部虚部得

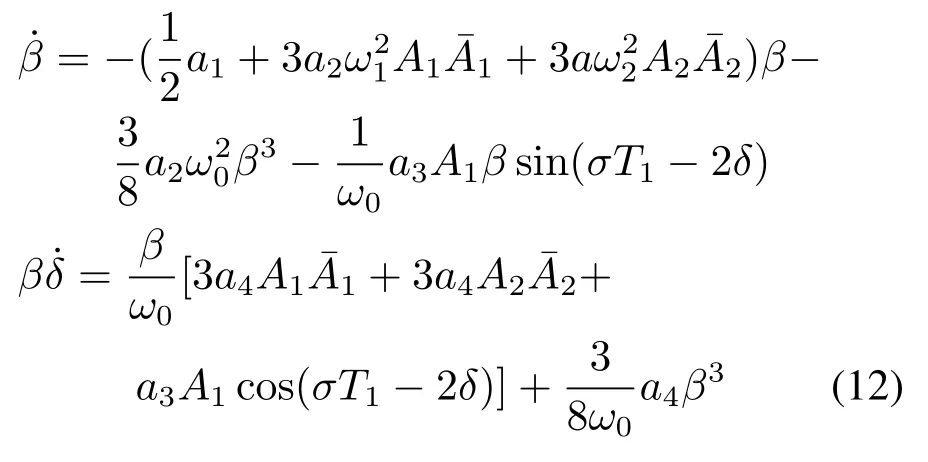
令θ=σT1−2δ,代入式(12)并化简得

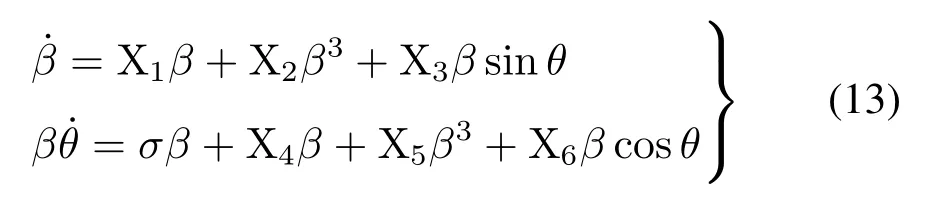
式中:

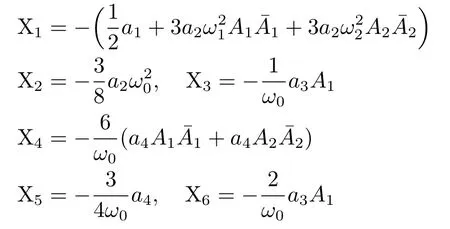
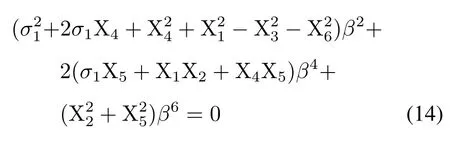
2.3.2 倍超谐波共振幅频响应求解

考虑系统2倍超谐波共振情况,引入调谐参数σ,设2ω1与ω0的差别为ε的同阶小量,写为2ω1=ω0+εσ,σ=o(1),ω2远离ω1基频及倍频,满足消除久期项的条件为

将式(10)代入式(15)化简得

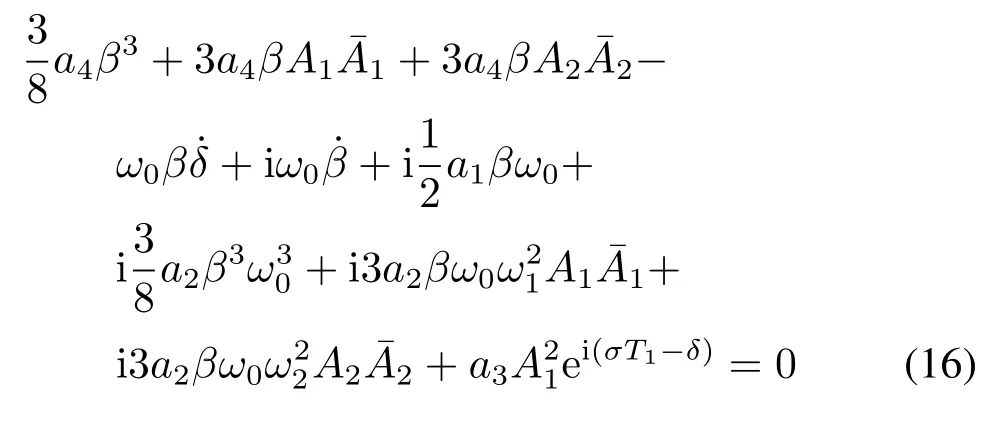
分离实部虚部得

令θ=σT1−δ,得到

其中:

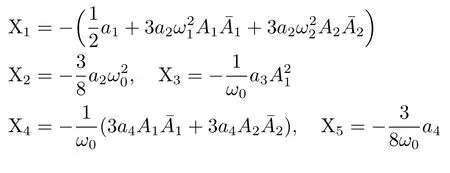
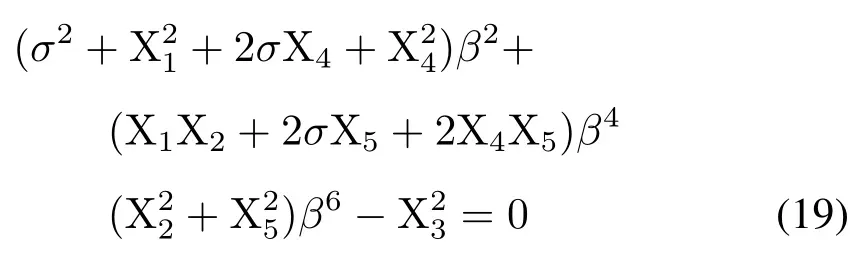
2.3.3 组合共振幅频响应求解

考虑ω1ω2≈ω0组合共振形式,引入调谐参数σ,令ω0=ω1+ω2−εσ,σ=o(1),满足消去久期项的条件为

将式(10)代入式(20)化简得

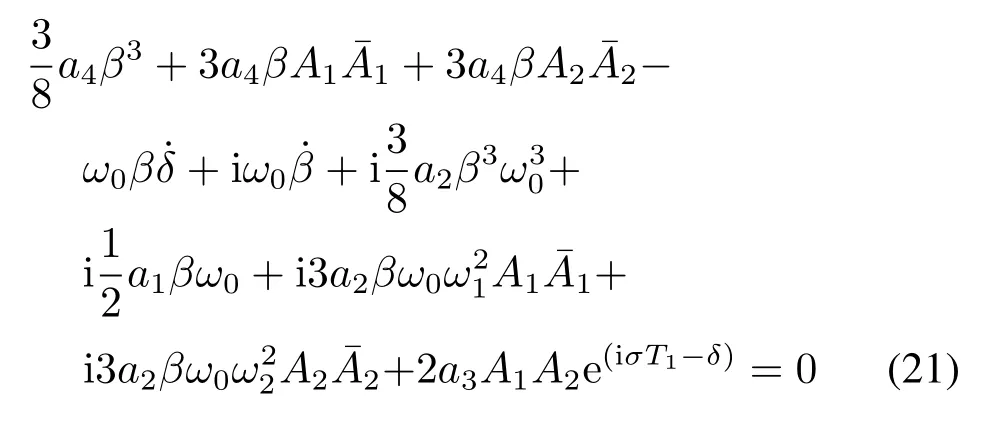
分离实部虚部并化简得

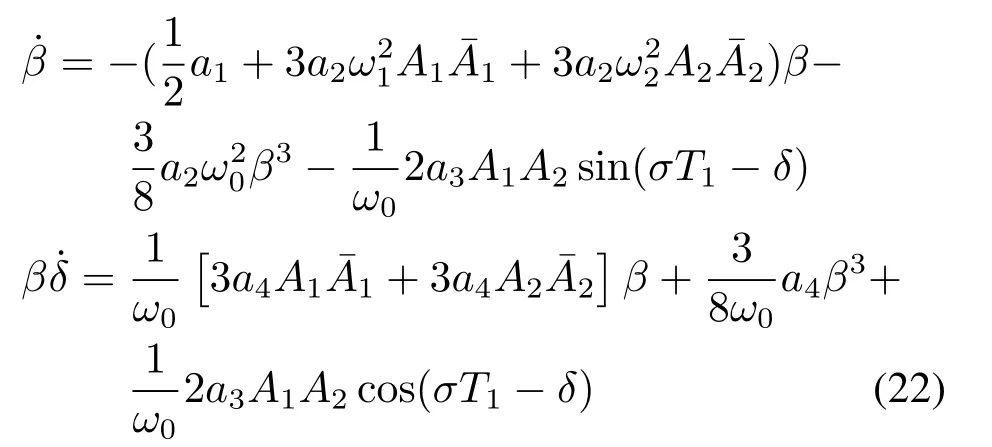
令θ=σT1−δ,代入式(22)得

式中:

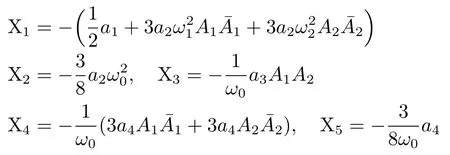
3 算例仿真分析

依据某钢铁企业实际参数等效得到:J1=1.05×104kg·m2,J2=7.96×102kg·m2,k1=5.48 MN·m/rad,=3 kN·m,=4 kN·m,其中为利用等效原则获得的轧机电机转子、传动轴及减速机的等效转动惯量;J2为轧辊、中间接轴及齿轮座的等效转动惯量;k1为主传动联结轴、中间接轴的等效刚度;和为通过轧机在线采集系统监测获得的电机驱动和轧辊谐波扰动力矩。

利用连续小波变换方法[21-22]对实测咬刚衰减信号进行参数辨识得到辨识参数:c1=7.04 kN·m·s/rad,c2=−4.81 kN·m·s3/rad3,k2=−456 kN·m/rad3。分别将这些参数计算并代入各共振幅频响应方程,通过改变一个参数并固定其他参数不变可得到不同参数下幅频响应变化曲线。

3.1 1/2倍亚谐波共振分析

将参数计算并代入方程(14),调整非线性刚度参数数值大小,得到不同数值下得幅频曲线见图6。由图6(a)可知,系统在“软弹簧”特性下,非线性刚度项对系统影响较为明显,随着非线性刚度数值逐渐减小的过程中,中心频率左移明显,幅值逐渐增大,曲线左偏程度逐渐加大,共振域逐渐变宽,不稳定区域也随之增大,幅值跳跃程度逐渐增加。图6(b)为通过调整非线性阻尼项,固定其他参数不变得到的幅频响应变化曲线,在非线性阻尼逐渐增大的影响下,其扰动幅值增大较为明显,但对中心频率影响甚微,对共振域影响也极小。图6(c)中展现了在电磁谐波力矩不断变化时幅频响应曲线的变化。通过曲线可见,电磁谐波力矩大小对幅值及共振域的影响均较为明显,扰动力矩增大,幅值也增大,共振区域也增大,此时系统可能发生机电耦合共振的几率增大,针对此种情况在实际系统可考虑减小电磁谐波力矩幅值来达到减小振动幅值的目的。图6(d)中曲线表明线性阻尼仅对幅值有影响,对共振区域,曲线弯曲程度骨干线均无明显影响。且随着线性阻尼的增大,幅值降低,因此可以考虑调整线性阻尼大小进而调整扰动幅值提高系统稳定性。

图6 1/2倍亚谐波共振幅频响应Fig.6 Amplitude frequency response of 1/2 times subharmonic

3.1.1 倍超谐波共振分析

将参数代入式(19),得到图7所示2倍超谐波共振幅频响应曲线。从图7(a)可知,系统在“软弹簧”特性下,非线性刚度项对系统共振幅值、共振区域,中心扰动频率偏移均有较大影响。随着非线性刚度项的减小,系统扰动幅值随之增大,曲线左弯幅度加剧,共振区域增大,系统不稳定跳跃程度加剧。

图7(b)曲线为固定其他参数不变,调整非线性阻尼项得到的系统幅频响应变化曲线,由图可知,随着非线性阻尼数值的增大,系统扰动幅值随之增大,但对共振区域及曲线骨架弯曲程度影响微乎其微。图7(c)所示为调整电磁谐波力矩大小所得出得超谐波共振幅频响应变化曲线,由图可见,电磁谐波扰动力矩对系统在超谐波共振下的扰动幅值、共振域、骨架曲线弯曲程度等均有较大影响,数值减小后,虽幅值有所降低,但共振域却剧烈增大,提高了系统发生机电耦合共振的风险。图7(d)为线性阻尼变化对系统幅频响应的影响变化曲线,由图可见,线性阻尼项主要影响系统扰动幅值,其共振区域及曲线骨架弯曲程度影响稍小,随着线性阻尼数值的增大,系统扰动幅值稍有提高。

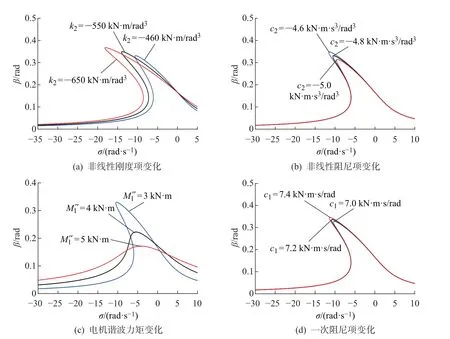
图7 2倍超谐波共振幅频响应Fig.7 Amplitude frequency response of 2 times superharmonic resonance

3.2 组合共振幅频响应曲线

将计算等效参数代入式(24)得到图8所示的ω1+ω2≈ω0组合共振模式下幅频响应变化曲线,通过固定其他参数不变,调整一个参数值得到不同参数影响下的幅频响应曲线变化。图8(a)为固定其他参数不变,调整非线性刚度项数值得到的软式非线性系统幅频响应曲线。由图可见,非线性刚度项变化对系统共振区域影响较大,对扰动幅值及骨架曲线弯曲程度影响相对较弱。随着数值的减小,共振区域明显增大,幅值稍有增加,骨架中心频率左移明显。图8(b)为非线性阻尼项变化下的组合共振幅频响应曲线,由图可以看出,在非线性阻尼项数值逐渐提高的过程中,幅频响应曲线幅值稍有增大,对共振区域及骨架曲线的弯曲程度的影响微乎其微。

图8(c)所示曲线为电磁力矩扰动作用下的组合共振幅频响应曲线。由图可以看出,电磁谐波力矩对系统共振域、幅值等的影响均较为明显,对骨架线弯曲程度影响相对较小。随着电磁谐波力矩的增大,扰动幅值增大,共振域也随之增大。图8(d)显示出线性变化对系统扰动幅值及共振域影响均较为轻微,随着数值的提高,扰动幅值有较为微弱的增大,对骨架曲线及共振区域的影响则更微乎其微。

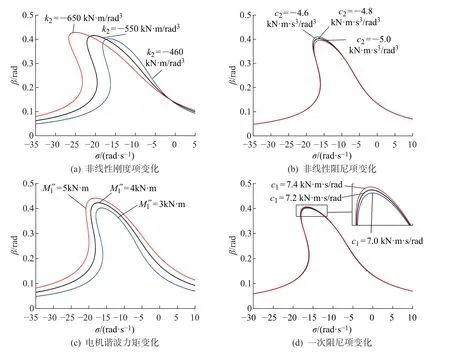
图8 ω1+ω2组合共振幅频响应Fig.8 Amplitude frequency response of combinedω1+ω2

从以上分析可以看出热连轧机主传动系统的动力学特性受非线性刚度及电磁谐波力矩的影响较大,轧机主传动刚度参数可以通过修改传动设备结构尺寸参数来完成,电磁谐波力矩可以通过优化变频器参数来进行。

4 结 语

针对热连轧机异常振动问题,通过分析某钢企1 580 mm热连轧机F2机组主传动系统实测振动信号,发现系统可能存在特征频率耦合共振并且存在大量非线性谐波分量,针对该问题建立了包含非线性阻尼、非线性刚度项的二自由度主传动系统非线性动力学模型,研究系统在电机谐波扰动及负载谐波扰动多干扰源下的共振问题,得出以下主要结论:

(1)针对主传动系统建立了二质量系统等效物理模型及主传动系统扭振动力学数学模型。

(2)运用多尺度法求解出了非线性扭振动力学系统的包括1/2倍亚谐波共振、2倍超谐波共振及ω1+ω2≈ω0在内的极为丰富的共振模式,并分别求得其亚谐波、超谐波、组合共振的幅频响应方程。

(3)根据轧机实际参数,通过数值仿真分析在非线性刚度、非线性阻尼、电机谐波力矩及线性阻尼下对系统影响的幅频响应曲线,发现系统在非线性刚度及电机谐波力矩对各类共振模式下的扰动影响均较大,阻尼一次项对系统扭振影响则相对较弱。在抑制扭转振动方面,可以从修改设备结构尺寸和优化变频器参数来进行分析。