基于地物消长零和律的地物演化机制

钟业勋,胡宝清,栾俊,叶彤

(1.海军工程大学 导航工程系，湖北 武汉 430043；2.南宁师范大学 北部湾环境演变与资源利用省部共建教育部重点实验室，广西地表过程与智能模拟重点实验室，广西 南宁 530001；3.海军参谋部海图信息中心，天津 300450)

0 引言

人类行为总有某种目的。价值观念总会在科学探索中体现。种种意识行为，如我们国家或各地区种种规模不同的规划设计项目，从高铁的纵横交错到各类建设的日新月异，从城镇的快速发展到扶贫措施的落实，都是人类主体意图的体现。所谓主体意图，就是未来实践过程及结果的先期规划，是存在于主体之内的超前表象，是具有指导实践作用的观念模型[1-3]。把主体意图变为人类期望的现实，是地物演化的主流因素。由自然原因引发的水旱灾害、火山、地震、泥石流等自然灾害和灾后重建，以及按人类主体意图实现的各类工程实体，都会使相关区域的地物地貌发生变化。人类认识世界需要地图，地图也是人类改变世界的成果[4]。从今天快速更新的地图总是赶不上现实变化的状况，也可反观制图区域，特别是经济发达地区地物变化之快速。这种宏观变化非常普遍。文献[5]探讨过地物演化的物理基础，文献[6]对地图现势性的机理进行过研究，而地图现势性则为制图区域地物变化的反映和表达，地图现势性是地图反映制图区域真实性程度的表征。我国的资源三号卫星，可对地球南北纬84°以内的地区实现无缝影像覆盖，对我国领土和全球范围的一次影像覆盖只要59 d。资源三号卫星的影像资料，可用于1∶50 000及更大比例尺地形图的修测与地理信息更新[7]。虽然监测地表变化的手段已相当先进，但关于地物演化机理的文献似乎鲜见，导致这方面的理论研究落后于现实的需要。鉴于地物演化的普遍性和了解演化、掌握变化对人类自身生存和可持续发展的重要性和必要性，笔者根据地物演化必须遵循地物消长零和律的规则，应用点集拓扑学的原理，对地物演化的机制进行研究和探讨。

1 空间、时间和物理现象的密切关系

空间和时间是物质的存在形式。时间是物质运动的连续性、间断性和延续性。时间是天体及其物体的自然属性，今天过了就是明天，但今天不可能退回到昨天，这是时间的不可逆性，是天体运动的不可逆性的印证。时间只有过去、现在、将来的时态之分。空间是物质的广延性和伸张性，是一切物质系统中各个要素的共存和相互作用的标志[8]。人类活动是一种时空行为。世界上各种自然和社会现象的发生及其发展和演化，都是在一定的时间和空间进行的[9]。现代科学界的极限空间长度是普朗克长度d0=1.62×10-35m，小于普朗克长度，对现有的空间概念不再适用。极限的时间间隔是普朗克时间间隔s0=5.39×10-44s，小于普朗克时间间隔，现有的时间概念不再适用[10]。

空间，时间和物质存在的不可分割性原理，闵可夫斯基通过引入“四维连续区”来进行解释：所谓“四维连续区”是指三维空间x,y,z和一维时间t，空间存在中的三维坐标x,y,z必需大于普朗克长度d0，因为三维中任何一个为零，都会导致三项的乘积为零的结果，也就是

∀(x,y,z)∈v,如果(x=0)∨(y=0)∨(z=0)⟹v=0⟺物质v不存在。

(1)

(x×y×z)=v>0⟹(x>d0)∧(y>d0)∧(z>d0)。

(2)

体积v大于0等价于物质在三维空间中存在；根据物质在三维空间中存在与时间存在的不可分割性的逻辑推定，此时v的存在时间t必大于普朗克时间间隔，从而也得t>0。这样，三维空间中的“事件”就成为四维“世界”的“存在”。三维空间中的“事件”与四维时空的等价性质，本身就表达了物质空间存在与时间的不可分割性。据此可用谓词公式表达物质在四维时空中“存在”概念：

定义1三维空间中的事件 设K为三维空间，vi为性质为i∈I的事件，d0=1.62×10-35m为普朗克长度，s0=5.39×10-44s为普朗克时间间隔，则

∀(xi,yi,zi)∈vi，如果(xi>d0)∧(yi>d0)∧(zi>d0)⟹vi≠∅

⟹ti>s0⟹ti>0⟺∃vi∈K,

(3)

式(3)表明，三维空间中事物vi的存在导致ti>d0的必然结果，从而阐明了物质的存在与时间的不可分割性。说明空间非空性和寿命为非零实值是物质存在的充要条件[11-13]。

从定义1又可推论：

定义2任何空集的时间存在均为零。

∀(xi,yi,zi)∈vi,当(xi=0)∨(yi=0)∨(zi=0)⟹vi=∅⟹ti=0∈vi,

(4)

式(4)表达了这样一个事实：现实中不存在的任何事物，它的寿命恒为零。

如今科学界已认同宇宙中存在6种不同类型的夸克。夸克的空间尺度小于10-16m，而质子和中子则在10-16～10-15m。丁肇中在实验中测出电子直径至少是小于10-19m。这一切都表明，现今所发现的构成宇宙中一切物质的基本粒子，其空间尺度也都远大于空间概念适用的普朗克长度[14]。四维时空的关系表明，在空间中存在的物质都有对应的存在时间——寿命。z0粒子可谓是寿命最短的粒子，它的寿命也有10-25s，这个数值也远大于时间概念适用的普朗克时间间隔s0。空间存在物必有创生时刻也有消亡时刻。人和各种动物、植物，都有生有死，就连人赖以生存的地球，地球物理学家根据铅同位素也能测算出地球大约已演化了46亿年，所以科学界通常认为地球的年龄有46亿年，同时测出太阳系许多陨石以及月球的年龄也差不多是45亿～46亿年。现今地球上的海陆分布格局，也是从2亿年前联合古陆分裂演化来的。地球上看似没有生命的岩石，也有年龄，这就意味着它也有生成的时刻。同年龄的岩石其磁性方向相同，比如，0～70万年的岩石，其磁性方向以正方向为主；而70万～243万年的岩石，则有与前者相反的磁性方向[15]。

2 基于点集拓扑学的地物演化机制

2.1 拓扑变换、边界、闭包和状态的定义

定义3拓扑变换 设X与Y是两个随意的拓扑空间，并设f:X→Y,如果f是连续的双一一函数，并且它的反函数f-1也是连续的，那么，f就叫做空间X到空间Y上的一个同胚或拓扑映射或拓扑变换；此时空间X与空间Y叫做同胚，记作X≈Y。

定义4边界 设A是拓扑空间X的子集，x∈X,如果在x的任意邻域中既有A的点又有X-A的点，则称x为A的边界点。A的边界点全体所成的集合称为A的边界，记为b(A)。

(5)

可见A的导集A′就是A的边界：A′⟺b(A)。

状态是标志若干物理量的综合，而这种综合以单值的形式同每一个相继时刻的每一个相似的综合联系在一起。状态是指系统那些可以观察和识别的量、态势、特征等。状态变量x随时间而变化的系统，可以表示为时间t的函数，称为动态系统[17]。地物的演化本质上是不同性质的点集随时间消长，并改变不同点集间的关系和空间结构及外在特征的一种综合，它是随时间而变化的系统，因此，vi在时间进程中具有不同的占有空间,而且是时间t的函数。

定义6状态 ∃vi∈K∧t∈ti∈vi，若条件满足：

∀vi∈K∧ti=(t2-t1)∈vi⟹vi=vi(t)|t∈ti，

(6)

则称vi(t)为vi在t时刻的状态。

这种vi(t)随时间变化的例子极为普遍。一个人从出生时的婴儿到幼儿、儿童、少年、青年、中年、老年的演化过程，其状态差异十分明显。式(5)是空间中的非空存在物状态表达的通式。不同的vi有不同的状态演化特点。

2.2 地物消长零和律

根据点集的初始状态和经变换后的目标点集的状态关系，可定义点集变换的基本类型。

定义7消亡型点集

∃ei≠∅∈X,ti=(t2-t1)∈ei∧ei(t2)=∅⟹ei(t′)t,t,t′∈ti,

(7)

则称ei为消亡点集，满足式(6)的演化称为消亡型演化，记作Δ-型演化。

显然，(6)式表达了原来存在于X区域内的非空点集在时间中逐渐缩小直至消亡的过程。

定义8增长型点集

∃qk∉X∧qk(t1)=∅，tk=(t2-t1)∈qk⟹qk(t′)>qk(t)|t′>t,t,t′∈tk,

(8)

则称qk为新生点集，满足式(7)的演化称为增长型演化，记作Δ+型演化。

显然，式(7)是原来的区域X内并不存在的新生地物qk增长过程的模式。

定律1地物消长零和律 消亡地物伴生新地物的必然性、同时性、历时性、渐进性和消长代数和恒为零，称为地物消长零和律，即

∃ei∈Δ-∈X⟹∃qk∈Δ+∈Ys.t.(Δ-ei+Δ+qk)=0|i≠k∨i=k,

(9)

式中,qk便是由ei消亡而伴生的新地物，也是ei的覆盖。这是伴生必然性和同时性。这种新旧交替大部分属于异质(i≠k)的交替或覆盖，如qk为一高铁，它对下方地物的覆盖过程是同时的，因为修建高铁需要工期，所以具有历时性和渐进性。如果是旧房夷平后建新房，新旧更替的性质不变，是满足i=k的交替或覆盖。现实中，即使是i=k的情况，由于两者范围大小的差异，总会存在某些i≠k的地物被覆盖，因此完全满足i=k的演化非常少。地物消长零和律确保了地物演化空间的不变性或恒定性，这也是地物演化的铁律[18]。不同地物之间总存在着或明显或隐蔽的变界，通过边界的变动可以发现地物在时间中的演化。例如，洪水的涨落，其水面和陆地的界线变动就异常明显。地类性质的变更，也容易从相邻边界的变动中判断相关地物的扩、缩、消、长，由于演化空间的恒定不变，任何地物的缩小必定有等量的异质地物充实其空间，始终以代数和为零的规律确保演化空间的恒定性，这就是地物消长零和律。由于时空的连续性，使得地物的演化具有历时性。地物的演化，比如说某一地区，基于经济发展的需要，总要结合本地区的自然和人文条件作出相应的发展规划，包括道路规划、工业建设、文化建设等，要把这规划变成现实，都是需要建设工期的，所以，单项规划或总体规划的实现，也即新地物对旧地物的覆盖具有历时性和渐进性。

X上存在具有变量性质的消亡点集ei∈Δ-，是导致与之相关的基本点集演化的关键，因此，在X上有多少这种变量ei∈Δ-，是关系着X→Y演化的复杂性以及两者差异度的重要因素。例如，经济发达地区，各种各样的建设项目的开工竣工引发的地物变化日新月异。而山区或相对落后的地区，就不及发达地区。地物的演化，首先是与变量ei相关的地物发生演化。

2.3 地物演化的常见类型的数学定义

空集∅是不包含任何元素的集合，空集∅是任何集合的子集，每个集合又都是全集的子集[27]：

∅⊆A⊆X。

(10)

不存在的事物和命题都属于空集的范畴。例如：{x∈R|x2+1=0,R是实数集合}，{地球上高于珠穆朗玛峰的山}，{地球上寿命大于300年的人}，等等。由于(x∩∅)=∅|x≠∅，所以在集合运算中有“抹布”作用，它可以通过与非空集的交运算将其清除。

定义9消亡地物

∃ai∈X∧ai≠∅∈Δ-⟹f1(ai)=∅∈Y|i∈I，

(11)

则称ai为X上的消亡地物。i的标号集为I，表明任何性质的地物都有消亡的可能。

定义10新生地物

∃∅∈X⟹f2(∅)=qk∈Y|qk≠∅，k∈K，

(12)

则称qk为新生地物，它是从空集到非空集的演化。k的标号集为K，表明在任何地方都有某性质k的地物qk新生的可能。

地物的动态演化大体上有宏观上的动态演化和静态演化之分。如果

① ∀t,t′∈ti⟹ai(t′)t⟺消减型演化；

② ∀t,t′∈ti⟹ai(t′)>ai(t)|t′>t⟺增长型演化；

③ ∀t,t′∈ti⟹ai(t′)=ai(t)|t′>t⟺稳定型演化或静态演化。

如在某地建设某一工程qk，工程从开工到竣工期间，属于增长型演化；而被工程qk覆盖的地物(或地物集合)ai便属于消减型演化；重要的历史建筑如北京故宫等，大体上可视为稳定型演化或静态事物。动态和静态具有相对性，比如海底扩张，用现代的测量手段，可测出其扩张速率。在太平洋，单侧的扩张速率达3～8 cm/a，在大西洋和印度洋，是1～2 cm/a。

定义11扩大 满足下列条件的演化：

∃ei∈X∧ei∉A⟹f3(ei)=qA∧A2=f4(A,ei)=(A∪qA)=A2∈Y，

(13)

称A2为A的扩大。

定义12缩小 满足下列条件的演化：

∃ei∈A∈X⟹f5(A,ei)=(A-ei)=A2∈Y，

(14)

称A2为A的缩小[19]。

定义13增补 ∃ei∉X⟹f6:X→Y满足：

Y=f6(X)=(X∪ei)|ei≠∅，

(15)

则称ei为增补元素。地图编绘中增补的新地物即属此列[20]。

定义14舍弃 ∃ei∈X⟹f7:X→Y满足：

Y=f7(X)=(X-ei)|ei≠∅，

(16)

则称ei为舍弃元素。地图编绘中对某些细小元素的舍弃即属此列。

定义15置换 ∃(x,y)∈ai∈X⟹f8:X→Y满足：

Y=f8(X)=(X-ai)∪bk|(x,y)∈bk,i≠k，

(17)

则称bk元素置换了ai元素。

消亡地物和新生地物，本质上是满足特定条件下的置换。

① 当ai≠∅∧bk=∅⟺ai消亡；

② 当ai=∅∧bk≠∅⟺bk新生。

定义16分割 若变换满足：

(18)

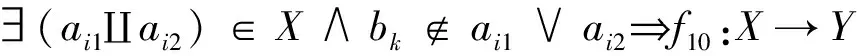
(19)

则称ai为ai1和ai2的合并。合并是由于分割点集bk质变为ai的子集所造成。

分割和合并互为逆变换：

(20)

定义18移位 ∃(x1,y1)∈a,(x2,y2)∈b⟹f11:X→Y满足：

Y=f11(X)=(X-a)∪b，

(21)

∃x1≠x2∨y1≠y2⟺b为a的移位；当且仅当x1=x2∧y1=y2⟺b为a的置换。可见置换是位移值为零的特例[21]。

2.4 从基本点集到目标点集的演化模式

定义19基本点集，结构点集和目标点集。

设A,B,C∈X|ia∈A,ib∈B,ic∈C∧ia≠ib≠ic为X上的基本点集，en≠∅∈Δ-，en消亡的过程同时会使异于en的地物qk的新生，en的消亡和qk的新生过程具有同时性、历时性和渐进性。en称为结构点集。en与基本点集A,B,C∈X在变换f下的运算结果称为目标点集。从属于Y的不同的目标点集的集合A2,B2,C2∈Y便是演化的结果。

定义20地物演化的一般模式。

设A,B,C∈X|ia∈A,ib∈B,ic∈C,ia≠ib≠ic为X上的基本点集，结构点集en=(A∩B∩C)∈Δ-∈X，在en逐渐消亡的过程新地物qk逐渐生成，当en=∅时qk完全生成。其演化模式为

en∈Δ-∈X⟹f(en)=qk∈Δ+,en=∅⟹(A2∪B2∪C2)∪qk=Y，

(22)

式(22)中，i∈I，i的标号集I以及k的标号集K和基本点集A,B,C的目标点集A2,B2,C2的任意性，使任何区域X中的相关地类A,B,C，经地类赋值后通过有限的运算，总能实现到目标点集A2,B2,C2的变换。由于消亡地物en和新生地物qk的边界相同，即b(en)=b(qk)，而b(qk)又与任意闭曲线同胚，即b(qk)≈l，所以可对任意以闭曲线为边界的闭集的消长进行表达。由于存在函数关系：A2=f(A,en),B2=f(B,en),C2=f(C,en)，从而可对Y上的点集的相互关系和状态进行表达。本地物的演化的一般模式对地物从X到Y的演化具有很强的描述和解释功能。图1为地物演化的一般模式。

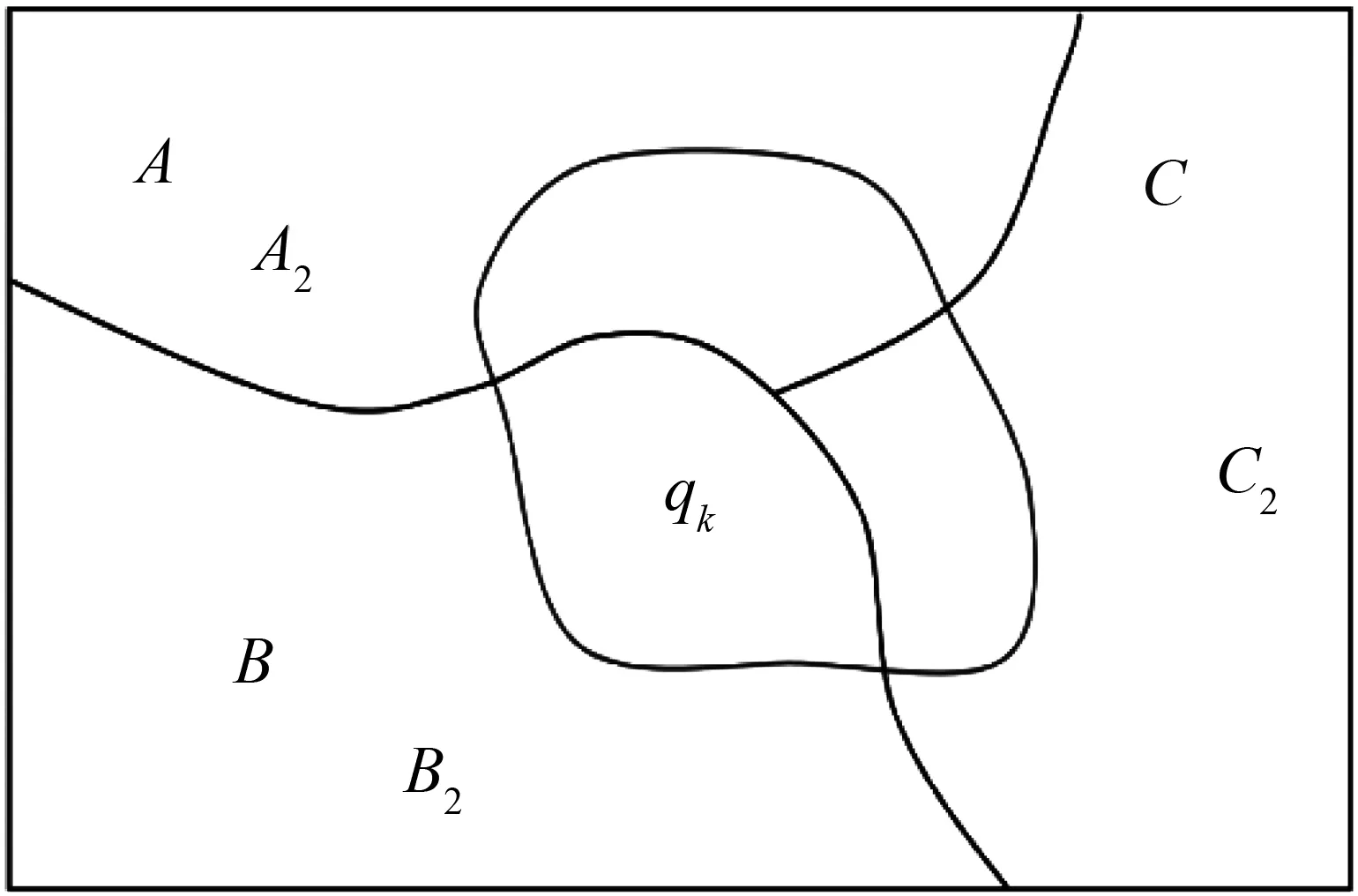
图1 基于结构点集消长的地物演化

例如，qk是一座工厂，那么en就是工厂qk覆盖的地类，即基本集合A,B,C的交集。工厂建成后，交集处的某些地类的性质因为由ia,ib,ic都质变成了qk，原来的基本集合A,B,C因结构点集en的质变而演化为A2,B2,C2并同新生的qk一起成了Y的构成元素。

由于Δ-en+Δ+qk=0的地物演化零和律，使en的减少和等量的qk的增加都会引起相关点集的量变和质变，这种消长代数和为零的关系存在于每一时刻，这就是同时性；而qk对en的替代或覆盖有个过程，就像每一项工程建设都有一定的工期一样，这就是历时性和渐进性。由于那里有演化那里就必需遵循地物演化零和律，而地物演化零和律又必然引起相关地类的量变和质变，从而使地物演化具有必然性，这就是地物演化的内在逻辑。

3 实例

图2中，设t1时刻的区域X的地物类型和结构为

X=A∪B∪C∪D，

(23)

到t2时刻时区域演化为Y，其地物类型和结构为

(24)

从X到Y的各基本点集的演化过程如下。

①en1∈B的消亡并质变为A地类后使A扩大为A2：

∃en1∈B⟹f(en1)=qk1⟹(A∪qk1)=A2∈Y。

(25)

②F2和G2地物的新生：

∃en2∈D⟹f(en2)=qk2=F2∈Y,∃en3∈D⟹f(en3)=qk3=G2∈Y。

(26)

③ 被河流C分隔的公路I2-1和I2-2的生成：

(27)

④ 桥梁H2和C2的生成：

∃en6∈C⟹f(en6)=qk6=H2∈Y∧C2=(C-en6)∈Y。

(28)

(29)

⑥ 演化后B类地物的状态：

(30)

⑦ 演化后D类地物的状态：

(31)

经过上述七步的运算，实现了从基本点集X到目标点集Y的演化。

4 结论

空间和时间是物质固有的存在形式，爱因斯坦的狭义相对论已证明了物质存在与空间和时间的不可分割性。各种不同性质的地物，本质上是不同性质的点集。基于自然原因的自然灾害和按人类的主体意图实现的各种建设，都会使相关区域的不同性质的点集发生变化，从而使地物地貌发生变化。物质存在的充要条件是空间非空性和寿命为非零实值。地物的演化本质上是一种点集性质的变换的问题。某类地物的消亡必然引发另一相关地物的新生，消亡地物和新生地物的代数和恒为零，这就是地物消长零和律，它是地物演化的铁律。地物的消长具有同时性、历时性和渐进性。给出了若干地物演化算子的数学定义。X上的基本点集A,B,C∈X在具有消亡性质的结构点集en的作用下，由于en的消亡与qk的新生而改变了点集的关系和结构，从而演化为A2,B2,C2,qk∈Y的目标点集。通过与基本点集有某种关系的结构点集的消长而导致目标点集的演化实现，解读了地物演化的一般模式。通过实例，阐释了具有某种基本点集的空间关系的X区域演化为目标点集Y的各类地物的演化过程。任何确定的区域，给其点集代数符号赋值后，经过有限的布尔运算，必定演化为目标点集。