园林修剪机械手运动学与动力学仿真分析

沈小滨,唐竞,许恩永，蒙艳玫*,韦锦,王辉,李怡哲

(1.广西大学 机械工程学院，广西 南宁 530004；2.东风柳州汽车有限公司，广西 柳州 545005)

0 引言

目前行业常用绿篱修剪养护工具主要以手持式和燃油式为主[1-2]，不仅功能单一，而且依赖大量人工，耗时费力、污染大，无法满足社会发展要求。张波等[3]设计了一款电动式遥控修剪机，提高了作业人员安全性，但功能单一；戴有华等[4]设计的手推式绿篱修剪机降低了作业强度，然而选用往复式刀具使其并缺少机动性；文献[5-7]提出的车载高速绿篱修剪机，以燃油作为修剪机动力源，对环境污染较大，文献[8-9]将避障算法应用于绿篱修剪上，虽能提高自动化程度，但仍处于理论研究阶段，实用性差。因此，本文从实用、创新角度出发研究设计一款修剪机械手，可满足传统园林常用养护作业要求或应用轨迹规划完成复杂造型修剪。同时借助Simulink仿真平台对修剪机虚拟样机进行运动学和动力学联合仿真[10-11]。

1 修剪机方案设计及运动学建模

1.1 园林修剪机总体方案

根据景观园林实际情况，修剪机械手需完成普通平面的修剪，还需要进行快速的半球、圆柱、圆锥等几何造型修剪，对修剪机的灵活性要求较高，因此以机动性强的多自由度关节型机器人作为解决方案。关节型机器人在农业和林业上多用于采摘或拾取[12-13]，由舵机或者伺服电机驱动，末端执行器为一抓持机构，本文所研究的园林修剪机械手主要基于该类关节型机械手特点进行设计，采用步进电机驱动，末端执行机构为修剪刀具系统，总体方案如图1所示。主要由旋转底盘、底座、大臂、中臂、旋转机构、小臂、刀具系统等组成，具有6个关节，整个系统由6个步进电机和2个刀具电机驱动组成。

图1 园林修剪机三维模型图

修剪机底座控制机械手整体水平方向的转动，大臂、中臂控制机械手俯仰运动，同时伸展时可增加修剪机工作范围，小臂与刀具的运动由旋转机构决定，小臂部分实现对修剪刀具的水平360°旋转，各关节通过减速器与步进电机相连，可实现修剪机在工作空间内的灵活动作；末端执行机构为修剪刀具系统，由刀盘、刀架和刀盘高速电机组成，为增强修剪机实用性与便捷可更换性，刀具部分可选用造型修剪刀具进行一次性成型修剪，或者选用通用刀具进行轨迹规划修剪；修剪机整体通过旋转底座与承载车相连。

1.2 基于改进D-H法搭建修剪机坐标系

由于机器人经典D-H建系法与Solidworks模型中存在描述方式不通用的局限性，本文采用改进D-H法建立机械手的坐标系[14]。参考坐标系0在底座上，在不影响求解结果的前提下，为提高求解速度，需要对末端执行器进行简化处理，即修剪刀具系统部分，将该部分设在修剪机小臂即连杆5的末端。其余连杆坐标系定义在各臂杆关节点处。图2为六自由度园林修剪机的坐标系简图，表1为各连杆参数。

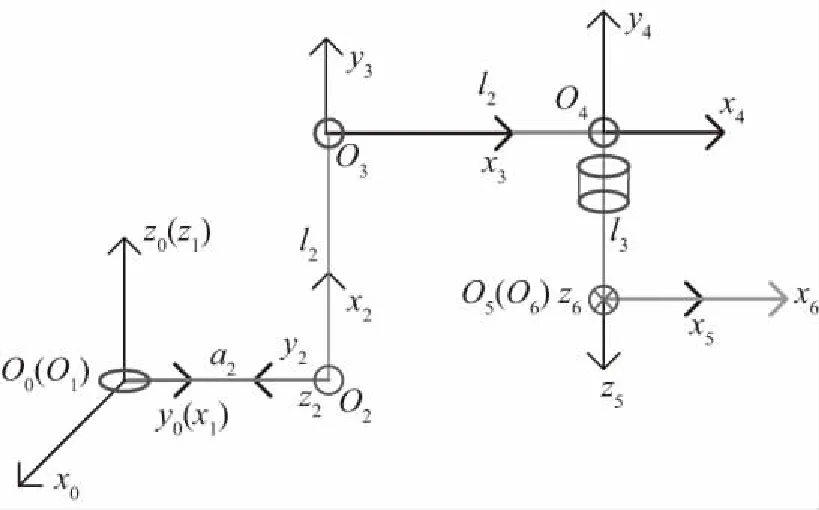
图2 修剪机械手改进D-H坐标系

表1 修剪机连杆参数表

根据上节设计的机械手三维模型，a=135 mm，l1=968 mm，l2=873 mm，l3=390 mm。

1.3 修剪机正运动学分析

根据串联机器人两相邻连杆i、i-1间的齐次变换矩阵[14]推导公式：

(1)

结合修剪机连杆参数，可以得到机械手6个连杆的变换矩阵：

式中，ci=cosθi，si=sinθi，i=1,2，…,6。

则末端执行器相对基坐标的位姿即修剪机刀盘位姿计算式：

(2)

1.4 修剪机逆运动学分析

逆运动学求解即根据修剪机末端执行器即刀盘相对基坐标系位姿，结合连杆参数，求解出修剪机各个对应关节变量的值。根据上节给出的各连杆变换矩阵，可得

(3)

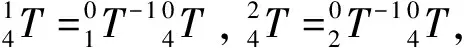
θ1=arctan2(py,px)，

(4)

(5)

θ3=arccos{[(c1py-s1px)2+(c1px+s1py-a)2+pz2-l12-l22]/(2l1l2)}。

(6)

此时，坐标系O4的逆解已经求得，即给出O4位姿，即可得到θ1、θ2、θ3的值并使机械手前三个连杆到达相应位置。结合修剪机实际工作需求，关节θ4、θ5、θ6的逆解与造型轨迹存在约束条件，因此在下一节进行求解。下面求解以O4点为基准的机械手末端姿态，刀盘的旋转点O5与O4位姿关系如图3所示。其中λ4表示连杆5与竖直地面方向在O4关节处的角度变量，刀盘点相对点O4的向量为(Dx,Dy,Dz)。

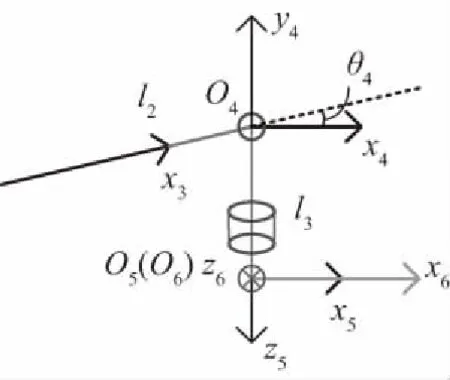
图3 刀盘点的位姿关系

由图3可知，O5相对于O4的向量为

Dx=-l3sinλ4sinθ1，Dy=l3sinλ4cosθ1，Dz=l3cosλ4。

结合修剪机械手的实际情况，需要将连杆5始终保持与地面垂直，即λ4=180°。

因此其向量为-l3，0，0，故O5的机械手位置正解为

5px=4px+Dx；5py=4py+Dy；5pz=4pz+Dz。

(7)

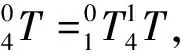
5px=c1(l1c2+l2c2c3-l2s2s3+a)，

(8)

5py=s1(l1c2+l2c2c3-l2s2s3+a)，

(9)

5pz=l1s2+l2s2c3+l2c2s3-l3。

(10)

由于求解时，O5和O6为同一点，O5的位姿函数也即O6的位姿函数。

2 半球造型的轨迹规划

2.1 半球轨迹方程

设半球螺旋线选取的点数为N=100；螺旋圈数C=8，每2π为一圈，球半径为R=25。高度坐标为h；螺旋角度t，设球表面上的圆环半径为r。半球螺旋线轨迹方程参数关系图以及半球螺旋线轨迹方程插补点视图如图4、图5所示。

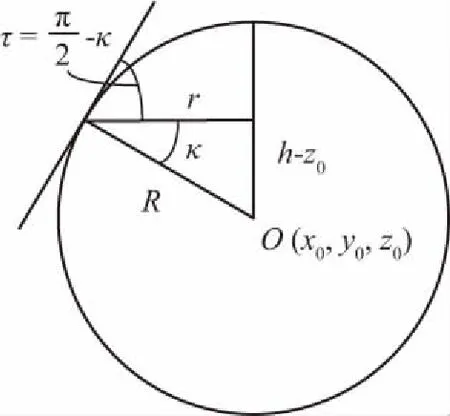
图4 半球螺旋线示意图

图5 半球螺旋线轨迹插补点

2.2 半球点集与关节空间坐标系转换

计算出半球螺旋线点的位置(x，y，z)、旋角集t[i]、切线角集τ[i]等参数后。需要将其转化为机器人关节空间坐标系下的相关值，即转化为修剪机各关节的角度θ1,θ2,θ3,θ4,θ5,θ6变化量。θ1,θ2,θ3是满足D-H坐标系的变量，而使用的θ4,θ5,θ6是由一定约束条件下求取，并不是严格意义上的D-H坐标系上的角度，后三个关节变量是修剪机刀盘位置特性决定的，为避免混淆，求解过程用γ4,γ5,γ6表示。

根据工作时的限制条件：修剪机修剪时，刀具始终与球形绿篱相切，因此允许在γ5未知时，求解出O4的位置。根据工作状况，由图6分析，小臂l3在工作时可能存在竖直和非竖直两种情况，而竖直情况下机构受力更合理，因此下面讨论l3在竖直状态下工作时的求解情况。

图6 刀盘位置的示意图

竖直情况下计算O4的位置，在γ4=0，0≤t<2π的情况下，f为刀盘相对于中臂的距离。

x4=x+fcosτsint，y4=y-fcosτcost，z4=z+l3+fsinτ。

θ1,θ2,θ3根据式(2)(3)(4)求得，据图6：θ1>0，γ5=t-θ1；θ1<0，γ5=2π-[(2π-t)-|θ1|]=t-θ1；即无论在何种情况，γ5=t-θ1，γ6=τ，即γ6=θ6。当γ4=0时，θ4=-θ2-θ3；到此θ1,θ2,θ3,θ4,γ5,γ6已经确定。根据刀盘半球运动点集解出修剪机运动学反解，结果见表2。

表2 修剪机半球轨迹规划各关节参数

3 仿真与试验

3.1 联合仿真环境搭建

① 建立简化的修剪机模型：为减少运算量，提高仿真成功率，将实际机械手模型中一些对整体质量影响很小，基本不会影响仿真结果的零部件进行简化处理。

② 将修剪机模型由Solidworks 2019导入至Simulink 9.7环境中：使用Matlab Simscape插件将机械手的Solidworks模型转化为可以进行Simulink建模的urdf文件[16-17]，同时建立各关节参考坐标系并设置相关约束类型。然后将urdf文件导入Simulink，使用Smimport命令创建slx文件。

③ 在机械手模型基础上搭建联合仿真环境：模型主要包括Motion Actuated和Torque Actuated两部分功能。图7为模型主界面，分为路径点输入、控制决策状态机和机械手执行环境三部分。图8为机械手运动学仿真，主要由正逆运动学模块构成，同时输入驱动力，各关节扭矩由模型仿真而得。图9为机械手动力学仿真，由正逆动力学模块和一个Task space control模型组成，即在笛卡尔坐标空间内，直接控制刀盘的位置，并调用Simulink PID模块去消除刀盘的位置误差。前馈部分计算抵消重力的力矩，反馈部分用PID去控制刀盘的位置，然后用Jacobian矩阵将刀盘的力矩，转化成各个关节的力矩。

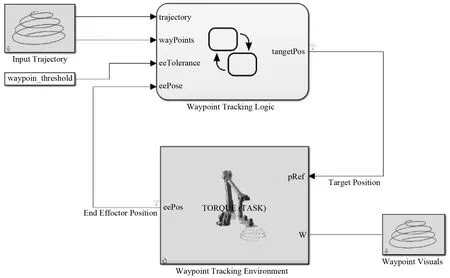
图7 联合仿真环境的搭建

图8 仿真环境的搭建(Motion Actuated)

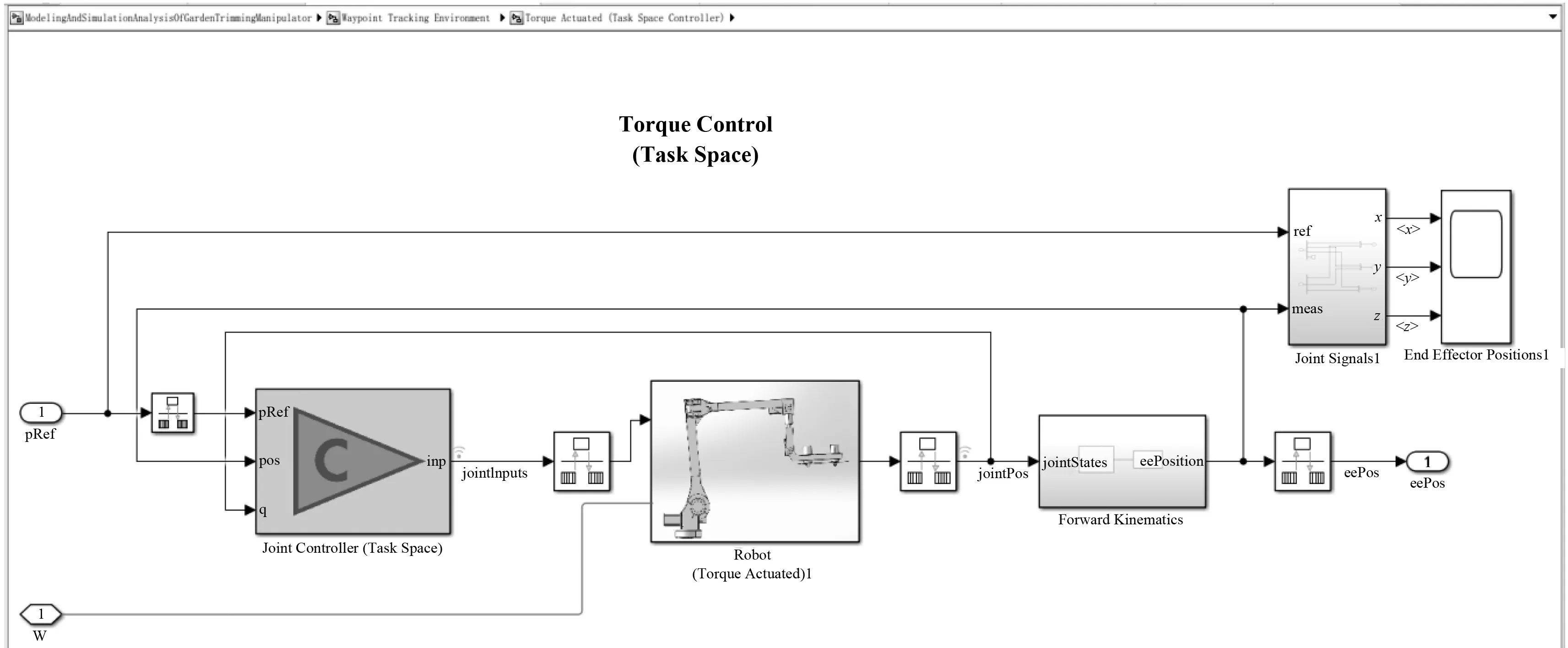
图9 仿真环境的搭建(Torque Actuated)

3.2 仿真结果分析

由仿真过程得到修剪机初始位置时的位姿如图10表示，其中刀盘坐标(0，1.008，0.578)。当修剪机处于初始位置时，θi=[π/2,π/2,-π/2,0,0,0]，由式(2)得

图10 机械手的初始状态

(11)

对比分析可知修剪机械手正运动学的计算求解结果与仿真结果一致，验证了修剪机正运动学的正确性。图11为修剪机械手半球造型仿真过程。其中半球直径为500 mm，仿真步长0.1，仿真时间25 s，仿真时将末端执行器动作轨迹显示出来。可以看出，刀盘运行轨迹为半球形状且轨迹平滑，机械手无突变位姿，表明基于半球螺旋线的轨迹规划造型修剪算法合理性，以及修剪机逆运动学解算的正确性。观察机械手与修剪半球相对大小，确定修剪直径范围选取合理，能在复杂环境下给机械手更多操作空间。

图11 机械手造型修剪

通过运动学仿真，获取修剪机末端速度曲线与位移曲线相关数据如图12和图13所示；可以看出，所设计的园林修剪机械手的末端即刀盘轨迹在各空间坐标方向上的速度及位移变化平滑无突变，表明各臂杆在运动过程中运行平稳、流畅。

图12 末端速度曲线

图13 末端位移曲线

通过动力学仿真，得到修剪机械手各驱动关节部分所需的力矩大小情况如图14至图17所示。图中X、Y、Z分别为相应关节在这三个方向上的分量，三个方向的合力矩用Mag表示。由修剪机各主要关节的扭矩变化图可以看出：大臂、中臂、小臂、刀具系统这四个旋转关节的最大扭矩分别为1 200 N·m、500 N·m、110 N·m、45 N·m。

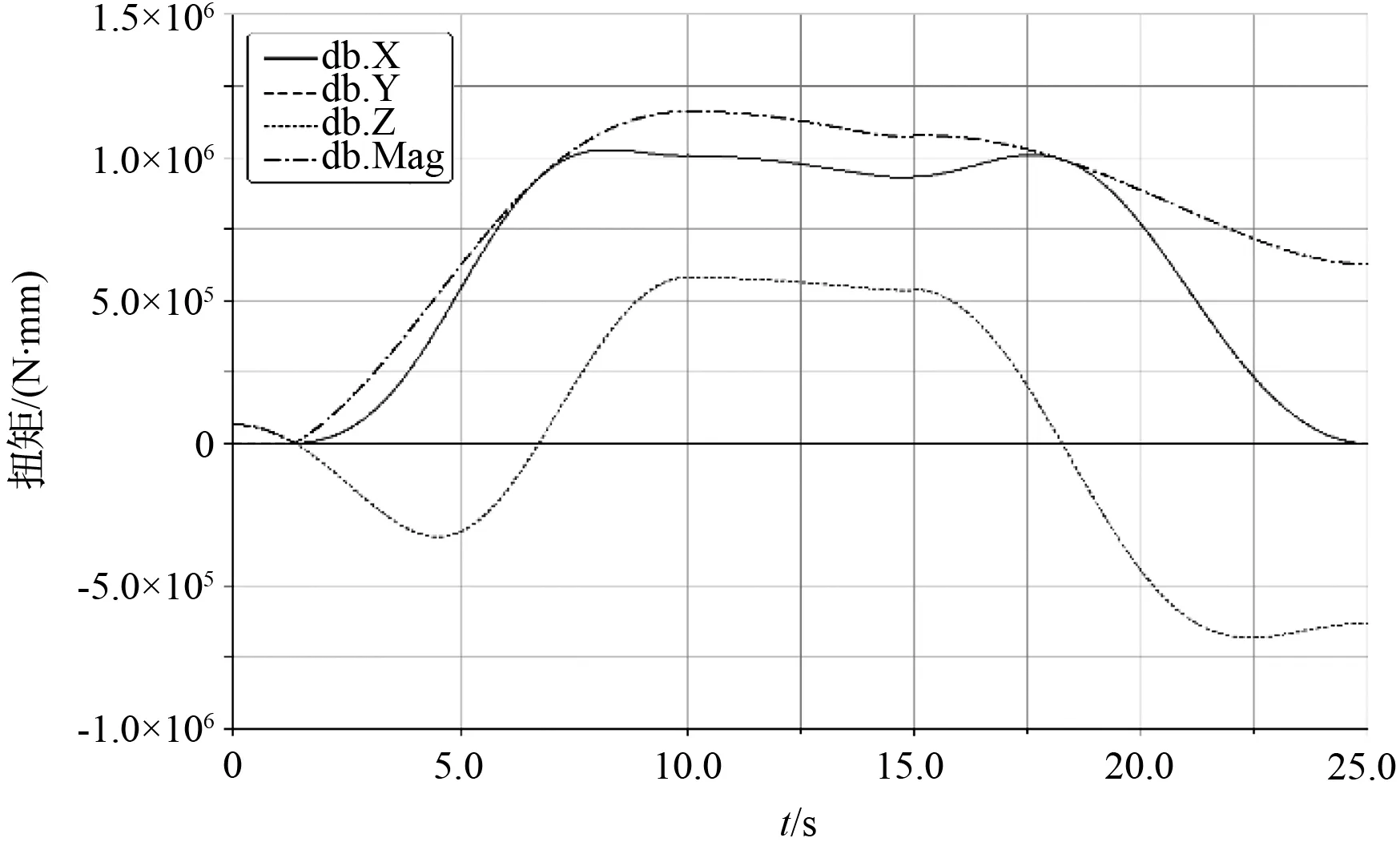
(a)大臂扭矩变化

3.3 试验验证

为验证理论计算的准确性，对所研制的园林修剪机械手各零部件进行选型并完成试验样机制造与装配，如图15所示。

图15 修剪机实验样机

在学校绿化带里选取球型绿篱进行造型修剪，试验过程如图16所示。首先初始化机械手各关节位置，并通过承载车移动机械手本体使小臂位于待养护绿篱的中上方，然后启动刀具系统、控制系统开始造型修剪程序。试验所选取的绿篱直径为400～700 mm，枝条直径为2～7.5 mm，结果显示造型修剪效果良好，平均修剪一株时间为9.5 s，表明机械手运动学方程正确，造型修剪算法合理；修剪机电机运行平稳无过载，动力学建模正确，满足养护工作要求。

(a)修剪前

4 结论

①提出一种多功能园林机械手复杂曲面的造型修剪方法，完成了对园林修剪机械手的正逆运动学的分析和求解以及半球螺旋线的轨迹规划。

② 为了确保修剪机能够完成既定的任务，保证各关节的驱动部分能够输出足够的力和力矩，基于Simulink Dynamics Blocks建立修剪机的动力学模型，确定机械手各关节中速度和力之间的关系，为电机选型提供理论基础。

③ 将园林修剪机械手的虚拟样机在Simulink中进行运动学和动力学建模仿真，不但验证了设计的合理性，也确定了各关节驱动部分保持正常运行情况下所需驱动力的大小。

④ 物理样机试验结果表明修剪机运动学与动力学模型求解正确，半球造型算法合理，养护效率明显提高，控制算法的加入也大大提升了修剪机的自动化程度。

⑤ 本研究不仅为园林机械的下一步无人智能化作业研究打下基础，也对绿化养护设备行业提供一定参考。