基于有限元的辊式制粉磨辊温度场分析及试验验证

胡小青 ,李兴慧

(1.四川工程职业技术学院，四川 德阳 618000；2.四川省冲压发动机先进制造技术工程实验室，四川 德阳 618000)

辊式磨粉机是小麦制粉的主要设备，磨辊是该设备的核心部件[1].小麦制粉过程中，由于物料与磨辊表面的剧烈摩擦，造成辊体温度逐渐升高并持续处于高温状态，有时磨辊表面温度高达60 ℃以上[2-3].磨辊温度过高会造成面粉营养损失、产品质量降低、研磨失效、磨辊寿命降低以及增加电耗等问题[4-5]，因此，降低磨辊温度是保证面粉质量的关键措施之一.科研工作者对于磨辊温度的研究主要包括两个方面，一是降温冷却的方法，设计了水冷却式磨辊、风冷却式磨辊和热管冷却式磨辊，并在实践应用中检验制粉效果[6-7]；二是分析磨辊热源并计算小麦制粉过程中产生的热量，进而研究操作参数和结构参数对磨辊温度变化的影响规律[8-10].然而，关于磨辊内部温度场分布的研究鲜有文献报道.

本研究在调研小麦制粉的实际工况的基础上，建立合理的磨辊瞬态温度场数值模型，利用有限元软件ANSYS进行求解分析，并结合现场的实测数据，验证数值模型和模拟结果的可靠性，以期为磨辊的设计和优化及磨辊温度降低提供参考依据.

1 数值模型的建立

磨辊的结构示意图如图1所示.

图1 磨辊结构示意图

1.1 几何模型的建立

为更准确实现磨辊温度场的数值模拟，对几何模型作出如下假设：(1)磨辊材料均匀且沿中心轴对称；(2)忽略磨辊上较小的孔、倒角以及辊轴与辊套连接位置的影响，去掉磨辊轴端部分[11]；(3)磨辊温度场属于三维瞬态问题，考虑到磨辊几何形状为轴对称实体，工作过程中边界条件呈周期性变换，磨辊的任一子午面在任一周期中经历和表现的热行为是一致的，只是时间先后上的差别，磨辊某一瞬态的热行为可以近似描述为磨辊中某一子午面在一个周期内热行为的时间积累[12]，这样，将磨辊的三维瞬态温度场简化为磨辊任一子午面的二维轴对称温度场的时间积累[13-14].简化后的模型如图2所示.

图2 磨辊二维模型简化图

1.2 边界条件及对流换热系数

针对制粉中复杂多变的边界条件，根据制粉生产中的实际工况，对简化后的磨辊二维模型边界作如下规定：图2中1处辊轴与轴承摩擦热视为稳定热流边界[15]；图2中2处磨辊两端与空气的接触为空气受迫对流换热；图2中3处辊体表面根据磨辊与物料摩擦产生的热流施加热流载荷，同时磨辊转动时，其表面换热属于空气受迫对流换热，认为沿轴向、周向空气运动规律相同，从而磨辊表面与空气的对流换热系数相同；磨辊轴端作绝热处理.

则磨辊热边界条件为：

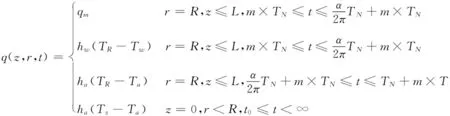
(1)

式中：qm为传入到辊体的摩擦热；m为周期数；TN为磨辊转动周期；L、R、z分别为磨辊辊长、半径、轴向坐标；hw为磨辊表面与物料之间的换热系数；ha为空气对流换热系数；TR、TW、Ta、Tz分别为磨辊表面、物料、环境温度、磨辊端面温度.

将磨辊表面空气的对流换热视为平面散热[16]，根据平面散热理论，磨辊表面空气对流换热系数为：

(2)

式中：λa为空气导热系数；γ为空气的运动粘度；L为壁面长度；μa为相对空气流动速度.忽略周围温度变化的影响，则γ、Pr和λα为定值，ha只与磨辊表面线速度相关.

2 结果与分析

2.1 磨辊温度场计算结果及分析

利用ANSYS前处理模块结合图1尺寸建立磨辊模型；磨辊主要由3种不同材料构成，其中外层为白口铁，内层为灰口铁，辊轴为45钢[17]，3种材料属性如表1所示，根据表1数据定义模型材料属性.本研究采用的热分析单元为四边形的PLANE55单元[18]，并设置单元属性为轴对称，采用映射网格划分方式，划分结果如图3所示.

图3 网格划分

表1 材料属性参数

对表2磨粉机操作参数下的磨辊不同边界施加边界载荷，设置初始温度为25 ℃.在磨辊表面创建表面效应单元SURF151，并将热流载荷施加于表面效应单元上，将对流载荷施加于平面热分析单元节点上[19]，在求解选项中定义分析类型为瞬态分析，温度偏移量为273，模拟时间10 800 s，步长为15 s，求解分析，获得不同时刻温度场云图如图4所示，辊体不同位置温度随时间变化曲线图如图5所示，图6所示为辊体轴表面温度曲线图，图7所示为辊体温度场三维拓展图，图8所示为辊体不同位置热通量随时间变化曲线图.

表2 磨粉机操作参数

由图4可知，随着制粉时间的推移，辊体温度不断升高，辊体表面温度最高，辊轴两端温度最低.这是由于制粉过程中，磨辊表面与物料剧烈摩擦，机械能转化成热能并传入辊体，且由辊体中部向辊体两端、辊体内部迅速扩散，导致辊体温度不断升高，并且长期处于高温状态.

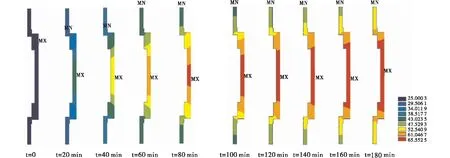
图4 不同时刻温度场云图

图5中显示，在制粉开始的一段时间里，辊体表面温度由25 ℃迅速升高至60 ℃以上；在随后的时间里，温度上升速率逐渐减小，上升幅度明显减小，直至稳定在65.6 ℃左右的高温状态；辊体两端和内部温度的变化规律与辊体表面趋于一致，但上升速率和上升幅度都不及表面高，最终也趋于稳定状态.这是由于在制粉开始的一段时间里，辊体与环境的温度差较小，根据对流换热理论可知，当换热系数一定时，对流换热的热量总值与两物体间的温度差相关，相同时间里，温度差越大，换热速率越快，换热量也越多[20].因此随着制粉时间的增长，辊体表面与环境的温度差不断增大，辊体向外散发热量的速率也越来越快，直至传入辊体的热量与散发的热量相等，最终达到动态平衡，辊体温度场趋于稳定状态.

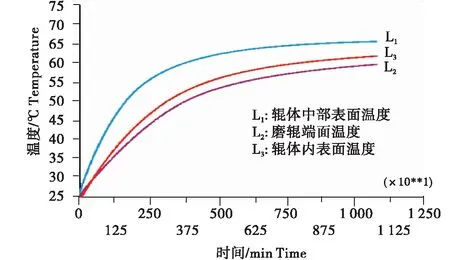
图5 辊体不同位置温度随时间变化曲线图

由图6可以看出，辊体表面温度沿着辊体一端至另一端呈现中间高两端低的分布，两端较中间温度最大差值为5.5 ℃.这是由于辊体表面的热量传入辊体后向辊体两端扩散；辊体高速转动时，在辊体端面位置空气与辊体的对流换热可看作是受迫对流换热，热量不断从辊体两端流出，使得辊体温度趋于稳定时，辊体两端温度较中间低.

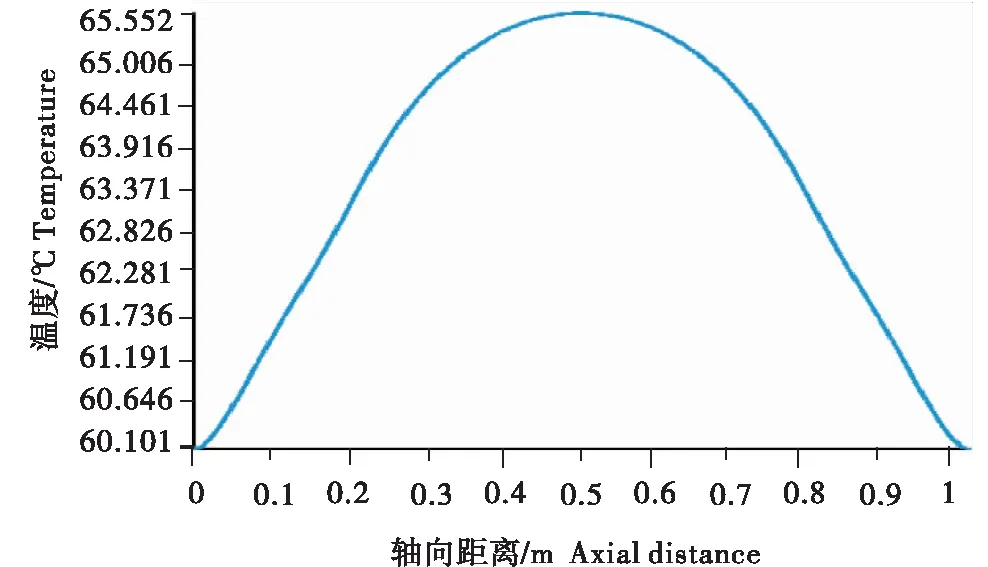
图6 辊体轴表面温度曲线图

从图7辊体温度场3/4拓展图可以直观清晰地了解整个辊体温度场的分布状况，由于辊腔为一密闭的空间，辊体内部的热量不能很好地向外扩散，这也是导致普通磨辊温度过高的原因之一.

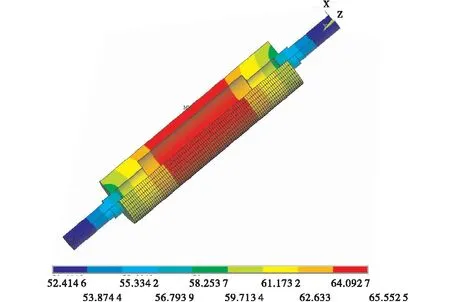
图7 辊体温度场三维拓展图

图8显示制粉开始时，摩擦热传入辊体，辊体表面及辊轴热通量达到最大，随着辊体温度的升高，辊体表面热通量逐渐减小直至趋于稳定状态；4 245～7 500 s这一阶段里，辊体热量传入辊轴，导致此阶段里的辊轴热通量出现回升，随后逐渐减小.随着传入到辊体的热量逐渐减少，在制粉3 225 s后，辊体端面热通量逐渐减小.

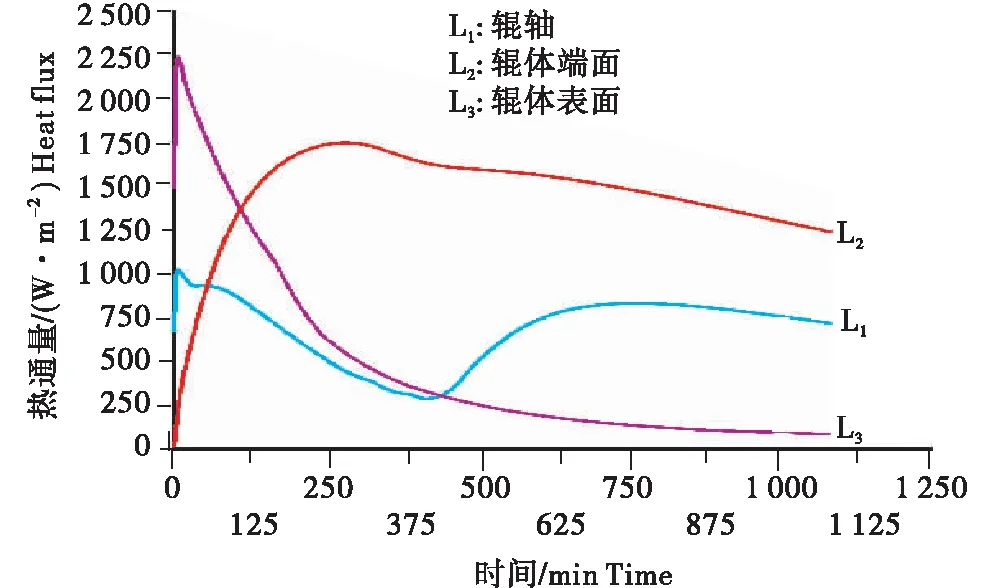
图8 辊体不同位置热通量随时间变化曲线图

2.2 转速对磨辊温度场的影响

制粉时提高磨辊转速，研磨速度加快，生产效率提高，但磨辊转速的快慢是导致辊体温度高低的主要原因之一[21].为研究磨辊不同转速与辊体温度场之间关系，选用制粉中快辊常用转速450、550、650 r/min为参数项，在ANSYS中设置旋转件模型相应转速，对在同等条件下的磨辊瞬态温度场进行模拟研究，结果如图9所示.

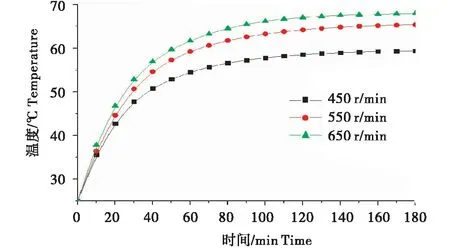
图9 不同转速下磨辊表面温度随时间变化曲线图

由图9可以看出，不同转速下的磨辊表面温度上升规律趋于一致；对比3条曲线可以看出，在工作初始阶段(0～60 min)转速越高时，磨辊温度上升越快，上升幅度越大；但随着快辊转速的增加，辊体表面温度由室温上升至稳态所需时间更长，磨辊表面温度的增幅相对减小.

绘制不同转速下磨辊t=10 800 s时的温度场云图如图10所示，图10显示，3种不同转速下磨辊最终温度场分布规律基本一致，但温度值大小有所区别；转速为450、550、650 r/min下磨辊稳定运行时，最高温度分别为59.45、65.55和67.98 ℃；这是由于在轧距、速比、喂入量不变的情况下，随着两辊转速的提高，使进入研磨区的物料料层变薄，工作辊与更多颗粒发生摩擦，产热量增加，但同时磨辊与空气的接触频率增加，散热加快，因此出现转速增加，温度相对增幅减小的现象.

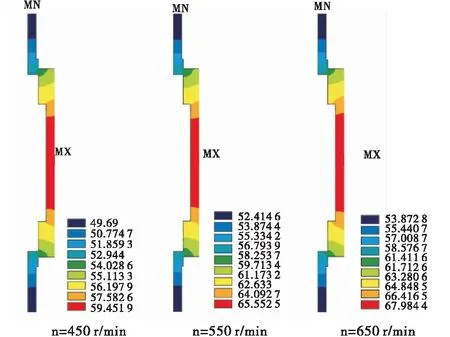
图10 不同转速下磨辊温度场分布云图

3 验证试验

为进一步验证磨辊温度场数值模型及仿真结果，对表2操作参数下磨辊工作过程进行温度测定试验(环境温度为25.3 ℃).试验基于MDDK型磨粉机，考虑到磨辊制粉过程中处于旋转状态接触式温度计无法直接测量磨辊表面温度，选用红外线测温仪进行测温，在磨辊的轴向对应机壳上等距布置7个测温点.测温场景如图11所示，每隔10 min测量每点温度，最终绘制不同时刻辊体表面平均温度值与计算值曲线如图12所示.

图11 温度测定试验场景

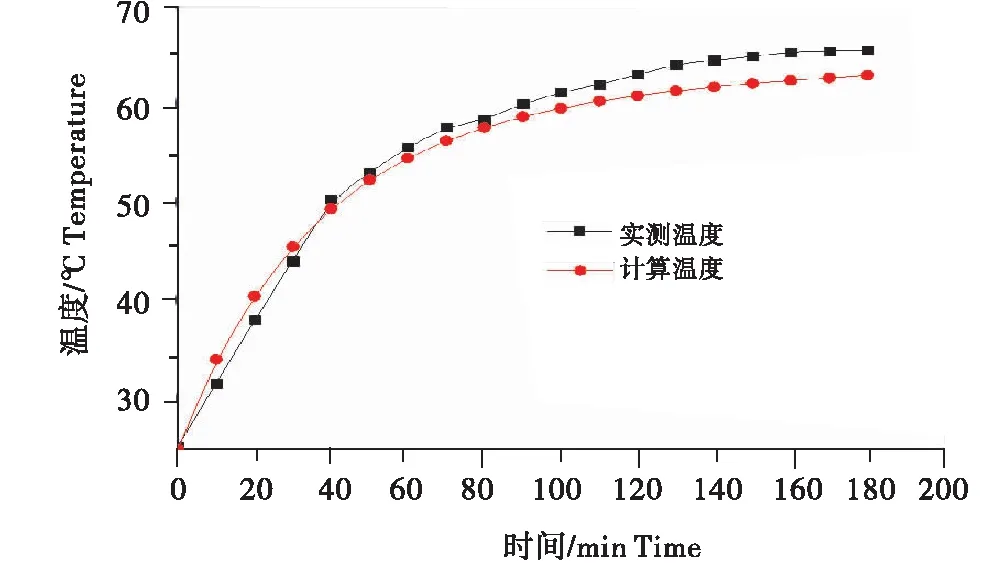
图12 计算平均值和实测平均值曲线对照

从图12曲线可知，两条曲线温度上升的趋势基本趋于一致；实测值与计算值基本吻合，最大误差为2.97 ℃.计算值与试验值产生偏差的主要原因有：①在制粉开始的一段时间里，磨粉机还未达到稳定运行状态，造成计算值略高于实测温度值；②环境温度随着制粉时间不断升高，导致散热效果降低，实测温度值高于计算值；③有限元计算过程中的数值误差等.综合上述因素，虽然仿真值与试验值存在一定偏差，但预测精度对于实际应用是可以接受的，验证了磨辊温度场数值模型和仿真结果的可靠性.

4 结论

在制粉开始阶段，辊体表面温度由25 ℃迅速升高至60 ℃左右；然后温度上升速率逐渐减小，直至稳定在65.6 ℃左右的高温状态.

辊体表面温度沿着辊体一端至另一端呈现中间高两端低的分布；不同转速下磨辊表面温度上升规律基本一致，转速越高时，磨辊温度上升越快，上升幅度越大.

试验测量辊体表面平均温度值与有限元计算值基本吻合，最大误差为2.97 ℃，温度上升趋势基本一致，验证了磨辊温度场数值模型和仿真结果的可靠性.