考虑风电接入不确定性风险下的电网安全经济协调规划

严太山，熊泽群，郑晓琼，汪太平，吕雪峰，刘 鑫，储贻道

(国网安徽电力有限公司检修分公司,安徽 合肥 230000)

0 引言

2020年国网公司发布“碳达峰、碳中和”行动方案，在双碳目标背景下，清洁低碳的风电等新能源发电将会迅速发展。2020年，中国风电新增装机容量达7 167万千瓦，据风电市场规模预测，预计2060年国内风电装机总容量将达到20.07亿千瓦，风电年发电量约3.85万亿千瓦时。随着风电的大规模开发利用，风电出力的不确定性具有间歇性和波动性两个方面，给系统安全稳定运行带来更多挑战。研究考虑风电接入电网下安全性与经济性的协调规划，对风电的安全有效消纳及评估风电价值方面具有重大作用。

电网的安全性与经济性是电网规划、运行需要考虑的两个重要指标。目前，国内外针对电网安全性和经济性协调方面的研究工作相对较少。文献[2]提出了简易专家系统应用于考虑输电线路的安全性，解决输电线路重载、过载问题，其研究仅为调度快速决策提供依据，且对于经济性的考虑相对较少。文献[3]采用多目标规划与模糊协调技术，以经济性为首要优化目标，发电机组运行限制作为次要优化目标求解发电规划优化问题。文献[4]将电网的经济性与可靠性方面的目标通过线性加权的方法将两者相结合，以协同考虑系统的建设投资成本与切负荷成本为目标建立模型。文献[5]引入电网运行均衡度来衡量系统安全性水平，协同考虑经济指标和安全指标建立双目标优化模型，实现对安全、经济两个方面的协调量化分析。文献[6]运用线性多目标法，以系统发电成本最小和有功静态安全最大作为双重优化目标，进行系统有功调度中的经济性与安全性的分析，实现有功运行点和静态安全域的权衡。文献[7]引入缺电成本，运用电网规划的成本-效益分析法，以供电总成本最小作为目标函数并建立规划模型，将规划方案的可靠性与效益统一于经济性层面。文献[8]针对未来电网的不确定因素所带来的过负荷风险，建立了多目标动态电网规划期望值模型，从风险的角度进行电网规划与决策。上述研究中，规划方案的比选原则，主要考虑的是规划设计中的经济性问题，而安全性方面仅作为约束条件加入到规划模型，或者将安全性折合到经济量纲下追求总成本最小，但实际中对电网安全性损失并未有明确定义，另外，这种对安全性的处理方法也忽视了预想事故发生的频率及可能性，不适用于风电接入电网下的安全性和经济性的综合考虑。

文章通过将风险规划理论应用于电网规划中，既可对电网运行中存在的多种不确定因素进行合理评估，并通过构建相关的风险性指标来衡量系统运行中的风险，将运行中可能存在风险保持在可以接受的合理区间范围内；另一方面，以衡量电网运行安全性水平的风险指标作为决策的重要依据，在电网规划中充分考虑系统出现故障的可能性及事故后果的严重程度。基于此，文章通过引入概率可用传输容量(Available Transfer Capability，ATC)，在规划阶段综合协调安全性和经济性两方面，实现综合最优规划。

1 风电接入下的风险

当风电接入电网后，由于风电出力的间歇性和波动性，系统的风险度会有所提高。当风电出力出现较大范围的波动，甚至出现大风等极端恶劣的自然天气时，由于系统装机中的风电占比较大，带来功率不平衡量增加，若系统没有配置足够的备用容量，就会导致电网频率出现较大波动的现象。实际中，风电出力的波动程度比电力负荷大得多，且风速受到地理位置和环境等因素的影响，使得风电出力很难预测和控制。因而，对于风电渗透比例较大的电力系统，风电出力的波动特性是引起电网风险的主要原因。

随着接入电力系统的风电场规模越来越大，其出力的波动性、间歇性对电力系统的影响愈加明显，高度不确定的风电场出力等因素将给电力系统规划方案带来安全风险。安全风险主要体现在输电线路过负荷和可用输电能力等方面，表征了输电网安全性。风电出力等不确定因素的存在，使得电力系统潮流具有不确定性，不确定的线路潮流将导致线路有一定的概率出现过负荷以及输电系统具有不确定的可用输电能力。为了衡量不确定条件下线路潮流过负荷情况，提出了潮流越限概率、失负荷概率以及电量不足期望值等指标；为了衡量不确定条件下输电网的可用输电能力，相应地提出了概率可用传输容量指标。

2 风电接入不确定风险下电网规划模型

风电接入给电网带来影响的主要原因在于风电出力具有间歇性和波动性。随着风电场规模的扩大和系统风电装机比例的逐步提高，在系统规划阶段考虑风电场出力的波动性较大时，对于电网线路及输电容量配置来说，若要求电网输电线路在各种不同情况下均不会出现过负荷现象，就需要线路有足够的容量裕度，在实际电网建设中这可能会引起输电容量过度配置的问题，由于投资过高对输电线路运行效益产生负面影响。另一方面，在输电线路规划阶段，出于安全性角度考虑，又要保证留有已一定的输电容量空间，以应对风电等新能源发电出力间歇性等因素。考虑到以上方面，本文分别以输电投资成本和线路概率可用传输容量为目标，建立规划模型如下：

f

:max

R

=

E

=

e

d

(1)

(2)

式中

d

为负荷增长向量；

R

为系统规划方案所对应的输电线路可用传输容量期望值；

N

为电网中的网架线路集合；

c

表示支路新建单回输电线路的投资费用；

z

表示支路

l

的新建输电线路数目。对两个目标函数

f

和

f

采取合并处理，将目标函数转变为一定电网投资成本所带来安全性水平的提升度。规划模型建立如下:max(

f

/f

)

(3)

SP

=

P

+

P

-

P

-

d

(4)

(5)

Z

≤

Z

(6)

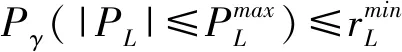
(7)

3 改进小生境遗传算法

遗传算法具有快速随机的全局搜索能力，程序实现相对简单，近年来在电力系统规划、经济调度等领域取得广泛应用。本文所采用的改进小生境遗传算法(Improved Niche Genetic Algorithm，INGA)，在传统算法基础上引入小生境淘汰运算操作，从而更好保持子代样本的差异性，具有很好的全局寻优能力和收敛速度。小生境淘汰操作通过两两比较种群个体样本间的海明距离来实现，海明距离定义如下:

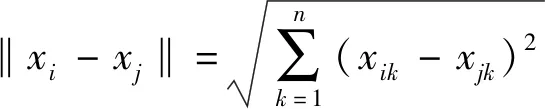
(8)

当‖

x

-

x

‖<

L

时，将会对种群中适应度值小的个体施加惩罚函数。其中，

L

为每次迭代产生不同个体之间距离的判别标准。考虑到进化后期种群个体间的海明距离将会减小，寻优搜索容易得到不需要的局部最优解。因而将

L

描述为种群(个体数为

N

)个体之间海明距离平均值和迭代次数

M

′的动态函数，定义如下:

(9)

算法迭代时，交叉机制中采用式(11)所示的自适应交叉概率，在迭代初期交叉概率较高；迭代后期交叉概率较小。

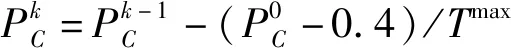
(10)

在迭代后期，保留下来的个体适应度均较高，个体间差异小，群体多样性减弱，此时较高变异概率能更好维持群体多样性，有利于搜索全局最优解。因此，在变异运算中，也采用自适应变异概率，计算方法如下:

(11)

式中

P

表示变异率，

P

1,

P

2分别设置固定变异值0

.

1和0

.

001；

f

代表最大适应度，

f

代表平均适应度；

η

表示最大迭代次数。

另外，为保证每次迭代中最优个体被保留至下一代使得算法能收敛到全局最优解，本文在小生境遗传算法中增加精英保留策略，其原理是把种群在迭代过程中产生的最优个体不采取交叉，而直接被保留至下一次迭代过程。

4 IEEE RTS79算例分析

系统总装机容量为10 215 MW，年最大负荷为8 550 MW，网架如图1所示。遗传算法最大迭代次数为1 000。

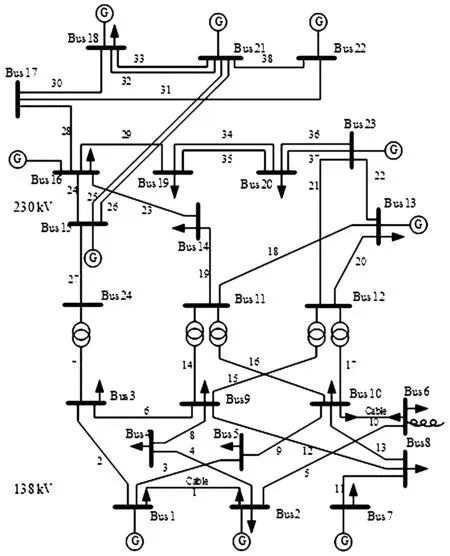
图1 IEEE RTS79系统网架图

设定系统节点23处连接有装机容量为800 MW的两个相同的风电场，假设两个风电场的风机特性相同，并且切入风速、切出风速以及额定风速分别设置为5 m/s，22 m/s，10 m/s；威布尔分布中的尺度参数和形状参数分别取值为6.5和3，风电场的相关系数为0.7。

对所建规划模型运用改进小生境遗传算法求解，获得三个较优的规划方案，如表1所示。

表1 IEEE RTS79系统规划方案

不同方案的对比见表2。由表2所得的三个规划方案的指标可看出，与方案1相比，方案2的输电投资成本比方案1高出2.81%，但方案2的可用传输容量期望值仅较方案1高出2.18%，方案2的高投资并没有带来期望的安全性水平，因而方案1的目标值高于方案2。方案3的输电投资成本较方案1降低了3.39%，然而该方案的可用传输容量期望值较方案1降低4.17%，因而方案3的目标值低于方案1。综上分析，方案1的目标值最大，综合效益最佳，是上述三个方案中的最优方案。

表2 不同规划方案对比

为了进一步分析风电场的接入方式对输电系统的影响，将其中的一个风电场接到节点18，另一个风电场接到节点23，重新规划并利用改进小生境遗传算法求解，获得规划方案4，与方案1比较如表3、表4所示。

表3 不同风电场接入方式的规划方案

表4 不同风电场接入方式的规划方案对比

与方案1相比，方案4的投资成本相比方案1降低5.29%，方案4的可用传输容量期望值相比方案1增加1.98%。可见，方案4输电投资成本较方案1更少，而目标值却高于方案1。方案4应对风电扩建不确定性的效果更好，由于在节点18和23上分别接入风电，带来系统的输电投资成本的下降，同时也增加了概率可用传输容量期望值，使投资效益得以提高。可见，在考虑经济性和安全性的电网协调规划时，风电扩建不确定性对规划方案和电网投资效益均有重大影响。

5 结束语

本文通过分析风电接入给电网带来影响，建立了考虑风电接入风险下的电网安全经济协调规划模型，分析风电扩建的不确定性对规划方案目标值的影响，得到以下结论：

1)最优规划方案实现了投资成本和线路概率可用传输容量之间的协调，达到综合效益的最大化。过多地注重增加投资可使线路可用传输容量略微增加，但造成输电容量的过度配置，并非最优方案。

2)ATC期望值大的规划方案能更好的适应风电扩建的不确定性风险因素，在较低投资成本下能获得较好的投资效益。