三峡库区柑橘土壤水分动态变化的自回归积分滑动平均模型构建

张明博 朱士江 徐文 张涛 刘彩虹 彭玉强 王斌 李虎 王浩 贵树彪

摘要 采用时间序列分析法，针对三峡库区柑橘树根区60 cm深土壤水分建立ARIMA（1，1，1）模型。结果表明，拟合区与预测区相对误差分别为0.37%～7.67%、2.83%～5.56%，平均相对误差分别为4.33%、4.52%，均小于5%。该模型可以很好地模拟与预测柑橘树根区土壤水分的变化趋势，可以进一步应用在其他作物根区的土壤水分监测，为农作物优质生长、节水灌溉提供技术支撑。

关键词 ARIMA模型;构建;时间序列分析;柑橘;土壤水分;动态变化;三峡库区

中图分类号 S152.7  文献标识码 A  文章编号 0517-6611（2021）11-0001-04

doi：10.3969/j.issn.0517-6611.2021.11.001

开放科学（资源服务）标识码（OSID）：

Construction of an Autoregressive Integral Moving Average Model for the Dynamic Changes of Citrus Soil Moisture in the Three Gorges Reservoir Area

ZHANG Ming-bo1，2，ZHU Shi-jiang1，2，3，XU Wen1，2 et al

（1.College of Water Resources and Environment， Three Gorges University， Yichang，Hubei 443002;2.Engineering Research Center of the Ministry of Education for the Ecological Environment of the Three Gorges Reservoir Area， Yichang，Hubei 443000;3. Key Laboratory of Efficient Utilization of Agricultural Water Resources， Ministry of Agriculture， Harbin，Heilongjiang 150000）

Abstract The time series analysis method was used to establish the ARIMA （1，1，1） model for 60 cm deep soil moisture in the citrus tree root area of the Three Gorges Reservoir area. The results showed that the relative error of the fitted area and the predicted area was 0.37%-7.67%， 2.83%-5.56%， respectively， the average relative errors was 4.33% and 4.52%， respectively， which were all less than 5%. The model could preferably simulate and predict the change trend of soil moisture in the root zone of citrus trees， and could be further applied to the monitoring of soil moisture in the root zone of other crops， providing technical support for high-quality crop growth and water-saving irrigation.

Key words ARIMA model;Construction;Time series analysis;Citrus;Soil moisture;Dynamic change;Three Gorges Reservoir Area

土壤水分作为影响作物优质生长的重要因素，受不同地区气候、土壤、灌溉等的影响，存在较大差异性。同时作物的产量与品质作为土壤水分差异性的体现形式，因此对土壤水分预报模型的研究持续被国内外学者广泛关注，并取得了大量成果。土壤水分预报模型可以分为确定性模型和随机性模型两大类[1]，其中确定性模型包括水量平衡模型[2-3]、土壤-植物-大气连续体（SPAC）水分传输模型[4-5]、SPAC水热耦合传输模型[6-7]等，随机性模型包括数理统计模型（包括回归模型[8]、时间序列模型、人工神经网络模型[9-11]等）、随机水量平衡模型和随机土壤水动力学模型[12]等。其中一些精确度较高的模型，对于模型参数的要求存在一定門槛，该研究选取ARIMA时间序列模型对土壤水分进行研究，该模型对数据要求单一，只需要变量自身的历史数据，适用性较强[13]。一些学者通过时间序列分析法对土壤水分进行动态模拟，并取得了一定成效，如康绍忠[14]通过对北方气候条件下的土壤水分模拟得出土壤水分的变化序列满足时间序列的通用加法模型且预测精度较高;刘洪斌等[15]采用AR模型对三峡库区紫色土丘陵旱坡地土壤水分动态进行了模拟和预测;

杨绍辉等[16-17]先后采用ARIMA模型分别对北京市、贵州省土壤墒情进行预测，均对当地土壤墒情及旱情评测提供重要依据;周刘宗等[18]利用时间序列理论分析了降水和土壤含水量的相关关系，认为降水序列为不相关序列，而土壤含水量序列为自相关序列;白冬妹等[19-20]分别采用ARIMA模型对黄土高原柠条林地和淮北平原冬小麦土壤水分进行预测，预测结果均较好。

对柑橘而言，柑橘作为深根系作物，研究深层土壤水分更具有实践意义，因此该研究对60 cm土壤水分变化趋势进行模拟和预测，采用宜昌市夷陵区仓屋榜试验站2019年柑橘生育期土壤水分实测资料，基于ARIMA模型对三峡库区气候下的土壤水分进行模拟和预测，为三峡库区柑橘优质生长提供科学指导，也为节水灌溉、抗旱救灾及农业评估提供一定理论依据。

1 资料与方法

1.1 试验区概况

宜昌市夷陵区仓屋榜试验站位于三峡库区东部，地处111°35′E、30°45′N，海拔112 m，试验区为丘陵旱坡地，坡度为0～20°，20、40、60 cm埋深的土壤水分变异系数分别为28.73%、23.23%、19.60%，土壤类型为棕壤土，柑橘品种为蜜橘。三峡库区属亚热带大陆性季风气候，具有早春、夏热、冬暖、多雨等特点，是全国柑橘优势产业区，但降雨量时空分布不均，存在夏旱连伏旱现象，因此监测和预报土壤水分是预防旱灾、调控土壤水分与柑橘优质生长关系的基础。

1.2 数据采集

2019年5月19日—12月22日，每7 d对样点柑橘树根区60 cm深土壤取样，通过105 ℃烘干法测量土壤含水率。该研究主要针对柑橘树根区60 cm深土壤水分进行分析，并建立ARIMA模型。

为消除坡位差异的影响[21]以及更准确地获取试验区60 cm深度下土壤水分资料，对试验区148棵柑橘树，共选取29棵作为样点树，样点树选取均匀分布在上、中、下坡，所有样点树皆为健康的柑橘树。

1.3 模型简介

ARIMA模型全称为自回归积分滑动平均模型（autoregressive integrated moving average model），可以细分为AR模型、MA模型、ARMA和SARIMA模型，ARIMA（p，d，q）模型是经过d阶差分达到平稳序列要求的ARMA（p，q）模型。模型公式如下：

xt=c+pi=1φ1xt-1+εt-θ1εt-1-…-θqεt-q（1）

式中，xt为零均值平稳序列;c为常数;p 为自回归阶数;q为滑动平均阶数;φ1，φ2，φ3，…，φq为自回归系数;θ1，θ2，θ3，…，θq为滑动平均系数;εt为零均值，方差为σ2ε 的平稳白噪声。

1.4 数据处理

1.4.1 数据处理工具。

运用Matlab和Excel软件对数据进行处理与建模分析。

1.4.2 数据标准化。

为提高运算精度，需对原始数据进行处理，数据处理的常用方法有规范化处理、正规化处理（即z-score标准化）、归一化处理和取对数处理等。该研究采用正规化处理：

Yt=Xt-uσ（2）

式中，Yt 为标准化变量;Xt 为原始变量;u为{Xt}的均值;σ 为{Xt}的标准差。

1.5 时间序列平稳性检验

ARIMA要求时间序列数据需满足平稳性检验，即均值不随时间变化而改变，自相关系数只与时间间隔相关。对大部分时间序列而言，存在明显的波动性和趋势性，需对不平稳时间序列进行差分处理以满足序列平稳。差分公式如下：

ΔYt=Yt-Yt-1（3）

式中，ΔYt为一阶差分后的标准化变量。

2 模型建立与模式預测

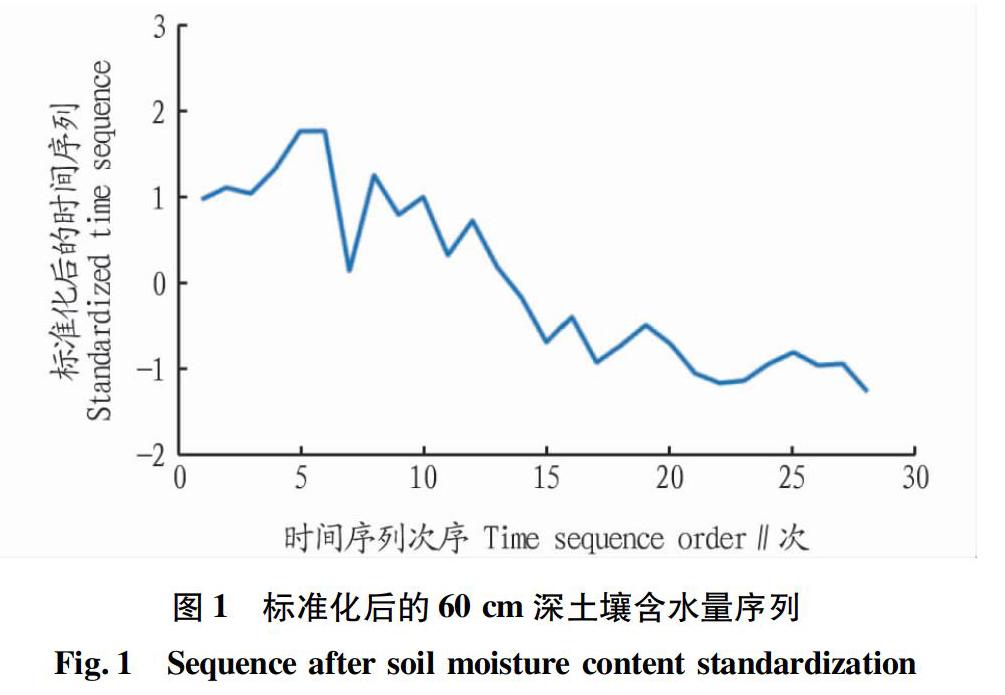
2.1 数据标准化 对原始数据进行标准化处理，得出标准化处理后的60 cm深土壤含水量序列如图1所示。

2.2 时间序列平衡性检验

由图1可知，60 cm深度土壤含水率的标准化序列存在趋势性，采用ADF检验和KPSS检验，分别返回逻辑值0和1，此时不满足平稳序列，现对标准化序列做一阶差分图，见图2。

由图2可知，一阶差分后的序列值在0附近上下波动，序列没有明显的趋势性，此时经ADF检验和KPSS检验，分别返回逻辑值1和0，表明通过检验，一阶差分后的时间序列为平稳时间序列，符合ARIMA建模要求。

2.3 模型选择与定阶

2.3.1 模型选择。

对ARIMA（p，d，q）模型而言，其中p为自回归项，q为移动平均项数，d为差分算子，可以简单理解为当d=0、q=0时，为p阶AR模型，当d=0，p=0时，为q阶MA模型。此次建模对一阶差分后的ACF（即自相关图）与PACF（即Partial PACF偏自相关图）进行拖尾与截尾判断，以此来确定选取合适的模型，判断规则见表1。

一阶差分后的ACF和PACF图见图3，从图中可以看出，ACF与PACF均属于拖尾，应选取ARIMA（p，d，q）模型，同时差分算子d取1。

2.3.2 模型定阶。

由于ACF与PACF均为一阶拖尾，可考虑建立ARIMA（1，1，1）模型，但只进行自相关和偏自相关分析确定p、q的取值存在一定的主观性，为选取最优模型还需结合其他定阶方法。在实际建模中若p、q取值过大，不利于建立合适且准确的模型，这种情况可结合其他方法与策略确定阶数，如EACF法、FPE准则、AIC准则（赤池信息量准则）和BIC准则（贝叶斯信息准则）、 Pandit建模策略等。

此次建模由一阶差分后ACF与PACF图得出p与q的取值范围均为0～1，再采用AIC和BIC准则进一步确定阶数，选取AIC、BIC之和为最小值时的p、q值作为最优模型，结果见表2，此次60 cm深土壤含水量的最优模型为ARIMA（1，1，1）。

2.4 残差检验

为检验选取的阶数是否合适以及对模型进行评价，需对ARIMA（1，1，1）模型进行残差统计分析，做残差ACF与PACF图以及Q-Q分位图，分别检验残差的相关性与分布特征是否为正态分布，见图4～5，由图可知，所有点均在置信区间范围内，大部分点靠近直线，表明残差是随机正态分布且不相关的，为一段白噪声信号。因此该模型可以适用于土壤水分的拟合和预测。

2.5 模型预测

采用2019年5月19日—11月24日28个土壤含水量实测数据作为模型拟合值，对12月份土壤水分进行预测，并绘制土壤水分拟合及预测与实测数据对比图（图6），预测结果误差分析见表3。由图6和表3可知，模型对土壤水分变化拟合程度较好，其中拟合区拟合数据与实测数据的相对误差为0.37%～7.67%，平均相对误差为4.33%。预测区预测数据与实测数据的相对误差为2.83%～5.56%，平均相对误差为4.52%。拟合区与预测区的平均相对误差均小于5%，由此可见，ARIMA（1，1，1）模型可以很好地模拟与预测60 cm土壤水分的变化趋势。

3 结论与讨论

该研究采用三峡库区宜昌市夷陵区仓屋榜柑橘生育期土壤水分实测资料，针对60 cm土壤水分建立ARIMA（1，1，1）模型，拟合区与预测区相对误差分别为0.37%～7.67%、283%～5.56%，平均相对误差分别为4.33%、4.52%，均小于5%。说明该模型可以很好地模拟与预测柑橘根区土壤水分的变化趋势，可以进一步应用在其他作物根区土壤的监测，为农作物优质生长、节水改革提供技术支撑。

该研究采用7 d时段得出三峡库区柑橘品种为蜜橘的根区土壤水分变化规律：柑橘树5月20日左右开始座果，5月19日至6月中下旬土壤水分在20%～25%波动，土壤水分7—9月为果实膨大期，果实对水分需求增大，随着降雨频率的逐渐减小，土壤水分呈波动性下降趋势，下降至15%左右，最终达到稳定，在此阶段应注意适当灌水，积极应对干旱及伏旱，以保证柑橘树正常生长。10—12月为果实成熟期，此阶段土壤水分在10%～15%波动，此时合理灌溉对柑橘品质影响较大，适当减少灌水，可提高果实糖度和耐储性。

ARIMA模型不适合对土壤水分进行长期的预测，但可以持续短期对土壤水分进行预测，需要将新数据不断导入模型训练数据，修正及建立新模型，以得到更加准确、可信的预测数据及时为科学灌溉提供一定理论依据。该研究以周为时间步长采用28个土壤含水量数据作为模型训练数据，得到5个步长的预测数据，预测效果较好。若增加训练数据，可考虑增大短期预测的范围，但仍属于短期预测范畴，这是由于长期预测受其他突变因素影响导致误差叠加所致。为解决这一问题，必然要考虑多变量的因素，同时短期预测的时间范围的临界值尚待进一步研究。

笔者采用28个实测数据拟合，然后做4个步长的预测，再以27个数据，做5个步长的预测，以此类推，直到以20个数据做12个步长的预测，以探索模型训练样本数与预测精度之间的关系，考虑到模型预测的误差会随预测次数增加而变大，因此全部采用4个步长的预测值进行对比分析，最终发现模型预测的平均误差并未明确呈现出随模型训练数据减少而增大的趋势。这可能是因为整体训练样本数不大，以及调整训练样本数做变量的步长较小导致预测精度变化不明显。对于大样本容量的数据，可增大变量的步长，进一步讨论模型训练样本数与预测精度之间的关系。

参考文献

[1] 尚松浩.土壤水分模拟与墒情预报模型研究进展[J].沈阳农业大学学报，2004，35（Z1）：455-458.

[2] 龚元石，李保国.农田水量平衡模型对作物根系吸水函数及蒸散公式的敏感性[J].水土保持研究，1996，3（3）：1-7.

[3] 张雪飞.水量平衡模型在德国奥斯纳布吕克地区和安徽淮北地区对墒情预测的应用研究[D].合肥：安徽农业大学，2013.

[4] 吴姗，莫非，周宏，等.土壤水动力学模型在SPAC系统中应用研究进展[J].干旱地区农业研究，2014，32（1）：100-109.

[5] 康紹忠.土壤-植物-大气连续体水分传输动力学及其应用[J].力学与实践，1993，15（1）：11-19.

[6] 毛晓敏，杨诗秀，雷志栋.叶尔羌灌区冬小麦生育期 SPAC 水热传输的模拟研究[J].水利学报，1998，29（7）：35-40.

[7] 李熙春，尚松浩.华北冬小麦-夏玉米农田水分动态模拟研究[J].灌溉排水学报，2003，22（5）：10-16.

[8] 严昌荣，申慧娟，何文清，等.基于多元回归方法的土壤水分预测模型研究[J].湖北民族学院学报（自然科学版），2008，26（3）：241-245.

[9] 尚松浩，毛晓敏，雷志栋，等.冬小麦田间墒情预报的BP神经网络模型[J].水利学报，2002，33（4）：60-63.

[10] 侯晓丽，冯跃华，吴光辉，等.基于人工神经网络土壤墒情动态预测模型应用研究[J].节水灌溉，2016（7）：70-72.

[11] 武文红，杜贞栋，刘现伟，等.基于BP神经网络的土壤贮水量预报模型研究[J].安徽农业科学，2010，38（15）：8211-8212，8224.

[12] 罗毅，雷志栋，杨诗秀.一个预测作物根系层储水量动态变化的概念性随机模型[J].水利学报，2000，31（8）：80-83.

[13] 张和喜，杨静，方小宇，等.时间序列分析在土壤墒情预测中的应用研究[J].水土保持研究，2008，15（4）：82-84.

[14] 康绍忠.土壤水分动态的随机模拟研究[J].土壤学报，1990，27（1）：17-24.

[15] 刘洪斌，武伟，魏朝富，等.AR模型在土壤水分动态模拟中的应用[J].山地学报，2004，22（1）：121-125.

[16] 杨绍辉，王一鸣，郭正琴，等.ARIMA模型预测土壤墒情研究[J].干旱地区农业研究，2006，24（2）：114-118.

[17] 李军，张和喜，蒋毛席，等.基于ARIMA模型的贵州省黄壤墒情预测研究[J].人民黄河，2010，32（8）：73-75.

[18] 周刘宗，陈志雄，周凌云，等.土壤水分的时序分析研究[J].土壤，1998，30（4）：188-193.

[19] 白冬妹，郭满才，郭忠升，等.时间序列自回归模型在土壤水分预测中的应用研究[J].中国水土保持，2014（2）：42-45.

[20] 路璐，王振龙，杜富慧，等.淮北平原基于ARIMA模型的冬小麦日土壤水分预测[J].节水灌溉，2019（6）：67-71.

[21] 王晓燕，陈洪松，王克林，等.红壤坡地土壤水分时间序列分析[J].应用生态学报，2007，18（2）：297-302.