无人机四元数技术

许景伟，余丽云

（1.中国人民解放军92853部队，辽宁 兴城 125106；2.工业和信息化部电子第五研究所华东分所，江苏 苏州 215011）

0 引言

无人机技术在现代生活中的应用越来越广泛。越来越多的人加入了无人机使用者或设计者行列。但目前大多数无人机爱好者仅仅停留在使用者层次，并且很多无人机爱好者由于缺乏数学基础而无法进阶到初步设计者。因此，对无人机技术有更多、更深入的了解，不管是对无人机爱好者更好地操作无人机，还是有志于进阶无人机设计者进行学习开发无人机技术，都有着极大的帮助。本文着重讨论无人机软件技术中的一个基础算法——四元数法。

1 四元数定义

无人机在空中的姿态问题是所有的无人机软件技术中首要解决的问题。目前常用的无人机姿态定义的方法有欧拉角、旋转矩阵和四元数等[1]。一般无人机姿态定义方法会采用四元数法。因为四元数法相对于另外两种算法有着数据量少、姿态解算快的优点。四元数概念最早由爱尔兰数学家发明，可以把四元数法看作是描述无人机三维姿态的一组向量。

四元数的定义为q=s+xi+yj+z k。i，j，k是单位虚数。复数p=a+bi可以表述二维平面向量，四元数可以简单地认为是一个三维空间的多维复数表示形式，类似复数表示，可定义为

2 四元数在三维空间的旋转

无人机机体坐标系如图1a所示，为B坐标系；地球坐标系如图1a所示，为A坐标系。B坐标系和A坐标系在初始的状态下完全平行或重合，I//X，J//Y，K//Z。为了表示机体坐标系，采用四元数的定义机体姿态为：

其中，cosα、cosβ、cosγ为旋转轴在I、J、K方向的分量，表示机体的姿态旋转方向[2-3]。

如图1b所示，若机体从初始状态开始绕I轴旋转90°，那么机体的四元数表示变化为：

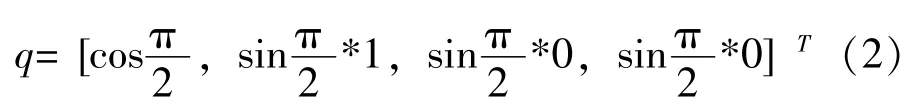
机体旋转定义遵循右手定则（右手大拇指指向旋转轴方向，余下四指自然弯曲方向为正旋转方向）。cosα、cosβ、cosγ在本次旋转中表示为[1，0，0]。

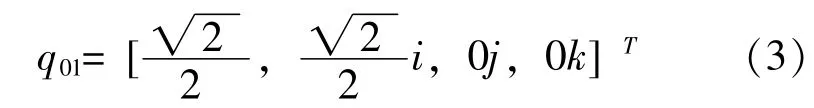
如图1c所示，若机体继续绕I轴旋转90°，那么机体的四元数表示变化为：

此时机体是在前面一次旋转的基础上继续旋转的，不是从初始化位置开始旋转的，得到：

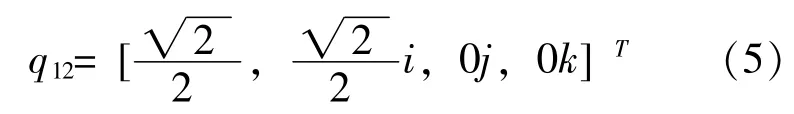
如图1d所示，若机体继续绕I轴旋转90°，可以得：

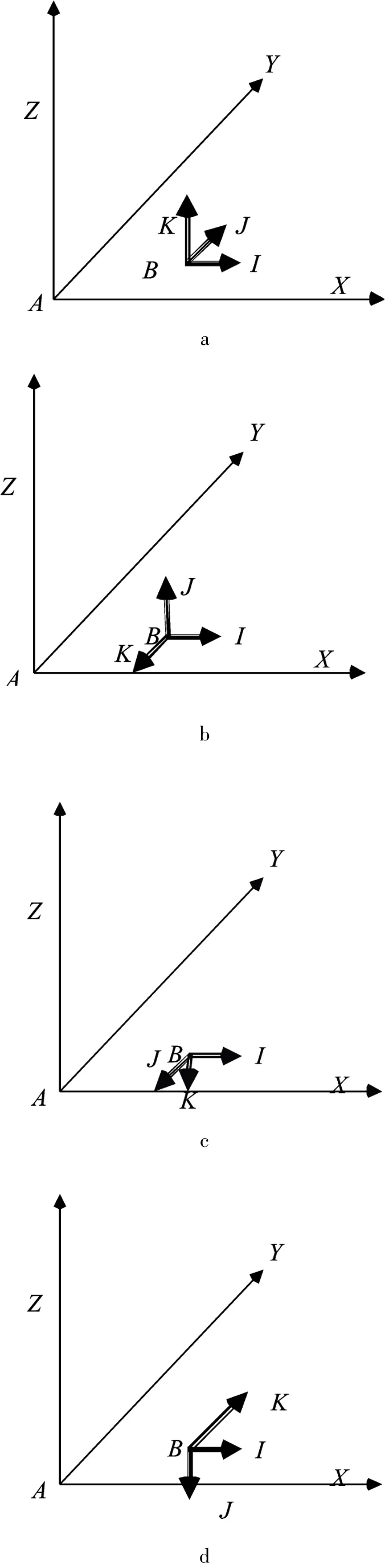
图1 坐标系

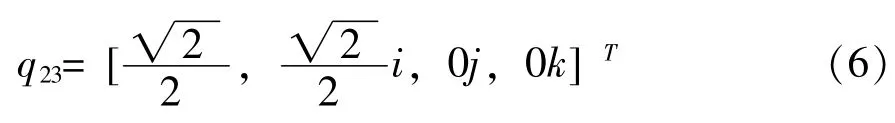
根据四元数的旋转差值计算公式，可以得到3次旋转后的四元数公式为：

若是3次旋转后，继续按原来的规律旋转，那么机体正好旋转一周，可得：

经计算，这和实际情况相符[4-6]。

3 坐标系变换

无人机姿态定义主要是要考虑如何描述无人机在地球坐标系中的相对位置。一般可以把无人机自身姿态定义成一个机体坐标系，如B坐标系；把地球坐标系定义成导航坐标系，如A坐标系。因此无人机姿态定义问题就转变为一个数学问题，即如何在A坐标系中描述B坐标系；或者说如何在B坐标系中描述A坐标系[7]。

显然，通过数学常识，A和B的关系完全可以利用某个运算方式表述，运算方式假定为C，那么可以获得A=BC。由此，进一步可以明确，无人机姿态定义就是为了定义这个C。四元数能完美地表述这个C。

假定机体姿态定义为VB，映射到A坐标系的姿态为VA，根据四元数运算原则，VA=q·VB·q-1。即为：

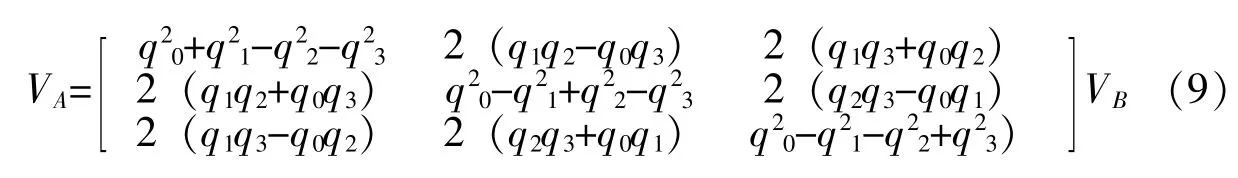
4 四元数姿态解算

对机体姿态进行四元数解算，要结合传感器参数采样更新四元数参数，并采用龙格库塔法更新四元数[4]。可以获得四元数解算更新姿态结果。

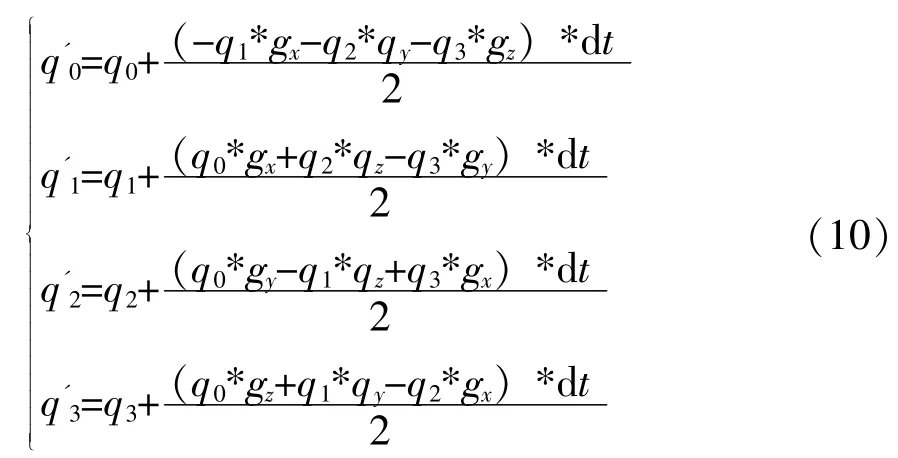
式（10）中：gx、gy、gz——PI迭代计算的误差修正参数。

5 结束语

无人机姿态解算是无人机飞控技术实现的基础，而四元数法无疑是无人机姿态解算的较优方法，对无人机设计者来说需要理解、掌握[8]。即使是无人机使用者，理解四元数法也有助于更好地操控无人机、了解无人机技术。