复杂潮流条件下导管涡轮机的水动力学性能

宋科，杨邦成

(1.昆明学院机电工程学院，云南 昆明 650214; 2.昆明理工大学建筑工程学院，云南 昆明 650500)

近年来，潮流能作为一种清洁可再生能源受到世界各国的重视，尤其在发达国家的能源体系中占据了越来越多的份额[1].水平轴涡轮机作为开采潮流能的一种转换装置，被认为是目前最有前景的开采装备[2].此外，为了有效地提升水平轴涡轮机的输出功率，在其环向加装导管扩散器是一种最直接的方式，得到了国内外学者的广泛关注.BORG等[3]对一种新型导管涡轮机的水动力学性能及尾流场进行了研究.刘垚等[4]研究了导管涡轮机的水动力学性能，发现导管可将涡轮机周围的流速提高1.35倍，转速提高1.2倍，获能效率提高35%.NUNES等[5]对2种不同的导管涡轮机进行了数值模拟和风洞试验，发现导管可以提升涡轮48%～79%的输出功率.TAMPIER等[6]对导管涡轮机进行数值模拟，取得了与试验较为一致的结果，并指出导管与叶轮存在一定的相互作用关系.宋科等[7]从叶轮翼型、叶尖间隙、导管设计参数等方面对一种薄壁导管涡轮机进行了研究.张琰等[8]、郑美云等[9]、KHALID等[10]研究了导管形状对涡轮机的水动力学性能的影响，发现不同的导管形状对于提高涡轮机能量获取性能有很大的影响.BELLONI等[11]使用RANS-BEMT模型分析了导管涡轮机的水动力学性能，并通过文献验证了数值结果的准确性.DÉBORAH等[12]提出了一种优化导管涡轮机叶片设计的新方法，以避免叶片在导管加速流体状态下发生空化.

现阶段对导管涡轮机的研究主要集中在性能设计及均匀流条件下的水动力分析等方面.然而在实际海洋环境中，导管涡轮机不可避免地要在波浪、剪切流、偏流等复杂条件下运行.这将对结构及载体的水动力性能和载荷分布产生不同程度的影响.目前，关于导管涡轮机在上述复杂潮流条件下的水动力问题的相关研究和报道很少，为了填补这一空缺和不足，文中依据斋堂岛海域的潮流条件，探讨浸没深度和偏流角对导管涡轮机的水动力学性能及尾流场流态的影响.希望这项工作能对更好地了解导管涡轮机在复杂潮流条件下的运行状态和为其合理布置提供一定的参考.

1 模型与计算方法

1.1 控制方程

假定流体为不可压缩流体，控制方程分为连续方程及动量方程，雷诺平均Navier-Stokes方程可表示为

(1)

(2)

式中：ui为时均速度；ρ为流体密度；p为流体压力；μ为流体动力黏度；fi为体积力分量.

1.2 水动力学参数

涡轮机的水动力性能可定义为量纲一的系数：叶尖速比TSR、功率系数CP、推力系数CT、叶轮表面压力脉动系数CΔp.

(3)

(4)

(5)

(6)

式中:n为涡轮机转速；P为涡轮机的输出功率，P=M×n/9.55，其中M为扭矩；T为叶轮轴向推力；Δp为表面压力与其平均值之差；A为叶轮旋转扫掠面积；v0为来流流速.

1.3 网格划分与数值验证

导管涡轮机叶轮直径为2 m，计算域中的涡轮机中心距进口5D(D为叶轮直径)，涡轮机中心至出口距离为15D，模型阻塞度小于1.0%.计算域入口设置为速度入口，出口设置为压力出口，外边界条件为自由滑移边界，叶轮及导管为固壁面无滑移壁面条件.将计算域划分为旋转域和静止域，旋转域设置为包裹住叶轮的圆柱体.计算采用SSTk-ω湍流模型，采用滑移网格模型模拟旋转效应，动静交界面采用interface设置，设置叶轮每旋转1.8°作为1个时间步长(0.005 s)，每步的计算残差收敛最小值小于10-3.假设来流速度为1.56 m/s，参考长度为叶轮半径(1 m)，则系统的雷诺数约为1.6×106.对叶轮及导管进行网格加密，叶轮第1层边界层网格满足Y+=1条件，导管第1层边界层网格满足Y+=10条件.计算域及网格如图1所示.对导管涡轮机在1.56 m/s和60 r/min条件下进行网格数无关性验证，如表1所示，当网格数N超过600万后，CP和CT基本不变.最终划分网格总数约为630万，其中旋转域为170万，静止域为460万.

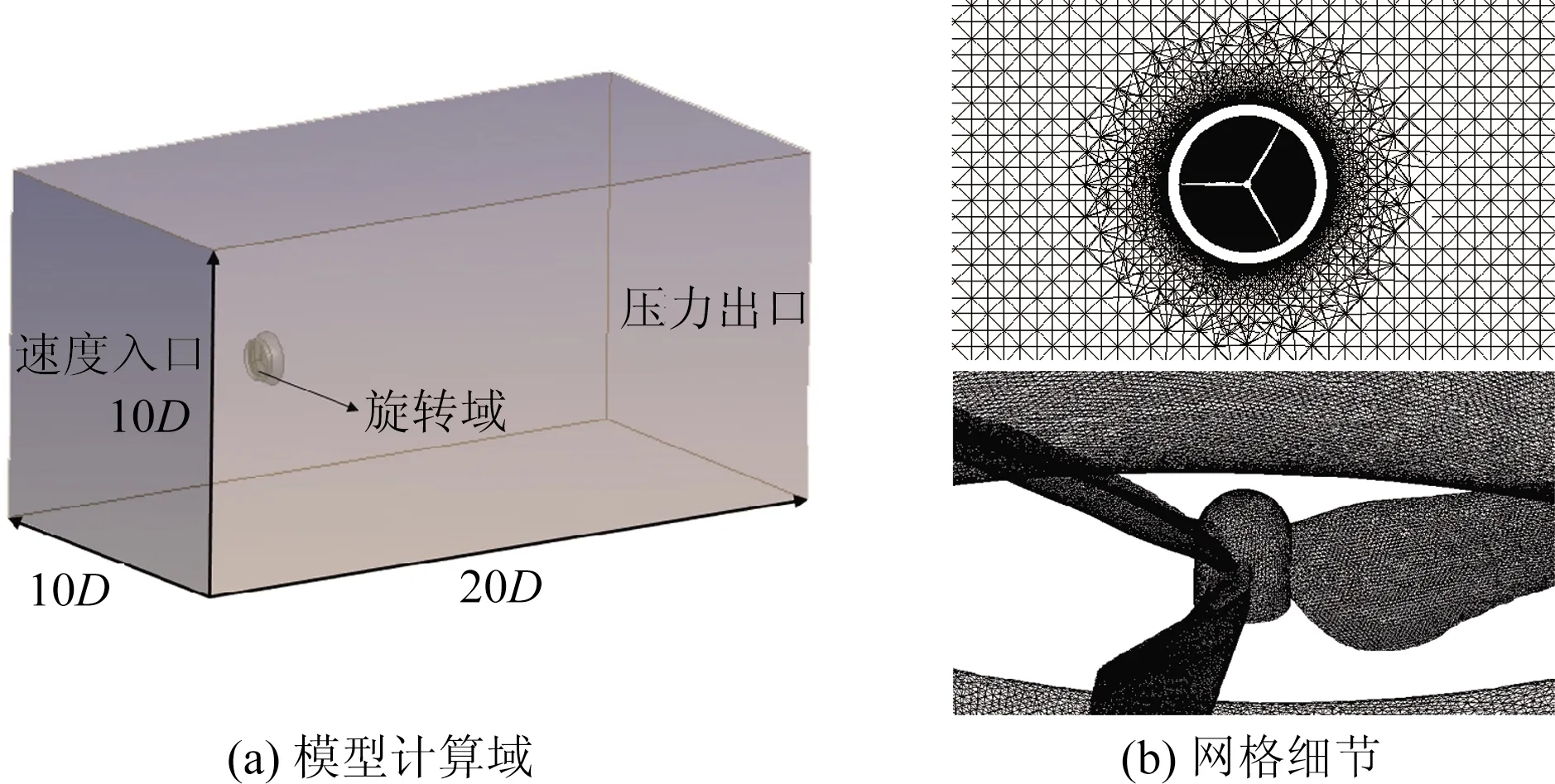
图1 计算域及网格

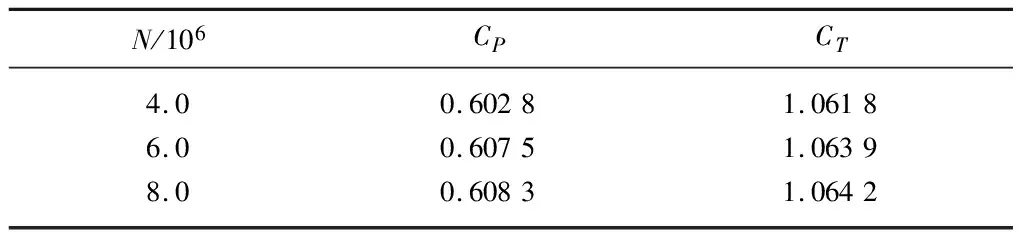
表1 网格数无关验证

为了确保数值模拟的准确性，对叶轮的CFD计算结果与功率系数试验值[13]进行比较.其中，该试验为一拖拽水池试验，在5种不同的拖拽速度下对试验叶轮的输出功率进行了测试.5种速度v下的CFD计算结果与试验值的对比如图2所示，由图可以看出，两者吻合度较好，验证了文中数值模型及方法的可靠性.

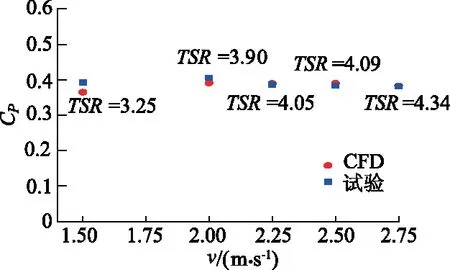
图2 试验与CFD对比结果

1.4 地理背景与潮流条件设置

青岛斋堂岛海域是中国比较有代表性的潮流能资源区之一，依据该海域实际潮流条件作为研究背景，其日常极限波浪参数为波高0.6 m，波长24.8 m，波浪周期为3.2 s，水深h与流速的关系[14]如图3所示.可以看出，流速随水深的增加而减小，水深为0～10 m(5D)时的流速约为1.56 m/s，此外，水深为0～15 m(7.5D)时的流速梯度约为0.002.依照地理数据，将速度入口条件设置为(1.56±0.002h)m/s(导管涡轮机轴切面处的速度为1.56 m/s，h=0)，导管涡轮机转速为60 r/min.此外，按照上述波浪条件和文献中的设置方法[15]，引入多相流模型VOF来模拟波浪作用.

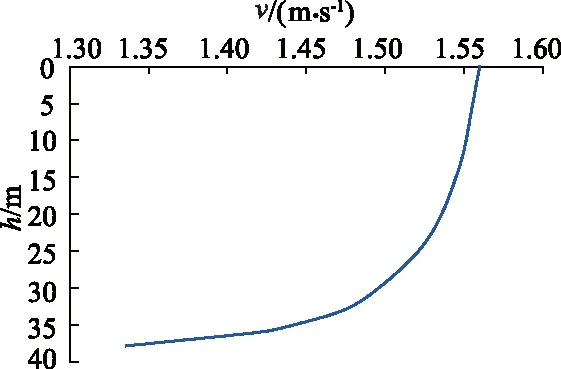
图3 水深与流速关系

2 结果与分析

2.1 浸没深度的影响

导管涡轮机轮毂在不同浸没水深下(2D，3D，4D)的CP，CT和CΔp随时间变化曲线如图4所示.可以看出，波流引起的效应随浸没深度衰减.当浸没深度为3D时，导管涡轮机最大瞬时CP，CT和CΔp分别比4D时增加了8.0%，4.5%和132.0%；当浸没深度为2D时，导管涡轮机最大瞬时CP，CT和CΔp分别比4D时增加了25.0%，13.0%和313.0%.由此可以看出，波流条件下浸没深度对导管涡轮机水动力性能的影响很大.在同一波流条件下，浸没深度越小，CP，CT和CΔp波动幅度越大，且浮动值远超纯流条件下的.

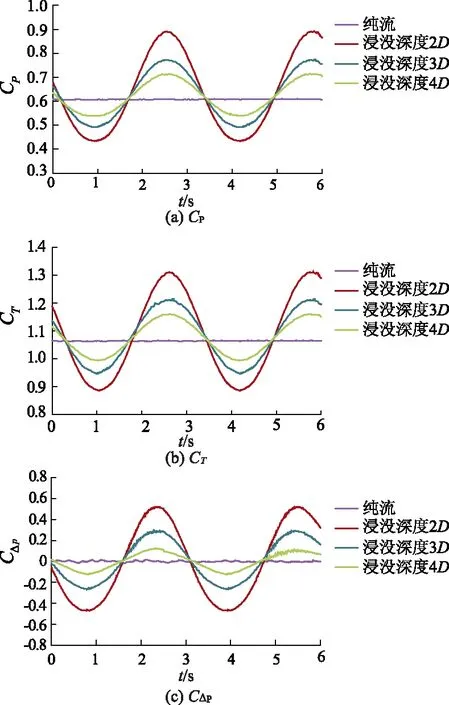
图4 不同浸没深度下CP，CT，CΔp随时间变化曲线

同时，还可以看出，在波流条件下，CP，CT和CΔp表现出与波浪频率一致的时间周期性行为，波峰通过时导管涡轮机产生最大功率，波谷通过时产生最小功率.此外，3种浸没深度下与纯流条件下导管涡轮机的平均CP，CT非常接近，说明波浪的效应基本不会影响导管涡轮机的时均输出功率和轴向推力.导管涡轮机在3种浸没深度下，不同下游位置的流向速度截面分布如图5所示(t=6 s，当涡轮机处于波浪的波峰附近时刻).

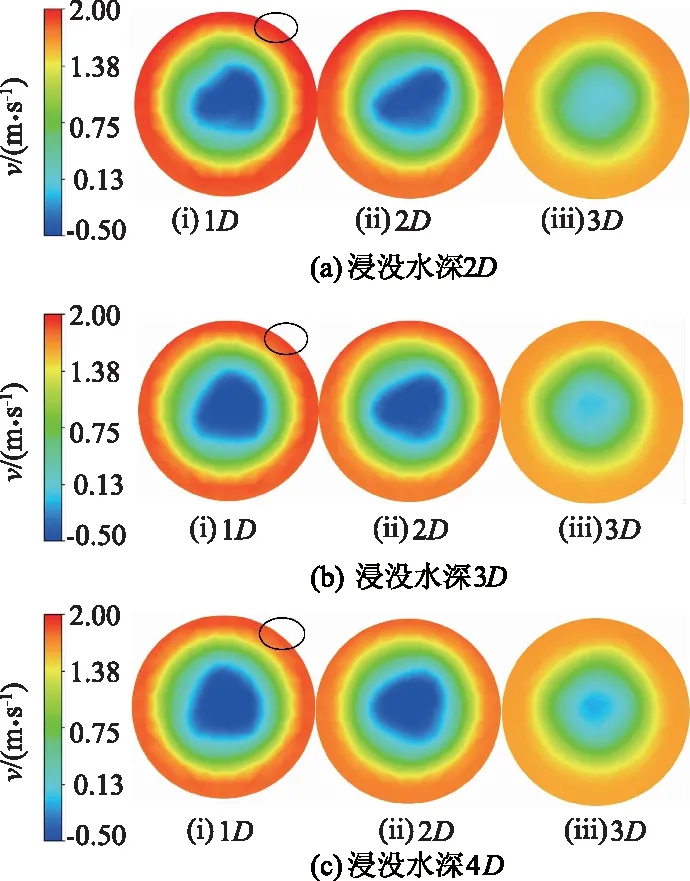
图5 不同浸没深度下的流向速度截面分布

由图5可以看出，叶轮旋转与波流共同作用对导管涡轮机尾流区域流态的影响，在1个波流周期内的尾流场周边流速经历1个不断变化的过程.当波峰通过时，将诱导尾流加速向上，波谷则相反，导管涡轮机的尾流结构在1个波流周期内是不断地被抬高和抑制的.

此外，在波浪的作用下，水-气交界面整体变形较大，将引起明显的流速跃迁变化.因此，当浸没水深较浅时，水流将发生强烈的跃迁，波流的振荡效应也将变得十分明显，叶轮扫掠区域后方周围的流场流速较快(体现在云图中颜色较深，圈出部位).随着浸没深度的增加，流速的迁移效果逐渐减弱，对扫掠区域后方附近的流场的影响也逐渐减小.这也解释了越靠近水面对导管涡轮机CP，CT和CΔp的影响越明显的原因.

2.2 偏流的影响

通过调整导管涡轮机的角度来模拟不同偏流角下的水动力学性能.导管涡轮机(浸没深度为3D)在不同偏流角(30°，45°，60°)的CP，CT和CΔp随时间变化曲线如图6所示.可以看出，CP,CT和CΔp表现出与波浪频率一致的时间周期性行为.同时，随着偏流角的增大，流向上的扫掠投影面积越来越小，水流动能逐渐由轴向分量转移至侧向分量，导管涡轮机的平均CP和CT逐渐减小.同时，由于偏流角的变化改变了涡轮机叶片原本叶素截面的局部相对攻角分布，这也影响了涡轮机的能量捕获能力和推力.导管涡轮机在30°时的平均CP,CT分别比无偏流时减小13%，10%；在45°时的平均CP,CT分别比无偏流时减小了48%和34%；在60°时的平均CP,CT分别比无偏流时减小了88%和64%.可见，在大偏流角下导管涡轮机的CP，CT有1个明显的下滑[16].

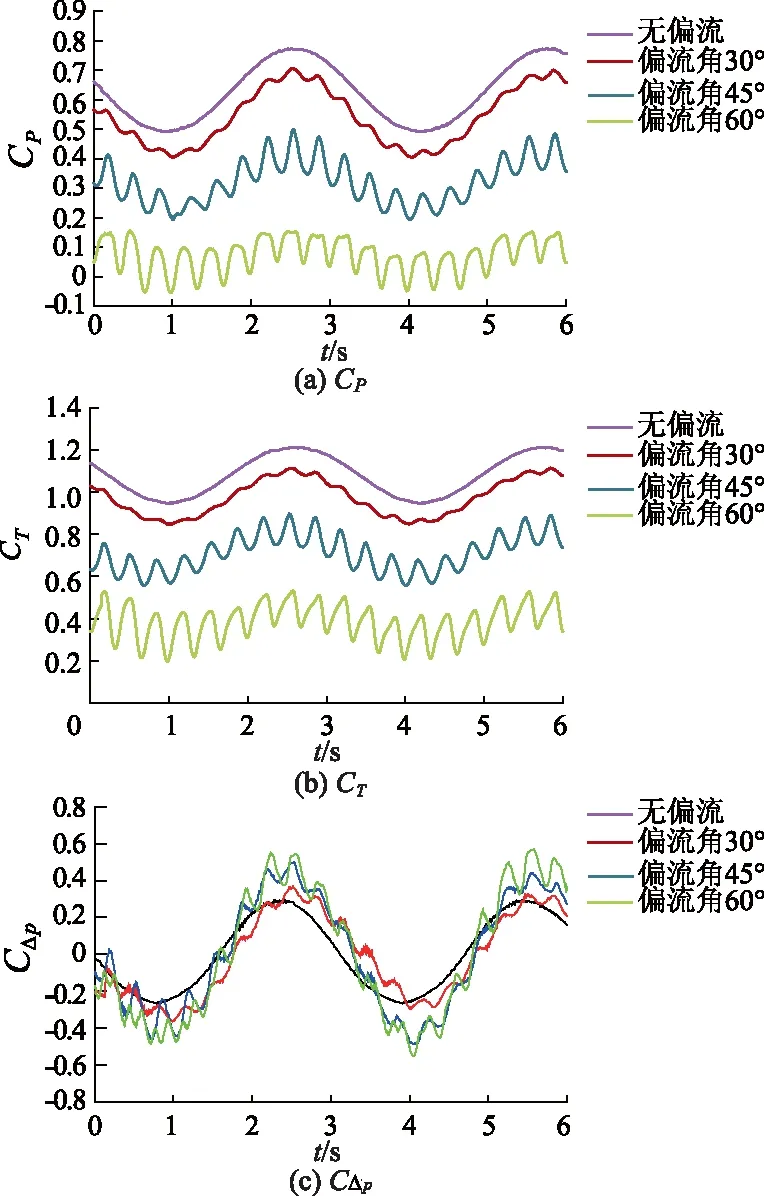
图6 不同偏流角下CP,CT,CΔp随时间变化曲线

由于偏流的不对称性使叶轮前后两端的压力差始终处于不稳定的状态，导致CP，CT和CΔp在波浪周期内出现额外的周期性波动，该波动频率由转速和叶片数决定.叶轮的旋转周期为1 s，叶片数为3.当1个叶片正好处于竖直位置时，CP，CT和CΔp则处于额外周期的波峰处；而当1个叶片正好处于水平位置时，CP，CT和CΔp则处于额外周期的波谷处[17]，因此导管涡轮机在1个时间周期内要经历3次额外的周期性波动.随着偏流角的增大，该额外周期性波动的振幅也逐渐增大.在偏流角为30°时，CP，CT和CΔp的额外周期性波动最大振幅分别为0.041,0.033和0.087.在偏流角为45°时，CP，CT和CΔp的额外周期性波动最大振幅分别为0.151，0.155和0.128.在偏流角为60°时，CP，CT和CΔp的额外周期性波动最大振幅分别为0.205，0.282和0.218.因此，导管涡轮机叶片在波流与偏流共同作用下将承受极高的压力梯度和由此带来的水动力不平衡力的影响.

导管涡轮机在3种偏流角下不同下游位置的流向速度截面分布如图7所示(t=6 s，当涡轮机处于波浪的波峰附近时刻).

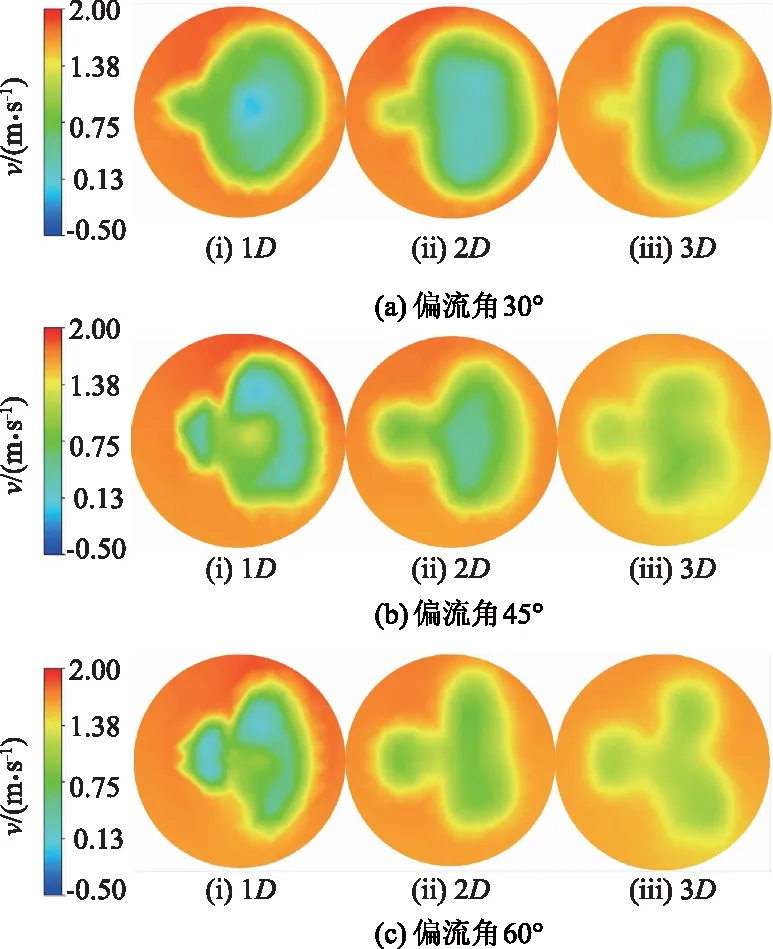
图7 不同偏流角下的流向速度截面分布

水流通过导管涡轮机后将被诱导分离为轴向与侧向分量，只有轴向分量有利于导管涡轮机的能量捕获.这种由偏流导致的速度变化，也成为决定导管涡轮机水动力载荷的因素之一.由图7可以看出，导管涡轮机在偏流条件下的尾流都发生了侧向的偏移和变形，呈现出非对称流动结构.随着偏流角的增大，下游流场结构变得相当不稳定和复杂.在30°偏流角下，尾流分布近似于一种椭圆的几何形状.当偏流角为45°和60°时，尾流被分离成2个低速区，此时尾流分布已无特定形状可言.值得一提的是，随着偏离角的增大，尾流恢复逐渐加快.

3 结 论

根据斋堂岛海域条件对导管涡轮机在复杂波流条件下进行了数值模拟研究，探讨了浸没深度和偏流角对其水动力学性能的影响，得出以下主要结论：

1)在波流作用下，随着浸没深度的减小，水流将发生强烈的跃迁，波浪效应增强，叶轮扫掠区域后方附近的流场流速加快，波流引起的CP，CT和CΔp振幅增大.当波峰通过时产生最大值，波谷通过时产生最小值.此外，导管涡轮机在3种浸没深度下与纯流条件下的平均CP，CT非常接近.

2)在波流与偏流共同作用下，随着偏流角的增大，流向上的扫掠投影面积越来越小，水流动能逐渐由轴向分量转移至侧向分量，导管涡轮机的平均CP和CT逐渐减小.此外，下游的尾流结构都发生了侧向的偏移和变形，呈现出非对称流动结构，且随着偏流角的增大，流场结构将变得相当不稳定和复杂，但尾流恢复逐渐加快.

3)处于不同浸没深度及偏流角的导管涡轮机CP，CT和CΔp均表现出与波浪频率一致的时间周期性行为.此外，偏流将导致CP，CT和CΔp在叶轮旋转周期内出现额外的周期性波动，该波动频率由转速和叶片数决定，且波动幅值随着偏流角的增加而增大.