透平增压泵轴承-转子系统动力学特性

潘慧山，蒋小平,2*，郎涛，周晨佳，曹玲，张德胜，胡敬宁

(1.江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013；2.南京农业大学国家信息农业工程技术中心，江苏 南京 210095)

透平增压泵将透平叶轮与增压叶轮集成到同一个转子上，具有效率高、结构紧凑、维修保养方便等诸多优点，逐渐成为国内外海水淡化装备研究的热点[1-2].透平增压泵一般采用水润滑轴承作为转子系统的主要径向支承，转速的急剧提升往往导致轴承阻尼的迅速下降[3-5]，同时，作用在透平叶轮与增压泵叶轮上的流体激励力等也对轴承-转子系统的稳定性产生严重影响，迫切需要对透平增压泵的转子系统进行深入研究以确保海水淡化系统的安全可靠运行[6-7].

近年来，随着旋转机械尤其是航空航天动力设备不断朝着高速化方向发展，高速转子系统的动力学稳定性显得尤为重要.已有诸多学者对高速转子的动态稳定性开展了研究.WANG等[8]通过有限元建模以及瞬态响应分析发现，通过改变不平衡质量的位置可以有效减小或抑制高速涡轮增压器转子的振动.洪杰等[9]通过仿真计算，提出了高速转子支承结构及力学特性优化的设计方法；郑昂等[10]通过分析轴承的润滑特性及转子的动力性能发现通过增加轴承宽度可以提高轴承的承载性能，进而提高高速泵运行的稳定性.段小辉等[11]通过Samcef Rotor软件对高速泵转子进行了临界转速计算，使设计转速远离转子的临界转速，以避免发生共振.

以上研究主要集中在短滑动轴承支承的转子系统，对于长滑动轴承高速转子系统相关研究则鲜有报道.文中通过理论建模、有限元计算与瞬态动力学分析，探究海水淡化透平增压泵水润滑轴承-转子系统的临界转速、瞬态响应等转子动力学特性，为提高转子系统与机组的稳定性以及工程应用等提供有益参考.

1 水润滑轴承-转子系统的建模

1.1 转子物理模型

图1为海水淡化液力透平增压泵的二维结构设计图.其中，转子本体主要由1根长为128 mm的阶梯轴与安装在轴上的增压泵叶轮、透平叶轮这3部分构成.增压泵叶轮中，进口直径、出口直径、出口宽度和轮毂直径分别为56，88，10和25 mm；透平叶轮中进口直径、出口直径、出口宽度和轮毂直径分别为40.0，85.0，6.5和14.0 mm；主轴长度和最大轴径分别为128和35 mm.

由上述参数计算分别得到转子各部件的质量、转动惯量等参数，其中，透平叶轮的质量、极转动惯量和直径转动惯量分别为0.788 m/kg，636.5 kg·mm2，385.6 kg·mm2；增压泵叶轮的质量、极转动惯量和直径转动惯量分别为1.283 m/kg，1 117.0 kg·mm2，1 297.0 kg·mm2；主轴的质量、极转动惯量和直径转动惯量分别为0.806 m/kg，1.25 kg·mm2，9.02 kg·mm2.

考虑到工作介质为海水，转子各部件材料均选用密度为7.8 g/cm3、弹性模量为206 GPa、泊松比为0.26的超级双相不锈钢(轴为锻件).

1.2 轴承模化及动特性系数求解

轴承作为转子系统中阻尼的主要来源，对转子的临界转速和稳定性有显著影响.轴承模化和动特性系数求解是轴承-转子系统建模的关键.对于滑动轴承而言，当轴颈在静平衡位置上受到位移或速度扰动时，液膜对于轴颈的反作用力就会发生变化，力的变化和扰动之间的关系一般是非线性的.为了方便研究，一般将液膜力按式(1)进行线性化处理[12].

(1)

若将单位位移引起的液膜力增量定义为液膜刚度系数，单位速度引起的液膜力增量定义为液膜的阻尼系数，则可得到轴承的8个动特性系数为

(2)

由此，水润滑轴承即可模化为图2所示的一个由4个刚度系数和4个阻尼系数组成的弹性阻尼支承.其中Kxx，Kyy和Cxx，Cyy为主刚度系数和主阻尼系数；Kxy，Kyx和Cxy，Cyx为交叉刚度系数和交叉阻尼系数，它们表示液膜力在2个互相垂直方向的耦合作用.

图2 水润滑轴承的动力学模型

对于圆柱水润滑轴承动特性系数的求解，通常采用在轴承静平衡位置上添加微小扰动来计算液膜力增量的办法[13].当介质黏度为常数时，轴承液膜的量纲一化非定常雷诺方程为

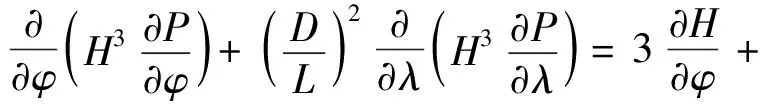
6(x′sinφ+y′cosφ)，

(3)

式中：H为量纲一的膜厚；D为轴承直径；L为轴承长度；P为量纲一的压力；φ为液膜周向角；λ为轴向步长；x′，y′为量纲一的速度扰动参数.

由非定常雷诺方程解得静平衡位置的液膜压力分布，积分后对扰动参数求导，即可得刚度系数和阻尼系数的表达式[12]为

(4)

(5)

液力透平增压泵所用的水润滑轴承长度L=42 mm，主轴轴径D=35 mm，轴承半径间隙c=0.2 mm，水的动力黏度系数μ=1.01×10-3Pa·s.根据转子各部件的质量信息，可以求得转子所受重力为28.2 N，即轴承的静态支反力f为28.2 N.通过Matlab软件编程，计算得到了设计转速16 000 r/min下水润滑轴承的8个动特性系数，其中刚度系数中Kxx=437 N/mm，Kxy=149 N/mm，Kyx=1 015 N/mm，Kyy=1 718 N/mm;阻尼系数中，Cxx=202 N·s/m，Cxy=307 N·s/m，Cyx=306 N·s/m，Cyy=1 174 N·s/m.

1.3 转子系统有限元模型

将液力透平增压泵转子的三维实体模型导入Samcef Rotor软件中，在Analysis Data模块下定义转子系统的材料特性并设置转子信息.结合前文对轴承单元的简化分析，在软件中用弹簧单元模拟轴承，得到水润滑轴承-转子系统的三维计算模型，见图3.将模型沿着轴线从左往右划分成由透平叶轮、轴段、水润滑轴承和增压泵叶轮等单元组成的离散模型，并以节点来代替各单元.对节点从左往右进行编号，得到如图4所示的轴承-转子系统的一维梁-弹簧-集中质量模型.

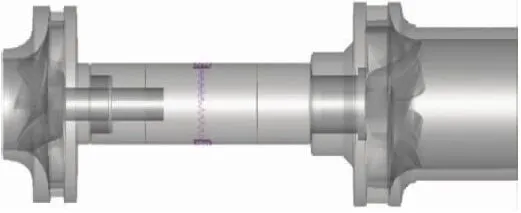
图3 轴承-转子系统有限元模型

图4 一维梁-弹簧-集中质量模型

2 临界转速计算与分析

当旋转机械的工作转速在其临界转速的分布范围内时，机械会产生剧烈振动，严重时系统会遭到破坏，因此计算转子的临界转速是转子系统动力学分析的关键之一[14].选择图3所示的三维有限元模型进行临界转速计算.设置求解器类型为critical speed & stability.对模型进行网格划分，叶轮和轴均采用四面体网格，网格总数为34 449.设置求解临界转速的计算方法为伪模态法，扫频范围为0～6 000 Hz，扫频次数为200.

图5为液力透平增压泵轴承-转子系统前4阶模态的坎贝尔图.可以看出，转子系统的各阶涡动频率fw有明显分叉，这是因为转子系统受陀螺力矩的影响，正进动时涡动频率随转子自转角速度的增大而升高，反进动时涡动频率随转子自转角速度的增大而降低.由坎贝尔图能够计算出转子的临界转速nc.图5中各阶正向涡动频率线与附加的h线的交点处所对应的转速即为转子的各阶临界转速.通过处理得到表1所示的转子系统前4阶临界转速.透平增压泵的设计转速为16 000 r/min，小于第1阶弯曲临界转速，说明该转子为刚性转子.

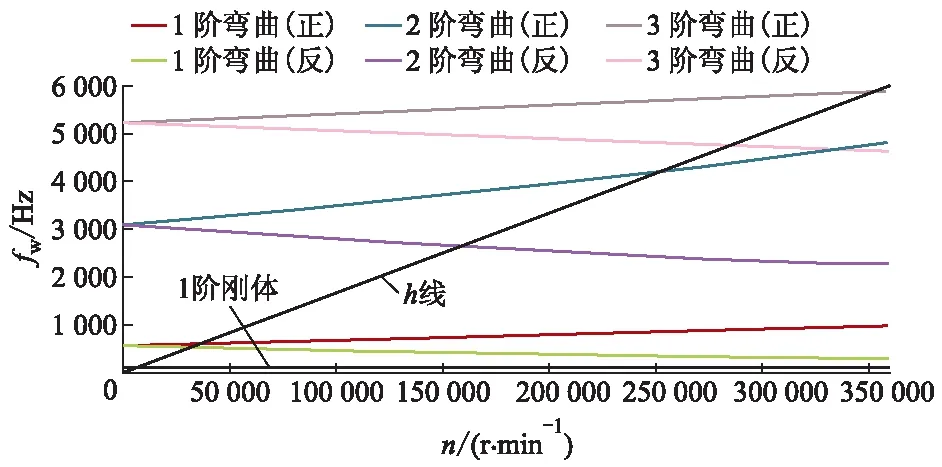
图5 考虑陀螺效应的坎贝尔图

表1 转子前4阶临界转速

设计转速下转子的前4阶振型如图6所示.可以看出，转子的第1阶振型是典型刚体模态，但不是单一的平动(圆柱)或转动(锥形)，而是平动和转动的耦合振型，转子整体的位移较大.后3阶振型为弯曲模态，第1阶弯曲模态轴段表现出微小的弯曲，叶轮无变形；第2阶弯曲模态轴段弯曲变形加重，透平叶轮有较小变形；第3阶弯曲模态轴段呈S状，透平叶轮和增压泵叶轮均严重变形.

图6 转子前4阶模态振型

3 轴承-转子系统瞬态响应分析

当轴承-转子系统受到外部激励作用时，轴心会发生严重影响系统稳定性的位置突变.通过瞬态动力学响应，可以分析确定外部激励力作用下轴承-转子系统的位移、应变、应力等参数的时间历程变化规律.这里研究2种情况，即仅考虑转子不平衡质量，以及同时考虑转子不平衡质量与流体激励力2种情况下转子系统的瞬态响应情况.

3.1 流体激励力计算

作用在转子上的流体激励力主要以透平叶轮和增压泵叶轮上所受到的径向力形式存在.利用Creo软件对增压泵和透平的计算域进行三维造型，得到图7所示的计算域模型.通过ICEM软件对透平和泵的流体域进行网格划分，生成四面体非结构化网格.针对增压泵和透平的设计流量，进行扬程的相关计算，当增压泵的网格数量达到3 563 797，透平的网格数量达到2 612 692后，网格数量对扬程的影响可以忽略不计，说明此时的网格数量已经满足计算精度要求.

图7 透平和增压泵流体域模型

流场数值计算在CFX14.5中进行，先进行定常计算，湍流模型选择k-ε模型.进口边界条件采用总压进口，其中增压泵的进口总压为3.5 MPa，透平的进口总压为5.5 MPa.出口边界条件设置为质量流量出口，设计流量工况下增压泵的出口流量为25.72 kg/s，透平的出口流量为14.14 kg/s.设置求解总步数为3 000，时间步长为0.003 75 s，残差收敛精度为10-4.在定常计算收敛的基础上，把定常结果作为非定常计算的初始条件，进行非定常计算.非定常计算总计算时长为5个叶轮旋转周期，即0.018 75s.通过计算，分别得到了如图8所示的0.8Qd，0.9Qd，1.0Qd，1.1Qd以及1.2Qd流量工况下透平叶轮和增压泵叶轮的径向力分布.可以看出，透平叶轮的径向力随着流量的增加而增大，0.8Qd时径向力最小，这是因为透平在设计时采用了偏小流量设计的方法.增压泵叶轮的径向力随着流量的增加先减小后增大，由于增压泵在1.1Qd流量工况下取得最高效率，因此在1.1Qd时增压泵叶轮的径向力取得最小值.此外，2个叶轮所受的径向力均呈明显的周期性变化，变化周期与叶轮叶片数呈正相关.

图8 叶轮径向力分布图

3.2 考虑不平衡质量的瞬态响应分析

对图4所示的一维梁-弹簧-集中质量模型进行瞬态响应分析.在透平叶轮和增压泵叶轮上各添加质量为0.5 g、偏心距为4 mm、相位为45°的不平衡质量单元.设置叶轮转速随时间线性递增，转速变化为0到16 000 r/min，所需时间为1 s，总计算时间设为1.5 s.分别在考虑轴承阻尼和忽略阻尼的情况下进行转子加速时间历程的瞬态响应分析，得到轴承处节点的瞬态响应如图9所示.

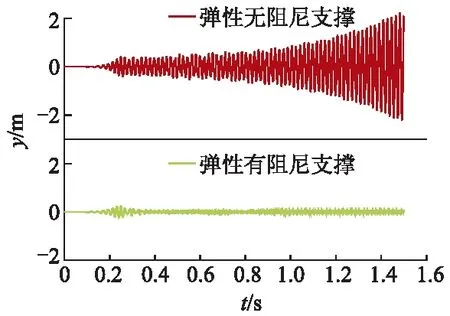
图9 不同支承下转子的瞬态响应图

从图中可以看出，转子系统升速过程中，y方向(旋转轴为x轴)的振动幅值有1次激增，对应的转速约为3 600 r/min，与转子系统第1阶刚体模态临界转速3 568 r/min相接近.在忽略轴承阻尼时，转子系统经过共振区后振幅持续增大，转子失稳.在考虑轴承阻尼时，转子系统可以顺利越过共振区，振幅逐渐衰减并最终达到稳定状态，说明轴承阻尼对转子振动起到较好的衰减作用.

图10为不平衡质量分别加载于各节点位置时转子系统的不平衡响应结果.从图中可以看出，不平衡质量施加于不同位置时，整个轴系越过刚体模态时的共振幅值不同，最大振幅出现在透平叶轮处，与第1阶刚体模态的振型相对应.当不平衡质量处于透平叶轮上时，转子系统的共振幅值大于不平衡质量处于增压泵叶轮上时，说明转子系统对于透平叶轮上的不平衡质量更加敏感.因此透平叶轮的动平衡试验应采用更高的平衡精度等级.

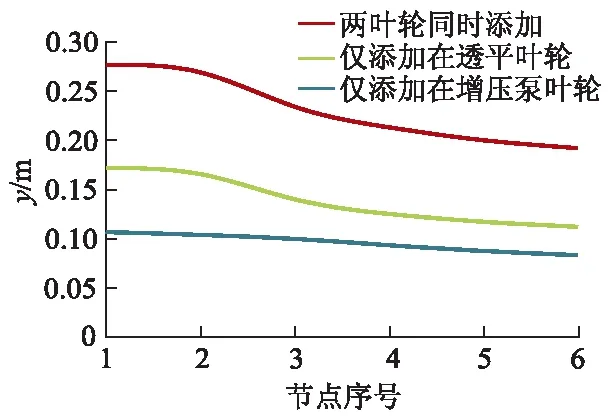
图10 不同偏心下各节点共振幅值曲线

3.3 考虑流体激励力的瞬态响应分析

在透平叶轮和增压泵叶轮上添加不平衡质量单元的同时将3.1节计算的径向力加载到各自叶轮上.设置转子在设计转速16 000 r/min下恒速运转，从0.2 s开始加载叶轮径向力，总计算时间设置为0.4 s.以对外载荷激励敏感程度更高的透平叶轮处的节点作为监测点，得到该监测点处的瞬态响应结果如图11，12所示.

从图11中可以看出，与仅考虑不平衡质量时的转子瞬态响应分析结果相比较，在施加叶轮径向激励力后，转子系统的径向位移明显加大.在仅考虑不平衡质量作用时，转子的轴心轨迹呈规则的椭圆状；在考虑径向激励力后，轴心轨迹呈花瓣形椭圆，且不同流量工况下的轨迹偏心情况不同，轨迹曲线复杂.

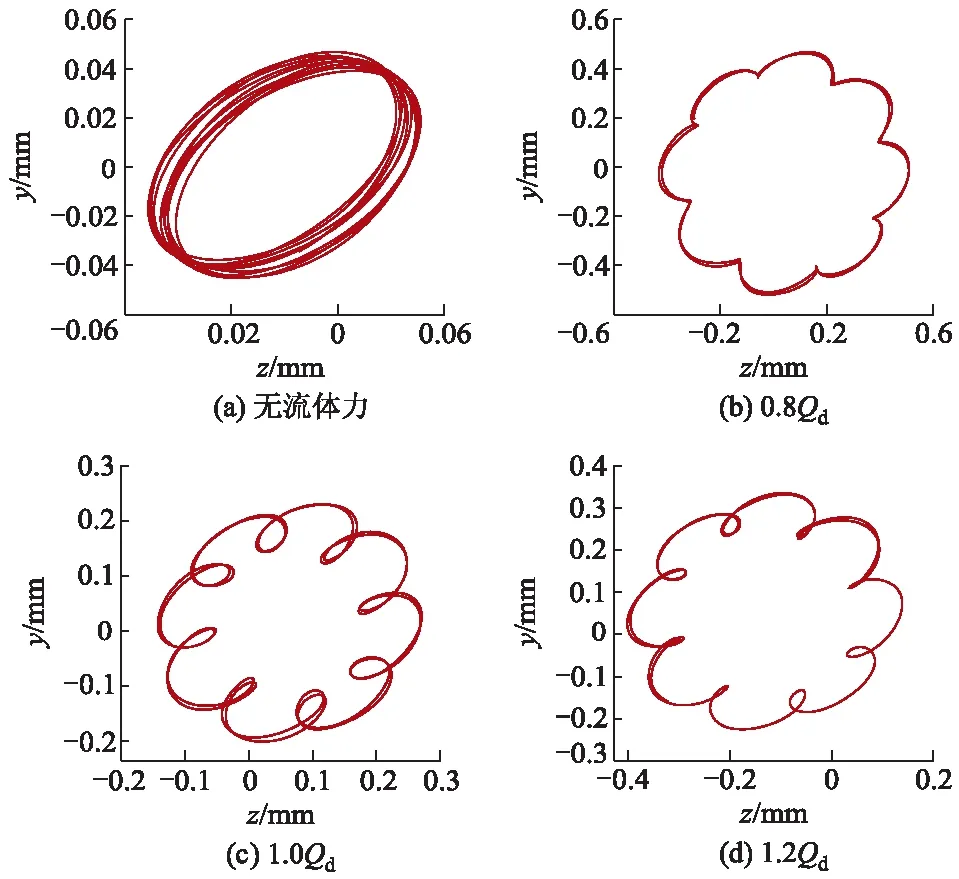
图11 不同工况下的轴心轨迹曲线

从图12中可以发现，不同流量工况下，转子系统因受到的径向力不同，振幅A也有所不同.转子系统的振动呈明显周期性变化，振幅的波动周期约为转子旋转10圈所需时间(37.5 ms)，说明转子的振动频率与轴频相关.每个周期内有8个小波峰，正好与图11中轴心轨迹的8个花瓣形波动相对应.在设计流量工况1.0Qd下，转子振幅最小，且幅值波动较为平稳，说明设计工况下转子运转最稳定.

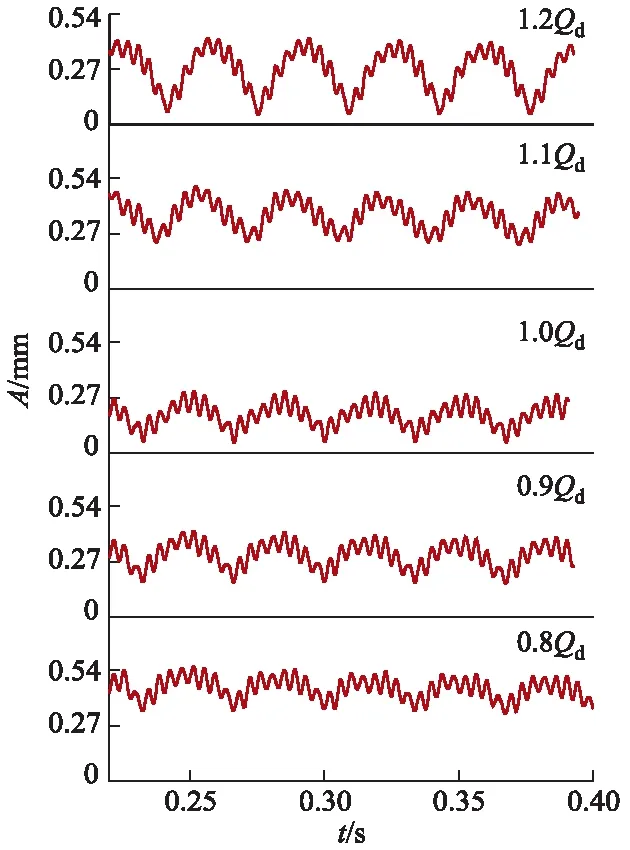
图12 同时考虑不平衡质量和流体激励力的瞬态响应图

4 结 论

1)在16 000 r/min的设计转速下，液力透平增压泵转子属于刚性转子；转子第1阶模态振型为刚体平动和转动的耦合振型，后3阶模态振型为弯曲振型.

2)设计参数下的轴承阻尼能够帮助转子顺利通过其第1阶刚体模态，说明该水润滑轴承能够满足液力透平增压泵转子稳定运转的要求.

3)液力透平增压泵转子系统对透平叶轮上的不平衡质量敏感程度更高，与增压泵叶轮相比，透平叶轮应在动平衡试验时采用更高的平衡精度等级.

4)透平叶轮与增压泵叶轮的径向力随流量变化呈不同规律变化，径向力激励下转子系统的振动明显加强，轴心轨迹呈明显花瓣形椭圆，且设计流量工况1.0Qd下转子振幅最小，运转最稳定.