小型闸站式侧向泵站进水流态数值模拟研究
罗灿,雷帅浩,袁尧,成立,杜康
(1.扬州大学水利科学与工程学院,江苏 扬州 225009;2.江苏省水利科学研究院,江苏 扬州 225000)
最新《全国水利发展统计公报》显示,全国大中型泵站有4 652座,约占4.87%,其他皆为小型泵站.对于小型泵站而言,进水系统采用进水池居多.为了获取良好的进水条件,进水池前需设置前池.当地形条件受限时,采用侧向进水前池,其水流与进水池水流方向不一致,池内易形成回流、旋涡等不良流态[1].针对侧向进水前池和进水池内的不良流态,国内学者做了大量的研究工作.资丹等[2]采用数值模拟和现场测试的方法分析了组合式导流墩在大型泵站前池和进水池流态改善的作用;罗灿等[3]采用数值模拟和试验研究的方法分析了导流墩在非对称式闸站结合式泵站前池的整流效果;徐波等[4]采用数值模拟的方法研究了导流墩几何参数对闸站合建枢纽通航水流条件的影响;冯建刚等[5]通过水力模型试验发现,在前池布设导流墩可有效地改善池内流态;成立等[6]开展了Y形导流墩几何参数对前池流态改善效果的数值模拟研究;徐存东等[7]采用数值模拟的方法分析了压水板对前池流态的改善作用;于永海等[8]利用数值模拟的方法分析比较了导流板几何参数对前池的整流效果.这表明导流板和导流墩在池内改善中都具有重要的作用,但采用导流板和导流墩进行联合整流的研究较少.
某泵站设计流量为6 m3/s,根据《泵站设计规范》,该泵站为小(1)型泵站[9].该泵站将船闸和泵站合建,为典型的闸站式泵站,泵站前池兼顾通航功能,若涉及整流,无法在前池中布设整流措施.因此,文中围绕泵站进水池内存在的不良流态,设置不同的整流措施,并对其整流效果展开数值模拟分析,研究结果可为同类泵站流态的改善提供参考.
1 数值计算方法
1.1 控制方程
文中将水作为不可压缩流体,进水池内的雷诺数Re=4.4×105,因此泵站进水池内的流动为充分发生的紊流.忽略热能量交换,采用包括连续性方程和动量方程在内的RANS控制方程去描述该流动,同时采用RNGk-ε湍流模型对方程进行封闭,离散方程组采用分离求解器进行求解.连续性方程和动量方程分别为
(1)
(2)
式中:ui,uj为各方向速度分量;xi,xj为坐标分量;p为压力;ρ为水体密度;g为重力加速度;v为水体运动黏性系数;vt为湍动黏性系数.
1.2 计算域
该泵站共有4台机组,两侧各有1个备用进水池,每个进水池内设1台轴流泵机组,单泵设计流量为1.5 m3/s,泵站设计流量为6 m3/s.计算域包括前池、进水池和进水管,如图1所示,图中D为进水管直径,喇叭管进口直径为1.4D,进水管悬空高(进水管口至底板的距离)为D,后壁距(进水管至后壁的距离)为D,水深为4D,进水池水下体积为单泵设计流量的71.42倍,完全符合设计规范,沿前池水流方向将进水池依次标记为1#—4#.

图1 计算域示意图
1.3 边界条件设置
取水流进水处为计算域的进口,设置质量流量进口,进口流量设置为6 000 kg/s;取进水管出口作为计算域的出口,设置自由出流条件,参考压力为101.325 kPa;液面设为对称边界条件;其他壁面设置为Wall,采取标准壁面函数处理;采用一阶迎风格式,收敛精度为10-4.
1.4 网格无关性
在ANSYS Mesh中采用非结构化网格依次对前池和进水池进行网格离散.由于网格的数量和质量对数值计算结果影响很大,需对其开展无关性分析,为此剖分了8组网格,网格数量分别为15.1万,46.8万,81.4万,111.8万,183.1万,265.5万,345.1万和421.3万.
图2为网格划分示意图.图3为不同网格方案下的水力损失,当网格数量N超过183.1万时,水力损失Δh误差在±2%以内,因此采用该网格开展计算.

图2 网格划分示意图

图3 不同网格数量下的水力损失
将总水力损失作为特征参数,可采用式(3)利用进、出口的总压来计算总水力损失,即
(3)
式中:Δh为总水力损失;pin为进口处总压强,Pa;pout为出口处总压强,Pa;ρ为水的密度,取1.0×103kg/m3;g为重力加速度,取9.8 m/s2.
2 特征断面和流态评价指标
2.1 特征断面选取
图4为各方案整流措施,图中L1为进水池长度;L2为J型导流墩尾端距进水管中心线的距离;L3为J型导流墩直线段长度;L4为J型导流墩直线段与圆弧段间距;L5为J型导流墩圆弧段尾端直线段长度;L6为翼型导流板的弦长(最大长度);L7为翼型导流板的最大厚度;W1为进水池宽度;W2为J型导流墩直线段到进水池边壁的距离;W3为J型导流墩的宽度;R为J型导流墩圆弧段内圆半径;α为翼型导流板仰角(翼弦与水平面的夹角);β为J型导流墩圆弧段的角度;H1为下层翼型导流板距底板的高度;H2为中层翼型导流板与下层翼型导流板间距;H3为中层翼型导流板与上层翼型导流板间距;H4为上层翼型导流板距水面的高度.为了定性分析进水池面层、中层和底层流态,分别截取3个断面,如图4a所示.断面1-1靠近水面,距底板高度H=3.5D;断面2-2为中间断面,距底板高度H=2.5D;断面3-3靠近底板,距底板高度H=0.5D.为了定量分析吸水管前的流动状况,顺水流方向,在距吸水管中心线D处截取纵剖面4-4,如图4a所示.

图4 各方案整流措施
2.2 流态评价指标
对于纵剖面4-4,采用进水流道水力性能评判的目标函数,即轴向速度分布均匀度vau、速度加权平均角θ以及断面平均轴向速度va进行定量分析.轴向速度分布均匀度vau用于判别特征断面上轴向流速的分布均匀程度,其数值越接近100%,断面流速分布越均匀;速度加权平均角θ用于表征断面轴向速度与断面的夹角,其数值越接近90°,流动平顺性越好[1].
3 整流措施几何特性
针对无措施时进水池内存在的不良流态,文中共设计了3种整流措施,分别为翼型导流板、J型导流墩以及翼型导流板+J型导流墩,如图4所示.翼型选用标准的NA012翼型,各整流措施的尺寸见表1,其中,各整流措施中导流墩的高度与水深相等.
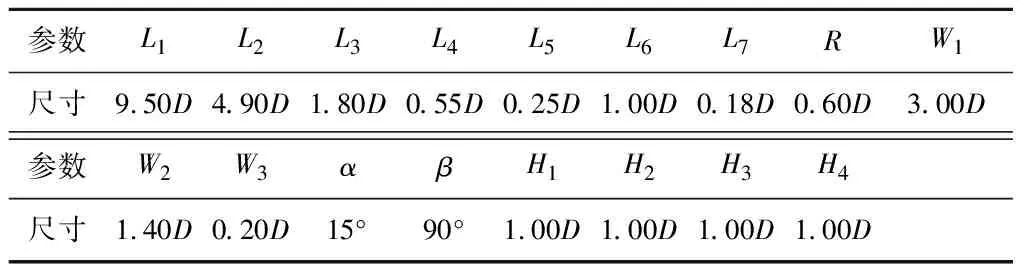
表1 各整流措施位置及尺寸
4 计算结果分析
4.1 横断面流态分析
图5为各方案进水池面层的流线分布及速度v云图.从图5a可以看出,原方案下1#—3#进水池流态紊乱,尤其是进水池左侧存在大尺度的回旋区(图中红色虚线),其中3#进水池后壁处存在水流回旋,2#和4#进水池后壁池可能形成水流回旋.
针对原方案进水池内流态紊乱,方案1在进水池进口处设置翼型导流板,可以破坏立面水流回旋,使得进水池流态得到很大改善,从图5b可以看出,相比原方案,1#进水池大回旋明显变小,2#和3#进水池大回旋区消失,仅在进水池后壁处形成很小的水流回旋.方案2在进水池进口处设置J型导流墩,其弧形部分切合侧向进水水流,使水流流态更加均匀对称.从图5c可以看出,相比原方案,1#进水池大回旋明显变小,2#和3#进水池大回旋区消失,进水池水流均匀对称,仅在进水池后壁处形成很小的水流回旋.为了进一步改善进水池流态,方案3采用联合措施“J型导流墩+翼型导流板”,从图5d可以看到,进水池大回流消失,仅在后壁出现轻微的水流回旋,进水池整体水流流态均匀对称.图6为各方案中层的流线分布及速度云图.
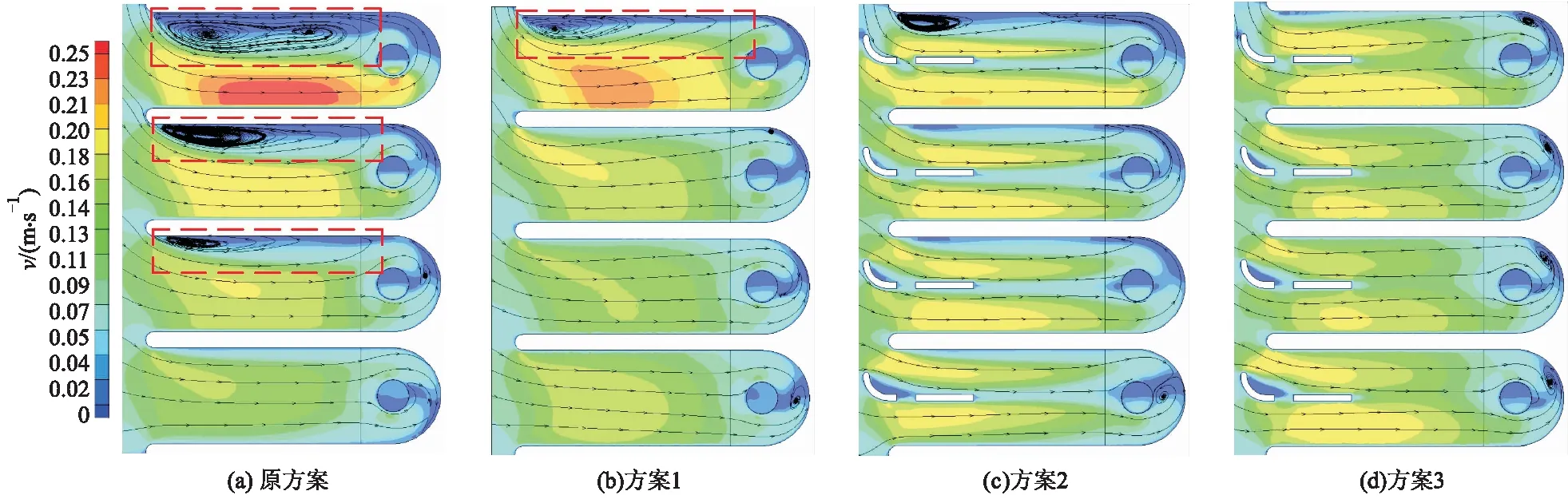
图5 各方案面层流线分布

图6 各方案中层流线分布
从图6a可以看出,原方案下,1#—3#进水池左侧均存在大面积的回流区,顺前池主流方向进水池回流区逐渐变小,其中3#进水池后壁有水流回旋.从图6b可以看出,经方案1整流后,1#进水池回流区明显减少一半,2#和3#进水池回流区消失,其中4#进水池后壁处有水流回旋.从图6c可以看出,经方案2整流后,1#进水池回流区大面积减少,2#和3#进水池回流区消失,其中4#进水池后壁处有水流回旋.从图6d可以看出,经方案3整流后,相比其他方案,进水池左侧大回流消失,流态均匀对称,仅在进水池后壁处出现水流回旋,整体流态好.
图7为各方案底层的流线分布及速度云图.从图7a可以看出,原方案中1#和2#进水池左侧均存在回流,3#和4#进水池流线平顺.从图7b可以看出,经方案1整流后,1#进水池流态有所改善,2#进水池回流区消失.从图7c可以看出,经方案2整流后,1#进水池回流区明显减少一半,2#进水池回流区消失.从图7d可以看出,经方案3整流后,相比其他方案,1#进水池流态有所改善,整体流态均匀对称.

图7 各方案底层流线分布
4.2 纵剖面流态分析
为了更好地分析各方案的整流效果,计算了各方案下进水池纵剖面的轴向流速分布均匀度、速度加权平均角和断面平均轴向流速,计算结果如表2所示.由表2可以得知:① 各方案进水池纵剖面轴向流速分布均匀度随进水池距前池进口距离的增加整体呈上升趋势,原方案轴向流速分布均匀度上升趋势较缓,其中1#进水池为73.17%,方案1轴向流速分布均匀度上升趋势明显,与原方案相比,4#进水池提高了10.31%.方案2轴向流速分布均匀度上升趋势较原方案更为平缓,与原方案相比,2#进水池下降了5.51%.方案3轴向流速分布均匀度上升趋势最为明显,相比原方案,4#进水池提高了12.20%,因此方案3整流效果最好.② 原方案及方案2速度加权平均角与进水池距前池进口距离呈负相关关系,与原方案相比,方案2下降趋势更加平缓,其中3#进水池相比原方案提高了0.2°,方案1及方案3速度加权平均角与进水池距前池进口距离并非单调变化关系,各方案3#进水池均为最优,其中方案3数值最大,因此方案3整流效果亦最好.③ 原方案、方案2及方案3进水池断面平均轴向流速随进水池距前池进口距离的增加单调递减,其中,原方案各进水池断面平均轴向流速下降趋势最为明显,最大差值为0.059 m/s.方案2断面平均轴向流速下降趋势较缓,最大差值为0.019 m/s,方案3下断面平均轴向流速更为平缓,最大差值仅为0.001 m/s,可忽略不计.但与其他方案相比,方案1变化趋势不同,亦非单调变化关系,其中,2#进水池断面平均轴向流速最小,综合分析后,方案3整流效果最好.

表2 各方案纵剖面流态评价指标
图8为各方案下进水池纵剖面轴向速度w云图(从左至右依次为1#—4#进水池).从图8a可以看出,原方案下各进水池纵剖面流态分布极度不均,且1#—3#进水池左侧均存在负流速区,高速区均在右侧;从图8b可以看出,方案1下各进水池纵剖面流态分布有所提高,其中2#和3#进水池负流速区消失,1#进水池回流区明显变小,高速区基本在进水池中间;从图8c可以看出,方案2下各进水池纵剖面流态分布均匀,其中1#—3#进水池回流区大面积减少,高速区基本在进水池中间;从图8d可以看出,方案3下各进水池纵剖面流态分布基本均匀,各进水池回流区消失,高速区在进水池中间.因此方案3整流效果最佳.
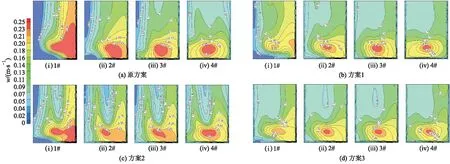
图8 各方案进水池纵剖面轴向速度云图
通过对比不同方案进水池纵剖面轴向流速分布均匀度、速度加权平均角、断面平均轴向流速和轴向速度云图可发现,方案3下进水池流态最好.
5 结 论
针对侧向进水泵站进水池出现的大尺度回旋问题,提出了在进水池加设J型导流墩、翼型导流板以及J型导流墩+翼型导流板的整流措施,分别分析了3种整流措施对进水池的改善作用,得出如下结论:
1)原方案进水池均存在大尺度的回旋区,大回流区由进水池进口延伸至进水管前端,流态分布极度不均匀.
2)3种整流措施均可有效改善进水池流态,进水池大尺度回旋基本消失.J型导流墩的弧形部分很好地切合侧向进水主流方向,并结合直线部分对水流有很好的导向作用;翼型导流板可以破坏水流回旋,并对水流有很好的平顺作用.所选的J型导流墩+翼型导流板方案进水池纵断面轴向流速分布均匀度整体大于其他方案,轴向流速分布均匀度可提高12.2%.
3)提出的3种整流措施均是在原有基础上开展的创新性设计,结果和机理分析表明整流效果良好.研究成果不仅丰富了相关理论,拓展了整流措施的选择,还可用于其他同类小型泵站,应用前景巨大.

