一种兴趣驱动的跨网络传播优化算法

李 雷 邓诗琦 赵 博 施化吉 施磊磊

1(江苏大学计算机科学与通信工程学院 江苏 镇江 212013) 2(中国传媒大学新闻传播学部新闻学院 北京 100024)

0 引 言

社交网络的开放性、便利性及内容的丰富性吸引了广大的用户人群，同时也为在线推荐系统和病毒式营销提供了良好的平台。近年来，基于社交网络的精准广告投放已经成为首要选择。其中，影响力最大化问题以“口碑营销”为基础对用户影响规则及影响力传播模式进行研究，具有重大的理论意义和实用价值。

文献[1]给出了影响力最大化问题的相关研究进展。Domingos等[2]首先将影响力最大化问题引入社会网络领域，并给出了该问题的详细定义与评价指标。Kempe等[3]在此基础上将影响力最大化形式化定义为在特定影响力传播模型中挖掘影响力大的k个节点的离散优化问题，并证明了影响力最大化问题是一个NP-hard问题，且用贪心算法可以得到精确度为(1-1/e)的近似最优解，但其时间复杂度高、效率低下。针对此问题，一些研究者对影响力最大化问题的贪心算法作出了一系列改进[4-6]，也有研究者提出用启发式算法[7-10]解决该问题。除了提升算法的运行效率外，很多研究以提升问题模型的实用性为目标进行开展，如通过考虑主题感知这一因素以提升影响力传播模型的准确性[11-12]；将挖掘全局影响力最大的节点具体化为挖掘某一特定地理位置内影响力最大的节点[13-14]；将成本因素引入影响力最大化问题[15-16]等。

上述研究都是基于单网络对影响力最大化问题进行了较为充分的研究，然而随着用户的跨网络参与行为逐渐增多，各社交网络间的交集也随之增加，学者开始从跨网络的角度探究影响力最大化问题。Shen等[17]利用“兴趣匹配用户”研究了信息的跨网络传播模式，通过将重叠用户表示为一个超级节点的方式耦合多个网络，然而这种方式无法体现用户在不同网络中的特性。Nguyen等[18]首次在病毒式营销的背景下引入跨网络影响力最大化的概念，并提出一种完全保留原始网络影响传播特性的耦合方案。随后，文献[19]进一步提出无损和有损两种耦合方案，前者保留原始网络的所有属性以获得高质量的解，后者则专注于时间和内存消耗，同时提出一种可扩展的贪心算法解决多社交网络上最小花费的影响力最大化问题。李小康等[20]证明了多渠道的影响力最大化问题在独立级联模型下是NP-hard问题，并针对该问题提出了贪心算法、基于节点度、基于反向可达集三种近似解决方案。但该研究是针对特定用户集开展的，即多个网络中的节点是相同的，这种特定情况下的算法和实验都具有一定局限性。李国良等[21]定义了不同网络中同一实体的自传播特性，并提出了影响计算模型解决多网络上节点间的影响概率，最后基于独立级联模型解决了多网络下的影响力最大化问题，算法的伸缩性较好。

然而，现有跨网络影响力最大化问题的解决方法[17-21]存在以下两个问题：(1) 过多关注多网络的耦合方式，忽略了网络中如主题偏好和交互偏好等用户兴趣特质对于影响力传播的影响。文献[22]指出，用户对自己感兴趣的领域的信息接受度大，将一个游戏广告推广给一个不玩游戏的用户，其接受广告并继续传播广告的可能性很低；反之，用户更加关注自己感兴趣的人，其从关注人群中获取的影响比从其他渠道获取的更大。因此，社交网络中影响力的传播是由兴趣驱动的，充分利用用户兴趣倾向能够更加精准地模拟信息在网络中的传播过程。(2) 现有方法没有很好地解决跨网络影响力最大化问题面临的随网络规模增加产生的计算负担。

为此，本文首先构建出同一跨网络用户之间的虚拟连接，以此作为媒介形成耦合网络；其次基于独立级联模型提出了兴趣驱动的跨网络影响力传播模型(ID-IPM)，以模拟信息在网络内部和网络之间的传播方式；最后针对随着网络规模扩大而增大的时间开销问题，提出启发式和贪心算法结合的优化种子节点选取方法(OA-IPaN)以解决跨网络影响力传播问题。本文主要工作如下：

1) 提出了一种兴趣驱动的跨网络影响力传播模型ID-IPM。首先，通过跨网络用户的“桥梁”作用进行网络耦合；其次，对独立级联模型进行了改进。该模型不仅通过跨网络用户的“桥梁”作用进行网络耦合，而且综合考虑跨网络用户在网络内部、网络之间进行信息传播的差异及用户兴趣的差异来计算节点间影响概率，以提高用户影响力的传播范围。

2) 基于ID-IPM模型，提出了一种启发式算法和贪心算法结合的跨网络影响力传播的优化算法(OA-IPaN)。该算法基于ID-IPM模型，利用启发式算法及贪心算法分两阶段进行种子节点的挖掘，以提高OA-IPaN算法的效率。

3) 实验结果表明本文提出的ID-IPM模型与OA-IPaN算法在影响范围和时间效率上的有效性，也验证了跨网络环境中挖掘种子节点相比单网络环境中的高效性。

1 相关工作

影响力最大化是以病毒式营销为背景、信息传播模型为基础的种子节点选择问题，被广泛应用于广告投放、谣言预警等领域，已成为社交网络分析中的研究热点。然而现有的大部分研究通常应用于某个特定社交网络，只分析一个网络中的各类数据，导致用户的影响力评估准确率低、影响范围窄。

单一网络中的影响力最大化问题自提出以来其解决方法已经被学者做了较为充分的探索。部分学者考虑到利用社交网络的社区结构性质能够降低问题的处理规模从而节省时间开销，例如：Wang等[26]提出的CGA先把网络分成多个社区再采取动态规划算法计算每轮应该选择种子节点所在的社区，最后再利用MixGreedy算法在该社区里寻找种子节点。有学者从网络发布内容出发解决问题，例如：Barbieri等[11]通过主题建模研究社交影响力，并基于传统的IC模型和LT模型提出了能够更准确模拟现实世界信息扩散的话题感知模型TIC和TLT；Chen等[12]在此基础上研究了主题感知下的影响力最大化问题；Li等[13]首次从地理位置的角度出发进行研究，旨在从某一给定地理区域中找到k个能够将影响力在此区域中传播到最大范围的种子节点，此后文献[14，27-28]也做了更深入的研究。除此之外，有学者从时间感知[29-31]、动态[32-33]和竞争性[34-36]等方向对影响力最大化问题进行了研究。总之，单一网络中的影响力最大化问题已经从多角度多方位得到了较为充分的研究，而随着许多用户的跨社交网络平台参与行为逐渐增多，各个社交网络间的交集也随之增加，学者开始从跨网络的角度探究影响力最大化。

从文献[37-38]开始，学者开始探索多个网络中的信息传播模式。文献[37]利用SIR模型(Susceptible Infected Recovered Model)模拟了信息在随机网络里的扩散形式，其首次研究了不相连节点在多个网络里的性质，为进一步研究信息以及影响力在多个网络中的扩散提供了线索。文献[38]提出了一种基于事件的社交网络，将线上的虚拟社交网络与线下的真实社交网络相连，并实现了该网络里的信息流模拟与社区发现。此后Nguyen等[18]首次在病毒式营销的背景下引入了跨网络影响力最大化的概念，并提出了一种完全保留原始网络影响传播特性的耦合方案，利用线性阈值模型让种子节点在多个网络里交叉传播影响力以达到将影响力在多个网络里扩散到最广范围的目的。为了进一步缩减选择种子节点产生的开销，文献[19]为跨网络影响力最大化问题设定了预算的限制，并进一步提出无损和有损两种网络耦合方案，前者保留原始网络的所有属性以获得高质量的解，后者则专注于时间和内存消耗，同时提出了一种可扩展的贪心算法，在保证最小开销的前提下完成了影响力最大化在多个网络中的求解。Zhan等[39]将同时在多个网络中拥有账号的重叠用户定义为锚用户，锚用户各个账号之间的链接定义为锚链接，拥有锚用户的多个社交网络定义为部分匹配的在线社交网络(Partially Aligned Social Networks)，从部分匹配的在线社交网络中挖掘种子节点，并定义了网间和网内两种路径来模拟信息的跨网络传播。除此之外也有一部分学者基于IC模型来求解跨网络影响力最大化，文献[20]证明了IC模型中的多渠道影响力最大化为NP-hard问题，并针对该问题提出了贪心算法、基于节点度、基于反向可达集三种近似解决方案。为了解决跨网络影响力最大化问题，文献[21]考虑了不同网络间同一实体的自传播特性，利用一种特定的模型计算多个网络中节点间的影响概率，然后基于IC模型提出了多个优化方法。针对目前绝大多数研究跨网络影响力最大化的算法均从网络的拓扑结构出发，没有充分考虑到网络中用户的特殊属性的情况，Shen等[17]利用“兴趣匹配用户”研究了信息的跨网络传播模式，通过在真实社交网络Twitter-Foursquare和学术合作网络上的实验，证明了其算法的有效性。

跨网络影响力最大化是单网络影响力最大化的扩展，即在给定的多个社交网络中挖掘出一群用户，让它们在这些社交网络的整体范围内影响尽可能多的用户，其中这些网络内部的用户会在各个网络内部传播信息，且跨网络用户会在网络间交叉传播信息。可见跨网络影响力最大化的研究需要以网络之间的信息交流为基础，且跨网络用户是不同网络间的连接媒介。

2 问题描述与相关定义

跨网络影响力最大化问题的目标是从n(n>1,n∈N*)个社交网络中寻找一个能将影响力传播到最广范围的种子节点集，其问题描述与相关定义如下。

不失一般性，本文工作在n=2个社交网络G1(V1,E1)和G2(V2,E2)上展开，其中Vi(i=1,2)和Ei(i=1,2)分别是网络Gi(i=1,2)的节点集合和节点间连接的集合。

定义1跨网络用户/非跨网络用户。同时在网络G1和G2中拥有账号的用户称为跨网络用户，反之只在其中一个网络中拥有账号的用户称为非跨网络用户。

相应地，在社交网络拓扑图中，跨网络用户对应的节点称为跨网络节点，非跨网络用户对应的节点称为非跨网络节点。

定义2现实个体。现实个体是社交网络中的账号在现实世界中对应的、可以相互区分的个体。

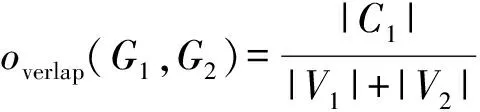
定义4种子节点集S。种子节点作为影响力传播的起点，是最初被激活的并尝试以自身影响力激活其邻居的节点。由种子节点组成的集合称为种子节点集，记作S。

定义5影响范围σ(S)。根据给定影响力传播模型，所有种子节点u∈S直接或者间接激活的现实个体集合用σ(S)表示。

本文利用被激活的现实个体而非被激活的节点来定义影响范围，原因是跨网络环境下被激活的节点中可能包含较多的跨网络用户，而影响传播的效果最终是作用在某一现实个体上的，若利用被激活的节点数量来量化影响范围的大小会导致影响范围的重复计算，从而使得影响传播范围判定过高。

3 兴趣驱动的跨网络传播模型

3.1 基于跨网络节点的重叠网络耦合策略

耦合重叠网络的关键是结合现实背景理解信息跨网络传播的具体方式。如图1所示，给定一对重叠网络G1(V1,E1)和G2(V2,E2)，其中节点a∈C1⊆V1和b∈C2⊆V2是一对跨网络节点，它们从各自参与的网络中接收到信息后会以一定的概率将该信息传播到另一个网络中。利用这一特性，ID-IPM模型在保留两个网络中全部结构特征的基础上，抽象出每一对跨网络节点之间信息传递的虚拟通道，从而将G1和G2耦合成耦合网络G。本文将该信息虚拟通道定义为跨网连边，具体定义见定义7。

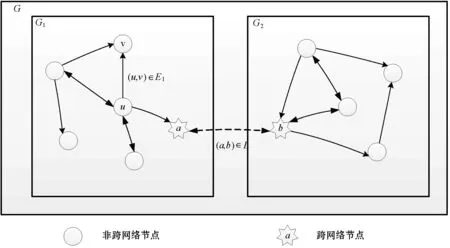
图1 重叠网络耦合策略图示

定义7跨网连边集L。一对跨网络节点之间的虚拟信息传播通道称为跨网连边，所有跨网连边组成的集合为跨网连边集，记作L。

例如图1中跨网络节点a和b之间的跨网连边(a,b)∈L就是网络G1和G2之间信息传播的一条虚拟通道。在构建网络G1和G2间的跨网连边后，信息可以在两个网络内部独立传播还可以通过跨网络节点进行传播，从而实现了重叠网络G1和G2的耦合。耦合网络的具体定义如定义8。

定义8耦合网络G。保留一对重叠网络G1和G2各自内部的全部节点和节点连接，并构建同一跨网络节点之间的虚拟跨网连边，得到耦合网络G(G1,G2,L)，其中L为G1和G2之间的跨网连边集。

3.2 兴趣驱动的节点间影响概率

构建出耦合网络G后，ID-IPM模型需要定义网络G中节点u∈V1∪V2之间的影响概率。用户受到和自己兴趣相似的用户的影响力更大，主题相似度和交互频度是描述用户兴趣相似的重要因素，因此ID-IPM模型依靠用户兴趣驱动——综合考虑主题相似度和交互频度定义网络内部节点之间的影响概率大小。

1) 主题相似度。用户主题偏好是用户兴趣特质在社交网络中的表现形式之一，两个用户关注内容的主题越相似，他们的兴趣就越一致，受到彼此影响的概率越高。本文通过对用户发布的文本信息进行LDA[23]建模得到用户关注的主题及相应的频度，再利用主题分布来表示用户的主题偏好，最后通过计算主题分布的相似度来表示主题相似度。

定义9主题相似度Φuv。假设u和v是同一网络内的节点，则这一对网内节点之间的主题相似度Φuv是两者的主题分布相似程度。

Φuv=1-DJS(Tu,Tv)u,v∈V1或u,v∈V2

(1)

式中：Tu和Tv为节点u和v的主题分布；DJS(Tu,Tv)为两个分布的JS散度。

2) 交互频度。由于网络内部的节点之间依靠关注、转发和评论等方式进行交互[24]，交互频度能够体现出用户的兴趣特质，交互越频繁影响力传播的可能性越高，其具体定义见定义10。

定义10交互频度Ψuv。同一网络内的节点u和v的交互频度Ψuv定义为两者之间转发消息的频率，其计算公式如下：

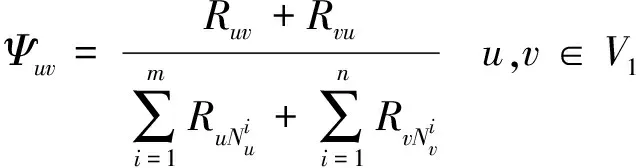
(2)

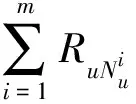
3) 节点间的影响概率。本文以兴趣为驱动综合考虑网内节点间的主题相似度和交互频度以判断影响概率的大小，并如定义11对网内节点间的影响概率进行定义。

定义11节点影响概率Puv。同一网络内部的节点u对v的影响概率Puv定义如下：

Puv=αΦuv+(1-α)Ψuv

u,v∈V1或u,v∈V2

(3)

由于主题相似度和交互频度具有同等的重要性，因此本文将调和因子α取值为0.5。

3.3 ID-IPM模型的影响力传播过程

ID-IPM模型是独立级联模型在跨网络环境中的应用和改进，该模型的影响力传播示例图如图2所示。

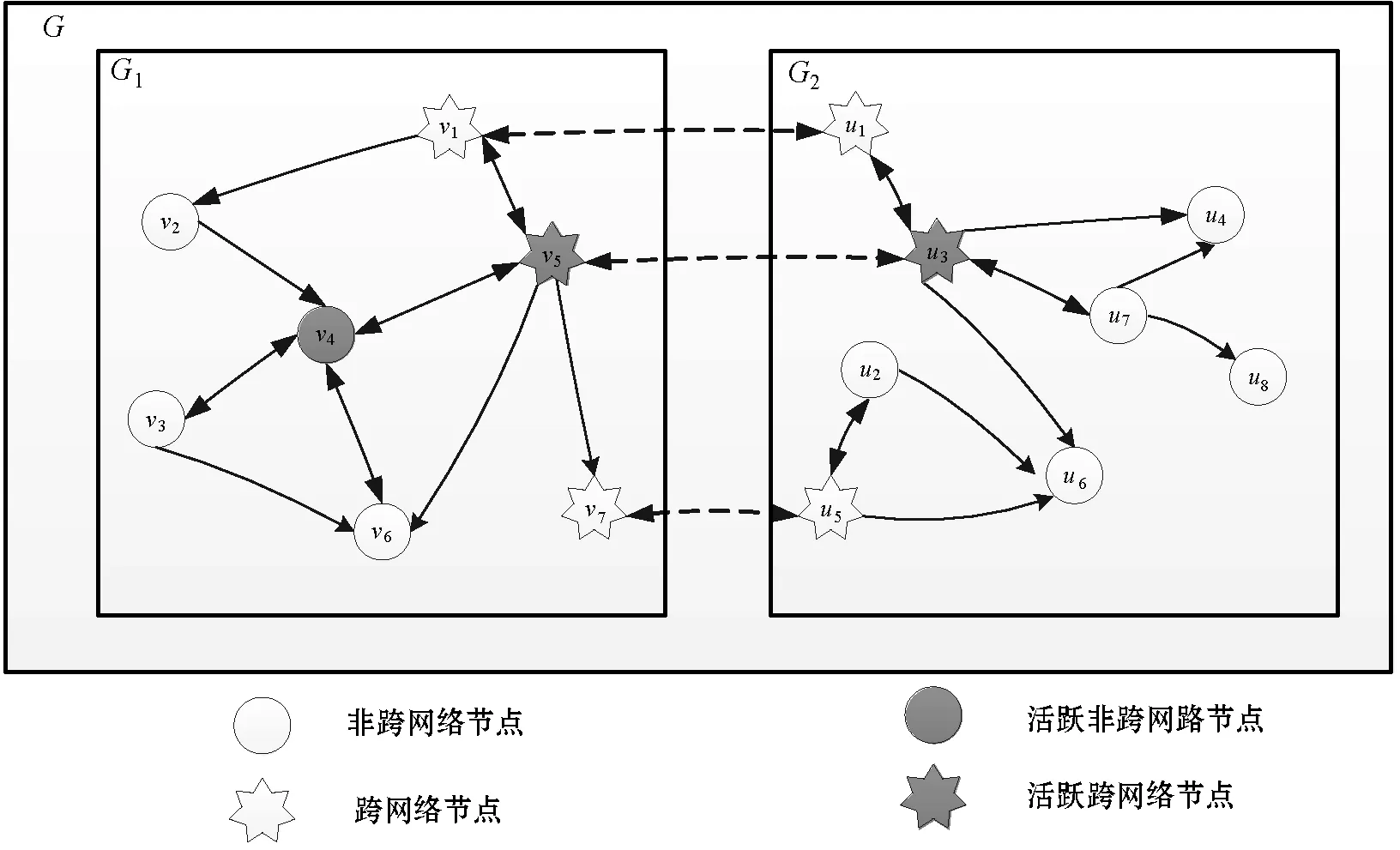
图2 ID-IPM模型影响力传播示例图

耦合网络G(G1,G2,L)中的影响力传播包括在G1和G2内部传播和在两者之间跨网络传播两部分。每个种子节点u∈S都以一定的概率去尝试激活其相邻的未激活节点，每一时刻产生的新激活节点会在下一时刻以同样的方式参与影响传播，如果G中没有新节点被激活或达到设置的阈值时传播过程终止。

图2中，v4∈V1、v5∈V1和u3∈V2为t时刻的激活节点，其中v5和u3为一对跨网络节点。这三个节点会对各自的出邻居节点施加影响力，如节点v4分别以概率pv4v3和pv4v6尝试激活G1内的未激活节点v3和v6，同理节点v5和u3以一定概率尝试激活G1内的节点v1、v6、v7及G2内的节点u1、u4、u6和u7。若节点u7被节点u3成功激活则会在t+1时刻分别以概率pu7u4和pu7u8去尝试激活节点u4和u8。若跨网络节点v7与节点u5是同一个节点，当其中一个被其他节点激活时，另一个就自动被激活，然后就能够将信息跨网络传递给其他节点，此为一次跨网络信息传播的过程。

ID-IPM模型中的激活行为只会执行一次。如图2中，由于节点u8只能接收到节点u7的影响力，一旦它未能被u7成功激活则它在该影响力传播过程中只能一直保持未激活状态。反之，节点u4能够接收到u3和u7两个节点的影响力，一旦它被两者中的任何一个成功激活都能转换为激活状态。

4 跨网络的影响力优化算法

针对IMaN问题，本文提出跨网络影响力传播优化算法(OA-IPaN)。兼顾时间开销和算法精度，将OA-IPaN算法分为以下两个阶段：1) 筛选候选节点集，利用节点的度中心性[25]初步筛选出能显著扩散影响力的候选节点集S0(|S0|=k0，k0>k)；2) 选取种子节点集，通过ID-IPM模型模拟候选节点的影响力传播情况从候选种子集合S0中筛选出种子集合S(|S|=k)。

该算法输入为耦合网络G，种子节点数k，比例参数p=k0/n(n=|V1|+|V2|,p∈(0,1])；输出为种子节点集S。

4.1 候选节点筛选

OA-IPaN算法在筛选阶段筛选出潜在影响力最大的候选节点集S0(|S0|=k0，k0>k)，通过忽略潜在边际影响力增量较小的节点来减少节点边际影响力增量的计算次数。综合考虑节点的度中心性[17]及跨网络节点的特性，潜在影响力PI的定义如下。

定义12潜在影响力PI。节点的潜在影响力PI表示其影响力传播能力的大小，u∈V1∪V2的潜在影响力PIu的计算如下：

(4)

式中：du表示节点u的出度；|V1|+|V2|-|C1|表示耦合网络G中能被影响的全部现实个体数。

算法1候选节点筛选

1.初始化候选节点集合S0=∅，并将耦合网络G中所有的状态标签标记为Selected=0；

2.根据式(4)计算耦合网络G中全部节点的潜在影响力PI，并按照PI值的大小进行排序；

3.选择PI值最大且状态标签为Selected=0的节点v作为候选节点并放入集合S0；

4.如果|S0|≥p×n，转到第6步，否则转到第5步；

5.判断v是否为跨网络节点：若v是跨网络节点，则将v的状态标签设置为Selected=1，转到第3步；否则将v及其对应跨网络节点u的状态标签均设置为Selected=1，转到第3步；

6.输出候选节点集S0。

4.2 种子节点集选取

OA-IPaN算法选取阶段通过ID-IPM模型模拟影响力传播过程，并利用子模优化[9]的贪心策略选择影响力增量大的节点得到种子节点集S(|S|=k)。其中向集合S中加入某一节点u影响范围的变化为影响力增量Δσ(u|S)，其具体定义见定义13。

定义13影响力增量Δσ(u|S)。若当前种子节点集S经模拟影响扩散后的影响范围为σ(u|S)，则加入节点u后增加的新激活现实个体集合即为影响力增量Δσ(u|S)，其计算方法如下：

Δσ(u|S)=σ(S∪{u})-σ(S)u∈S0S

(5)

算法2种子节点集选取

1.初始化种子节点集合，并设置t=1；

2.根据式(5)计算节点u∈S0S在t轮的影响力增量Δσ(u|S)并按照结果从大到小排序；

3.选出t轮有最大影响力增量Δσ(v1|S)=maxΔσ(u|S)的节点v1放入S，然后把v1从S0中移除；

4.若|S|≥k，则转到第16步，否则执行第11步；

5.将此时S0中影响力增量次大的节点v3记录为BaseNode，并将v3在t轮的影响力增量记录为BaseValue=Δσ(v3|S)；

6.令t=t+1；

7.计算此时S0中在t-1轮影响力增量最大的节点v2在第t轮的影响力增量Δσ(v2|S)，若Δσ(v2|S)≥BaseValue，转到第8步，否则转到第9步；

8.将v2放入集合S并从S0中移除，转到第4步；

9.按照第t-1轮的影响力增量排序依次计算除v2以外的其他节点在第t轮的影响力增量Δσ(u|S)，其中u∈S0S，转到第3步；

10.输出种子节点集S，算法结束。

4.3 算法复杂度分析

耦合网络G包含社交网络G1(V1,E1,C1)和G2(V2,E2,C2)，因此G中节点总数为n=|V1|+|V2|，连接总数为l=|E1|+|E2|+|L|，则OA-IPaN算法的时间复杂度分析如下：

(1) 计算耦合网络中所有节点的潜在影响力PI的时间复杂度为O(l)；(2) 启发式阶段筛选k0个候选节点的时间复杂度为O(pnl)；(3) 贪心阶段从候选节点集S0中挑选k个种子节点的时间复杂度为O(kRpnl)，R是蒙特卡洛模拟次数。

5 实 验

5.1 实验数据集和实验环境

本文使用的实验数据集来自Facebook和Twitter两个社交网络，利用爬虫技术随机获取用户公开数据，并分析重叠用户信息确定跨两个社交网络的用户，除网络中的推文数据外，具体统计结果如表1所示。实验环境采用Windows 10操作系统，Intel CoreTM i7-7500U 2.9 GHz CPU处理器，8 GB内存，编程工具是Anaconda 2，采用Python语言编写代码和进行相关实验。

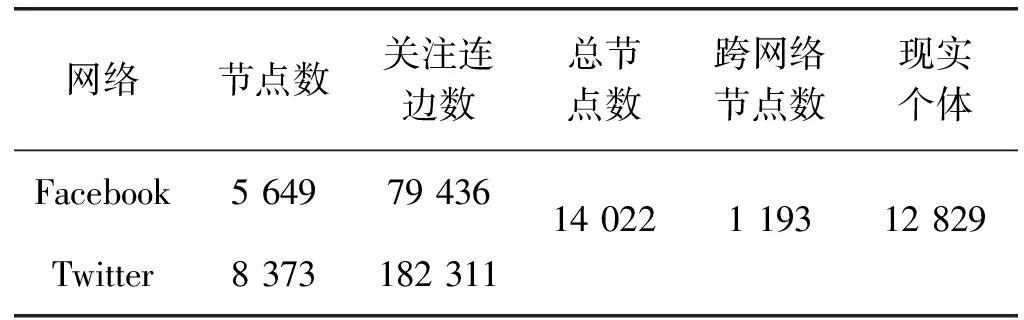
表1 从Facebook和Twitter获取的社交网络数据信息

5.2 实验结果与分析

影响力最大化旨在从网络中识别k个种子节点，使得通过这k个种子节点产生的影响传播范围最大。种子节点的选择是影响力最大化问题的核心，为此本文从以下四个方面对OA-IPaN算法的运行结果进行讨论：对比OA-IPaN算法与基准算法的影响范围和时间开销以验证算法性能；通过实验结果分析参数p设置对OA-IPaN算法的影响；分析种子节点的构成以及被激活节点的构成，从而说明跨网络节点对于影响力传播的重要性及不同网络信息传播能力的差异；通过对比实验验证跨网络影响力传播的优势。

5.2.1算法性能对比

为验证OA-IPaN算法在选择种子节点时的有效性，本文选择以下三种基准算法与之对比，其中OA-IPaN算法中的参数p设置为0.25。

(1) Greedy-IMaN：利用贪心算法从耦合网络中依次选取边际影响力高的节点作为种子节点，并采用ID-IPM模型进行影响力的模拟扩散。(2) Degree-IMaN：基于最大度启发式算法，其种子节点选取策略是从耦合网络中依次选取节点中出度最大的节点。(3) Random-IMaN：随机选择种子节点直到节点数量达到要求。

1) 算法影响范围对比。如图3所示，OA-IPaN算法与Greedy-IMaN算法得到的影响范围大小几乎一致，且始终优于另两种算法。OA-IPaN算法在k≤75时影响范围略低于Greedy-IMaN算法，随着k值增大在k=100时实现反超，并在k=175时又降到后者之下。这是因为OA-IPaN算法在筛选阶段筛选出潜在影响力PI较高的候选节点集，但是这种策略无法避免某些影响力高的节点被剥夺了选作种子节点的可能。当k较小时，OA-IPaN算法几乎能保证选出的候选节点即为真正影响力排名靠前的节点，而基本不会排除掉某些真正影响力高的节点，因此在k=175之前，OA-IPaN算法都能保持和Greedy-IMaN算法几乎一致的影响范围曲线。而随着k值不断增加达到某一数值(本实验中为k=175)后，算法无法保证候选节点是整个耦合网络中真正影响力最高的，因此OA-IPaN算法得到的影响范围逐渐减小直到低于Greedy-IMaN算法。然而在现实的病毒式营销中，一次广告投放的预算通常是有限的，种子节点的数目通常不会很大，因此在一定的预算内，OA-IPaN算法仍然能保证良好的效果。

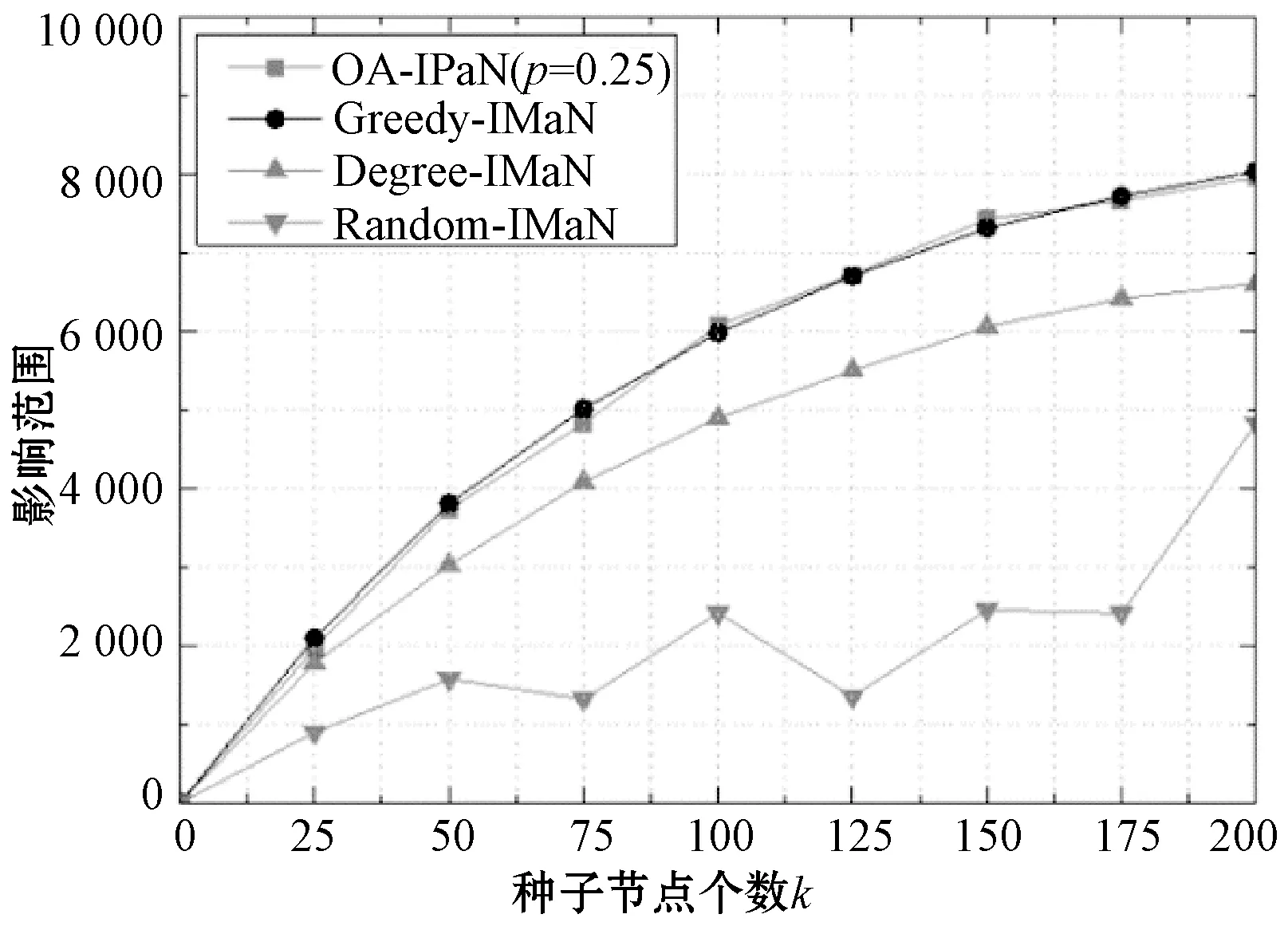
图3 影响范围的比较

另一方面，可以看出Degree-IMaN算法的影响范围曲线呈现持续上升的趋势，但远低于OA-IPaN算法和Greedy-IMaN算法。可见这种启发式算法虽然思想简单，却因为选择种子节点时没有进行影响力的模拟传播，使得无法避免被选择的节点之间存在大量影响力重叠的情况，从而导致影响力无法传播到较大的范围中。这也说明在跨网络影响力传播环境下，节点度的大小并不能直接代表其影响力的大小，直接利用节点的度选择种子节点得到的集合不一定能得到较好的影响力传播范围。此外，可以看出Random-IMaN算法取得的影响范围很小且其曲线呈现不规律的变化趋势，甚至在k值增加的过程中出现了下降的情况，原因是随机选择种子节点进行影响力传播的方式没有合理利用网络的拓扑结构和节点的性质。这种效果的不佳也侧面说明了利用影响力最大化算法选择影响力较大的种子节点进行影响力传播的作用是显著的。

2) 算法运行时间对比。为验证算法的时间效率，本文测试4种对比算法在耦合网络中挖掘出大小为k=50的种子节点集所需的时间，具体结果如表2所示。

表2 各算法运行时间对比表

可以看出，Degree-IMaN算法和Random-IMaN算法的时间效率很高，因为前者只需计算节点的出度再依次选择种子节点，后者的运行时间则取决于网络节点数n和种子节点数k的大小。节点的出度计算起来十分简单而n和k是事先给定的，因此这两种算法用时很短。Greedy-IMaN算法利用贪心策略选取种子节点，每选取一个种子节点就需要模拟一次影响力传播并重新计算各节点的影响力增量，耗时很长。在k=50时，Greedy-IMaN算法的运行时间已经达到了25 614 s，随着k值的继续增大，其运行时间长到难以应用到现实场景中。OA-IPaN算法采用两阶段方法挖掘种子节点，其中启发式阶段筛选出了潜在影响力较高的候选节点，后续贪心阶段仅需要从较小的候选节点集中挖掘种子节点，所以耗时仅为Greedy -IMaN算法耗时的1/7。Degree-ImaN和Random-ImaN算法尽管耗时更少，但影响范围小。

综上所述，OA-IPaN算法能在几乎和贪心算法保持一致的影响范围时显著减少运行时间，从而其有效性得以验证。

5.2.2参数p设置对算法性能的影响

候选节点集S0的大小k0由参数p=k0/n进行调节，参数p的选择对种子节点选择的结果、影响范围σ(S)的大小以及算法的运行效率都有着极大的影响，因此本文设置参数p从0.05开始以0.05为单位依次取值直到p=0.3，通过对比实验分析p值变化对算法的影响。

1) 参数p对算法影响范围的影响。由图4可知，当k取值较小时，p值的变化对算法影响范围的影响很小，这是由于影响力最高的节点几乎均被选为候选节点，极少高影响力的节点被遗漏，为贪心阶段挖掘出高质量节点提供了保证。而当k值增加到某一数值(本组对比实验中为k=100)时，p值对算法的影响逐渐变大。p值较小导致启发式阶段选出的候选节点集较小，其中难免排除一些影响力较高的节点，算法精度下降。

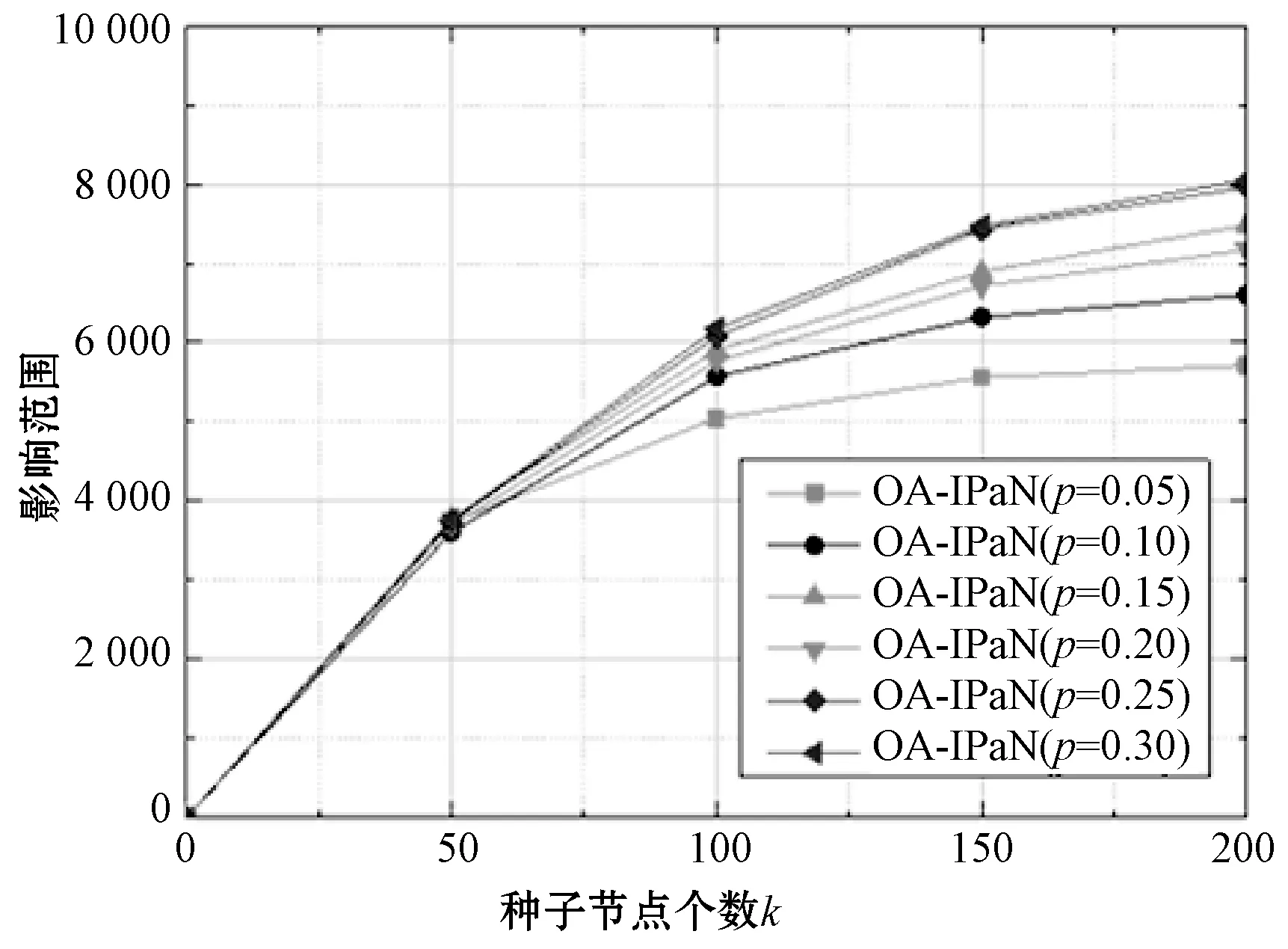
图4 参数p对影响范围的影响

2) 参数p对算法运行时间的影响。表3展示了k=50时不同p取值对算法运行时间的影响。可以看出随着p取值增加，算法运行时间变长，因为p越大候选节点集越大，贪心阶段需要计算边际影响力增量的节点数就越多，蒙特卡洛模拟的次数也越多。

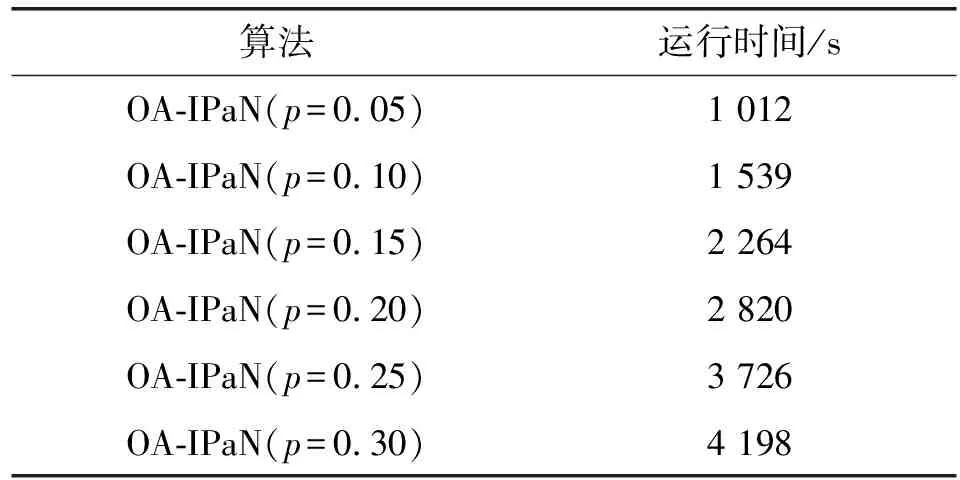
表3 p值对算法运行时间影响对比

在影响范围和时间效率之间找寻合理的平衡是算法的目标，在本数据集的实验中，从p=0.25开始，OA-IPaN算法的影响范围与Greedy-IMaN算法的结果相差无几，反而随着p值的继续增大，其运行时间大大增加，因此交叉对比实验结果可知当p=0.25时OA-IPaN算法的综合性能最好。

5.2.3种子节点集和激活节点集组成

本文通过实验分析种子节点集和最终被激活节点集的组成，从而分析两个网络对于影响力传播的贡献能力的差异。

1) 种子节点集组成分析。图5展示了p=0.25时OA-IPaN算法选择的种子节点集S的组成情况，即S中跨网络节点和非跨网络节点的比例随着种子节点数k的变化。图5中“Both”表示同时参与两个网络的节点，即跨网络节点，对应的“Twitter”和“Facebook”分别表示只参与这两个网络的非跨网络节点。

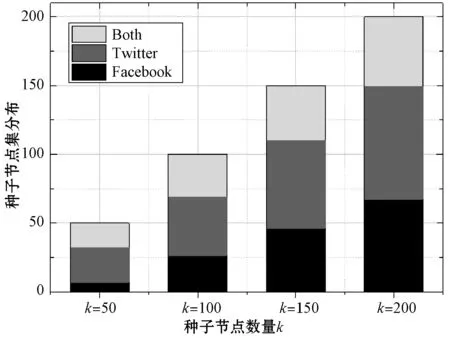
图5 种子节点集所属网络

(1) 两个网络中的非跨网络节点对比。由图5可知，无论k设置为多少，种子节点集S中来自Twitter网络的非跨网络节点的比例总是大于来自Facebook网络的节点，即Twitter网络对于种子节点的贡献率更高，均超过了37%，对应的Facebook网络的贡献率在k=200时达到最大值也仅为33.5%。这是因为本实验数据集中Twitter网络的规模明显大于Facebook网络，且Twitter网络中节点的度数普遍较高，所以选择Twitter网络中的节点作为种子节点能够取得较优的影响范围。

进一步分析可知，随着k值增大，Twitter网络对种子节点的贡献率逐渐降低，而Facebook网络的贡献率逐渐升高。原因是当k较小时，规模较大的Twitter网络中的节点比Facebook网络中的节点能为整个耦合网络提供更多的潜在可影响节点。当k增加到一定值时，Twitter网络中大部分节点已被激活，这时Facebook网络中的高影响力节点在耦合网络中反而能取得更好的影响效果，因此算法倾向于选择Facebook网络中的节点作为种子节点。

(2) 跨网络节点与非跨网络节点对比。从图5中可以看出，种子节点集S中跨网络节点占有较高的比例，在4组实验中其比例均大于25%，然而实验数据集中两个网络的重叠度仅有约8.5%。其中当k=50时种子节点中跨网络节点的比例最高，达到了36%，此后随着k值增加该比例略有下降，k=200时降为25.5%。跨网络节点在种子节点集S中的比例较高是因为它们能同时影响两个网络中各自的朋友，所以相比于只参与一个网络的用户节点拥有更广的潜在影响力传播范围，更容易被选为种子节点。k值较小时，跨网络节点对影响力传播的贡献很大，且k值越大贡献越小，这是由于当许多在两个网络中影响力都很大的跨网络节点已被选为种子节点后，影响范围已经在耦合网络中有了较大的扩散，此时两个网络中不参与跨网络传播的群体之间的影响力扩散对于整体的影响范围贡献更大，因此跨网络节点不再受青睐。

综上可知，合理利用跨网络节点的跨网络传播特性能有效减少种子节点的数量。

2) 激活节点集组成分析。图6展示了激活节点集的组成情况随k值变化的柱状图，即OA-IPaN算法选择的种子节点最终激活的所有节点在两个网络中的分布情况。图6中 “Both”表示被激活的跨网络节点，对应的“Twitter”和“Facebook”分别表示被激活的、只参与这两个网络的非跨网络节点。

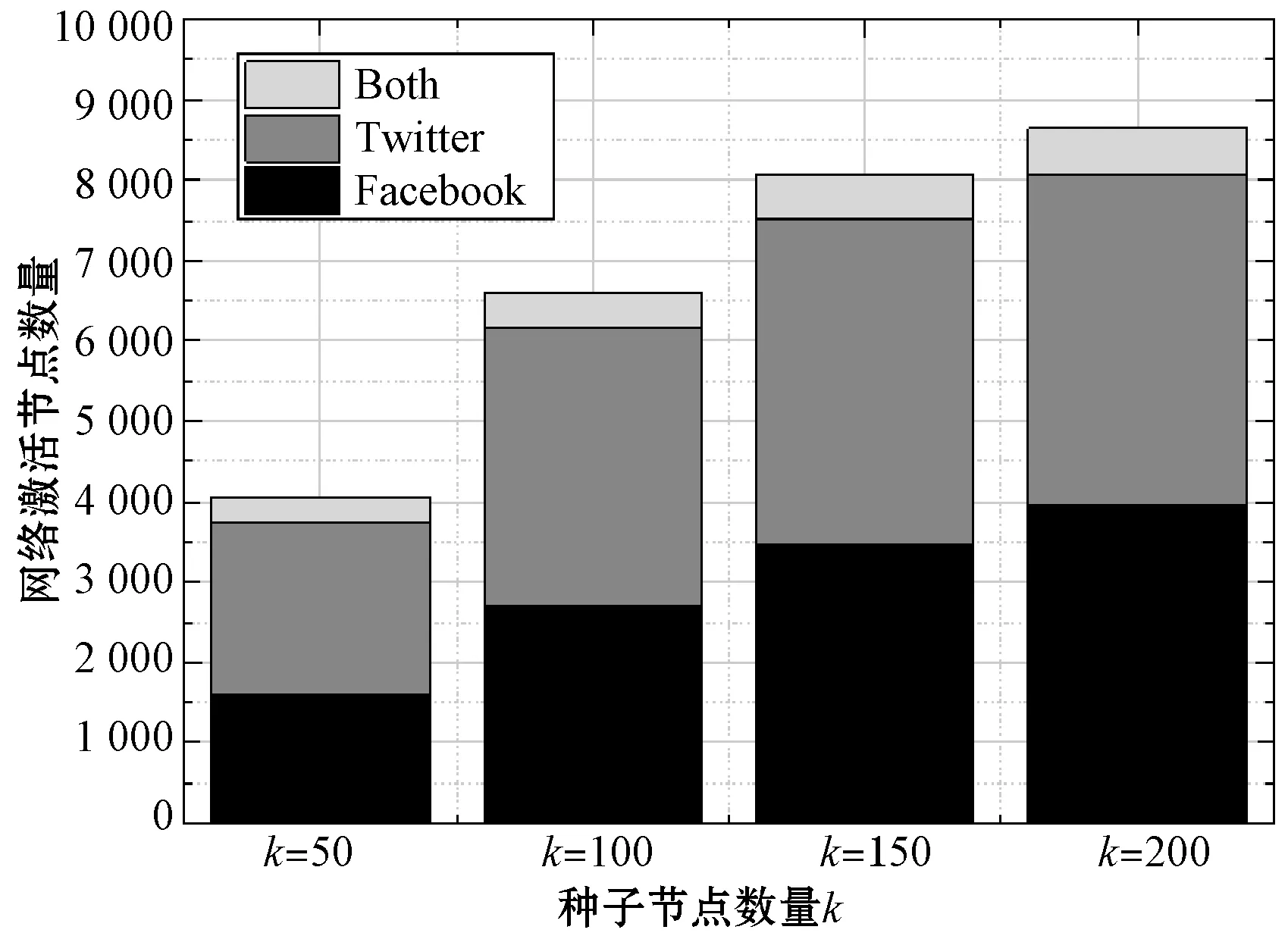
图6 激活节点集所属网络

在所有被激活节点中，跨网络节点所占的比例较小，在k=50时该比例最大也不到8%，随着种子节点集S增大被激活的跨网络节点的数目呈现出较缓的增长趋势，但占所有被激活节点的比例逐渐下降，在k=200时该比例降为6.7%。

若不考虑跨网络节点，单独分析被激活的非跨网络节点在两个网络中的分布可知，随着k值从50增加到200，最终被激活的非跨网络节点中属于Facebook网络的比例从39.5%提升到45.8%，反之被激活的非跨网络节点属于Twitter网络的比例略有下降，从52.4%下降到47.7%。这种现象与种子节点集S的组成情况相对应，k较小时来自Twitter网络的种子节点较多，因此最终激活的节点也大多来自Twitter网络，而随着k值的增大，算法更倾向于选取Facebook网络中的节点作为种子节点，所以属于Facebook的对应激活节点更多。

进一步分析可知两个网络中选出的种子节点数和最终被激活的节点数略不平衡。以k=50为例，被激活的节点约有52.4%的节点(不考虑跨网络节点)属于Twitter网络，然而结合图5可知k=50时来自Twitter的种子节点占总种子节点的63%；同理可知，k=50时有37%的种子节点属于Facebook网络，而最终Facebook网络中被激活的节点却占总被激活节点的约39.5%。显然种子节点数占比较小的网络激活的节点占比提升了，反之含种子节点多的网络未能按照同等的比例激活此网络内的节点。这种现象说明即使跨网络节点为两个网络提供了影响力传播的通道，但不同网络中的用户接受影响的能力是不同的，影响力在不同网络中的传播能力也是不一样的。

5.2.4跨网络影响力传播的优势

本文在不考虑时间效率的情况下比较了在耦合网络中与在多个独立网络中分别挖掘出的种子节点各自能将影响力传播到多大的范围。此组对比实验中影响范围都用最终被激活的节点数目来量化，其中三种对比算法描述如下。

(1) OA-IPaN(p=0.25)：本文算法采用ID-IPM模型模拟耦合网络中影响力的传播，并利用启发式和贪心策略两阶段选取种子节点，其中参数p取值为0.25。

(2) Twitter-IM：仅利用Twitter网络中内部的传播通道进行影响力传播，并利用贪心算法选择种子节点，其中影响力传播的模拟利用IC模型实现。

(3) Facebook-IM：与Twitter-IM类似，在Facebook网络中利用贪心算法挖掘种子节点并利用IC模型模拟影响力的传播方式。

图7展示了为达到同等规模的影响范围(即激活节点数)三个对比算法各需要的种子节点数目。可见对比另两种算法，本文OA-IPaN算法利用平均约1/5的节点数就能将影响力传播到两个网络的大量节点中，即OA-IPaN算法挖掘出的种子节点质量更高。此外，对比Twitter-IM 和Facebook-IM算法发现，在Facebook网络中想要达到同等规模的影响范围需要的种子节点数目更多，这是因为Facebook网络中节点数以及节点间连接数都很小，影响力在该网络中较难传播。

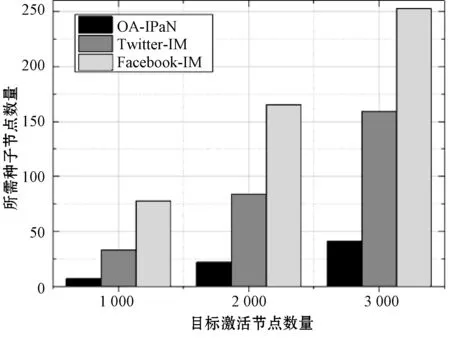
图7 相同规模影响范围所需种子节点数量

综上所述，合理利用跨网络节点的跨网络影响力传播特性进行影响力传播不仅能拥有更大的影响力传播空间，而且能以更高的效率取得更广的影响范围。

6 结 语

本文首先将多个网络耦合成一个网络再综合考虑跨网络节点的信息传播特性和用户的兴趣特质，提出了ID-IPM模型。其次，在ID-IPM模型基础上，提出了OA-IPaN算法分挖掘种子节点，其中在筛选阶段利用节点的度中心性初步筛选候选节点，减少了大量运行时间，在选取阶段根据子模特性优化的贪心算法进一步挖掘种子节点，提升了算法精度。实验结果说明了OA-IPaN算法在解决跨网络影响力最大化问题时在影响范围和时间效率上的有效性，并验证了跨网络挖掘种子节点相对单网络环境中的高效性。未来将通过增加网络个数从而在更大的网络环境中研究跨网络影响力最大化问题，以及尝试找寻其他的切入点，研究和设计出更加全面的、符合现实规律的影响力传播模型。