计及直流限额动态调整的送受端一体化日前调度计划模型

许 丹 周京阳 黄国栋

（中国电力科学研究院 北京 100192）

0 引言

我国具有一次能源与电力负荷逆向分布的特点，西南地区为水能富集区，西北及东北地区为风光资源富集区，而负荷中心则在中东部地区。近年来，在上述能源富集区已逐步形成了大规模水电、风电、光伏基地，与之相匹配的是特高压交直流输电的快速发展。清洁能源大容量跨省跨区外送已成为电网 运行常态。其中，复奉、宾金、锦苏三大直流将西南地区水电送往华东负荷中心，而祁邵、天中直流则将西北风电和光伏送到中部地区。虽然通过特高压直流输电可以直接将远端清洁能源经济地送至负荷中心，但是送受端的能源结构特性和网架结构却给这种能源输送模式在调度运行上带来了一定的挑战。对于送端，由于风光具有极强的随机性和不可控性，难以做到通过直流直接外送，因此规划设计中采用了风光火打捆外送的方式[1-2]，风电、光伏、火电及直流需要实现协调配合。对于受端，当交流网架不够健壮时，为了保证受端电网的安全稳定运行，受端电网的运行方式将限制直流的稳定限额，而无法充分发挥直流输电能力。

对于特高压直流外送问题，文献[3]提出了一种特高压直流外送风光火一体化调度计划模型，该模型能够灵活处理外送风光、配套火电、电力交易及直流计划的协调问题，但只能在固定已知的直流限额条件下求取，且无法精细化考虑受端电网的运行需求。文献[4-7]建立了考虑电网安全的风-火、风-水协调优化调度模型，但未包含送受端电网协调调度、直流运行等问题。安全约束机组组合（Security Constrained Unit Commitment, SCUC）和安全约束经济调度（Security Constrained Economic Dispatch, SCED）是调度计划编制和电力市场出清的基础技术[8-9]，当前SCUC研究通过模型描述改进[10-11]、新算法[12-13]、系统降维[14-16]和分解协调[17-19]等诸多办法在大规模模型构建和快速求解方面取得了较大突破。

实际运行中，对大规模电网进行调度运行时，需要考虑系统的频率、功角、电压等各类安全稳定问题。为了便于调度运行人员开展事前安全预控，提升对安全裕度的把控能力，电网调度部门会将涉及电网安全稳定的各类控制要求形成电网年度运行方式报告。报告通过对交直流输电断面有功限额、开机方式（开机台数、开机容量等）、正负备用容量等各类便于操作的决策量调整[20-21]实现安全稳定控制。由于机组组合结果可直接影响开机方式和正负备用容量，从而影响输电断面的功率限值，因此在某些情况下，将输电断面功率限额作为已知边界值构建安全约束机组组合模型时，只能以降低全局最优性为代价，采取保守的限值以规避方式调整所带来的安全风险。文献[21]已经关注到在计划编制过程中应该考虑配套电源开机台数对限额的影响，但是其仅针对送端开机台数与限额的关系，模型还应进一步完善。

本文以特高压直流风光火打捆外送实际问题为背景，针对直流计划与送受端电网计划耦合性较弱、不能动态考虑直流限额调整、送受端协调困难且无法充分发挥特高压直流的输电能力等问题，提出将送端的风光火打捆外送、直流输电及受端机组组合进行统一考虑，将开机台数、开机容量和备用容量等电网方式信息对直流限额的影响纳入机组组合模型，构建了计及直流限额动态调整的送受端一体化调度计划模型。模型可在保障电网安全的前提下，一次性求得配套火电、直流输电及受端机组计划，既可以确保全局最优性，又可以有效提升直流利用效率。

1 直流稳定限额简介

在受端电网不够健壮时，直流输电限额不仅需要考虑送端电网的安控装置、切机容量等因素，还受限于受端电网运行方式。电网运行方式由系统网架结构、负荷水平、机组开机、系统正负备用等多因素联合决定。电力调度部门根据不同的方式组合，分别计算直流稳定限额，以确保在限额范围内受端电网安全稳定运行。

特高压直流方式限额见表1。从表中数据可知：该条特高压直流输电线路的稳定限额受制于受端电网负荷水平、中部地区火电开机台数、负荷中心区火电开机台数及系统主网旋转正备用等多个因素影响。当需要提升特高压直流输电限额时，则需要增加受端电网的开机台数和主网旋转正备用容量，通常这种关系是单调正相关的。

表1 特高压直流方式限额Tab.1 UHVDC transmission limit

2 计及直流限额动态调整的送受端一体化调度计划模型

2.1 模型优化目标

所提模型的优化目标是在调度周期内使机组的开机费用、运行费用的总和最小，目标函数为

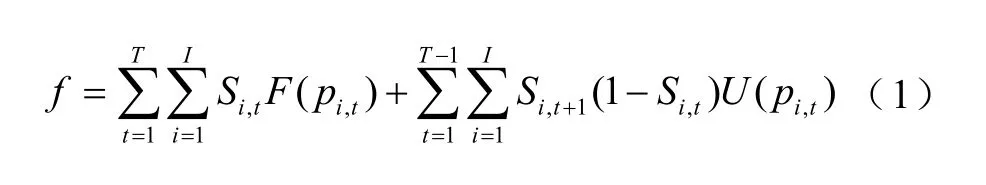
式中，T为规划周期内的总时段；I为机组总数；Si,t为机组i在时段t的状态，为决策变量（1表示开机，0表示停机）；pi,t为机组i在时段t的出力值，为决策变量；U(pi,t)为机组i在时段t的开机费用；F(pi,t)为机组i在时段t的运行费用。在优化目标中同时包含了送端和受端机组。

F(pi,t)费用通常采用二次函数描述为

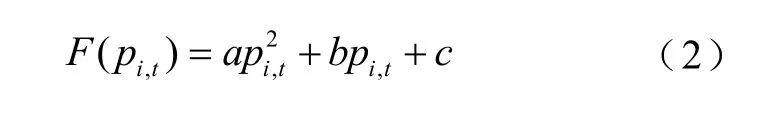
式中，a、b、c为二次函数的特性值，具体取值与机组的特性相关。

2.2 送端外送运行约束

通常特高压直流不仅需要输送配套电源的电能，还将输送送端电网的其他跨省区电力交易。因此直流功率平衡约束为

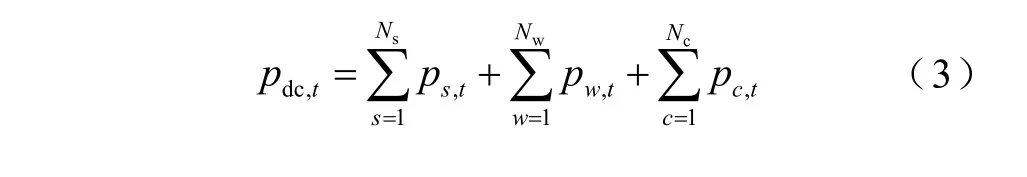
式中，pdc,t为直流在时刻t的外送计划；ps,t为送端配套火电s在时刻t的计划值；Ns为配套火电总数；pw,t为外送风光w的在时刻t的计划值；Nw为配套风光电厂总数；pc,t为送端省份电力交易分量c在时刻t的交易值；Nc为电力交易总数。

在消纳能力或输送容量不足时，配套风光可以进行削减。

式中，pw,f,t为外送风光w在时刻t的预测值。

对于送端电网的电力交易，根据交易签订时的约定，可分为电量交易和电力交易。电量交易仅需保证全天电量符合交易值即可。

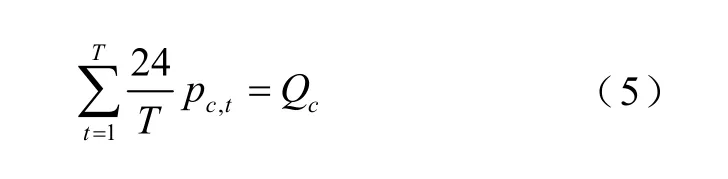
式中，Qc为交易c的交易电量。式（5）给出了以电量为交易目的的外送电量约束。

不可更改的电力交易，则以固定出力进行约束。对于可调整交易，需满足交易调整上、下限约束。

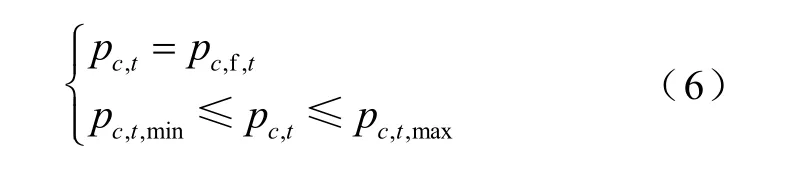
式中，pc,f,t为交易c在时刻t的固定交易值；pc,t,max、pc,t,min分别为交易c调整的上、下限值，该值将作为送端电网计划编制的边界条件。

2.3 直流运行约束

直流运行需要满足一定的运行约束，主要包括直流限额约束、直流爬坡约束及直流出力平滑约束。

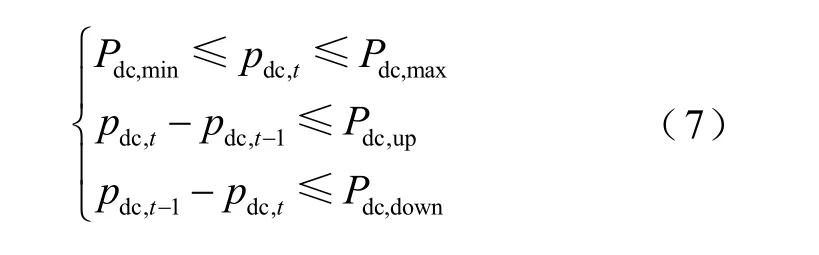
式中，Pdc,max、Pdc,min分别为直流出力上、下限；Pdc,up、Pdc,down分别为直流爬坡速率上、下限。本文中，Pdc,max为决策变量，受限于受端电网运行方式。

直流出力平滑约束，是指为保障直流出力的相对稳定，模型可以根据需要，根据人工设置的出力维持时间段，构建功率平滑约束。

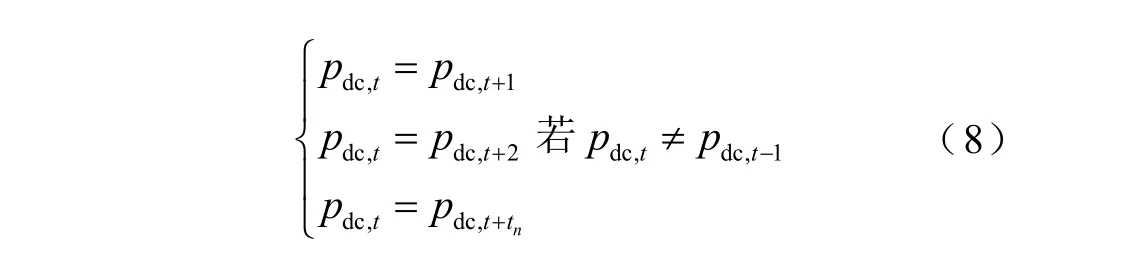
式中，tn为直流需要出力维持的时间段。

2.4 受端电网约束

1）系统平衡约束

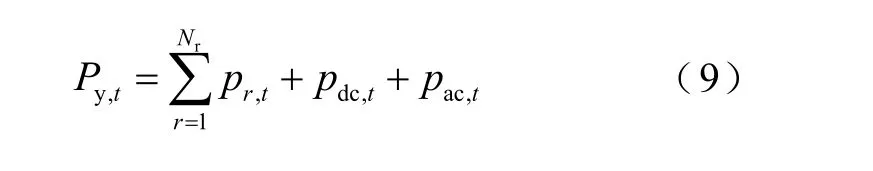
式中，Py,t为时刻t的系统负荷预测值，为已知量；pr,t为时刻t受端电网机组r的出力；Nr为受端电网机组总数；pdc,t为直流在时刻t的受入计划值，它参与受端负荷平衡；pac,t为时刻t受端电网其他外部联络线功率，为已知值。

2）系统备用约束

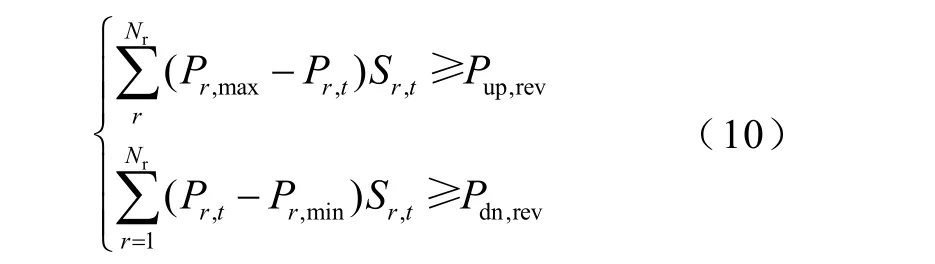
式中，Sr,t为机组r在时段t的开停机状态（1表示开机，0表示停机）；Pr,max、Pr,min分别为机组r的上、下限；Pup,rev为系统的正备用需求；Pdn,rev为系统的负备用需求。

3）机组运行约束

送受端机组均需满足机组运行约束。包括机组出力限值约束、机组爬坡约束、机组最大起停次数约束。

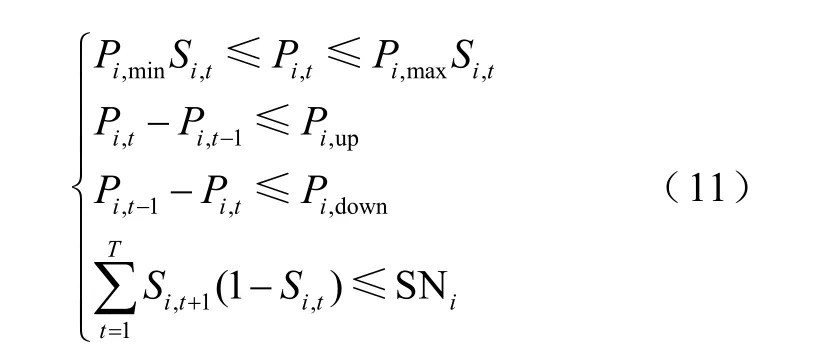
式中，Pi,up、Pi,down为机组i的上爬坡和下爬坡限额。SNi为机组i的最大起停次数。

4）机组开停机时限约束

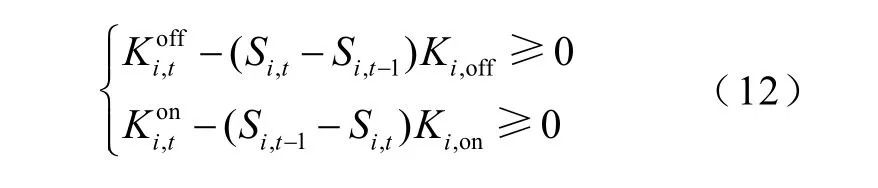
式中，Ki,on为机组i的最小运行时间要求；Ki,off为机组i的最小停运时间要求；分别为机组i已持续或停运时间。

5）支路/断面限额约束

潮流计算模型采用直流潮流法。支路热稳限额约束为

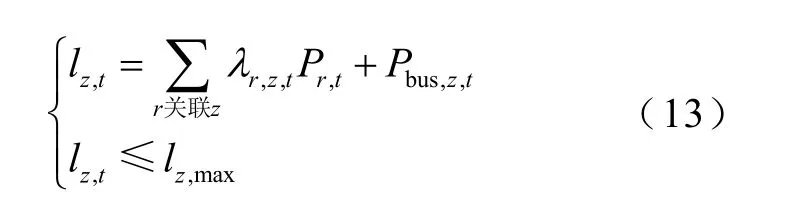
式中，lz,t为支路z在时刻t的潮流；lz,max为支路z的热稳上限；λr,z,t为机组r在时刻t对支路z的有功灵敏度；Pbus,z,t为所有常规母线负荷在时刻t对该支路的潮流贡献，由于母线负荷预测为已知值，可事先通过预测值乘以灵敏度计算获得。

断面限额约束为

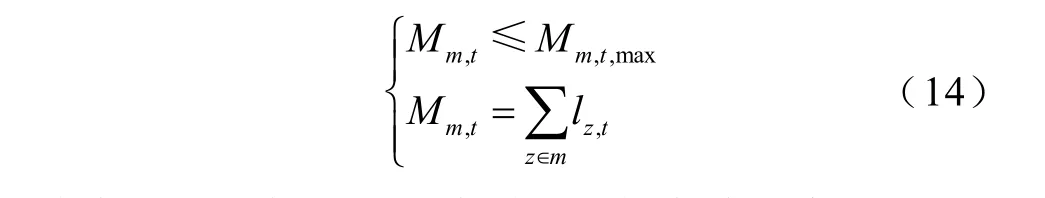
式中，Mm,t为断面m在时刻t的有功潮流；Mm,t,max为断面m在时刻t的方式限额值；z∈m表示断面m的支路构成。

6）直流动态限额约束

在传统的风光火打捆外送或SCUC模型中，直流限额均为已知值，本文提出将Pdc,max定义为“动态”边界，其与受端机组开机、系统备用等因素相关联。

定义直流限额为

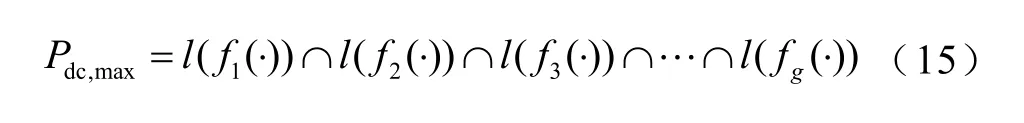
式中，Pdc,max为根据外部因素优化得到的限额值；l(f1(·))、l(f2(·))、l(fg(·))分别为不同因素计算得到的限额结果；∩表示集合交集运算。如果式（15）仅由三个因素决定，f1(·)表示机组开机台数总和，f2(·)表示机组开机容量总和，f3(·)表示系统正备用容量，那么式（15）的物理意义表示根据机组开机台数、开机容量和系统正备用可分别计算得到直流的限额，再对限额求交集即可得到直流的最终限额。

每一个l(f(·))均可表示成决策变量表达式，例如将其表示为开机容量时，首先需要将f(·)写为

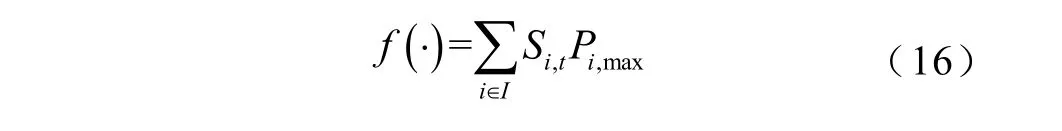
l(fg(·))的取值是通过判断fg(·)的取值范围给定。通常为分段函数，即

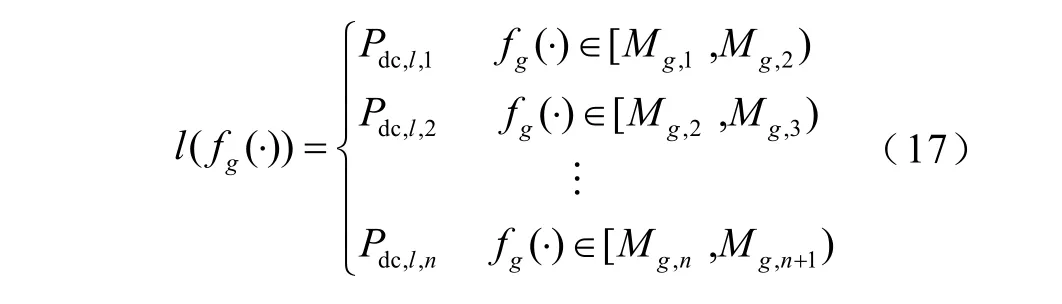
式中，Pdc,l,n为直流受限于因素g在第n段的限额值，为已知量；Mg,n、Mg,n+1分别为决策变量fg(·)表达式的取值区间上、下限值，为已知量。

2.5 决策变量相互耦合的复杂逻辑约束处理策略

传统的风光火打捆外送或机组组合模型，将开机费用、发电费用曲线分段线性化后，将其模型转换为混合整数规划模型，采用成熟商业软件（如CPLEX）可直接求解。本文引入直流限额动态调整后，式（15）～式（17）为决策变量表达式，在决策变量求解前，无法判定的f(·)取值范围，因此式（15）～式（17）虽然能够直观地表示物理意义，但却不能进行直译形成满足混合整数规划特征的模型。在此，本文通过引入0-1“定位”变量进行模型改建。

由于l(f(·))为分段函数，因此需要引入0-1“定位”变量，确定l(f(·))所处分段区间，从而获得限额值。对于每一个l(f(·))定义0-1“定位”向量yl,n，其中n表示第l(f(·))因变量表达式将“动态”限额分成了n段。

此时的对应第g个因素的fg(·)表达式为

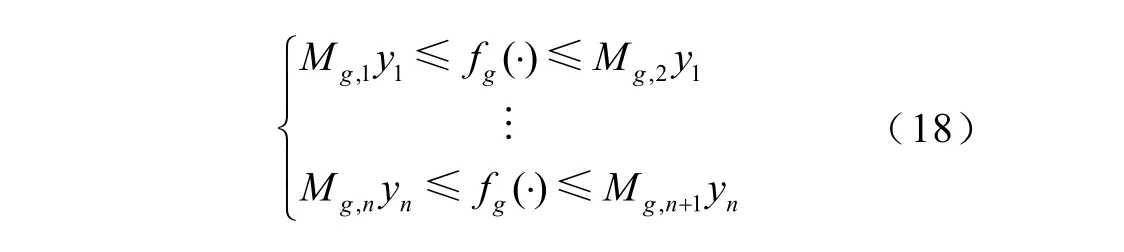
此时l(fg(·))对应的“动态”限额可表示为

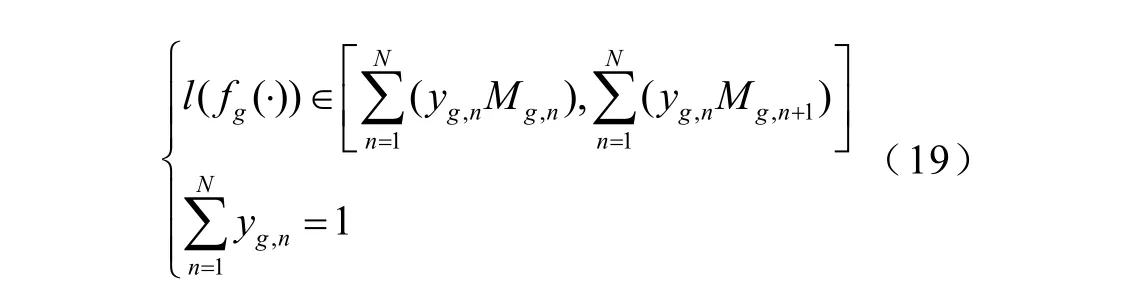
式（19）表示l(f(·))求得的“动态”边界只能处于n个分段中的某一段。

现以表2中开机容量和正备用容量对限额的影响进行举例说明。限额由于两个因素，被分成5段，引入0-1“定位”变量为25× 的Y矩阵。以开机容量为例，不同的开机容量值应满足

限额对应值为

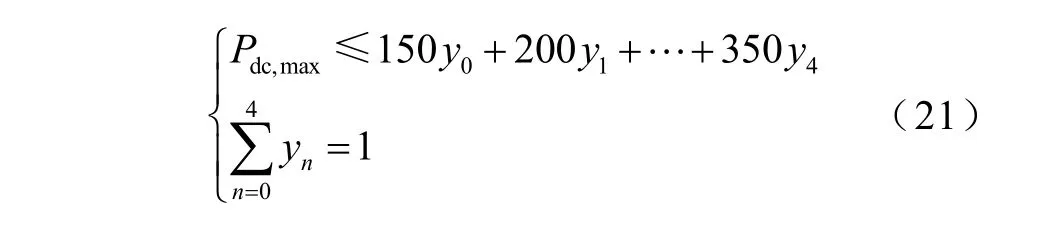
通过式（21）可知，如果Pdc,max取值200MW，则对应y1=1，此时根据式（20），第2段开机容量约束生效，对应为

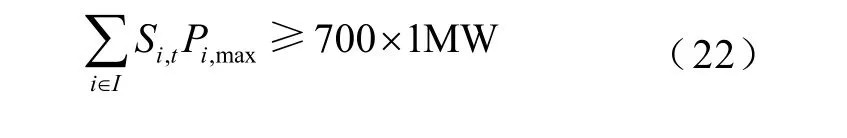
这样就实现了根据开机容量动态确定直流限额的目标。以同样的方式可以列写正备用容量约束，在此不再赘述。

综上所述，将所涉及的l(f(·))表达式均按照式（18）、式（19）进行模型构建，可自动满足式（15）中的交集运算。且转换后的表达式（18）、式（19）满足混合整数规划模型的特征，可采用商业软件进行直接求解。

3 算例及其分析

为验证本文所提模型的有效性，将模型和算法应用于IEEE新英格兰10机39节点标准算例[13]和我国某省实际电网算例。

3.1 新英格兰10机39节点标准算例

为测试本文所提模型的有效性，需对10机39节点算例进行调整。调整方式为：在节点16接入直流线路，连接外部电网。外部电网包括风光等值机组1台，配套火电3台及电力汇总交易1笔。其中风光预测值如图1所示。配套火电的运行和经济参数与原有10机系统中的机组5、机组6、机组7一致，为保证配套火电对风电波动的响应能力，配套火电1处于开机状态。交易为电量交易，全天交易电量为480MW·h。直流线路方式限额见表2。

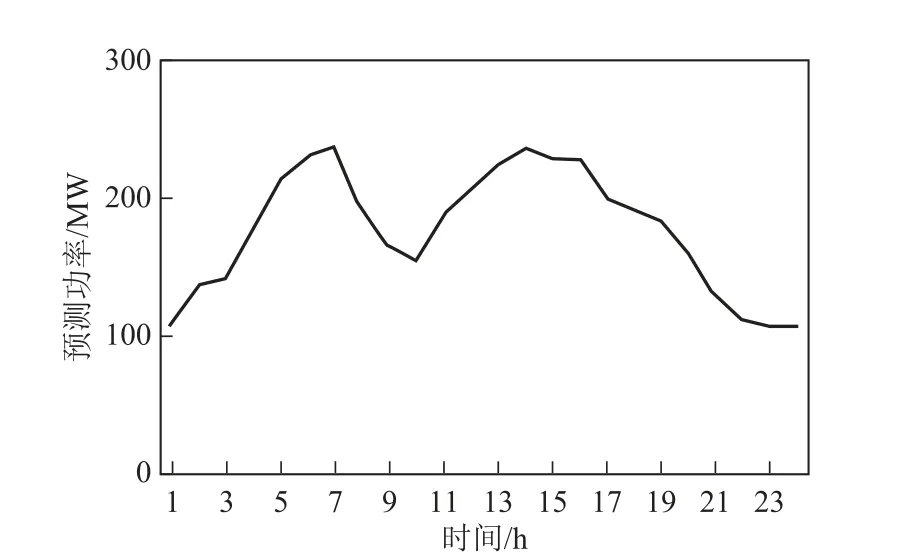
图1 风光预测值Fig.1 Wind and PV forecasts

表2 直流方式限额 Tab.2 DC transmission section limit （单位：MW）

3.1.1 保守限额下送受端一体化计划编制测试

本次测算中，直流线路采用保守的限额250MW，按照本文所提模型，可一次性编制送受端机组及直流计划结果。系统的整体运行费用为496 389$。得 到的直流计划如图2所示，配套风光计划如图3所示，受端电网的出力及备用情况如图4所示。

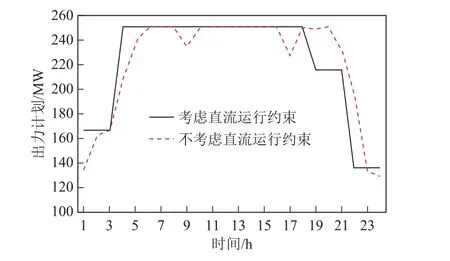
图2 直流计划结果Fig.2 DC schedule results

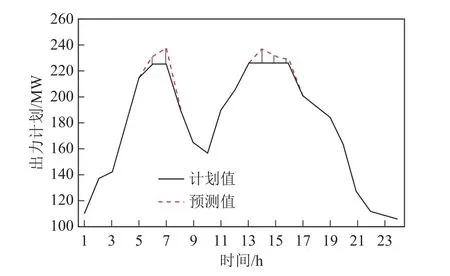
图3 风光电计划结果Fig.3 Wind and PV schedule results

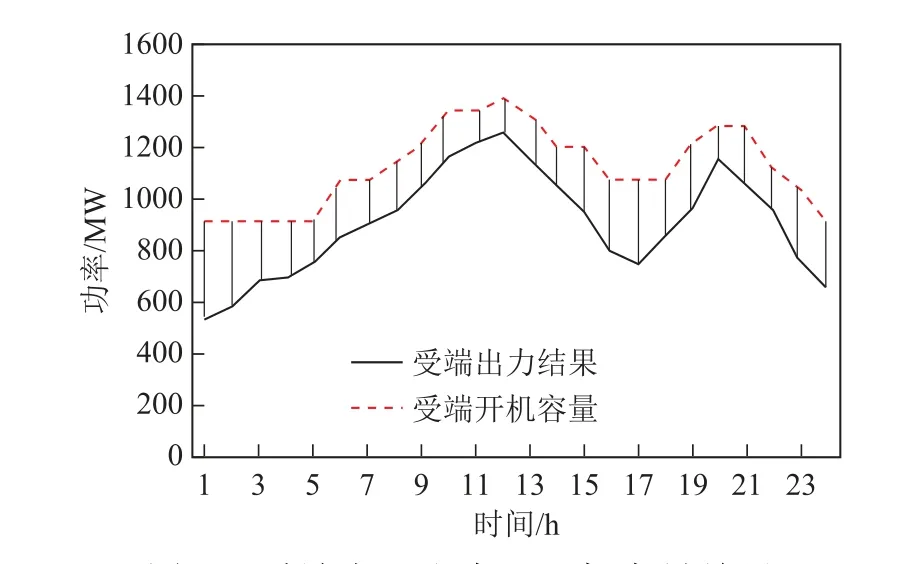
图4 受端电网出力及开机容量结果Fig.4 Results of receiving-end grid output and startup capacity

图2给出了两种条件下的直流计划结果，显然考虑平滑约束后的直流计划具有更好的可执行性。 后续模拟仿真均针对的是考虑直流平滑后的结果。

图3给出了配套风光的预测值和计划值，由于受限于直流输电限额，在风光大发时期存在少量的弃风弃光现象。

3.1.2 动态限额下送受端一体化计划编制测试

本次算例中，直流的限额采用表2所给的动态限额，通过调整受端开机方式可以改变限额值。此时系统的整体运行费用为494 145$，比算例1中的费用降低了763$。算例2中风光全部输送至受端电网。两个算例的直流计划对比、受端系统的正备用对比及受端系统的开机容量对比如图5～图7所示。

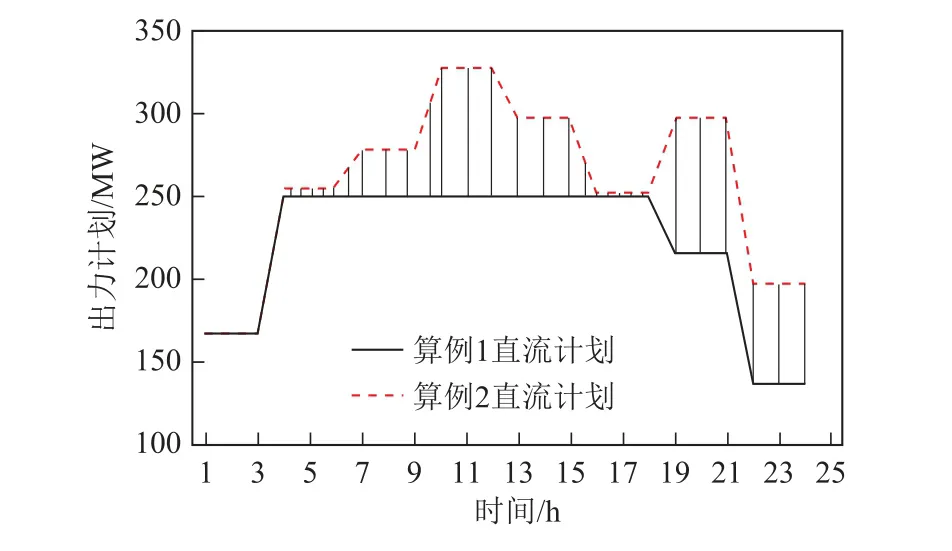
图5 两种方式下的直流计划对比Fig.5 Comparison of DC schedule results in two modes

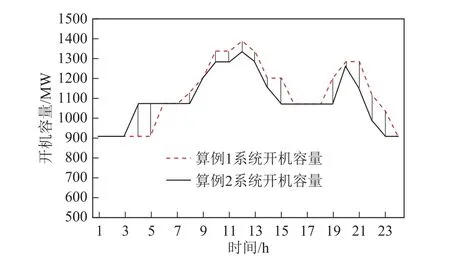
图7 两种方式下的开机容量对比Fig.7 Comparison of startup capacity in two modes

通过图5可知，从第5个弃风的时段开始，直流限额得到了提升。由于配套火电1采用的是原10 机系统中机组5的经济参数，相比于机组7～10具有更佳的经济性。因此提升直流的输电限额，不但可以全额消纳风电，还可以通过增发送端经济机组出力，进一步降低全系统的发电费用。

通过图6和图7可知，为了实现直流限额提升，必须在某些时段增加系统开机容量和正备用。比如在时段4，相对于算例1需要增开1台机组，使得开机容量达到1 072MW。在时段11，算例1中系统正备用为125MW，无法使直流限额达到300MW，因此在算例2中通过调整开机方式，令该时刻的正备用达到160MW，使得正备用满足直流限额300MW的要求。

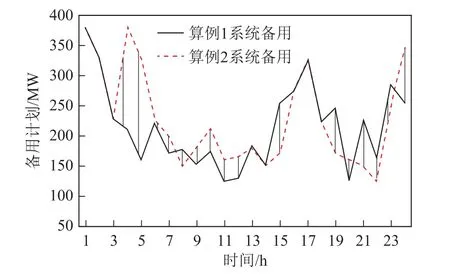
图6 两种方式下的正备用对比Fig.6 Comparison of positive reserve in two modes

3.2 省级电网实际算例

将本文所提的模型应用于我国某实际电网，该电网包含主力火电机组50余台，其中中部火电机组台数总计8台，负荷中心总计20台。该省含有大量水电机组，其通过一条特高压直流承载外部电力输入。本算例将以最大化直流输电利用率为目标进行模型构建。特高压直流输电限额（根据算例仿真计算需求，对真实的直流限额进行了调整，算例中所用数据不代表实际限额）见表1，与中部火电机组和负荷中心火电机组开机台数及系统正备用相关。

按照当天实际确定的开停机结果得到的特高压直流的限额为2 000MW。当28台相关火电机组参与开停状态优化，得到直流限额和直流计划如图8所示。

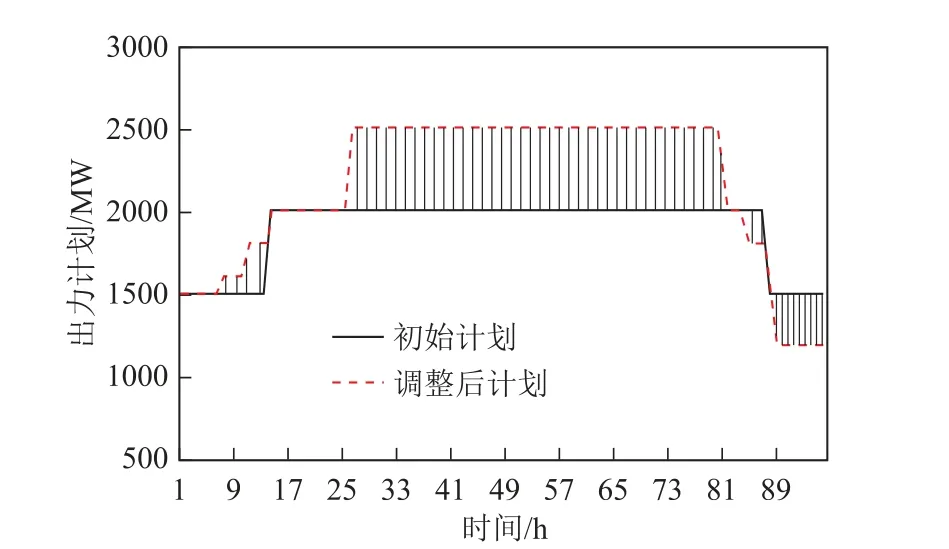
图8 特高压直流出力曲线Fig. 8 Output curves of UHVDC

分析可知，从时段26开始，可以通过中心负荷区增开机组提升直流输电限额和直流利用率。然而由于火电机组的出力下限约束、水电发电需求，使得系统正、负备用约束限制了火电机组开机台数。而从时段89开始，随着负荷需求的降低，相比于原计划，需要进一步降低计划值，使系统满足负备用约束。因此，本算例中直流仅能将限额提升到2 500MW，且不能在全天范围内按限额出力。如果能够发挥库 容水电的调节性能，提升常规火电的深调能力，则可以进一步提高直流利用率，提升系统运行经济性。

4 结论

本文将开机台数、开机容量、备用容量等因素对直流方式限额的影响纳入机组组合模型，构建了计及直流限额动态调整的送受端一体化日前计划模型，并针对模型中约束边界条件随决策变量变化的问题，给出了相关处理策略。将所提模型应用于标准算例和我国实际电网，可得到以下结论：

1）模型可以在机组组合中考虑方式限额的动态变化。通过限额按需自动调整，可有效释放输电能力，提高直流利用率，提升电网运行经济性。

2）模型可以一次性求得满足电网安全及运行需求的送端配套电源、直流及受端电网计划，可提升计划编制效率。