交直流混合激励下取向硅钢片磁滞及损耗特性模拟方法

赵小军 王 瑞 杜振斌 苑东伟 杜海泉

（1. 华北电力大学电力工程系 保定 071003 2．河北省输变电装备电磁与结构性能重点实验室 保定 071056 3．国网聊城供电公司 聊城 252000）

0 引言

软磁材料因具有高磁导率和低损耗等特性，被广泛应用于电力设备和电子器件中[1]。大型电机、变压器、电抗器等设备的铁心，都是由硅钢片叠制而成，工作在工频正弦激励下。然而随着直流输电技术的快速发展与电力电子器件的广泛应用，电力系统中引入了直流偏磁和大量谐波，软磁材料的磁通发生畸变，导致铁心振动加剧、局部过热，同时危害电力系统安全稳定运行。因此较为准确地模拟交直流混合等复杂激励下的软磁材料磁滞与损耗特性对变压器、电机等设备的运行特性和优化设计具有重要意义[2-3]。

国内外学者针对非正弦激励下铁磁材料磁滞及损耗特性开展了大量研究工作。刘任等提出了基于场分离技术与损耗统计理论的新型解析动态Energetic模型，具有较好的拟合精度，但是磁滞模型待提取参数较多[4-5]。李阳等建立动态 Jiles-Atherton（J-A）模型，提出基于粒子群算法与遗传算法的混合算法实现模型的参数辨识，该方法在单纯的直流偏磁激励下拟合效果较好，然而当偏磁与2次或3次谐波均存在时，动态磁滞回线形状拟合误差较大[6-7]。S. Hussain等利用Preisach模型进行高频正弦及谐波激励下的磁滞特性模拟，同时实现与数值计算相结合，模拟精度较高，但参数辨识过程较为复杂，不易掌握和实现[8-11]。赵志刚等结合商用电磁场数值分析软件提出考虑畸变磁通影响的谐波磁损耗工程计算方法[12]，李琳等将主磁滞回环及其内部偏置小回环独立考虑，推导了磁滞损耗和剩余损耗统计参数的半解析表达式，计算出含小回环的3次及5次谐波激励下的损耗[13]。刘刚等对原始损耗分离模型中的损耗分量进行系数校正，使其可以应用于基波叠加单次谐波激励下的损耗计算[14-15]。

综上可知，针对非正弦激励下的磁特性模拟和损耗计算的研究还不够深入，仍然存在一系列问题：

1）磁滞模型大多要基于测定的磁滞曲线，采用优化算法得到拟合参数，当激励形式较为复杂时，很难得到合适的参数，导致模型预测能力较弱。

2）对于谐波下的研究主要针对损耗的拟合，并没有同步实现动态磁滞特性的模拟，限制了应用范围。

3）研究的激励形式大多为直流偏磁或谐波的单一类型，而实际工程变压器常运行在偏磁与多谐波共同激励的条件下，此时铁磁材料的磁滞回线出现非对称性，并同时可能出现局部回环，很难进行有效且准确的动态磁滞和损耗特性模拟。

本文基于BROCKHAUS 磁性能测量系统，获得了取向硅钢叠片在偏磁与谐波叠加激励下的磁滞与损耗特性，并对激励中各变量对损耗特性的影响进行研究。基于Preisach磁滞模型，提出了面向非对称磁滞回线模拟的参数辨识方法，并应用于静态磁滞特性模拟。进一步考虑直流偏磁磁场和谐波次数激励各变量对异常损耗参数V0的影响，构建适用于交直流混合激励下磁性能模拟的动态磁滞模型。分析对比了动态磁滞回线及损耗的仿真结果与实验测量结果，对本文提出的方法进行验证。

1 交直流混合激励下的磁性能测量

1.1 磁性能测量系统

图1所示为多功能磁性能测量平台，包括标准爱波斯坦方圈、电源，以及软件控制系统等。软件控制系统负责将通过PC端输入的控制指令（波形、直流偏磁磁场强度、谐波次数、交流磁通密度幅值等）进行数据处理，施加相应激励。一次绕组的选择性励磁可通过自由曲线或脉冲宽度调制信号实现，经由功率放大器提供。励磁电流i(t)与磁场强度H(t)满足安培定律，即

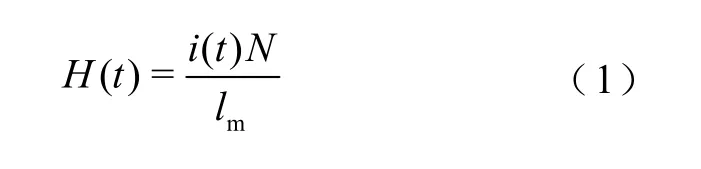
式中，N为爱波斯坦方圈的线圈匝数，实验中一次、二次侧线圈匝数均为128；i(t)为一次绕组励磁电流；lm为等效磁路长度。

在一次绕组中通入直流电流idc，在铁心中建立直流磁场Hdc，二者间仍有式（1）所示线性关系。同时在绕组端口施加谐波电压u(t)，磁通密度B(t)的测定是通过对二次绕组感应电压u2(t)的采样、转换和积分来实现的，u(t)和B(t)的表达式分别为

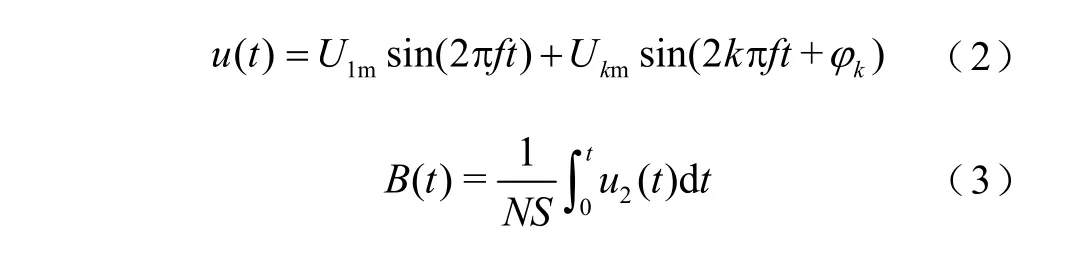
式中，u2(t)为二次侧感应电压；U1m为基波电压幅值，Ukm为第k次谐波激励电压幅值；f为基波频率；kφ为第k次谐波与基波之间的相位差，本文选取kφ=0°；S为样品等效截面积。

使用独立的模拟数字转换器并行记录样品H(t)和B(t)的大小，以避免相位差产生的误差。测试样品参数见表1。

表1 硅钢叠片样品参数Tab.1 Some key parameters of the silicon steel lamination

1.2 偏磁与谐波对磁滞及损耗的影响

直流偏磁存在时，基波叠加高次谐波时测量得到的动态磁滞回线分别如图2a、图2b所示。由图2可知，激励中直流偏磁和谐波的同时存在，会导致磁滞回线不对称并可能出现局部回环，磁化特性更加复杂。因此要基于实验数据预先进行损耗特性分析。

图2 实验测量的动态磁滞回线Fig.2 Dynamic hysteresis loop of experimental measurement

图3给出了不同直流偏磁作用下，基波叠加7次谐波激励时的损耗曲线。当直流磁场强度Hdc不变，损耗会随着交流磁通密度峰值Bacm的增大而明显升高；当Bacm不变，伴随着Hdc每增长25A/m，损耗也会增大，但增长速率越来越缓慢。因此直流偏磁磁场的存在会使损耗增大，同时对于损耗特性的影响具有饱和性。Hdc=75A/m，基波叠加不同高次谐波时的损耗曲线如图4所示。损耗随着所叠加谐波次数的升高而增大，并且次数越高，增长速率越快。因此激励中谐波的存在会促使损耗升高，并且其频率对损耗特性的影响较为显著。当直流偏磁磁场与谐波次数均发生改变时的损耗曲线如图5所示。k=3，Hdc=25A/m的损耗曲线和k=5，Hdc=0A/m的损耗曲线在A点相交，可见当外加激励中直流偏磁作用增强，但基波叠加的谐波次数降低（亦可视为谐波作用减弱）时，损耗的变化将会与交流磁通密度峰值Bacm直接相关，若Bacm较低，直流偏磁磁场 作用更明显，损耗升高；反之，则谐波作用更明显，损耗降低。究其原因，当铁磁材料交流磁通密度较低，对应的磁场强度随之降低，此时施加Hdc对损耗的升高作用显著，k减小对损耗的降低效果则相对而言较弱；反之材料在交流磁通密度比较高时已经趋于饱和，而实验中所施加的直流偏磁磁场强度Hdc最大仅为100A/m,远小于饱和磁场强度，偏磁影响不明显，谐波则成为影响损耗变化的主要因素。

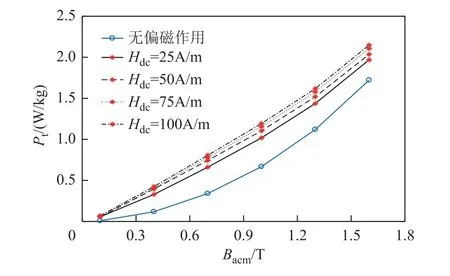
图3 基波叠加7次谐波在施加不同直流偏磁时的 损耗曲线Fig.3 Loss curves under different DC bias when the seventh harmonic is superposed on the fundamental component in the hybrid excitation

图4 Hdc=75A/m，基波叠加不同的高次谐波时的 损耗曲线Fig.4 Loss curves when different frequency of harmonic is superposed on the fundamental component in the hybrid excitation with Hdc=75A/m

图5 无偏磁作用和Hdc=25A/m时，基波叠加3次或5次谐波的损耗曲线Fig.5 Losses curves when third or fifth harmonic is superposed on the fundamental component in the hybrid excitation with Hdc=0A/m or Hdc=75A/m

由以上结果及分析可知，在交直流复合激励条件下，硅钢片的磁滞及损耗特性较为复杂，需要结合激励特征建立有效且准确的磁滞模型。

2 交直流混合激励下的动态磁滞模型

根据G. Bertotti提出的损耗统计理论[16]，直流偏磁与谐波相叠加的混合激励下单位时间内每单位体积硅钢片的总损耗由磁滞损耗Ps,hy、涡流损耗Ps,cl和异常损耗Ps,ex三部分组成，即

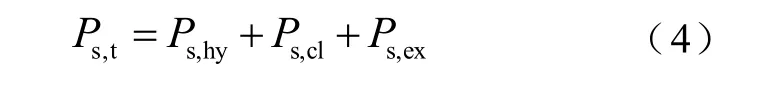
式（4）中Ps,cl为直流偏磁与谐波叠加激励下的涡流损耗，假设磁场沿磁性材料内部均匀分布，基于麦克斯韦方程得到其表达式为

式中，σ为材料电导率；d为叠片厚度；Ws,cl为时间周期T范围内的涡流损耗。需要注意的是，本文激励所叠加的谐波频率较低（小于500Hz），故趋肤效应可以忽略不计[17]。

式（4）中Ps,ex为直流偏磁与谐波叠加激励下的异常损耗。异常损耗是由于磁畴壁的移动在其附近感应出的微观局部涡流而产生，与动态磁化过程紧密相关，目前难以利用实验手段对其物理机理进行准确测量。因此基于磁畴理论推导得到异常损耗的数学模型为[18]

式中，S为叠片的横截面积；G为无量纲系数，G=0.135 6；V0为表征局部磁场分布的统计参数，用来描述材料的微观结构特征；Ws,ex为时间周期T范围内的异常损耗。

式（4）中Ps,hy为直流偏磁与谐波叠加激励下的磁滞损耗。传统损耗模型并未对其给出解析表达式或有效求解方法，因此复杂激励形式下磁滞损耗的计算是损耗分离模型存在的重点问题。一般正弦激励下磁滞损耗计算表达式为

式中，Psin,hy为正弦激励下的磁滞损耗；kh和α为磁滞损耗系数；fm为激励频率；Bm为磁感应强度峰值。为了拓宽该式的适用范围，M. Popescu等提出将磁滞损耗系数用Bm的多项式进行拟合，有效地改善了精度[19]。然而单纯的损耗拟合无法考虑磁滞效应，不能与有限元方法相结合，应用在铁磁材料的局部磁特性研究时具有明显局限性。综上可知，应利用有效准确的磁滞模型对交直流混合激励下的磁滞特性进行模拟。

基于场分离技术，可将直流偏磁与谐波相叠加激励下的动态磁场强度Hs,t分为三个部分[20-21]，即

式中，B为直流偏磁与谐波叠加激励的磁感应强度；Hs,hy、Hs,cl和Hs,ex分别为磁滞损耗、涡流损耗和异常损耗对应的磁场强度。Hs,cl、Hs,ex与损耗的关系为

根据场量和能量之间的关系，涡流损耗Ws,cl和异常损耗Ws,ex在极小时间段dt内的微小增量dWs,cl和dWs,ex分别为

将式（11）与式（13）、式（12）与式（14）结合，可推导得到

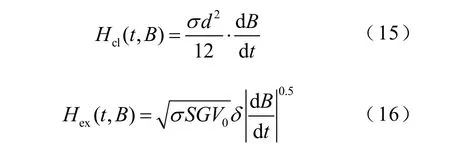
式中，δ= sign(dB/dt) = ±1，取决于磁感应强度B随时间变化的曲线是上升还是下降。

3 静态磁滞模型及其参数辨识

用于软磁材料磁滞特性模拟的磁滞模型有Jiles-Atherton（J-A）模型、Preisach模型、Energetic模型及E&S模型等[4-11,22-25]。本文选择具有较高求解精度的Preisach模型，建立模型的基本步骤为：①生成一阶回转曲线；②利用一阶回转曲线辨识如式（17）所示的Everett函数；③由式（18）计算得到磁场强度H的输出值[10]。

式中，B和b分别为上升和下降的磁感应强度局部极值；以起始于上升支的一阶回转曲线为例，Hforc(B)为位于上升支输入值为B的点所对应的输出值，Hforc(B,b)为起始于上升支为B的点的一阶回转曲线，输入减小到b点时对应的输出值。

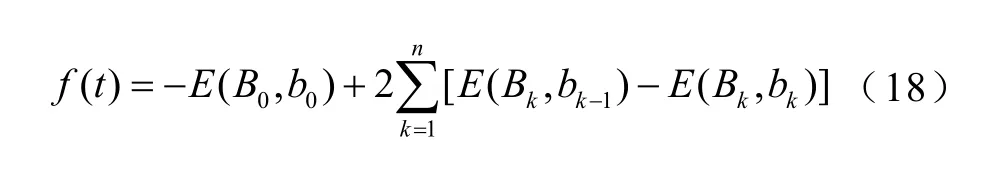
式中，E(Bk,bk-1)为对应于上升的局部极值k=1,2,…,n处的逆Everett函数值；E(Bk,bk)为对应于下降的局部极值k=1, 2, …,n处的逆Everett函数值；E(B0,b0)为正向饱和状态时对应的逆Everett函数值。

铁磁材料的一阶回转曲线（FORCs）是利用Preisach模型解决静态磁滞特性模拟问题的关键。E. Dlala提出了基于对称的极限磁滞回线生成一阶回转曲线的数值方法[8]，但该方法具有局限性，即要求用于生成一阶回转曲线的极限磁滞回线必须具有对称性。而在交直流混合激励下，由于偏磁的影响，通过实验测量得到的是非对称极限磁滞回线。S. E. Zirka等提出了另一种数值方法，并将其应用于无偏磁作用下软磁材料的磁滞与损耗特性模拟[26]。事实上，这种新的一阶回转曲线的数值生成方法具有更佳的泛化能力和更广的适用范围，能够用于非对称一阶回转曲线的生成。本文将采用该方法构造交直流混合激励下非对称极限磁滞回线的一阶回转曲线。

通过实验可测量得到Bacm=1.88T，不同直流磁场强度Hdc时的静态极限磁滞回线。由于测量系统不能直接获取硅钢片中磁通密度的直流分量，本文采用迭代法[27]计算得到不同偏磁情况下磁通密度直流分量。利用上文提到的数值方法分别生成起始点位于上升支的下降的一阶回转曲线和起始点位于下降支的上升的一阶回转曲线，如图6所示。进而可以得到考虑了磁滞特性非对称特征的逆Everett函数E(bu,bv)，如图7所示。

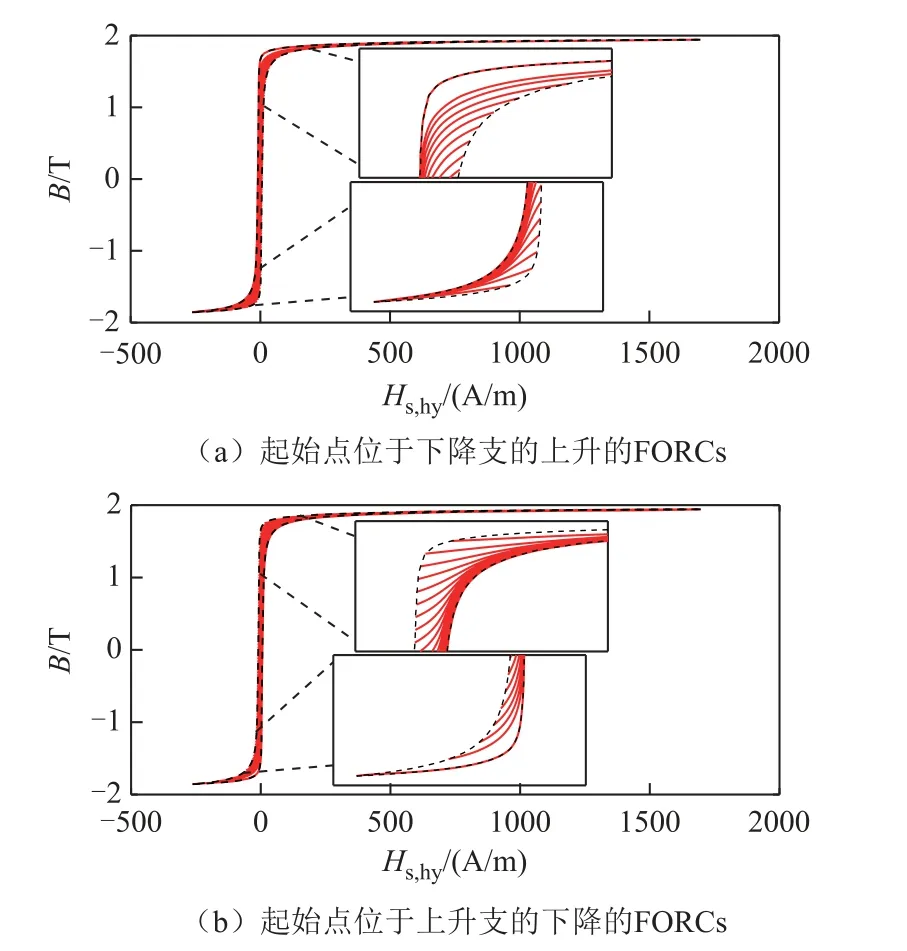
图6 一阶回转曲线Fig.6 The FORCs

图7 逆Everett函数Fig.7 Inverted Everett function composed from FORCs

基于非对称的逆Everett函数建立Preisach磁滞模型，对不同交直流混合激励情况下的静态磁滞回线进行拟合，图8给出了工况a（k=5，Bacm=1.0T，Hdc=50A/m）及工况b（k=5，Bacm=1.3T，Hdc=100A/m）仿真结果与实验结果对比。可以看出磁滞回线主回环拟合效果良好，但部分局部回环拟合效果欠佳。究其原因，受到实验条件的制约，无法通过测量得到真正的静态磁滞回线，实验中只能用较低频率下（基频3Hz）的交直流混合激励来近似获得静态磁滞回线。通过式（2）和式（3）可知，交流磁通密度基波部分的实验激励频率为3Hz，满足近似条件；而谐波部分的实验频率会随着谐波次数k的升高而增大，在7次谐波时达到了21Hz。虽然和动态实验的基频50Hz相比并不高，且当谐波含量较低时，谐波在磁滞回线生成过程中的作用明显小于基波作用，不会对主回环产生很大影响，但是却会直接影响局部回环的测量结果，导致局部回环的测量值与其实际值存在一定偏差。

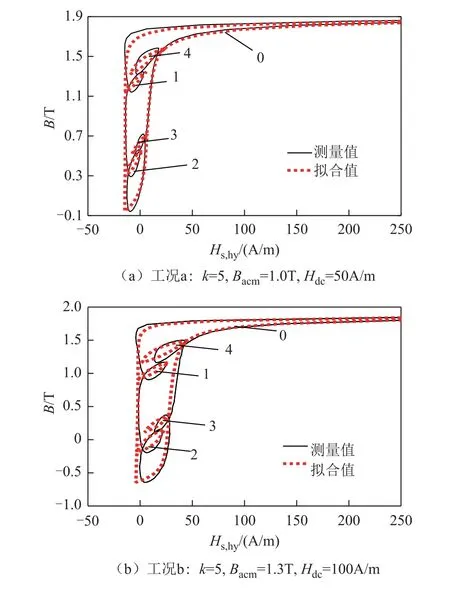
图8 静态磁滞回线测量与拟合对比Fig. 8 Comparison between measured static hysteresis loops with simulated ones

为了更好地评价拟合效果，应从损耗的角度对图8两组工况的静态磁滞模拟进行误差分析，结果见表2，P0、P1～P4分别表示主回环和局部回环1～4的磁滞损耗；Ps,hy表示静态磁滞损耗；Δr代表拟合值的相对误差。可以看出，主回环的损耗相对误差控制在10%以内，拟合效果很好；局部回环的拟合效果欠佳，相对误差在20%以内。由于局部回环损耗远小于主回环损耗，前者误差对静态磁滞损耗的计算影响较小，总的磁滞回线对应的损耗误差依旧小于10%，说明本文提出的基于非对称极限磁滞回线生成FORCs，进而构建Everett函数的方法可以用于硅钢叠片在交直流混合激励下的静态磁滞特性的准确模拟。

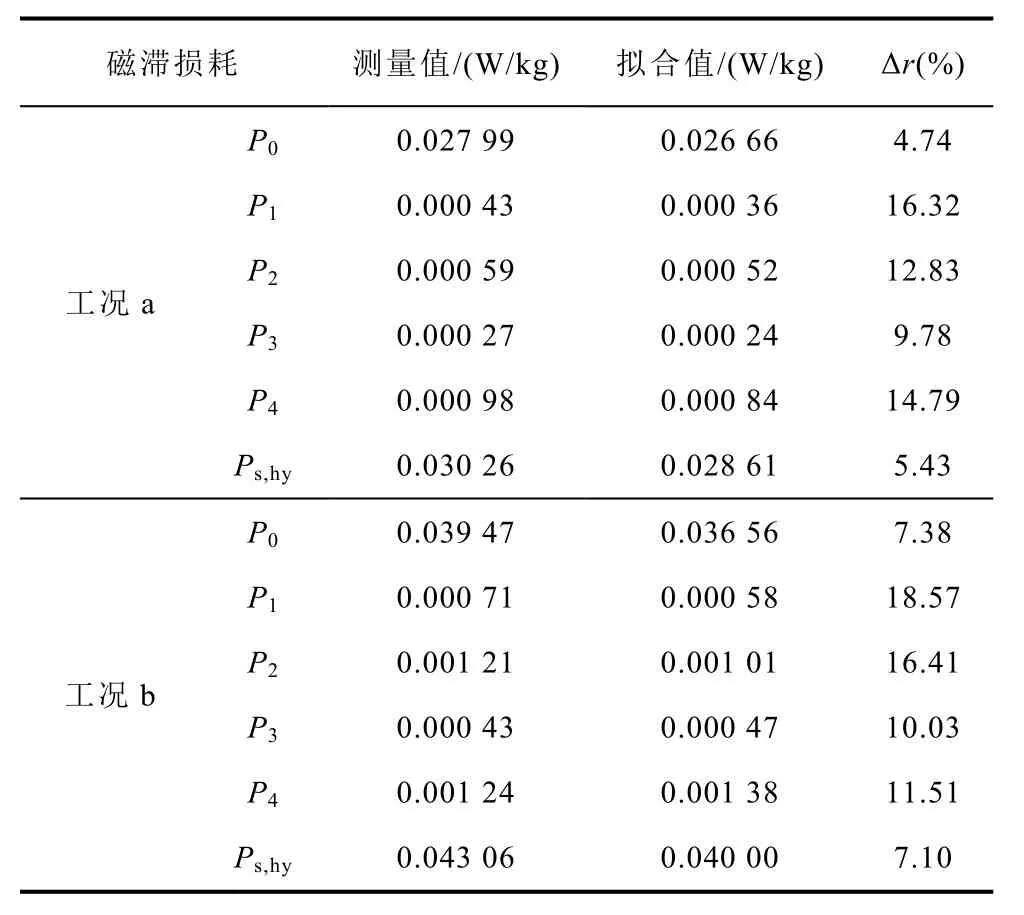
表2 静态磁滞损耗误差分析Tab.2 Error analysis of static hysteresis loss

总体来说，可以通过提升实验条件，降低激励的基频，同时优化Preisach模型，改进Everett函数的生成方法等举措进一步提高静态磁滞特性的模拟精度。

4 动态模型参数提取与磁滞模拟

针对本文施加的交直流混合激励，涡流损耗对应的磁场强度Hs,cl与直流偏磁磁场Hdc无关，只与瞬时磁通密度B(t)随时间的变化率有关，可以直接由式（15）计算。通过式（16）可知，计算异常损耗对应的磁场强度Hex的关键在于准确拟合异常损耗统计参数V0。在直流偏磁激励情况下，V0不仅与交流磁通密度峰值Bacm有关，还与直流偏磁磁场强度Hdc相关[21]。由于本文激励中含有谐波成分，需要考虑谐波次数k可能对V0产生的影响。

4.1 异常损耗的模拟与参数提取

借助动态磁滞实验及静态磁滞模型，得到异常损耗Ps,ex的实验值并提取一系列的V0值，在分析V0随Bacm、Hdc及k变化规律的基础上，通过数值拟合的方法确定函数V0（Bacm,Hdc,k），从而为软磁材料在不同交直流混合激励下的异常损耗预测奠定基础。

在不同交流磁通密度峰值Bacm及谐波次数k下参数V0的变化曲线如图9所示。

图9 Hdc=50A/m，基波叠加高次谐波的V0提取值 变化曲线Fig.9 Extracted value of V0 when higher order harmonic is superposed on the fundamental component in the hybrid excitation with Hdc=50A/m

由图9中V0提取值的变化趋势可以看出，当磁感应强度交流分量峰值Bacm不变时，参数V0值会随基波所叠加谐波的次数k升高而增大；而当谐波次数k一定时，V0会随着磁感应强度交流分量峰值Bacm增大而降低，并呈现出类似幂指数的变化规律。当直流偏磁磁场强度Hdc变化时，仍存在相似的规律，故不再赘述。根据以上特点，本文选用高斯函数作为V0的函数拟合公式，V0的函数表达式为

式中，ip为关于Hdc的函数，可基于实验数据拟合得到，i=1, 2, …, 8。

在两种直流偏磁磁场下，基波叠加不同谐波激励时，Ps,ex的拟合值与实验值的对比如图10所示。可以看出，异常损耗的拟合效果良好，具有较高的 计算精度。由此说明V0的函数表达式可以满足要求。此外，异常损耗Ps,ex随交流磁通密度峰值Bacm和谐波次数k的增大而明显增大，但受直流偏磁磁场强度Hdc的影响很小：在相同的Bacm和k下，随着Hdc从最小值25A/m增长到最大值100A/m，Ps,ex增长非常缓慢，甚至在个别工况时略有下降。

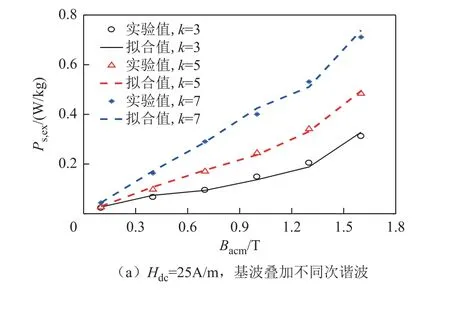
图10 异常损耗实验值与拟合值对比Fig.10 Comparison between measured and fitted excess loss

4.2 动态磁滞特性与损耗特性的模拟及分析

利用前述得到的动态磁滞模型，对型号为B27ZH95的硅钢片在交直流混合激励情况下的动态磁滞回线进行模拟。图11给出三种工况下的动态磁滞回线拟合结果与实验结果对比。

图11 动态磁滞回线测量与拟合对比Fig.11 Comparison between measured dynamic hysteresis curves with simulated ones

可以看出，基于损耗分离辨识动态磁滞模型参数，进而得到的动态磁滞回线与测量结果较为一致，说明本文算法可以对硅钢叠片在交直流混合激励情 况下的动态磁滞特性进行较为准确的模拟。表3和表4分别给出了硅钢叠片在Hdc=25A/m,k=5与Hdc=50A/m,k=7两种不同激励下的铁损计算值Ps,t-cal，并将其与实验测量结果Ps,t-mea对比，发现相对误差Δr在10%以内，损耗计算较为准确，进一步验证了本文模型的准确性和有效性。

表3 Hdc=25A/m, 基波叠加5次谐波激励下铁损测量值与计算值对比Tab.3 Comparison between calculated iron losses Ps,t-mea and measured ones Ps,t-calwhen fifth harmonic is superposed on the fundamental component in the hybrid excitation with Hdc=25A/m

表4 Hdc=50A/m, 基波叠加7次谐波激励下铁损测量值与计算值对比Tab.4 Comparison between calculated iron losses Ps,t-mea and measured ones Ps,t-calwhen seventh harmonic is superposed on the fundamental component in the hybrid excitation with Hdc=50A/m

5 结论

1）交直流混合激励下，直流磁场增大或谐波次数升高均会使损耗增加。不同之处在于，激励中谐波阶数升高对损耗的影响更为显著，而直流磁场增大导致的损耗增大，会受到铁心中磁通密度饱和特征的影响。

2）基于实验测量得到直流偏磁极限磁滞回线，基于两组非对称的一阶回转曲线得到Everett函数，实现了Preisach磁滞模型参数辨识，该模型能够准确地计算静态磁场强度和磁滞损耗。

3）依据直流磁场、交流磁通密度和谐波次数对异常损耗统计参数的影响规律，构造相关函数并进行参数提取，以此得到的动态磁滞模型能够实现交直流混合激励条件下动态磁滞特性及总损耗的准确模拟。

4）本文提出的方法适用于含多个高次谐波的交直流叠加情况，但由于目前实验室仪器等条件的限制尚无法对其模拟精度进行验证，有待于进一步开展深入研究。