A型地铁转向架动力学仿真及滚振试验性能研究

樊庆宇，池茂儒，梁树林，宋宇，于明洋，王欢声

A型地铁转向架动力学仿真及滚振试验性能研究

樊庆宇1，池茂儒1，梁树林1，宋宇2，于明洋2，王欢声1

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 2.北京地铁车辆装备有限公司，北京 100079）

针对北京地铁车辆装备有限公司和西南交通大学牵引动力国家重点实验室设计的120 km/h A型地铁转向架，建立其动力学模型并计算了相关动力学性能指标，分析该转向架设计合理性；基于动力学仿真结果，进一步对该转向架在机车车辆整车滚动振动试验台上进行了滚振动力学试验，并给出车辆在空簧失气故障工况条件下运行时的合理建议。仿真计算与试验结果表明，该A型地铁车辆具有良好的蛇行运动稳定性，在美国V级直线线路上以40～120 km/h速度运行时的平稳性达到优级标准，其临界速度及运行平稳性均能够满足线路上最高运行速度120 km/h的要求，为该转向架上线提供了理论依据及试验参考。空簧失气后，车辆非线性临界速度大幅度降低，安全性指标（轮轴横向力、轮轨垂向力、脱轨系数、轮重减载率）有所增加，而其垂向平稳性指标较原车正常工况明显增大，并且运行速度越高差距越大，若车辆在运行过程中出现空簧失气故障现象，应立即降低车辆运行速度，为保证运行品质，建议限速80 km/h。

A型地铁；蛇行运动；动力学性能；滚振试验

随着科技的快速发展和城市化进程的加快，我国越来越重视交通方面的建设，而安全与便捷是重点考虑方向。在各个城市都存在着交通问题，在人流量和客运量大的城市里尤为突出，因此要寻求最好的交通出行方案，其中地铁的建设能够有效解决此类交通问题，地铁的出现大大缓解了交通压力。地铁列车根据宽度可分为A、B、C三个型号，其中4动2拖6辆编组的A型地铁列车深受大客运量城市的青睐，它采用了高强度、轻量化、大断面的鼓型铝合金车体，3 m的车体宽度，140 m的车体长度以及2520人的客运量让A型地铁列车享有地铁家族“巨无霸”的特殊称号，目前许多有着优秀地铁开发环境的城市都在大力推广A型地铁的建设与开发[1]。

北京地铁车辆装备有限公司和西南交通大学牵引动力国家重点实验室设计的120 km/h A型地铁转向架是一种新型转向架，这类新型转向架一般要经历计算机动力学仿真分析－实验室滚动振动试验－环形线路试验这三个过程，并且试验结果达标才能正式上线并投入运营。故本文在充分了解其结构特征参数以及悬挂特性参数的基础上，建立其动力学模型并计算相关动力学性能是否满足该车辆运行要求；同时将试验转向架运送至机车车辆整车滚动振动试验台，进行滚振动力学试验。结合动力学仿真结果与滚振动力学试验结果，评估该转向架的设计合理性，同时初步分析空簧失气故障工况下的动力学性能指标并提出合理运营建议，给出限速范围，为后续更深入的空簧性能优化分析打下基础。

1 转向架结构分析

该A型地铁转向架的构架为整体H型焊接结构，主要包括两根侧梁和两根横梁。构架侧梁是封闭的箱体，其下侧设置有一系橡胶簧圆筒、转臂定位座，上部设置有空气弹簧座、一系垂向减振器座。中间的两根横梁为钢管结构，电机、齿轮箱吊座、牵引座以及二系横向减振器座斜对称布置在两根横梁的外侧，同时，横向止档座布置在横梁之间，整体的构架结构图如图1所示。

图1 构架结构图

转向架的悬挂方式采用两系悬挂，即一系螺旋钢弹簧组与二系空气弹簧的组合，由空气弹簧直接支撑车体，构架上设置有抗侧滚扭杆和二系横向减振器；轮对轴箱定位装置采用转臂定位结构；牵引装置采用Z字型布置的牵引拉杆结构；采用具有非线性特性的二系横向缓冲橡胶止挡，可设置适当的自由间隙。

2 动力学仿真分析

2.1 车辆动力学模型

车辆系统是一个大型且复杂的多体系统，轮轨之间存在着复杂的作用关系、车辆内部的各部件之间存在着相互作用力和相对运动、车辆与外部载荷之间也有着不可忽视的作用关系。因此，理论计算分析模型必须适情况对一些次要因素进行符合条件的假定或简化，对主要因素尽可能作出符合实际运营情况的模拟和仿真，以此来达到研究的主要目的和要求[2-3]。

图2 车辆动力学模型

基于该A型地铁转向架的结构特征以及整车悬挂系统的悬挂特性，建立了其整车动力学模型（包括空气弹簧的力学模型[4]），如图2所示。该A型地铁由1个车体、2个构架、4个轮对、4个电机、4个齿轮箱和8个转臂组成。车体取6个自由度，即纵向、横向、垂向、侧滚、点头、摇头；构架取6个自由度，即纵向、横向、垂向、侧滚、点头、摇头；轮对取6个自由度，即纵向、横向、垂向、侧滚、点头、摇头（其中轮对垂向和侧滚运动是非独立运动）；电机取3个自由度，即纵向、横向、垂向；齿轮箱取1个自由度，即点头；转臂取1个自由度，即点头。综上，该车辆动力学模型共有66个自由度，如表1所示。

2.2 运行稳定性

车辆系统的蛇行稳定性是系统本身的固有属性，它用来评估车辆能否在高速运营状态下保持优秀的稳定性，其在直线轨道上的稳定性特性通常具有图3所示的两种主要形式（亚临界分岔、超临界分岔），图中实线表示稳定平衡位置（稳定极限环），虚线则表示不稳定平衡位置（不稳定极限环）[5-6]。

表1 京车A型地铁每节车的自由度

图3 蛇行运动极限环

图中点的车速值V定义为线性临界速度，可通过建立车辆系统线性化数学模型来求得，线性临界速度只有在具有极微小激扰的理想轨道上才会出现，因此，是系统的理想临界速度。拐点是车辆系统等幅蛇行运动出现和消失的分界点，其车速值V定义为非线性临界速度，一般来说，非线性临界速度只会发生在线路条件十分恶劣的环境下，它是整个车辆系统的最低临界速度。由于车辆系统首先在某个速度下出现蛇行失稳的现象与轨道激扰大小有关，通常情况下，线路条件越差临界速度越低，条件越好临界速度越高，这时的速度代表了实际运营线路条件下的实际临界速度。为了保证车辆在所有速度下都能保证不发生蛇行失稳现象，本小节以非线性临界速度作为车辆稳定性的评判标准，分别计算了原车正常工况（悬挂元件无故障）和全车空簧失气工况下的非线性临界速度。

该A型地铁在正常工况以及全车空簧失气工况下的一、四位轮对横移量的仿真计算结果如图4、图5所示。

图4 原车工况轮对横移量（仿真）

图5 全车空簧失气轮对横移量（仿真）

线路条件均为直线轨道（线路激励设置为美国五级谱），并设置40～160 km/h范围内以10 km/h为步长的速度级，首先让车辆在每个恒定速度级下运行且施加400 m的线路激励，然后撤掉线路激励在平直光滑线路上运行一段路程后观察一、四位轮对横移量收敛情况，若不收敛则该速度级即为车辆的非线性临界速度。

正常工况下，车辆在速度为160 km/h时轮对横移量均未出现发散现象（即非线性临界速度高于160 km/h），满足该地铁设计速度要求并具有足够的安全裕量；而当全车空气弹簧出现漏气现象时，车辆在运行速度为150 km/h时撤掉线路激励，一、四位轮对均发散即非线性临界速度为150 km/h，尽管低于原车正常工况下的非线性临界速度，但也远高于该地铁车辆的实际运营速度，符合要求。

2.3 垂向平稳性

空气弹簧作为铁道车辆悬挂系统中非常重要的一个元件，能够改善车辆乘坐舒适度并且提高运行平稳性，特别是垂直振动性能方面有了很大的提高，而当空气弹簧发生失气现象时，其对车辆垂向平稳性指标影响显著，对车辆的横向平稳性指标影响不大。原车正常工况以及全车空簧失气工况下的垂向平稳性的仿真计算结果如图6所示，当全车空簧发生漏气时，车辆的垂向平稳性指标明显变差，且在运行速度高于100 km/h时超过了2.5（优级）的限值；随着运行速度的增加，其垂向平稳性指标整体也呈现增大的趋势，但正常工况下车辆在40～120 km/h速度范围内的垂向平稳性指标均为优级[7-11]。

注：红线2.5的限值代表CB/T5599-2019标准中，客车与动车组的平稳性指标小于2.5时，评定为优级。

2.4 运行安全性

新轮状态和磨耗轮状态下的原车工况、空簧失效一半和全车空簧失效工况下的R500曲线通过安全性计算结果如图7和图8所示，原车工况下车辆曲线通过安全性能优秀，能够满足设计要求；空气弹簧半数失气后安全性略有影响，而空气弹簧全数失气对安全性会有一定程度的恶化[12-13]。

3 滚振试验结果分析

机车车辆整车滚动振动试验台是牵引动力国家重点实验室自行研制的大型试验台，承担着许多重大项目，可进行四轴和六轴机车车辆运行过程的动态模拟，包括在直线和曲线上的运行工况。它采用了先进的滚动、振动试验台相结合的设计方案，可以充分实现高难度高水平的垂向、横向和滚动三维运动于一体的精确耦合。只有将滚动、振动两者充分结合起来，该试验台才能够动态地模拟机车车辆在真实运行线路上的实际情况，既可模拟车辆沿轨道向前的运动，又可模拟轨道的各种不平顺输入。

通过将试验转向架运送至机车车辆整车滚动振动试验台，进行了滚振动力学台架试验，本节对车辆正常工况以及全车空簧失气工况下的运行稳定性和垂向平稳性进行了数据结果的分析，验证动力学仿真结果的规律性。

3.1 运行稳定性

车辆稳定性的试验方式是通过滚振试验台纯滚动试验进行增速（速度级为40～160 km/h，以10 km/h为步长，共13个速度段），当轮对圆周线速度达到某个速度段后施加一分钟激振，激励类型与动力学仿真所用线路轨道谱一致，当轮对出现蛇行运动则找到如图3（b）所示的线性临界速度，然后降速，当速度达到点时，蛇形运动的现象消失，此时点对应的速度为非线性临界速度。

对于最高运行速度为120 km/h的车辆，通常最高线路试验速度为最高运行速度的1.1倍即132 km/h，滚振试验纯滚动时稳定性试验速度应大于最高线路试验速度的1.2倍即158.4 km/h，取整为160 km/h，故稳定性最高试验速度设定为160 km/h。正常工况下，车辆在滚振速度为160 km/h时轮对横移量均未出现发散现象（即非线性临界速度高于160 km/h），满足该地铁设计速度要求并具有足够的安全裕量，正常工况下的一、四位轮对横移量的试验计算结果如图9所示；而将全车空气弹簧放气，当车轮圆周线速度到达110 km/h并施加激励时，轮对出现了大幅蛇行运动，然后撤掉滚轮激振激励并降速，车辆纯滚动时轮对横移量于101 km/h收敛即非线性临界速度为101 km/h，远低于原车正常工况，全车空簧失气工况下的一、四位轮对横移量的试验计算结果如图10所示。试验结果表明，全车空气弹簧失气时，会大幅降低车辆的稳定性，影响车辆运行的安全性，故当车辆在线路上运行时发生空簧失气现象，应立即降低车速以防轮对蛇行运动失稳而引起的安全隐患。

图9 原车工况轮对横移量（试验）

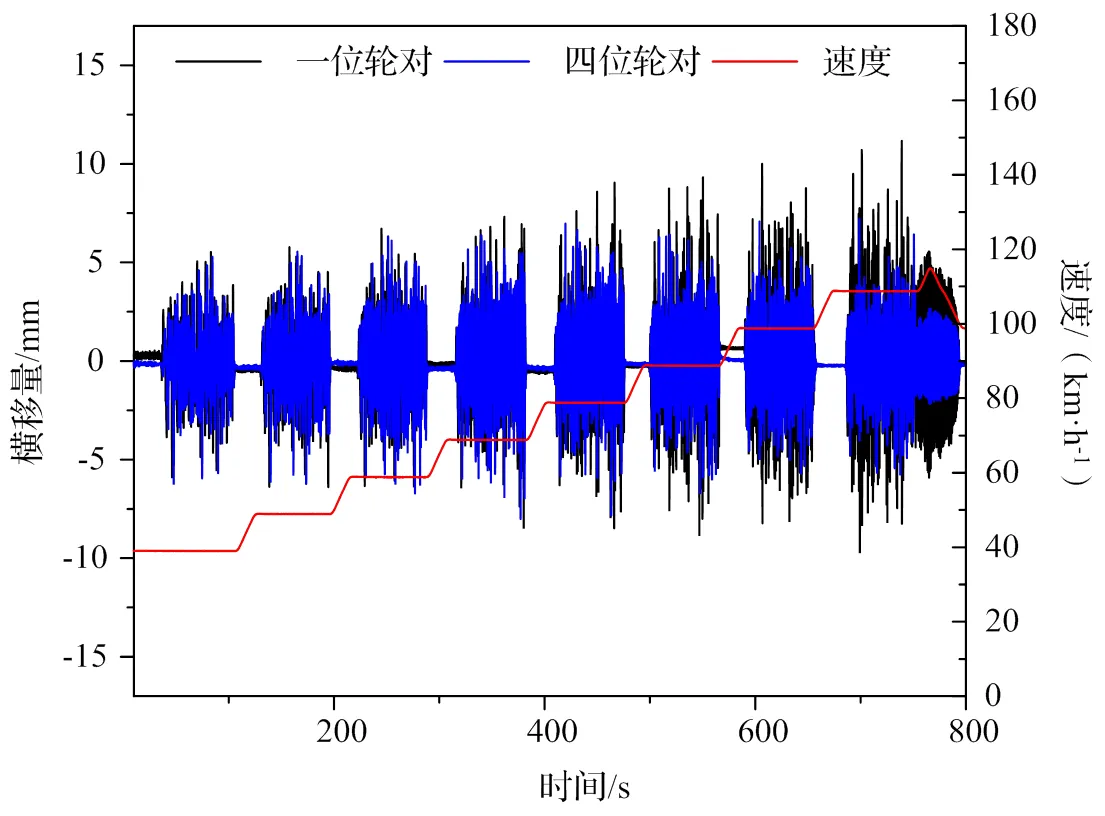
图10 全车空簧失气轮对横移量（试验）

3.2 垂向平稳性

由于全车空簧失气工况在速度为110 km/h时就出现轮对蛇行失稳现象，故滚振试验速度不再继续增加，原车正常工况以及全车空簧失气工况的垂向平稳性的试验计算结果如图11所示。当全车空簧发生漏气时，车辆的垂向平稳性指标明显变差，且在运行速度高于80 km/h时就超过2.5（优级）的限值，对乘客的乘坐舒适度有较大的影响；随着运行速度的增加，其垂向平稳性指标整体也呈现增大的趋势，不过正常工况下车辆在试验速度范围内的垂向平稳性指标均为优级，能够满足该地铁车辆正常运行速度下的乘坐性能要求。

图11 垂向平稳性对比（试验）

4 结论

动力学仿真计算以及滚振试验具有线路试验所不具备的条件和优势，如设置高速运行等极限运行工况（探索非线性临界速度）、进行悬挂元件故障试验等恶劣工况等。动力学仿真较其他两种方法能够极其方便地对各种参数进行修改优化分析，得到规律性结果为滚振试验以及线路试验提供一定的理论基础；滚振台滚振试验较线路试验的成本更低，试验条件与线路试验相接近并且对于某些运行工况也更加安全，能模拟线路运行工况的动态环境，对于车辆研制过程中的中间调试，改善和优化车辆的性能，发挥着越来越重要的作用。

通过对比动力学仿真计算结果与滚振试验结果，由于滚振试验与动力学仿真的运行条件有些许差异并且动力学计算仿真中对一些次要因素进行了假定和简化，所以计算结果与试验数据并不能完全符合，但是两者关于运行稳定性和垂向平稳性的规律都是相似的，通过分析其规律能够得出以下结论：

（1）该A型地铁转向架具有足够的蛇行运行稳定性以及优秀的垂向平稳性，能够满足最高运行速度120 km/h的设计要求，为线路试验提供了一定的参考价值，该转向架性能优异，达到了开发目标；

（2）全车空簧失气后，车辆非线性临界速度大幅度降低，安全性指标（轮轴横向力、轮轨垂向力、脱轨系数、轮重减载率）有所增加，其垂向平稳性指标较原车正常工况明显增大，并且运行速度越高差距越大，若车辆在运行过程中出现全车空簧失气现象，应立即降低车辆运行速度，为保证运行品质，建议限速80 km/h。

[1]张淑梅.河北造首列石家庄1号线A型地铁在唐山启运交付[EB/OL]. （2016-04-12）.http://ts.hebnews.cn/2016-03/28/content_5419019.htm.

[2]黄运华，李芾，傅茂海，等. 120km/h B型地铁车辆动力学性能研究[J]. 机车电传动，2009（5）：27-29，43.

[3]李晨，曾京. 某B型地铁列车转向架构架强度分析[J]. 机械，2020，47（8）：31-36.

[4]张传英. 空气弹簧附加气室对车体振动行为的影响研究[J]. 机械，2019，46（9）：41-45.

[5]李龙. 高速车辆运动稳定性的研究[D]. 成都：西南交通大学，2011.

[6]张雪锋. 铁道车辆悬挂系统分岔动力学及半主动控制的研究[D]. 石家庄：石家庄铁道大学/石家庄铁道学院，2003.

[7]李朝曦，傅茂海，邹纪操，等. 空气弹簧失效对地铁车辆动力学性能的影响[J]. 机械工程与自动化，2018（6）：30-33.

[8]吴兴文，池茂儒，朱旻昊，等. 空气弹簧模型对铁道车辆动力学性能的影响[J]. 交通运输工程学报，2013，13（2）：54-59.

[9]国家标准化管理委员会. 机车车辆动力学性能评定及试验鉴定规范：GB/T 5599－2019[S].

[10]中国铁路总公司. 高速动车组整车试验规范：TJCL007-2008[S]. 北京：中国铁道科学研究院，2008.

[11]Testing and approval of railway vehicle from the point of view of their dynamic behaviour-Safety-Track fatigue-Ride quality：UIC-518 [S]. 2005.

[12]高浩，罗仁，池茂儒，等. 车辆系统空气弹簧失气安全性分析[J]. 交通运输工程学报，2012，12（3）：60-66.

[13]丁奥，王勇，吴佳佳，等. 基于SIMPACK的铁道车辆曲线通过能力研究[J]. 机械，2019，46（4）：37-41.

Dynamic Simulation and Rolling Vibration Test for the Performance of Type A Subway Bogie

FAN Qingyu1，CHI Maoru1，LIANG Shulin1，SONG Yu2，YU Mingyang2，WANG Huansheng1

(1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 2.Beijing Subway Rolling Stock Equipment Co., Ltd., Beijing 100079, China)

In this paper, a dynamic model of the 120 km/h type A metro bogie is established and relevant dynamic performance indexes are calculated. The bogie design is analyzed. Based on the dynamic simulation results, the rolling vibration test of the bogie is further carried out on the roller rig. Suggestions are given for vehicle operation under the condition of air loss fault of air spring. The simulation calculation and test results show that the type A metro has good hunting stability, and its stability reaches the premium standard when running at a speed of 40~120 km/h on the U.S. V-class straight line. Both critical speed and operation stability meets the requirements of the maximum operation speed of 120 km/h on the rail line, which provides theoretical basis and test reference for the bogie to run on the track. After the air spring loses air, the nonlinear critical speed of the vehicle is greatly reduced, the safe index (lateral force, vertical force, derailment coefficient, and rate of wheel load reduction) is increased, and the vertical stability index is obviously increased compared with the normal working condition. The higher the running speed, the bigger the difference. If air loss fault of air spring occurs in the running process, the running speed should be reduced and limited to 80 km/h in order to ensure the running quality.

Type A subway bogie；hunting；dynamic performance；rolling vibration test

U270.1+1

A

10.3969/j.issn.1006-0316.2021.06.005

1006-0316 (2021) 06-0027-08

2020-11-09

中国-拉共体轨道交通联合实验室项目（KY201701001）

樊庆宇（1997－），男，山东冠县人，硕士研究生，主要研究方向为车辆系统动力学，E-mail：1361666799@qq.com；池茂儒（1973－），男，四川通江人，研究员，博士生导师，主要研究方向为铁道车辆系统动力学、空轨车辆设计理论、悬浮车辆振动与控制；梁树林（1967－），男，山西盂县人，教授级高级工程师，硕士生导师，主要研究方向为车辆工程结构可靠性及动力学、车辆系统故障诊断及智能运维。