框架-核心筒结构框架剪力调整方法研究
陈才华, 王翠坤, 潘玉华, 熊羽豪, 潘从建
(1 中国建筑科学研究院有限公司, 北京 100013; 2 国家建筑工程技术研究中心, 北京 100013)
0 引言
对于框架-核心筒结构,小震作用下结构总体处于弹性状态,框架与核心筒各自分担的剪力基于双重体系协同工作的原理由其相对刚度决定。核心筒刚度大,承担了绝大部分的剪力,是抗震的第一道防线,在中、大震作用下连梁先进入塑性导致核心筒整体刚度下降,框架与核心筒的相对刚度提高导致内力重分布,一部分地震力从核心筒转至框架,因此框架作为抗震的第二道防线,需要具备一定的强度(承载力),保证能承接从核心筒转移的地震力。
中美设计规范都对框架的地震剪力提出了调整的规定。美国规范采用规定外框承担最小剪力的方法,简称为“25%规定”。美国规范IBC2000[1]和ASCE 7-05[2]中规定:在双重抗侧力体系的框架-核心筒(框架-剪力墙)结构中,地震作用下,框架部分的设计层剪力不小于该层总剪力的25%。美国规范UBC1997[3]中对双重抗侧力框剪结构规定:框架应能独立承担底部设计剪力的25%。中国规范采用规定最小框剪比的方法,对计算所得的按弹性刚度分配的框架内力进行放大,简称“0.2Q0调整”。《建筑抗震设计规范》( GB 50011—2010)[4]、《高层建筑混凝土结构技术规程》(JGJ 3—2010)[5]规定:框架部分分配的楼层剪力最大值不宜小于底部总剪力的10%;当框架部分分配的楼层剪力最大值小于底部总剪力的10%时,应将其调整至底部总剪力的15%;当框架部分分配的楼层剪力最大值小于底部总剪力的10%但不大于20%时,应按底部总剪力的20%和框架部分楼层剪力最大值的1.5倍二者的较小值进行调整。
框架设计剪力的差异会导致按中美规范设计的外框截面、整体结构性能均存在一定的差异,很多学者也开展了相关的对比研究[6-10]。本文通过设计4个不同框剪比的框架-核心筒模型,对现行中美规范的框架剪力调整方法进行了对比分析。通过大震弹塑性时程分析得到大震下框架分担剪力的变化规律,提出适用于框架-核心筒结构的框架设计剪力调整策略,并给出实用的调整方法建议。
1 研究模型
1.1 模型设计
建立典型的框架-核心筒结构模型,并在整体抗侧刚度接近的前提下调整框架和核心筒的相对刚度,从而得到不同框剪比的框架-核心筒模型。三维模型如图1所示,共46层,首层层高6m,2,3层层高5.5m,4层层高5m,其余楼层层高4.2m,总高198.4m;平面布置如图2所示,平面尺寸45m×45m,核心筒尺寸21m×21m;外框由型钢混凝土柱和钢梁组成,内筒采用混凝土核心筒;核心筒(包括连梁)和框架柱混凝土采用C60(1~21层)、C50(22~36层)和C40(37~46层),楼板混凝土采用C30,钢材采用Q345,钢筋采用HRB400;标准层板厚120mm,楼面附加恒荷载2.5kN/m2,活荷载2kN/m2,框架梁线荷载(幕墙荷载)6kN/m;地震作用按7度(0.15g)设防,场地类别Ⅱ类,地震分组第一组。

图1 三维模型

图2 平面布置
通过改变连梁高度和框架梁高度以及适当调整墙厚及柱截面,设计了4个总体抗侧刚度接近、但框架与核心筒相对刚度不同的计算模型(编号为A1~A4),各模型的具体的截面信息见表1~4。
1.2 主要计算指标
采用PKPM(V4.1)软件进行弹性分析和设计。各模型主要计算指标见表5,层间位移角曲线和框剪比分布曲线分别见图3、图4。可以看出,模型A1~A4的周期和最大层间位移角等指标接近,表明整体刚度接近;最大框剪比分别为5.3%,10.4%,15.3%,20.0%,符合前述模型设计的原则。

图3 各模型层间位移角曲线

图4 各模型框剪比曲线
2 中美规范剪力调整比较
对模型A1~A4,分别按中美规范规定对框架剪力进行内力调整得到相应的框剪比曲线,并和小震下的框剪比曲线对比(图5)。可知,按中国规范、美国规范的调整后的框架剪力差异较大。中国规范是将全楼的框架剪力调整至相同的大小,而美国规范则是近似三角形分布,结构底部大,越到上部越小;从具体数值看,按美国规范调整后中下部的框架剪力更大,而按中国规范调整后的中上部框架剪力更大。
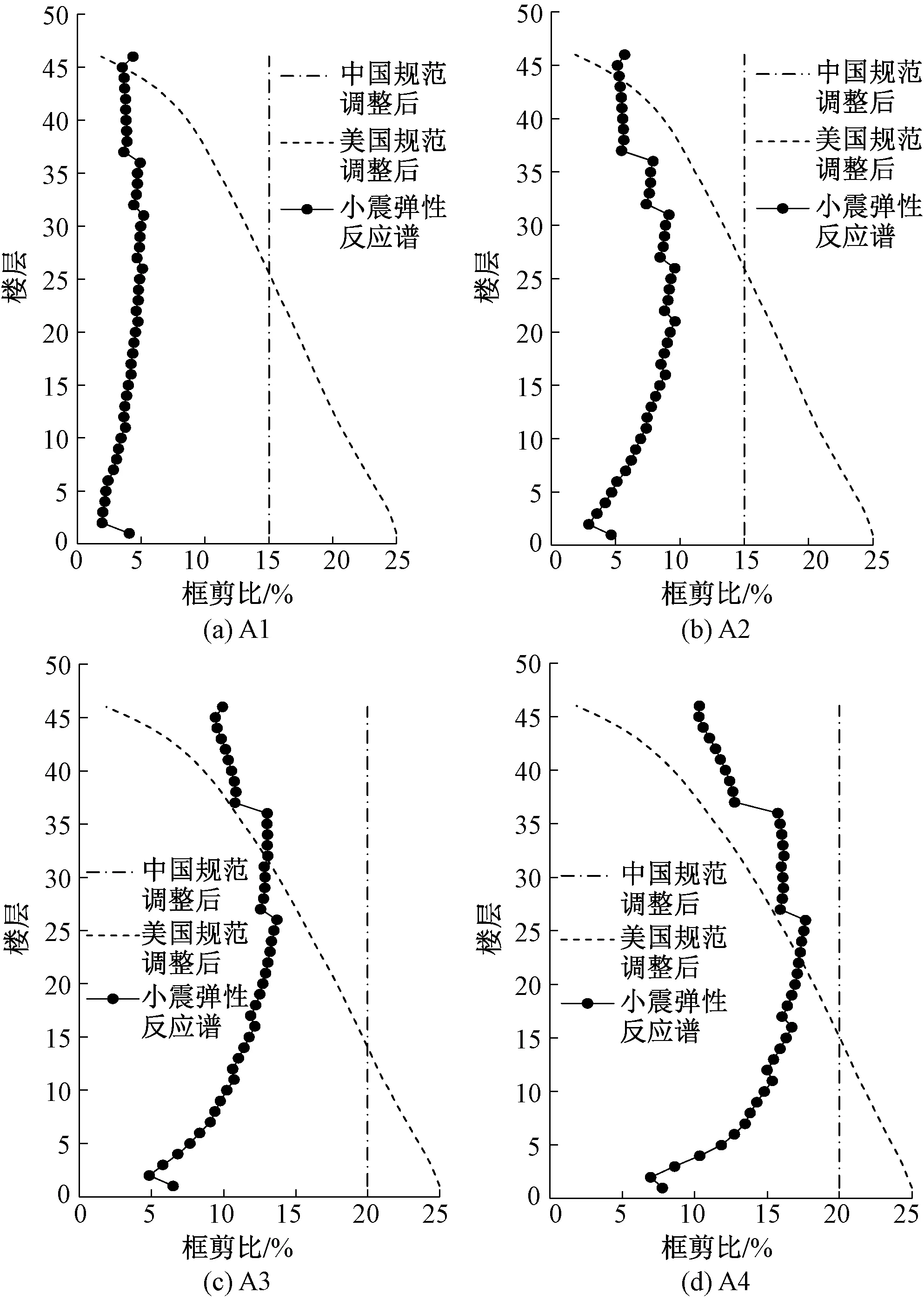
图5 各模型框架剪力调整

模型A1截面及参数/mm 表1

模型A2截面及参数/mm 表2

模型A3截面及参数/mm 表3
结合弹性分析时按刚度分配的框架剪力比,可以得到4个模型各楼层的框架剪力放大系数(图6),中国规范的放大系数曲线呈中间小两头大,而美国规范的放大系数曲线越往下越大。对于模型A1,26层及以上中国规范的放大系数大于美国规范,最大差异为4.25∶1.01(45层);25层及以下美国规范的放大系数大于中国规范,最大差异为12.78∶7.75(2层)。对于模型A2,26层及以上中国规范的放大系数大于美国规范,最大差异为2.92∶1.00(45层);25层及以下美国规范的放大系数大于中国规范,最大差异为8.54∶5.18(2层)。对于模型A3,15层及以上中国规范的放大系数大于美国规范,最大差异为2.12∶1.00(45层);14层及以下美国规范的放大系数大于中国规范,最大差异为5.11∶4.13(2层)。对于模型A4,16层及以上中国规范的放大系数大于美国规范,最大差异为1.94∶1.00(45层);15层及以下美国规范的放大系数大于中国规范,最大差异为3.55∶2.87(2层)。由图6可知,在结构中下部,中国规范的框架剪力放大系数低于美国规范;在结构中上部,中国规范的框架剪力放大系数高于美国规范;且外框相对刚度越小(框剪比越小)的模型,二者的差异越大。

模型A4截面及参数/mm 表4

各模型主要指标 表5

图6 各模型框架剪力放大系数
3 动力弹塑性分析
在对4个模型进行性能化设计后得到配筋,利用ABAQUS软件进行动力弹塑性分析。核心筒墙肢和框架柱的性能目标为抗弯中震不屈服、抗剪中震弹性,大震满足抗剪截面限制条件;设计时不考虑二道防线的框架剪力调整。
3.1 动力时程分析地震输入
动力弹塑性分析时选取了10条地震波进行单向输入,峰值加速度为310gal,对应7度(0.15g)大震。地震波包含了3条人工波(RGB01,RGB02,RGB03)和7条天然波(S0004,S0010,S0013,S0055,S0072,S0073,S0095),其波形和对应的频谱见图7。每条地震波时程分析得到各模型的基底剪力与反应谱法计算结果的对比见表6,各模型在10条波作用下基底剪力平均值与反应谱法计算结果的比值在103%~107%之间。

各条波基底剪力与反应谱分析结果对比 表6

图7 地震波波形及频谱
3.2 大震下框剪比
在结构动力时程分析中,随着结构进入塑性,内力会在核心筒和框架之间重分布,框剪比的变化可以反映二者相对刚度的变化。不同时程波作用下的框剪比曲线不相同,模型A1~A4在10条地震波作用下的楼层框剪比曲线如图8所示。由于10条波下的结果存在一定的离散性,为了对比不同模型的差异,作出各模型在10条地震波作用下的楼层平均框剪比曲线见图9,模型A1~A4楼层平均框剪比的最大值分别为8.2%,16.9%,23.5%,29.6%。
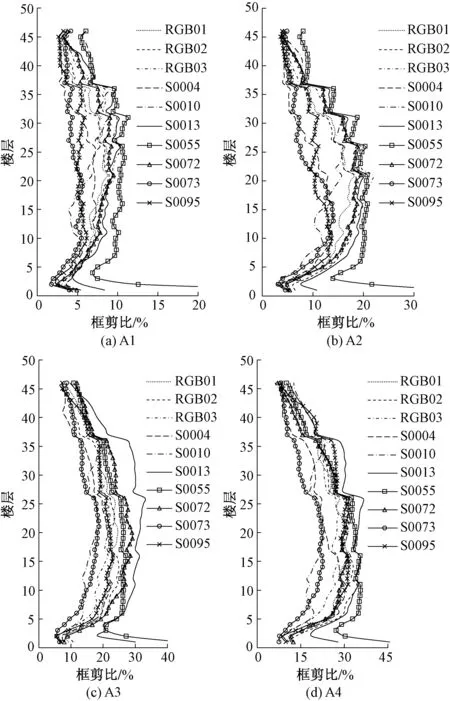
图8 各模型框剪比曲线

图9 各模型楼层平均框剪比曲线
3.3 框架剪力对比
图10比较了4个模型在小震、大震下框架分担的剪力和按中美规范调整的情况。可以看到,对于外框刚度较小的模型A1(弹性分析时最大框剪比5%),大震弹塑性下框架分担的剪力比例远小于中美规范调整后的数值;对于模型A2(弹性分析时最大框剪比10%),大震弹塑性下框架分担的剪力在结构中上部更接近美国规范的调整后数值,在中下部更接近中国规范的调整后数值,但超出了0.15V0,未超出美国规范的调整后数值;对于模型A3(弹性分析时最大框剪比15%),大震弹塑性下框架分担的剪力除底部10层外均显著高于美国规范的调整后数值,中部20层均超出中国规范的调整后数值;而对于外框刚度较大的模型A4(弹性分析时最大框剪比20%),大震弹塑性下框架分担的剪力除底部5层外均显著高于美国规范调整后数值,除顶部及底部少量楼层外,也明显高于中国规范调整后数值。总体而言,对于外框刚度较小的模型,按规范调整放大后框架设计剪力大于实际分担剪力,而对于外框刚度较大的模型,按规范调整后的部分楼层的框架设计剪力低于其实际分担剪力。

图10 各模型框架小震、大震下分担剪力与规范调整值对比
现行设计规范基于抗震概念的二道防线剪力调整,在基于小震弹性的抗震设计体系下,避免了繁杂的结构弹塑性分析,尤其是在结构分析软硬件均不能满足结构设计需要的客观条件下,对提高结构抗震安全性发挥了重要作用;但无论中国规范的“0.2Q0”调整还是美国规范的“25%规定”,均属于概念性和主观经验性的规定,并没有定量的数据支撑。随着建筑结构弹塑性分析的发展应用,直接从结构受力原理和大震下的塑性发展导致的内力重分布规律出发,探寻符合二道防线要求的框架剪力调整策略,可以使结构设计更加科学合理。
4 剪力调整方法建议
通过对结构进行大震弹塑性分析,可以了解结构的塑性发展过程和最终的塑性损伤状态,得到结构从弹性到弹塑性发展过程中的内力重分布,从而对小震弹性设计的框架剪力进行调整。本文提出以下两种框架剪力调整建议方法:
(1)基于弹塑性时程分析的调整系数方法
根据《建筑抗震设计规范》(GB 50011—2010)[4]、《高层建筑混凝土结构技术规程》(JGJ 3—2010)[5]规定,选择符合规范要求的3条地震波或7条地震波,通过大震弹塑性时程分析计算得到各楼层大震下的框剪比,然后除以小震弹性时的框剪比,从而得到各楼层的框架剪力调整系数。对于3条地震波,应取调整系数的包络值;对于7条地震波,可取调整系数的平均值。
(2)基于等效线性化的调整系数方法
弹塑性时程分析方法存在地震输入和计算分析工作量大两个问题,因此借鉴性能化设计的思路,提出等效线性化的方法。核心筒剪力墙作为抗震的第一道防线承担了大部分的剪力,随着地震输入强度的增加最先进入塑性,其损伤主要集中在连梁,因此可以通过折减连梁刚度采用反应谱方法实现结构大震下的等效线性化分析,得到各楼层的框剪比,然后除以小震弹性时的框剪比,从而得到各楼层的框架剪力调整系数。
等效线性化调整系数方法采用传统的反应谱分析,计算简便且与现行的性能化方法一致,实用性好,其关键在于如何确定连梁刚度折减系数。以模型A1~A4作为案例,对连梁刚度折减系数进行研究,得到不同刚度折减系数下的框剪比曲线,并与大震弹塑性分析得到的框剪比曲线对比,见图11。从图中可以看出,随着连梁刚度系数减小,框架相对核心筒的刚度增加,框剪比曲线外扩,对模型A1~A4,大震弹塑性分析的框剪比曲线总体上均介于连梁刚度系数为0.08和0.1的等效线性化分析结果之间,即连梁刚度折减系数可取0.08~0.1。

图11 各模型基于等效线性化的框架剪力调整对比
5 结论
本文基于整体刚度相近的原则设计了4个不同框剪比的框架-核心筒模型,对比了现行中美规范的框架剪力调整方法差异,并通过大震弹塑性时程分析得到大震下框架实际分担剪力,并与规范调整后的结果进行比较,得到主要结论如下:
(1)动力时程分析表明,大震下框架-核心筒结构发生内力重分布,其框架应具备一定的强度(承载力),保证能承接从核心筒转移的地震力,实现抗震二道防线作用。
(2)在结构中下部,中国规范的框架剪力放大系数低于美国规范;在结构中上部,中国规范的框架剪力放大系数高于美国规范。
(3)对于外框刚度较小的模型,按规范调整后放大后框架设计剪力大于大震下实际分担剪力;而对于外框刚度较大的模型,按规范调整后的部分楼层的框架设计剪力低于大震下其实际分担剪力。
(4)根据结构大震下的塑性发展导致的内力重分布规律,分别基于弹塑性时程分析和等效线性化分析提出了两种实用的框架剪力调整方法,可供设计参考。

