FKM标准在制动夹钳单元疲劳强度评估中的应用

孟永帅 曾梁彬 王起梁 赵金良 刘 超

(中车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011)

0 引言

制动夹钳单元作为列车基础制动装置的执行机构，其结构的可靠性直接影响到列车运行的安全性[1]，因此在结构设计时需要对其疲劳性能进行评估。目前铁路技术发达国家均制定了相关标准来规范疲劳强度的评估方法，如我国的《铁道机车车辆强度设计及试验鉴定规范》、欧洲的《铁路应用—铁道车辆车体结构的强度要求》、日本的《车辆用转向架构架设计通过规则》以及国际铁路联盟试验研究中心的研究报告ORE B12/RP17等[2]。

目前在进行疲劳强度评估时采用较多的是国际铁路联盟试验研究中心研究报告ORE B12/RP17中的方法，该方法通过应力投影将多轴应力转化为单轴应力，再根据构件的修正Goodman曲线进行疲劳强度评估[2]，由于该方法计算过程相对简单，因此在铁路行业使用范围较广，但该方法在评估中未考虑结构设计、制造、载荷等因素的影响。

下文采用德国机械工程研究委员会编制的FKM标准中的评估方法对制动夹钳单元的进行疲劳强度评估，并和传统的修正Goodman疲劳曲线强度评估结果对比分析，探索新的疲劳强度评估方法在轨道交通结构强度校核中的应用。

1 制动夹钳单元结构

某制动夹钳单元结构如图1所示，主要由制动缸、球关节、吊架、杠杆、销轴、闸片托以及闸片拖吊等零部件组成，制动夹钳单元通过闸片拖吊螺栓和吊架橡胶球关节安装在转向架上。

制动时，通过向制动缸内充气使制动缸推动杠杆向外运动，杠杆绕销轴转动，带动闸片托向内运动夹紧制动盘，闸片摩擦块和制动盘间发生摩擦耗能，从而实现列车的制动。

2 FKM标准简介

FKM标准是德国机械工程研究委员会基于TGL标准、DIN18800、VDI2226、DIN4113-2、DIN 743、DIN EN 1999等标准以及FKM研究报告编制而成，主要用于评估钢、铸铁和铝材料结构的静强度和疲劳强度。在评估过程中考虑了大多数对构件强度(静态和动态)产生影响的因素，如表面粗糙度、工作温度、残余应力、结构细节、载荷情况等[3-4]。

标准采用名义应力法和局部应力法两种方法对构件的静强度和疲劳强度进行评估(见图2)。两种方法的评估过程基本相同，名义应力法主要适用于杆状或者壳构件，局部应力法适用于各种构件[3]。

图2 FKM标准强度评估方法

文中制动夹钳单元的应力通过有限元模拟仿真获得，因此选择标准中的局部应力法进行疲劳强度评估，其评估过程如图3所示。

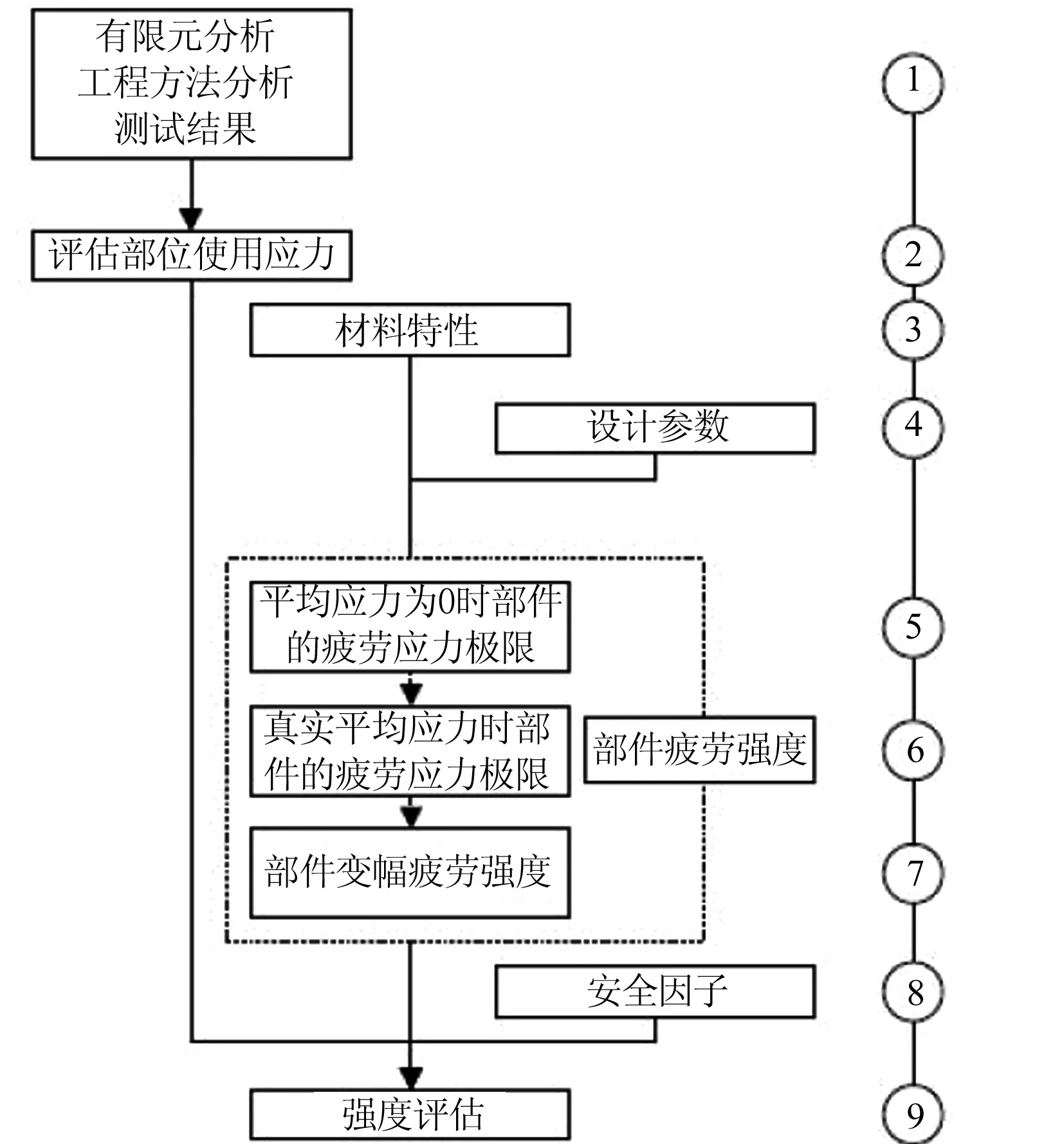
图3 局部应力法疲劳强度评估

3 制动夹钳单元仿真模型校核

在有限元软件中建立仿真模型，为保证计算结果准确性，根据ASME V&V标准对仿真模型进行校核、确认[5]。首先校核仿真模型的稳定性，采用不同尺寸网格进行计算，对模型中某些节点(见图4)的应力运用J.R.Beisheim提出的方法进行校核[6]，校核结果表明3种网格尺寸的计算结果相差很小，如表1所示，模型具有较好的稳定性。

图4 模型校核点位置图

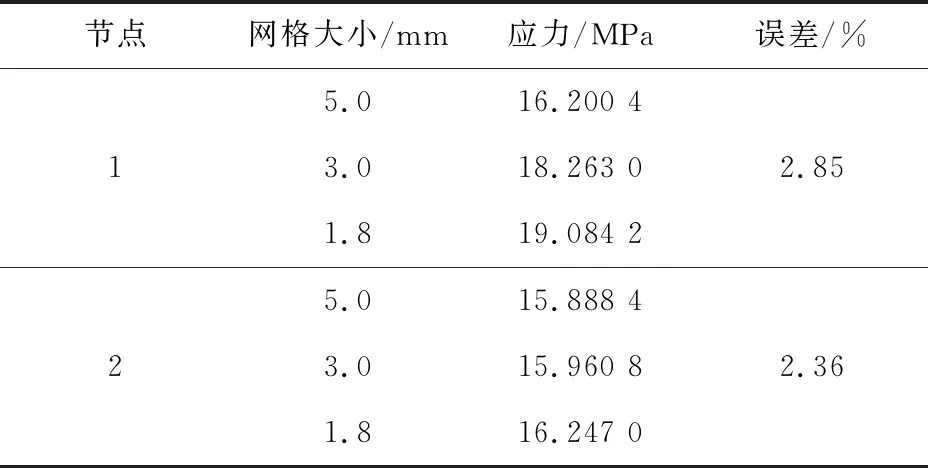
表1 仿真模型校核结果

为验证仿真模型的准确性，根据应力测试结果和ASME V&V标准，对仿真模型进行确认，结果表明，节点1和节点2的值分别为6.3%和7.6%，满足标准要求(不大于10%)[5]，因此判定仿真模型具有较好的准确性，可以用于疲劳强度的评估分析。

图5 制动夹钳单元静强度测试

有限元仿真模型校核确认后，采用1.8 mm网格模型对制动夹钳单元的疲劳工况进行仿真计算。

4 吊架结构的疲劳强度评估

4.1 基于FKM标准的疲劳评估

取吊架的最大应力点作为危险评估点，评估点的应力值如表2所示。

表2 评估点应力值 /MPa

吊架材料为QT600，对应FKM标准中的EN-GJS-600[3]，根据标准及设计参数，计算得到材料的抗拉强度Rm为600 MPa，疲劳极限σw为204 MPa。

由于夹钳单元在常温环境下工作，因此在评估中不考虑高温影响。

FKM标准通过设计系数KWK,σ来考虑疲劳缺口系数、粗糙度系数等因素对疲劳强度的影响。

(1)

按公式(1)对评估点各应力设计系数进行计算，计算过程及结果如表3所示。

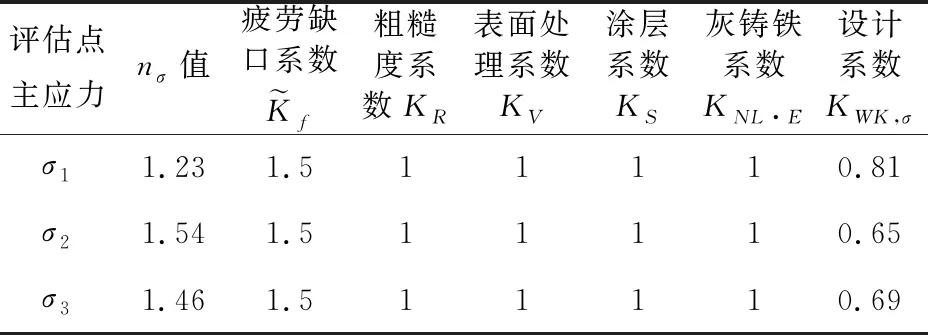
表3 评估点各应力设计系数

为考虑载荷类型对构件疲劳强度的影响，标准利用设计系数KWK，σ、平均应力系数KAK、变幅疲劳系数KBK等计算疲劳强度幅值σBK，同时考虑各应力分量疲劳强度的限值[3]。

(2)

利用公式(2)得到吊架评估点各主应力的疲劳强度幅值σBK(见表4)。

表4 各主应力疲劳强度幅值

根据制动夹钳单元的使用情况，确定吊架的安全系数jD为1.35[3]。

FKM标准通过利用度来评估疲劳强度，当利用度小于等于1时，构件满足疲劳强度要求。利用度分为单独应力利用度αBK,σ和组合应力利用度αBK,σv，其计算公式为：

(3)

根据吊架的疲劳应力幅值、疲劳强度及安全系数，按公式(3)进行疲劳强度评估，其组合应力利用度为0.542，表明吊架满足疲劳强度要求。

则基于FKM标准的疲劳强度因子[7]为：

SFKM=1/σBK，v=1/0.542=1.85

4.2 基于修正Goodman曲线的疲劳评估

根据ORE B12/RP17报告中给出的修正Goodman曲线疲劳评估方法，首先对评估点各主应力进行应力投影，将多轴状态应力转化为单轴状态应力。

通过投影得到评估点的最大、最小主应力为：σmax=163.7 MPa，σmin=0。

(4)

按公式(4)得到评估点的平均应力和应力幅值分别为81.9 MPa、81.9 MPa。

吊架的材料性能为σb=600 MPa，σs=370 MPa，σ-1=249 MPa[8-9]。

根据评估点的平均应力和应力幅值，应用Smith图形式的修正Goodman曲线进行疲劳强度评估，评估结果如图6所示，从图中可以看出，评估点在曲线范围内，满足疲劳强度要求。

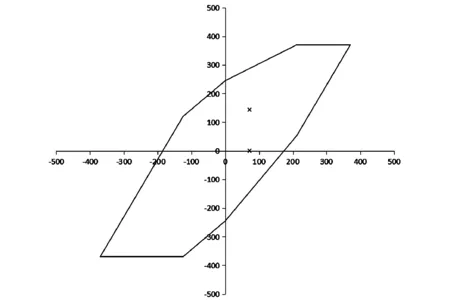
图6 Goodman曲线评估结果

则基于修正Goodman曲线的疲劳强度因子[10]如下：

4.3 两种评估结果对比分析

从FKM标准和Goodman方法的评估结果可以看出，两种方法的评估结果基本一致，都可判定吊架满足疲劳强度要求，说明FKM标准方法能够用于疲劳强度的评估。同时FKM标准的疲劳强度因子(1.85)小于Goodman方法的疲劳强度因子(2.15)，说明FKM标准评估相对保守，结果更加可靠，且评估过程中考虑了结构设计、载荷类型等多种疲劳影响因素，因此较为科学可靠。

5 结论

本文首先利用ASME V&V标准对某制动夹钳单元的有限元仿真模型进行校核、确认，保证了仿真模型的可靠性。在此基础上，采用FKM标准中的局部应力法对制动夹钳单元吊架进行疲劳强度评估，其危险点的组合利用度为0.542，满足疲劳强度设计要求。同时和基于修正Goodman曲线的疲劳评估结果进行了对比，结果表明：FKM标准的评估结果较为安全可靠，且评估过程中考虑了较多的疲劳影响因素，过程较为科学合理，在轨道交通结构的强度评估中具有较高的应用价值。