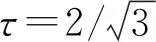自旋-1角动量分量的不确定关系
南 华, 玄东平, 胡晓会
(延边大学 理学院数学系, 吉林 延吉 133002)
1 引言与预备知识
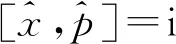
对于两个可观测量A和B, Robertson[4]推导出不等式
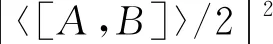
(1)

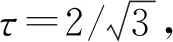
2 乘积形式的不确定关系
自旋角动量是量子系统的可观测量, 已知自旋-1角动量的三个分量为
且满足与轨道角动量相同的对易关系:
[Sx,Sy]=iħSz, [Sy,Sz]=iħSx, [Sz,Sx]=iħSy.
(2)
令ħ=1, 由不确定关系(1)可得
ΔSxΔSy≥|〈Sz〉|/2, ΔSyΔSz≥|〈Sx〉|/2, ΔSzΔSx≥|〈Sy〉|/2,
(3)
因此, 有
(ΔSxΔSyΔSz)2≥|〈Sx〉〈Sy〉〈Sz〉|/8.
(4)
由于式(4)仅在不等式两端全为0时等号成立, 但没有实际意义.因此考虑不确定关系
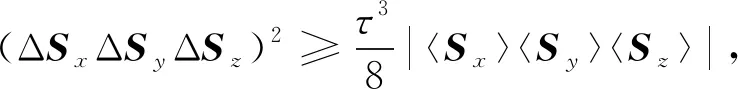
(5)
使式(5)等号成立的τ称为三方系数, 其作用是使式(5)在两端非零时可达到下确界, 即不确定关系(5)是紧的.
考虑系统纯态的一般形式
通过计算可得
为确定不等式(5)中常数τ的值, 根据
对于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得
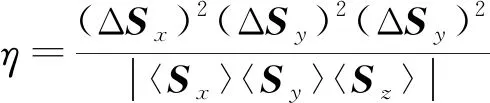
(6)
的最小值.可知当θ1=π/2,θ2=5π/4时, 存在π/5<α1<π/4, π/9<α2<π/8, 使得

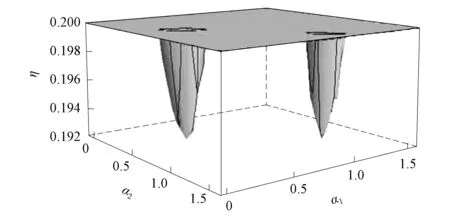
图1 式(6)最小值的数值解Fig.1 Numerical solution of minimum value of formula (6)
3 和式的不确定关系
下面研究自旋-1角动量的三个分量相关和式的不确定性关系.由式(2)可得
(ΔSx)2+(ΔSy)2≥2ΔSxΔSy≥|〈Sz〉|,
(ΔSy)2+(ΔSz)2≥|〈Sx〉|, (ΔSx)2+(ΔSz)2≥|〈Sy〉|.
(7)
由式(7)可得三个分量的和式不等式
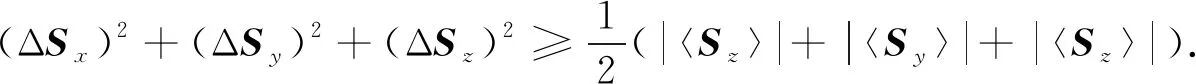
(8)
对于N维系统, 自旋-l时自旋量子数l=(N-1)/2, 且对任意量子态有
由于Sk(k=x,y,z)的期望值定义了一个向量, 其最大长度等于沿任意轴的极值特征值, 因此文献[16]给出了如下不等式
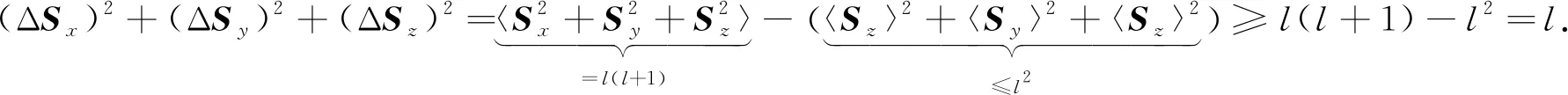
(9)
对一组数据{x1,x2,…,xn}, 已知代数平均值不超过二次平均值, 即
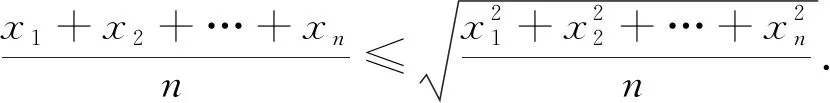
(10)
由此可得
由式(11)可知, 式(8)是非紧的, 因此考虑存在一个常数τ, 使不确定关系
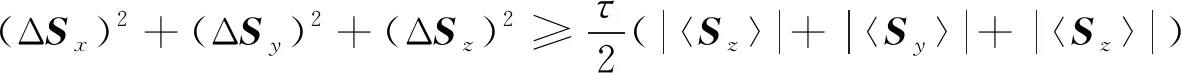
(12)
成为紧的, 即可达到该下确界.
对于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得
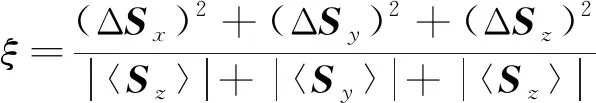
(13)
的最小值.
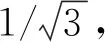
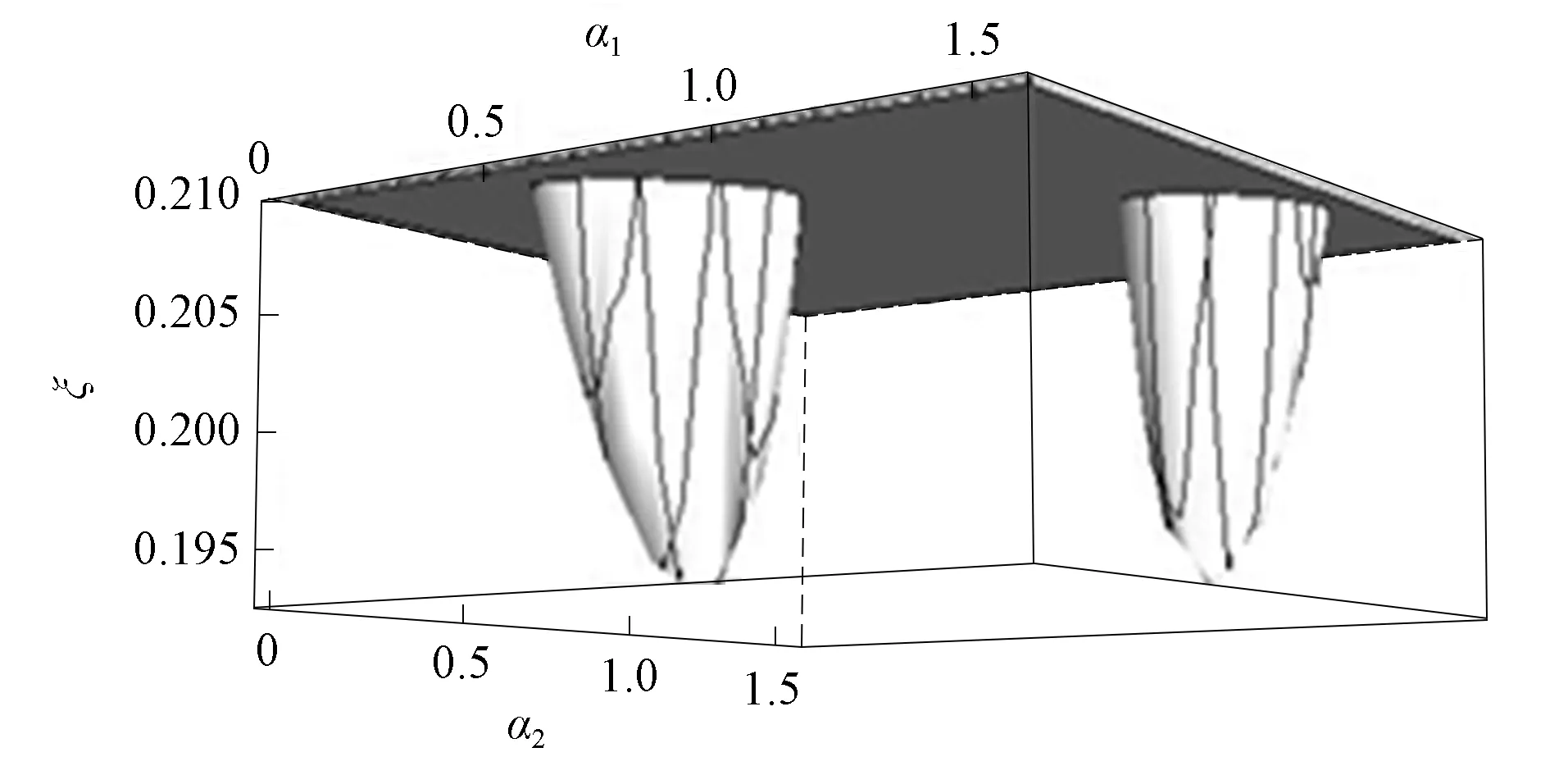
图2 式(13)最小值的数值解Fig.2 Numerical solution of minimum value of formula (13)