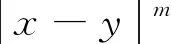加权Morrey空间上多线性奇异积分的振荡及变分算子的有界性
朱 敏, 陶双平
(西北师范大学 数学与统计学院, 兰州 730070)
1 引言与主要结果
设K(x,y)为Ω={(x,y)∈×:x≠y}上的连续函数, 满足
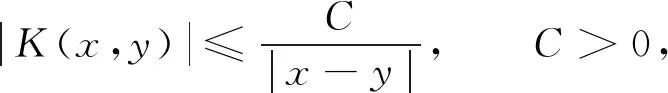
(1)
且对任意的x,x0,y∈, 当|x-y|>2|x-x0|时, 成立

(2)
其中0<β<1.满足条件(1)和条件(2)的K(x,y)称为标准的C-Z核.给定K(x,y)和局部可积函数b, 相应的算子和交换子分别定义为
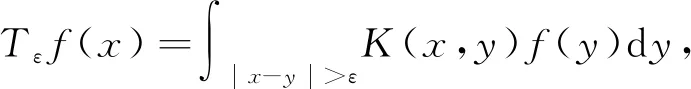
(3)

(4)
设{ti}是一列递减趋于0的正数序列, 文献[1]定义了相应于{Tε}的振荡算子:
相应于{Tε}的ρ-变分算子定义为
并记
由文献[2]知, O′(Tf)≤O(Tf)≤2O′(Tf).
Campbell等[3]证明了Hilbert变换的振荡和变分不等式在Lp(1 则有 记 Φ={β:β={εi},εi∈,εi0}. V(T)f(x)={Tεi+1f(x)-Tεf(x)}β=εi∈Φ. 因此, Vρ(T)f(x)=‖V(T)f(x)‖Fρ. 给定正整数m和上的m阶可微函数b, 用Rm+1表示b(x)在y点m阶展开的Taylor余项, 即 多线性奇异积分算子定义[4]为 (5) 设ω为局部可积函数, 1 则称ω∈Ap,q.一个局部可积函数b属于加权BMO空间是指 其中I为中的区间, 定义1[5]设1≤p<∞, 0 本文主要结果如下: 定理1设K(x,y)满足条件(1)和条件(2),ρ>2,T∶={Tε}ε>0和Tb∶={Tε,b}ε>0分别由式(3)和式(4)给出.若O(T)和Vρ(T)对于1 ‖O(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq),C>0, ‖Vρ(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq),C>0. ‖O(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq),C>0, ‖Vρ(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq),C>0. 引理1[9]对任意的区间I⊂, 若ω∈Ap,p≥1, 则存在一个常数C>0, 使得ω(2I)≤Cω(I), 进一步, 对于所有的λ>1, 有ω(λI)≤Cλpω(I), 其中C与I,λ无关, 且 引理3[1]对任意的区间I⊂, 若ω∈Δ2(满足双倍条件的函数集合), 则存在一个常数D>1, 使得ω(2I)≥Dω(I). 引理4[11]令b∈,b(m)∈Lq(), 则对任意的m∈和任意的p, 有 其中I(x,y)=(x-5|x-y|,x+5|x-y|). 引理5[5]令K(x,y)满足条件(1)和条件(2),ρ>2,T∶={Tε}ε>0和Tb∶={Tε,b}ε>0分别由式(3)和式(4)给出.若O(T)和Vρ(T)对于1 ‖O′(Tbf)‖Lq(ωq)≤C‖b‖BMO‖f‖Lp(ωp),C>0, ‖Vρ(Tbf)‖Lq(ωq)≤C‖b‖BMO‖f‖Lp(ωp),C>0. 由于O′(Tb)和Vρ(Tb)的证明类似, 因此本文只给出O′(Tb)的证明.对任意的区间I=(x0-l,x0+l)及任意的f∈Lp,k(ωp,ωq), 记f=f1+f2, 其中f1=fχ2I.则有 先估计I1.对于I1, 由引理5有 下面估计I2.由文献[1], 有‖{χ{ti+1<|x-y| 对于I3, 利用定义1、 权函数和BMO函数的性质及引理2, 有 下面估计I4.对于I4, 有 因此, I5≤C‖b‖BMO(ωp(2i+1I)(1-p′))1/p′=C‖b‖BMOω-1(2i+1I)=C‖b‖BMOωq(2i+1I)-1/q. 对于I6, 由文献[11]有|b2i+1I-bI|≤2(i+1)‖b‖BMO.因此, 由John-Nirenberg引理知, 存在正常数C1和C2, 使得对任意的I和α>0, 有 |{y∈I: |b(y)-bI|>α}|≤C1|I|exp{-C2α/‖b‖BMO}. 当b∈BMO时, 由引理2知, 对任意的δ>0, 有 ω({y∈I: |b(y)-bI|>α})≤Cω(I)exp{-C2αδ/‖b‖BMO}, 即 从而 因此, 更进一步, 有 |b2i+1I,ωp(1-p′)-bI,ωq|≤C(i+1)‖b‖BMO. 由引理3, 有 综合上述估计, 有 ‖O(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq),C>0. 定理1证毕. 对于任意的区间I=(x0-l,x0+l)及任意的f∈Lp,k(ωp,ωq), 记f=f1+f2同定理1的证明.对f1的估计同定理1.注意到 对于x∈I,k=1,2,…,m∈,y∈(2I)c, 有由文献[11]知, 对于任意的y, 有Rm+1(bk;x,y)=Rm+1(b;x,y).由文献[10]知, 当b∈BMO时, 有 因此, 有 与定理1的证明过程类似, 可得 ‖O′(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq), ‖Vρ(Tbf)‖Lq,kq/p(ωq)≤C‖b‖BMO‖f‖Lp,k(ωp,ωq). 定理2证毕.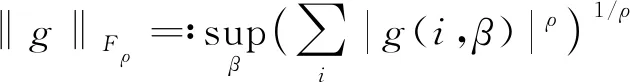
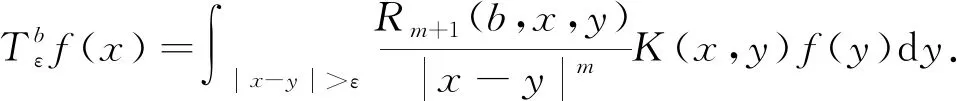
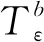

2 定理的证明

2.1 定理1的证明


2.2 定理2的证明