气象因素与急性闭角型青光眼发作关系的研究

李 柳，金 昱，刘 淼

（1.南昌市第一医院眼科，江西 南昌 330008；2.中山大学中山眼科中心南昌眼科医院，江西 南昌 330008）

急性闭角型青光眼（acute angle-closure glaucoma，AACG）是由于前房角突然关闭而造成眼压大幅度上升的眼部疾病[1]，发病时患者自觉剧烈眼痛，甚至恶心、呕吐，并有显著的视力障碍[2，3]。一般认为此病的诱因除情绪大幅度波动、极度疲劳外[4]，还与特定的气象条件相关[5]。气象因子可引起人体的内分泌系统转变，从而影响身体健康[6]。有科学研究报导气象因素与心血管疾病发病有关[7]。但目前国内外并无对气象因素与AACG 发病关联的研究。本研究通过对不同气象条件下AACG 就诊人次进行分析，探讨南昌市气象条件下AACG 发病特点与规律以及极端温度对AACG 发病的影响，建立南昌市AACG 逐月就诊人次数的预测模型，为AACG 病因学的探讨、诊治和预防提供参考。

1 资料与方法

1.1 一般资料 收集2015 年1 月1 日～2019 年10 月31 日在南昌市规模较大的综合性三级甲等医院门诊就诊的所有AACG 发病病例，AACG 诊断标准[8]：①视力骤降、有确定的发病时间；②眼压≥30 mmHg；③眼痛、头痛、畏光、流泪、部分患者恶心、呕吐等症状；④裂隙灯检查有睫状或混合充血；角膜和结膜水肿；前房较浅；瞳孔散大、变形或固定。搜集与AACG 就诊资料数据同步的气象资料，含日平均温度Ta（℃）、日最高温度Th（℃）、日最低温度Tl（℃）、日均值气压Pa（hpa）、日最大气压Ph（hpa）、日最小气压Pl（hpa）、日均值空气湿度Ha（%）、日最低湿度Hl（%）。以2015 年1 月1 日～2018 年10 月31 日（共46 个月）的数据用来拟合ARIMA 模型，2018 年11 月1 日～2019 年10 月31 日（共12 个月）的数据用于模型预测效果评价。

1.2 圆形分布计算流程 将12 个月转换成360°，1

天相当于0.9863°，以每月的月中值为组中值（αi）。按下列流程进行计算：①计算cosαi及sinαi的均值，分 别 以X 和Y 表 示。，fi为频数，n 为AACG 总人数；②计算角度离散程度指标γ 值；③计算平均角的正弦及余弦。，由上述结果推算值；④计算角离差S或S=；⑤检验方法为雷氏Z 值检验。Z=nγ2，Z＞Z0.05，表示有统计学意义。

1.3 建立ARIMA 模型 时间序列的特征分析及平稳化：建立时间序列，通过自相关系数函数图（Autocorrelationfunction，ACF）和偏自相关系数函数图（Partialautocorrelationfunction，PACF）分析序列的平稳性，因为ARIMA 模型只适用于平稳序列分析，非平稳序列需通过自然对数转换、一般差分或季节差分等方法进行处理。

1.3.1 模型识别和定阶 根据ACF 图、PACF 图和SPSS 23.0 软件初步拟合结果，定阶预先考虑使用ARIMA（p，d，q）或ARIMA（p，d，q）×（P，D，Q）模型，对模型参数从低阶到高阶进行逐项试验，根据文献资料[9]，该模型的阶数一般不超过2，因此可以在二阶以下逐一检验。

1.3.2 备选模型的参数估计和诊断 通过非线性最小二乘法估计参数，对模型的残差进行Ljung-BoxQ（白噪声）检验，以判定模型是否具有合理性。对各模型的AIC 和SBC 值进行综合比较。AIC 和SBC 值与模型的预测效果负相关。选择三个拟合优度统计量（AIC 和SBC）最小的模型为备选模型。

1.3.3 明确最优模型 用备选模型预测2018 年11 月1 日～2019 年10 月31 日（共12 个月）AACG 就诊人数，并与具体就诊人数进行对比，选择预测相对误差最小的模型为最优模型。

1.4 统计学方法 选用Excel 录入以上AACG 就诊资料及当期气象因素数据信息，选用SPSS 23.0 进行统计分析不同季节AACG 就诊率，采用圆分布方法分析AACG 就诊集中趋势，应用单因素相关分析及多元逐步回归分析8 项气象因素与AACG 就诊的关联性，建立ARIMA 模型，绘制相应的预测效果图。

2 结果

2.1 南昌市AACG 就诊集中趋势 2015 年1 月1日～2019 年10 月31 日记录的AACG 就诊人数显示，冬季发生AACG 的例数最多，见表1。

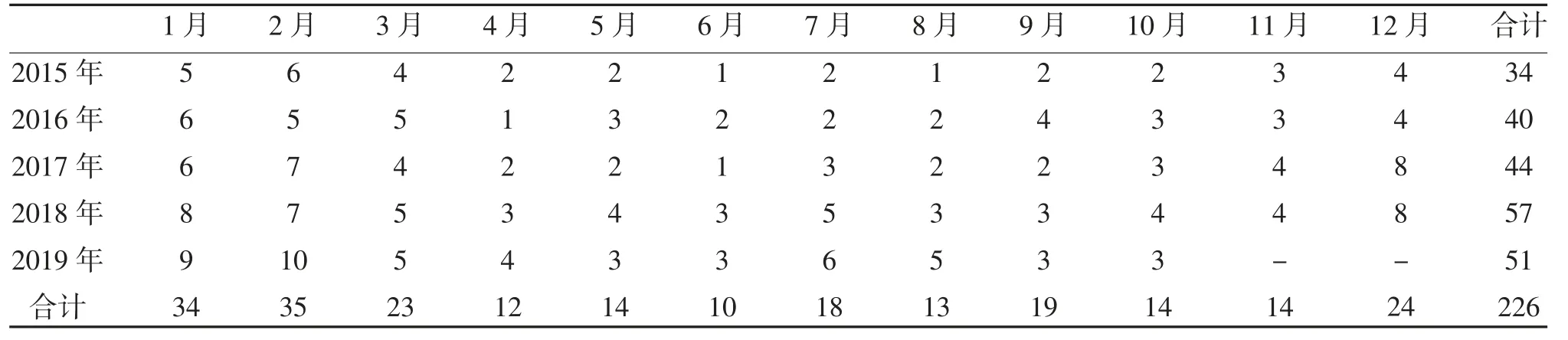
表1 各年度AACG 就诊人数月份分布情况（n）

2.2 气象因素与AACG 就诊人次数的关联性 将8项气象因素（Ta、Th、Tl、Pa、Ph、Pl、Ha、Hl）与AACG就诊人数分别进行单因素相关性分析，结果显示AACG 与Ta、Th、T1 呈负相关，与Pa、Ph、Pl、Ha、Hl呈正相关，见表2；多元逐步回归分析显示，Ta、Th、T1、Hl 与AACG 就诊人次数有关（P＜0.05），见表3。

表2 气象因子与AACG 就诊人次数的单因素相关性分析

表3 气象因素与AACG 就诊人次数的多元逐步回归分析

2.3 ARIMA 预测模型

2.3.1 南昌市AACG 发病趋势 依据2015 年1 月1日～2018 年10 月31 日南昌市AACG 就诊人数随时间的趋势分析，见图1，初步认为南昌市AACG 搜集病例的时间序列是非平稳曲线，每年12 月～次年2月为一个发病高峰，2017 年12 月～2018 年1 月就诊的病例较多，且呈显著的单峰分布。ACF 和PACF图均不截尾，但有拖尾，见图2，提示该时间序列为非平稳序列。

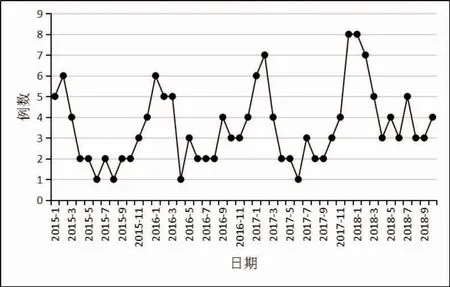
图1 AACG 就诊人数时间序列图

图2 AACG 就诊人数ACF 和PACF 函数图

2.3.2 序列的平稳化及模型识别 对2015 年1 月1日～2018 年10 月31 日南昌市AACG 数据信息进行自然对数转化和1 阶差分处理，获得差分后的ACF图和PACF 图，见图3。相关系数在滞后编号12 时尚未落入95%的置信区间内，初步说明需建立的最优ARIMA（p，d，q）或ARIMA（p，d，q）×（P，D，Q）模型将比较复杂。

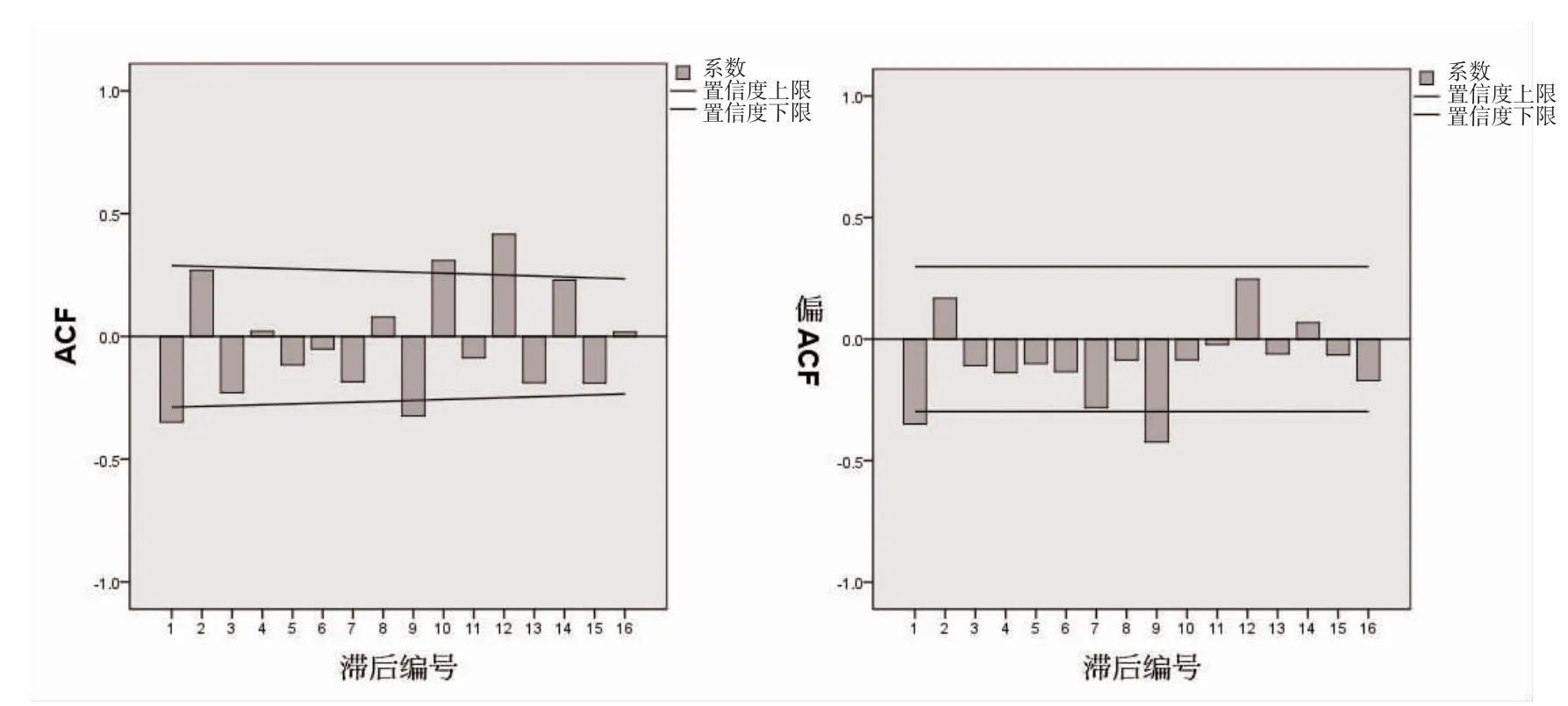
图3 AACG 就诊人数数经自然对数转化和1 阶差分处理后ACF 和PACF 函数图

2.3.3 模型的初步建立、确定 在满足模型简洁、各参数都有统计学意义（P＜0.05）和Ljung-BoxQ 统计量所对应的P＞0.05 的情况下，选择标准化BIC 最小（0.651）、平稳R2最大（0.658）、均方根误差较小（1.124）的ARIMA（1，0，0）（2，0，0）12模型，其Ljung-BoxQ=9.762，P=0.834，残差序列为白噪声。图4 显示，残差序列ACF、PACF 均落入置信区间内，表示模型信息提取较为充分，时间序列各项之间没有相关性。

图4 模型ARIMA（1，0，0）（2，0，0）12 残差序列ACF、PACF 函数图

2.3.4 模型预测分析 以2015 年1 月1 日～2018 年10 月31 日AACG 就诊人数时间序列拟合ARIMA（1，0，0）（2，0，0）12后，再以2018 年11 月1 日～2019年10 月31 日的数据为验证数据进行预测分析，根据预测值与实际值的相对误差判断模型的预测实际效果，见表4，并绘制实际值和预测值序列图，见图5。实际值与本模型预测的结果基本一致，且未超出95%可信区间。其中，2019 年5、9、10 月预测值大于实际值，2018 年12 月～2019 年2 月和2019 年7、8月预测值小于实际值。

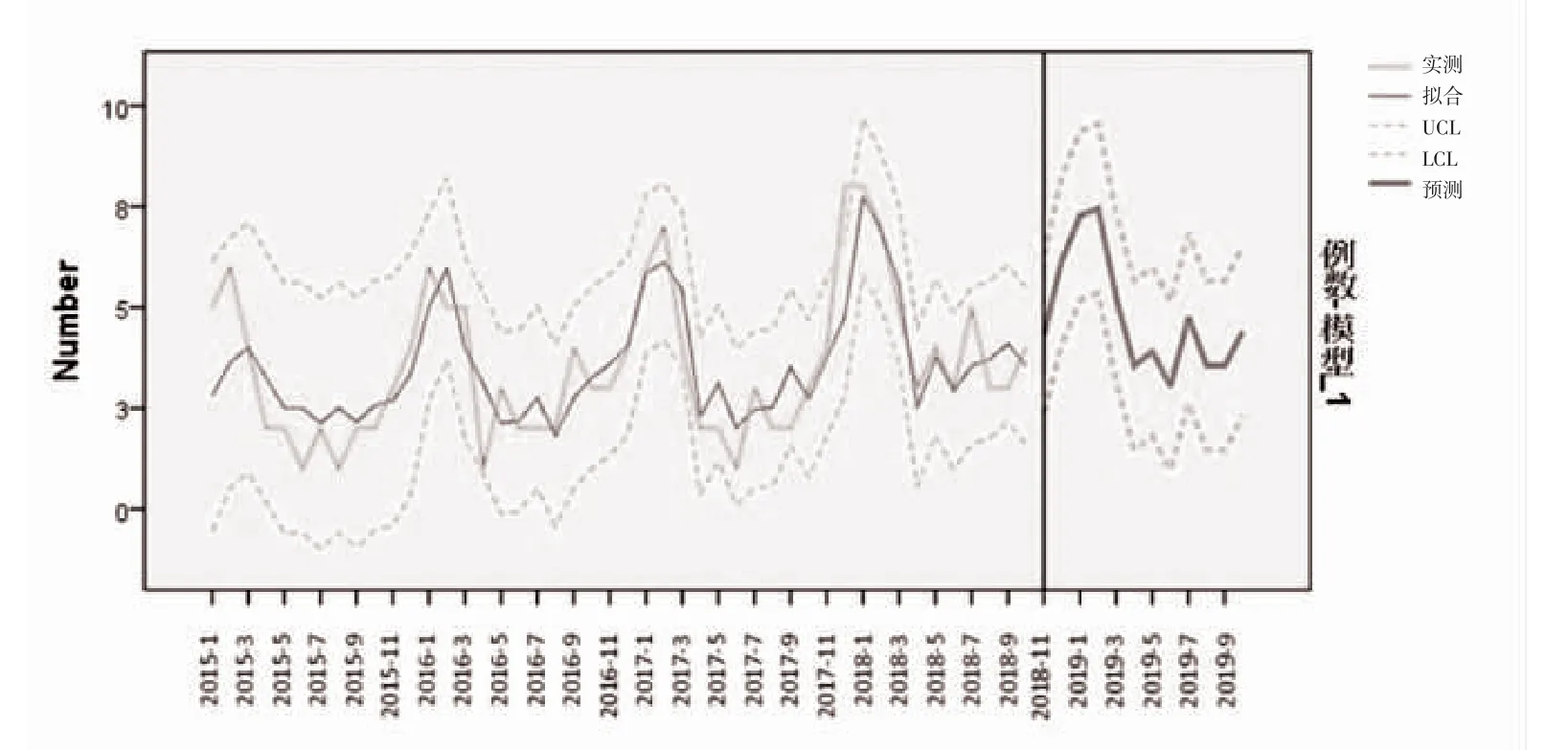
图5 AACG 就诊人数趋势预测分析图

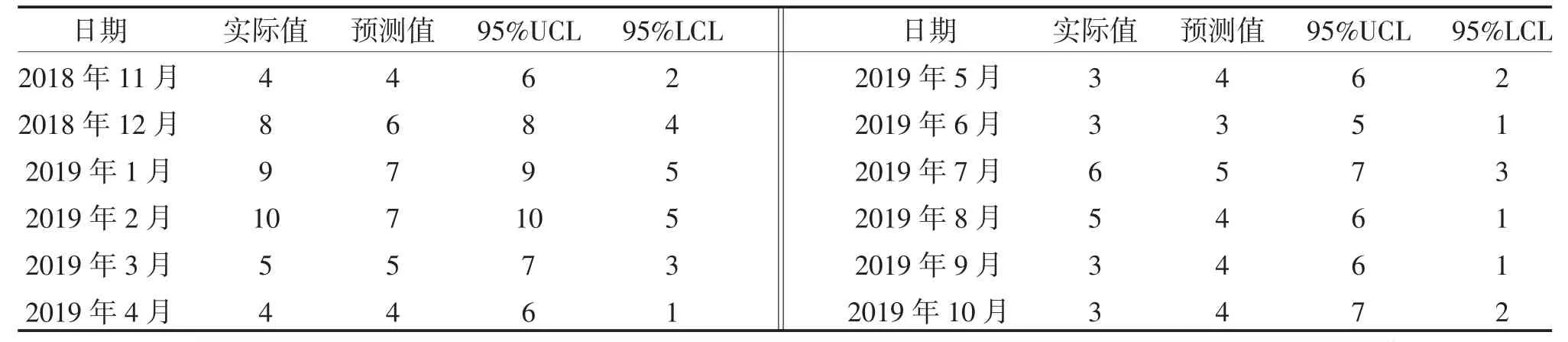
表4 AACG 就诊人数预测值与实际值比较（n）

3 讨论

3.1 AACG 发病的特征 AACG 是由于房角突然关闭，使得房水流出受阻，并最终导致眼压升高，其发生往往有内在的或外在的促发因素，临床上最多见的是情绪波动，亦见于过度疲劳、近距离用眼过度、暗室环境、全身疾病等等。本研究共收集因AACG就诊的患者226 例，其中50～70 岁最多，与临床流行病学研究结果一致[10]。

3.2 AACG 发病的季节规律 南昌处在北半球亚热带，气候属于亚热带季风气候，每年的7～8 月份温度最高，1～2 月份温度最低且温差变化较大。本研究对226 例AACG 患者不同月份就诊人数进行分析，就诊人次数与月份分布表表明，AACG 的多发于冬季（12 月～次年2 月）。从2015 年1 月～2019 年10月的AACG 就诊人数时间序列分析图可得出，AACG 就诊人数随时间波动，波峰为每年12 月～次年2 月。圆分布方法分析结果表明，每年的12 月12日是AACG 就诊高峰日。

3.3 气象因素与AACG 发病的关联 分析8 个气象因素与AACG 日就诊人数的关联，数据显示AACG与Ta、Th、T1 呈负相关（R=-0.216、-0.167、-0.171，P＜0.05），与Pa、Ph、Pl、Ha、Hl 呈正相关（R=0.048、0.049、0.041、0.079、0.074）。从相关系数值来看，AACG 发病与单一气象因素的相关系数较小。进一步多元逐步回归分析显示，Ta、Th、T1、Hl 与AACG就诊人次数有关（P＜0.05）。表明温度、气湿会影响AACG 的发病。分析其原因可能是温度突变影响了调节中枢，自主神经引起房角关闭，进而导致眼压的升高，并最终引起急性闭角型青光眼大发作。因此，需高度关注温度变化，温度骤降时，应当尽量避免户外活动；出门时，必须做好防寒保暖工作，避免闭角型青光眼大发作。

3.4 AACG 就诊人次数的预测模型 本研究构建了ARIMA 预测模型，该模型相比于线性回归模型，对波动性、随机性较大的数据拟合效果较好、预测精度较高，其将多种因素（包含未知因素）的综合效应都蕴含于时间变量，常用于预测某一疾病与季节变换的关系[11，12]。本研究以46 个时间点长度的AACG 就诊人数为预测数据，以12 个时间点的数据为验证数据，经过模型的识别、估计和诊断，最终明确含有气象因素的预测模型：ARIMA（1，0，0）（2，0，0）12模型，该结果表明平均温度等气象因子对AACG 就诊人数有一定影响。模型各参数、Box-Ljung 统计量、平稳R2、标准化BIC 和均方根误差等指标均表明ARIMA 模型对AACG 就诊人次数序列的拟合效果良好，进一步分析模型对AACG 发病的预测结果显示2018 年11 月1 日～2019 年10 月31 日模型预测值与具体情况基本一致，2018 年11 月1 日～2019年10 月31 日就诊人数各实测值均落入预测值的可信区间内，表明模型对AACG 就诊的预测分析实际效果较好，可用于预测分析AACG 就诊情况，能为AACG 的预防和治疗提供依据。

总之，AACG 多发于冬季，其发病与温度、气湿相关，气象因子之间协同作用影响AACG 的发生。温度骤变引起AACG 发生的风险升高。ARIMA（1，0，0）（2，0，0）12对AACG 的发病预测实际效果比较理想，可用于预测AACG 月就诊情况，实现警示预报功效。