胶囊机器人管内流场的数值模拟和实验测量

梁 亮,唐蒲华,刘 煜

长沙学院 机电工程学院,长沙 410022

0 引 言

无创诊疗技术是人类医学发展的方向,随着消化道遥控胶囊内镜的成功研制,胶囊机器人已成为人类医疗领域胃肠道应用的热点[1]。目前,研究的胶囊机器人按结构可分为光滑胶囊机器人[2]、螺旋胶囊机器人[3-4]和腿式胶囊机器人[5]等。其中,光滑结构是实际临床应用中的一种常用结构。由于采用电池、电线存在诸多问题,而磁场具有各种优势,因此胶囊机器人的驱动方式主要采用外磁场驱动。永磁体法是指利用外部永磁体的运动来驱动内部含磁铁的胶囊机器人作相应运动[6-7]。永磁体法控制原理简单、操作方便、易于商业化,其难点在于控制外部永磁体以实现对胶囊机器人作用力的平衡。

胶囊机器人对肠道的损伤主要来源于与肠道之间的接触摩擦和运行时黏液对肠道的压力。Zhang等[8]测量了胶囊机器人在离体猪肠内运动时的摩擦阻力。Li等[9]在胶囊机器人光滑表面上设计了一种压力传感器,用于测量胶囊机器人移动时与管道内壁的接触压力,并实现了数据的无线接收。胶囊机器人在肠道中运行时所受到的流体压力和阻力等参数的测量比较困难,目前还未见报道。

计算流体动力学(CFD)是一种流体流场的数值计算方法,广泛应用于计算流体机械的速度和力[10-11]。粒子图像测速(Particle Image Velocimetry,PIV)技术是一种瞬态、多点、无接触式的流体测速方法。PIV技术除向流场散布示踪粒子外,所有测量装置并不介入流场。PIV技术广泛应用于运动流体的速度场测量[12-13]。

本文将CFD方法和PIV技术应用于永磁体驱动的胶囊机器人中,研究胶囊机器人以不同转速在充满黏液的管道内旋进时,周围流体流场以及胶囊机器人所受到的黏液阻力、阻力矩和周围流体湍流强度等性能参数的变化情况,揭示运行参数对胶囊机器人运行性能影响的规律,为磁控胶囊机器人运行时的流场优化和最优运行方式设计奠定基础。

1 胶囊机器人结构和驱动原理

根据永磁体法,设计了一种磁控胶囊机器人,能在充满黏液的管道内做旋进(旋转和平移)运行。如图1所示,体外驱动永磁体形状为空心圆环,径向充磁,上半圆环是S极,下半圆环是N极。胶囊机器人内置一个实心圆柱磁铁,径向充磁,磁铁上半圆柱是S极,下半圆柱是N极。由于胶囊内窥镜在检查人体肠道过程中,时常与肠道壁接触,可通过控制外部永磁体和胶囊机器人之间的距离,使胶囊机器人贴近管道上壁并处于平衡状态。

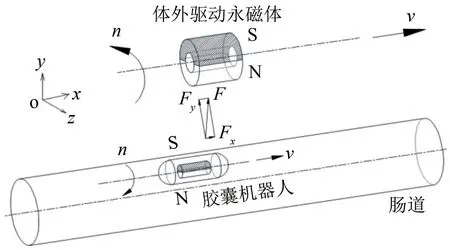
图1 胶囊机器人结构和驱动原理示意图Fig.1 Schematic diagram of structure and driving principle of capsule robot

开始时,外部永磁体位于胶囊机器人正上方(即y轴上方),胶囊机器人在磁力、重力、黏液浮力和管壁接触力作用下,达到平衡。启动外部永磁体绕自身中心轴(q轴,即x轴)旋转,内置磁铁的胶囊机器人也相应地随之绕自身x轴旋转,两者转速相同,方向相反。当外部永磁体沿着x轴正向直线运动时,外部永磁体对胶囊机器人的吸力F可分解为两个分量,一个分量沿着x轴正方向,驱动胶囊机器人沿着x轴做跟随等速直线运动,一个分量沿着y轴正方向,迫使胶囊机器人贴近管道上壁。胶囊机器人与管道上壁之间的接触力大小可以通过外部永磁体与胶囊机器人之间的距离来调节。

2 管道内流体的动力学控制方程

当胶囊机器人在充满流体的管道内运行时,管道内流体将会对胶囊机器人产生作用力,其大小可以通过计算与胶囊机器人邻近的管内流体流场来获得。假设管道内流体不受温度影响、不可压缩、满足质量守恒方程和动量守恒方程。

式 中:ρ为流体密度;(i、j、k分别为x、y、z轴的单位矢量);ux、uy、uz为流体速度矢量u在x、y、z方向的分量;p为流体 压力;τxx、τxy、τxz、τyx、τyy、τyz、τzx、τzy、τzz为因分子黏性作用而产生的黏性应力τ的分量;Fx、Fy、Fz为体积力,若体积力只有重力,且沿y轴竖直向下,则Fx＝0,Fy＝－ρg,Fz＝0。

式(1)和(2)为黏性流体动力学的控制方程[14],是流体流场数值计算的数学模型。要得到上述偏微分方程的解析解比较困难,可采用CFD数值计算方法,求解满足实际要求的近似解。求解的步骤大致为:运用Pro/E软件建立胶囊机器人系统的三维模型;运用Gambit软件划分网格并设置边界条件;运用ANSYS-Fluent软件求解参数并分析结果。

3 数值计算方法

3.1 胶囊机器人系统三维建模

运用Pro/E设计软件建立胶囊机器人系统的三维模型。机器人系统包括胶囊机器人、圆管和流体。胶囊机器人外径为10 mm,长度为18 mm,两端均为半球状帽,中间段为光滑圆柱。根据人体小肠直径范围,工作管道设计为管径18 mm,长度300 mm。管内充满密度800 kg/m3,动力黏度0．1 Pa·s的硅油流体,其性质接近于胶囊内镜检查时的肠道液。因为当消化道胶囊内镜实际应用到人体时,为了缩短胶囊内镜通过消化道的时间,提高胶囊内镜检查图像的清晰度,需要在检查人体小肠前,服用二甲硅油散和纯净水,类似于二甲硅油,这样能够有效去除小肠肠道内的气泡,起到理想的肠道清洁效果[15]。

为了模拟胶囊机器人周围流体的旋转,在胶囊机器人表面设计了一层包裹的流体(用于网格加密)。包裹流体的形状和胶囊机器人外形相同,厚度为0．5 mm,与圆管上壁面距离也为0．5 mm。即胶囊机器人外壳与管道上壁之间间隙为1．0 mm,它们相互靠近,但并不接触,以满足数值计算的需要。

3.2 胶囊机器人系统网格划分

对于充满在管道内的流体,设置两个流体区域,即机器人表面包裹的胶囊状流体区域和剩余流体区域。考虑到两个流体区域的几何形状,网格选择非结构化四面体网格,并对机器人表面包裹的胶囊状流体区域进行网格加密。胶囊状流体区域网格的间隔尺寸设置为0．5,剩余流体区域网格的间隔尺寸设置为1．3。

经过验证计算,在网格质量满足计算要求前提下,网格数达到20万时,满足网格无关性;当时间步长为0．0005 s时,满足时间独立性。最终,确定机器人表面包裹的胶囊状流体区域和剩余流体区域的网格数分别为17 300和234 464,时间步长确定为0．0005 s。胶囊机器人系统网格划分如图2所示。

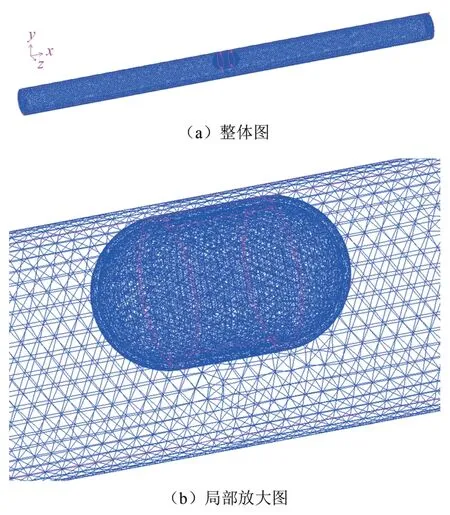
图2 胶囊机器人系统网格图Fig.2 Divided mesh of capsule robot system

3.3 模型选择和参数设置

当胶囊机器人在充满黏液的管道内旋进运行时,机器人周围流体除了沿管道轴向流动,还有切向运动,因此管道内流体状态为湍流,采用标准k-ε湍流模型,近壁处流动采用标准壁面函数处理。

根据实际情况,数值计算中机器人平移速度v固定为0．04 m/s,机器人转速n分为60、90、120、150和180 r/min。研究中,考虑流体重力,方向为y轴负方向;但不考虑机器人重力,因为实验时机器人处于平衡状态。对于流体流场压力和速度耦合方程的求解采用标准的SIMPLE算法,压力、动量、湍动能和耗散率的差分格式均为二阶迎风格式。为了模拟机器人表面邻近区域流体的运动,采用滑移网格方法进行处理,给定机器人表面邻近区域流体转速等于机器人转速。

根据肠道特点,管道两端设置为壁面,且不考虑流体的流动。初始条件设置为全部区域初始值为零。整个数值计算采用非稳态计算,并且使用动网格技术,假定机器人沿着x轴正方向在管道内作旋转直线运动。解算收敛精度满足:连续性,x、y、z方向速度,k,ε均为0．001。

4 实验测量方法

PIV测量方法是最直接的流体速度测量方法。从t1到t2的时间间隔(Δt)内,激光照射面上某一示踪粒子在该平面上运动的速度可以表示为:

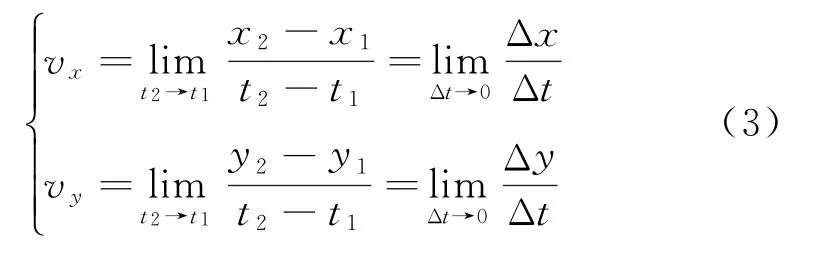
式中,v为速度,t为时间,x、y为位移。

当时间间隔Δt无限小时,式(3)为该示踪粒子在t1时刻的速度,即为t1时刻示踪粒子所在点的流体速度,再通过计算机逐点处理可获得t1时刻测试平面流体的速度场。

如图3所示,当胶囊机器人运行时,管内流场PIV测量原理为:通过计算机控制CCD(Charge Coupled Device)相机和同步器,同步器控制激光发生器产生脉冲激光,经导光臂引导至片光源镜头,片光源镜头垂直向上,通过水槽和水照射至玻璃管内待测区域(胶囊机器人运行区域的xoy截面),其中片光源厚度小于1 mm。CCD相机镜头和片光源镜头相互垂直,CCD相机与脉冲激光同步曝光拍摄示踪粒子图像,短时间拍摄多张图像,从而得出粒子(即流体)在流场中各点的速度矢量。

图3中,将胶囊机器人运行的玻璃圆管放入方形水槽的原因是:当片光源发射的片状激光直接照射在胶囊机器人运行的玻璃管表面时,由于空气和玻璃的密度相差较大,玻璃管表面又是圆弧形的,片状激光将会产生折射现象,不能在玻璃管内形成相同的片状照射面,并且示踪粒子的亮度也将降低,影响成像效果,导致PIV测量误差较大。为了避免或减少上述现象,将玻璃圆管放入方形玻璃水槽中,水槽内注入一定量的水,并完全淹没玻璃管。这时,片状激光首先垂直照射在方形玻璃水槽底部,不会发生折射,继续射入水槽后,由于水槽内水和圆管玻璃的密度相差不大,激光射入玻璃圆管内基本不会产生折射,从而在管道内部形成所需的片状激光区域,即胶囊机器人运行区域(xoy截面)。CCD相机光轴与片光源平面保持垂直是为了降低示踪粒子在CCD相机中的成像位移偏差。

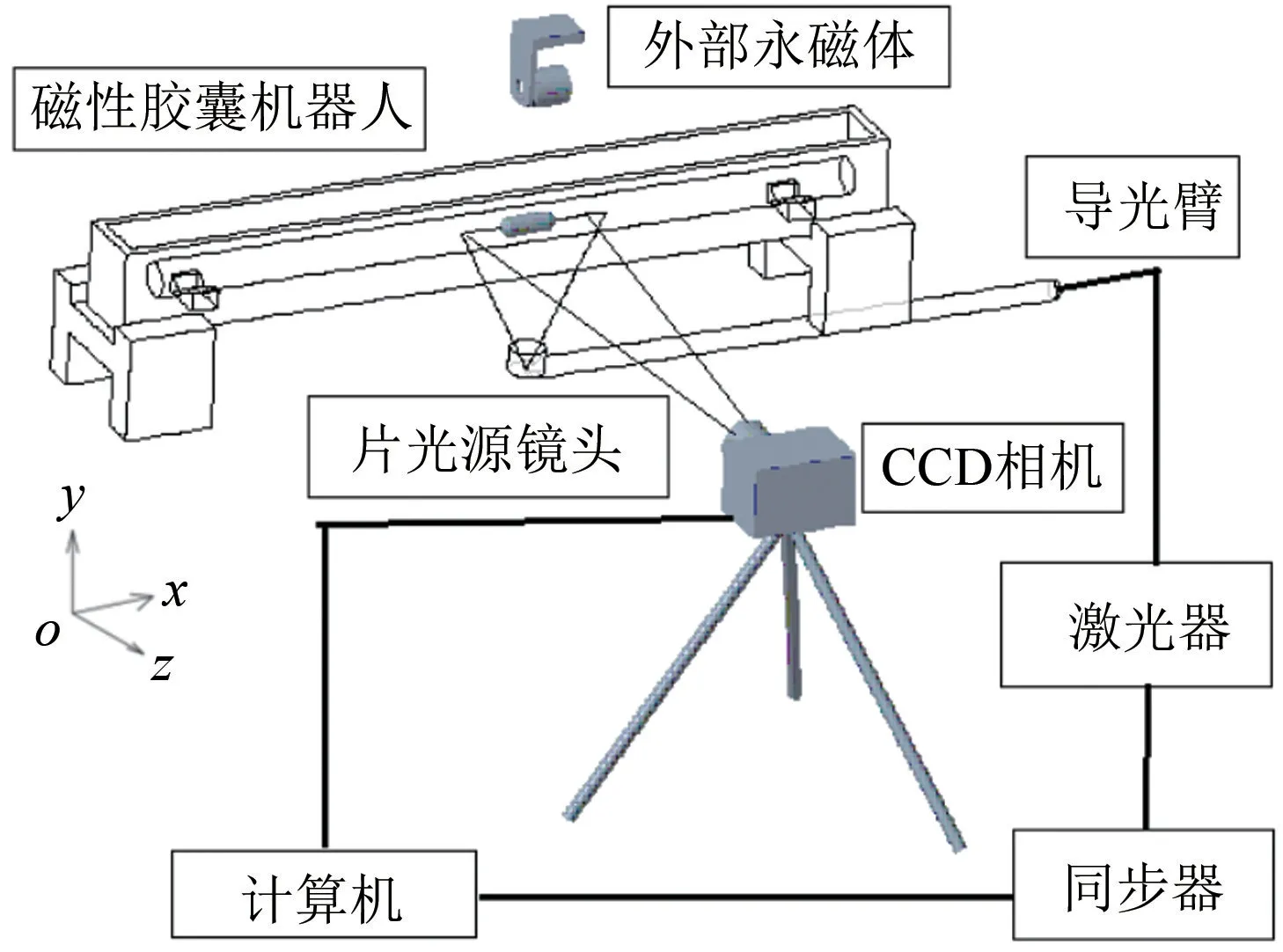
图3 管内流场PIV测量原理示意图Fig.3 Schematic diagram of PIV measurement principle of fluid flow field in pipe

本文设计制造了胶囊机器人,并搭建了管内流场PIV测量系统,如图4所示。该系统包括胶囊机器人磁驱动模块和PIV测量模块。胶囊机器人磁驱动模块主要包括三轴运动平台、旋转电机、控制器、数据采集卡、外部永磁体、磁性胶囊机器人(外径10 mm,长度18 mm)、试验管道(内径18 mm,长度300 mm)、上位机、工作台等。外部永磁体通过三轴运动平台和旋转电机,可以实现x,y,z等3个方向的平动以及绕y轴和自身中心轴(q轴,即x轴)的转动。PIV测量模块主要包括PIV系统、工作台架、玻璃水槽、水槽支架、垫片、压块等。PIV系统采用德国La Vision公司的粒子图像测速系统,主要包括:示踪粒子、光学照明系统、图像采集和处理系统。示踪粒子为Lavision公司提供的空心玻璃微珠,粒径8～12μm。激光器单脉冲能量为100 mJ,CCD相机分辨率为2048 pixel×2048 pixel,像素物理大小为7．4μm×7．4μm,两帧图像间隔时间设置为5 ms,经Da Vis软件处理后可显示管道内流体流场。

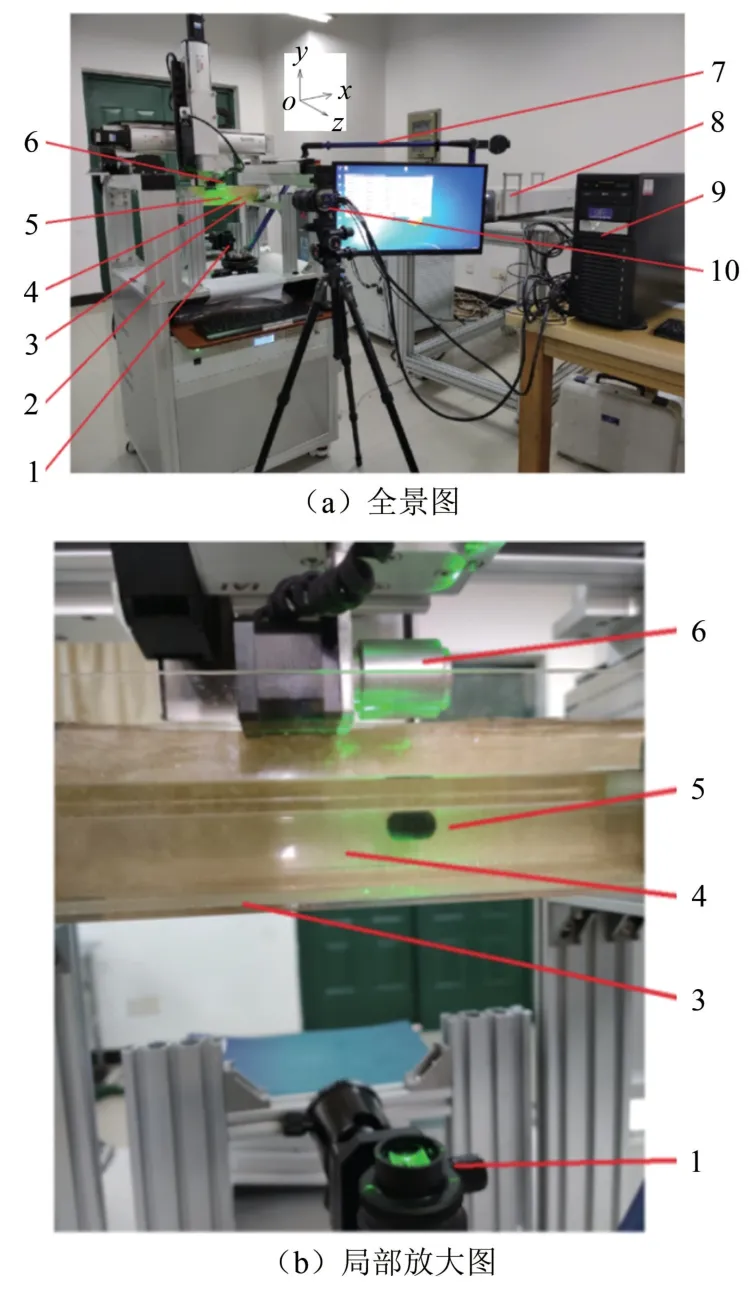
图4 胶囊机器人管内流场PIV测量实验系统Fig.4 PIV experimental system for measuring fluid flow field in pipe with capsule robot

图5是胶囊机器人样机,胶囊机器人采用3D打印而成,材料为生物塑料,表面选用黑色。

图5 胶囊机器人样机Fig.5 Capsule robot prototype

实验测量时,设置外部永磁体平移速度v为0.04 m/s,转速n＝150 r/min,胶囊机器人跟随外部永磁体在充满无色201甲基硅油的管道内做同速度的旋进运动。

5 结果与分析

涡量是流速的旋度,为流体旋转角速度的2倍,反映流场中各处流体微团绕其中心旋转的快慢。涡量是矢量,其方向由右手法则判定:右手握拳,四指为流体旋转方向,大拇指指向涡量方向[16]。

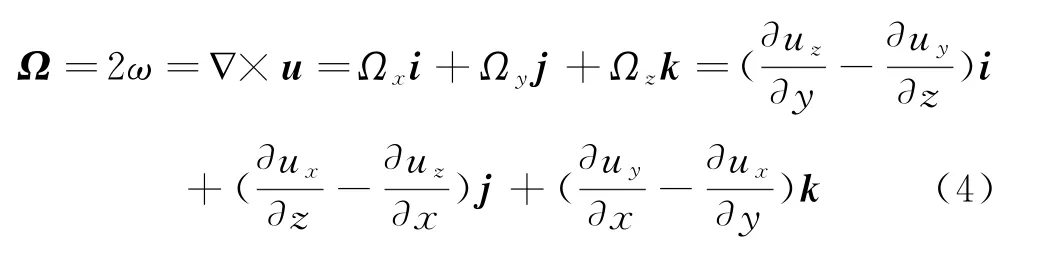
式中,Ω为涡量;u为流体线速度;ω为旋转角速度;i,j,k分别为笛卡尔直角坐标系中x,y,z轴的单位矢量;Ωx,Ωy,Ωz分别为Ω在x,y,z轴方向上的分量;ux,uy,uz分别为u在x,y,z轴方向上的分量。

如图6所示,以胶囊机器人中心竖直向下对应的管道底部位置为坐标原点,建立用于结果分析的二维直角坐标系,x轴正方向为水平向右,y正方向为竖直向上。

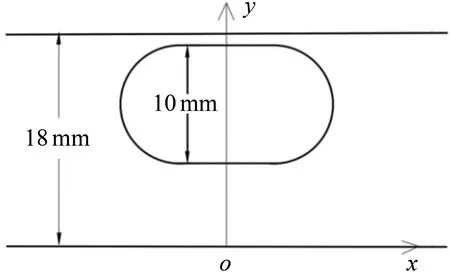
图6 管道内流体参考坐标系Fig.6 Reference coordinate system of fluid in the pipe

5.1 数值计算与实验测量比较

由于片光源放置在胶囊机器人中心正下方,片状激光沿着穿过胶囊机器人中心的xoy截面,从下往上照射,因此胶囊机器人与管道上壁面之间区域成为背光区域,实验测得此区域流场实际是片激光照射到胶囊机器人底面产生的折射光照射到管内胶囊机器人前方流体时所拍摄出的流场。而在数值计算中,依据标准壁面函数,当胶囊机器人以平移速度v＝0．04 m/s,转速n＝150 r/min旋进运行时,计算得到此区域流体在x方向速度如图7所示。从管道上壁面到机器人表面的流体速度规律为:从0 m/s增加到机器人x方向平移速度0．04 m/s。

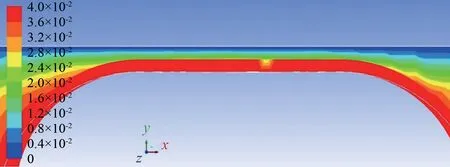
图7 胶囊机器人与管道上壁面区域流体x方向速度(n＝150 r/min)Fig.7 x-directional velocity of fluid between capsule robot and upper wall of pipe(n＝150 r/min)

图8和图9分别是胶囊机器人以平移速度v＝0.04 m/s,转速n＝150 r/min旋进运行时,管内穿过胶囊机器人中心的xoy截面流体速度流线叠加和涡量图。可以看出,数值计算的胶囊机器人周围流体流线的形状和分布以及流体速度大小都与实验测量结果基本相同,并且在胶囊机器人底部形成了一个较大尺寸的流体旋涡。数值计算的胶囊机器人周围流体涡量分布规律和大小也与实验测量结果基本相似。

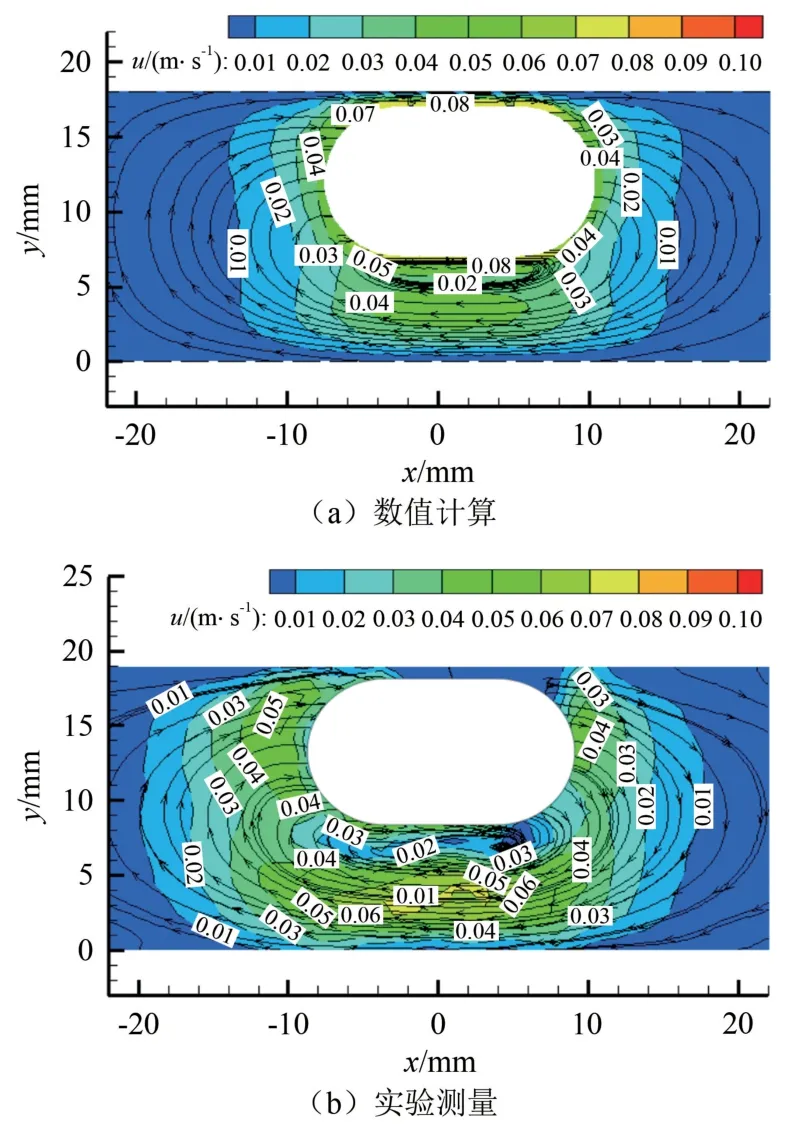
图8 胶囊机器人周围流体的流线和速度云图叠加Fig.8 Superimposition of the streamlines and velocity clouds of the fluid around capsule robot

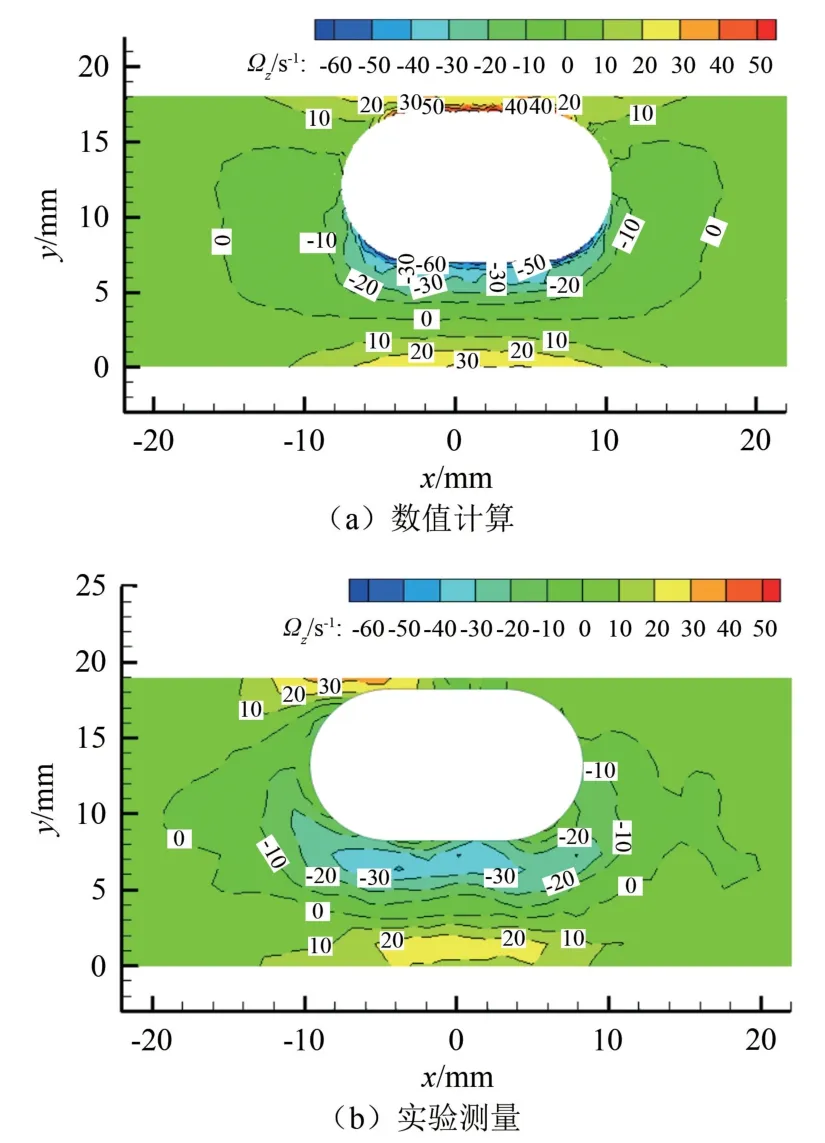
图9 胶囊机器人周围流体的涡量Fig.9 Vorticity of the fluid around capsule robot

图10是以图6所示坐标系中胶囊机器人下方区域流体绕z轴涡量的CFD数值计算和PIV实验测量结果的对比图。从图中可以看出,从管道底部往胶囊机器人底部方向,流体绕z轴涡量是从正值到负值,逐渐递减。CFD数值计算结果与PIV实验测量结果的变化趋势和数值大小基本吻合,进一步证明本文所采用的CFD方法是合理和正确的。

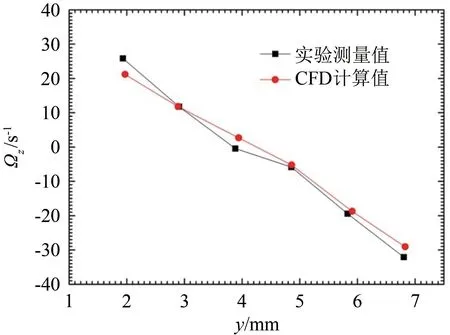
图10 胶囊机器人下部区域流体绕z轴涡量数值计算和实验测量的对比(v＝0.04 m/s,n＝150 r/min)Fig.10 Comparison of numerical calculation and experimental measurement of fluid vorticity around z-axis at the lower zone of capsule robot(v＝0.04 m/s,n＝150 r/min)

5.2 转速影响研究

图11是胶囊机器人平移速度v＝0．04 m/s,转速n＝60～180 r/min时,管内穿过胶囊机器人中心的xoy截面流体的速度云图和流线叠加。

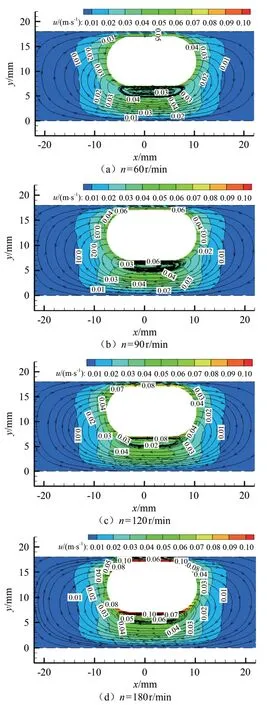
图11 数值计算的不同机器人转速下管内流体速度云图和流线叠加Fig.11 Fluid velocity nephogram and streamline superposition in the pipe at different rotational speeds of robot by numerical calculation

结合图8(a)可以看出,当胶囊机器人贴近管道沿着x轴方向向右旋进运行时,胶囊机器人周围流体向尾部作环流运动,同时在胶囊机器人底部会形成较大尺寸的旋涡。胶囊机器人头部和尾部区域流体的速度大小基本等于旋进胶囊机器人的平移速度大小。随着胶囊机器人转速的增大,胶囊机器人周围流体的流动和分布规律基本相似,胶囊机器人四周和下部区域流体速度会略微增大,流体流线略微混乱。从流体速度和流线的叠加图中能够看到一定的流体涡结构,但较小尺寸的旋涡分布较为混乱,难以辨别和量化,因此进一步采用涡量图进行分析。

图12和13分别是胶囊机器人平移速度v＝0．04 m/s,转速n＝60～180 r/min时,穿过胶囊机器人中心的xoy截面流体的涡量分布图和涡量最大负值。图中红色和黄色区域,涡量为正值,表示流体绕z轴逆时针旋转。蓝色和蓝绿色区域,涡量为负值,表示流体绕z轴顺时针旋转。颜色越深,表示涡量强度越大。

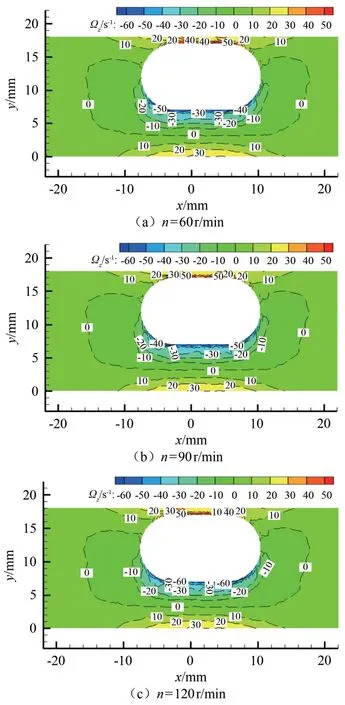
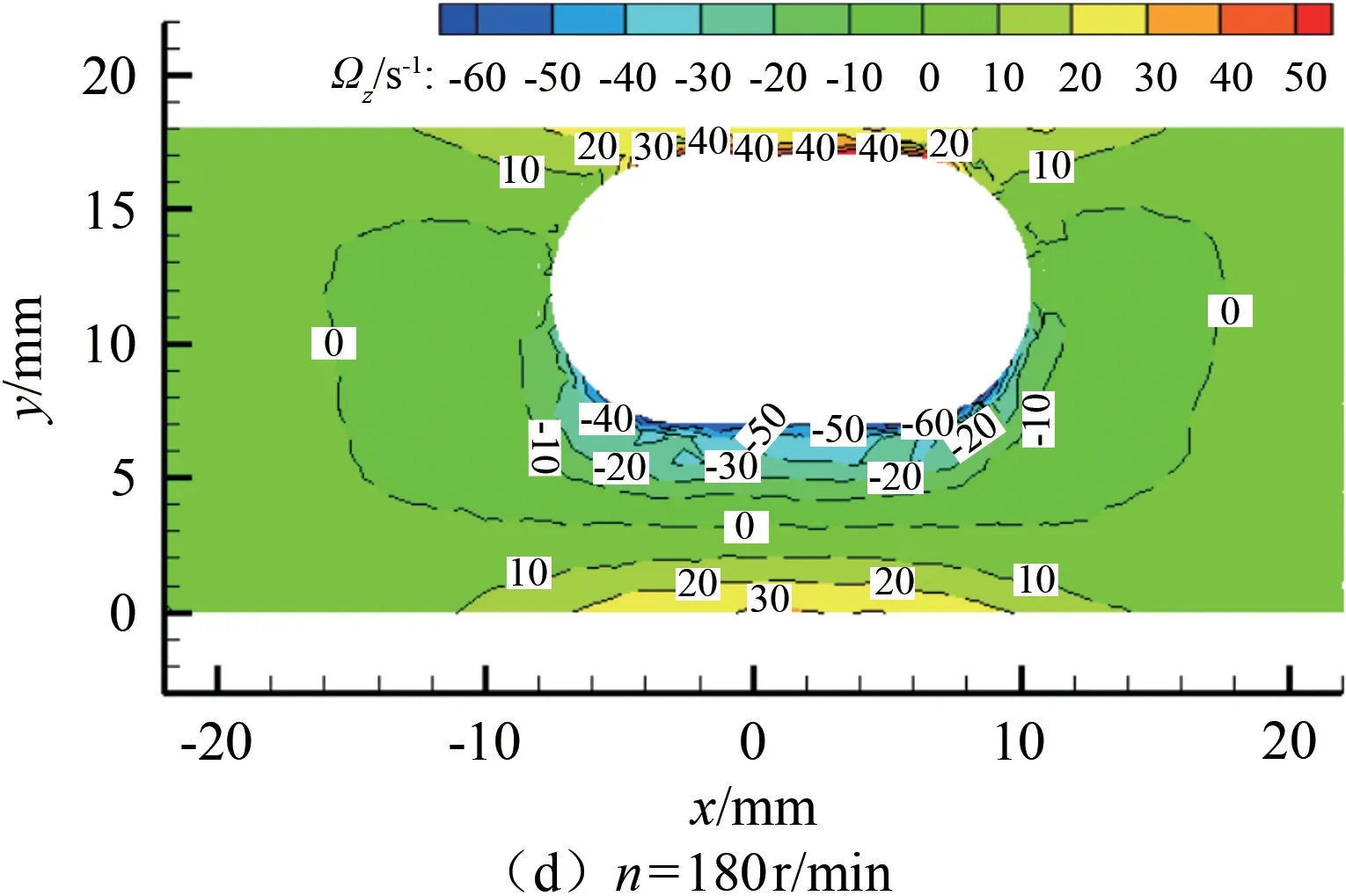
图12 数值计算的不同机器人转速下管内流体涡量Fig.12 Fluid vorticity in the pipe at different rotational speeds of robot by numerical calculation

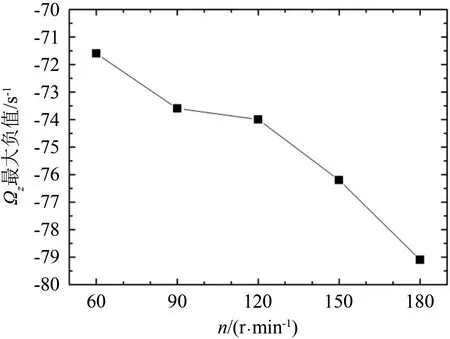
图13 数值计算的不同转速下机器人下方流体绕z轴涡量最大负值Fig.13 Maximum negative vorticity of fluid under the robot around z-axis at different rotational speeds of robot by numerical calculation

结合图9(a)可以看出,胶囊机器人底部大部分邻近区域流体涡量为负值,而靠近管道底部区域流体涡量为正值。随着胶囊机器人转速的增大,胶囊机器人周围流体的涡量分布规律相似,涡量大小略微增大,说明流体旋转强度略微增大,流体混乱程度略微增加,胶囊机器人运行的平稳度略微降低。在胶囊机器人底部与管道底部之间的中段,存在一条涡量为零的带状区域,分别向胶囊机器人的头部和尾部延伸。湍流强度是描述流体湍流运动最重要的特征量,是衡量湍流强弱的相对指标。湍流强度越大,流体相对运动越紊乱,机器人运行时所受阻力相对越大,能耗越高。

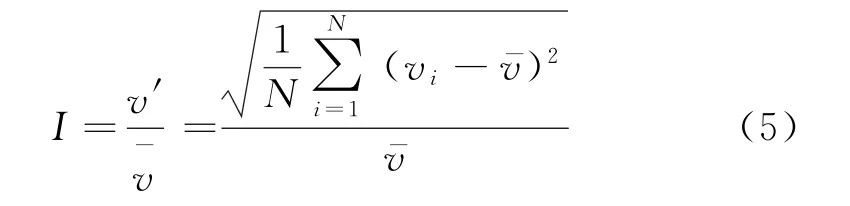
式中:I为胶囊机器人周围流体平均湍流强度;v′为脉动速度均方根;v－为平均速度;N为一段时间内采样点数。

胶囊机器人性能参数主要包括胶囊机器人所受阻力、阻力矩和周围流体平均湍流强度等。图14～16是胶囊机器人平移速度v＝0．04 m/s,转速n＝60～180 r/min时,胶囊机器人前进方向(x轴)所受阻力、阻力矩与其周围流体平均湍流强度的大小值。

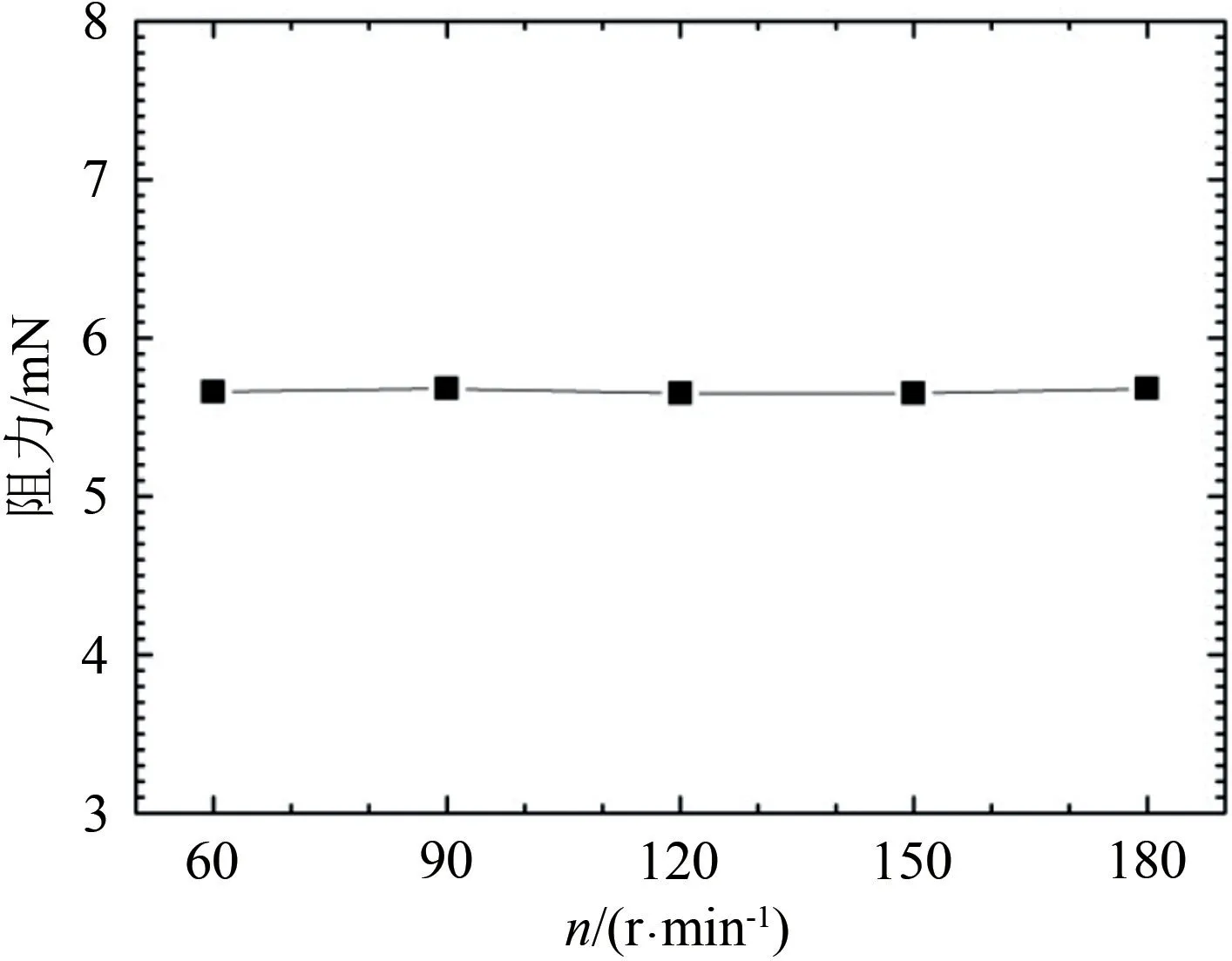
图14 机器人前进方向所受阻力与机器人转速关系Fig.14 Relationship between the resistance in the forward direction of robot and the rotational speed n

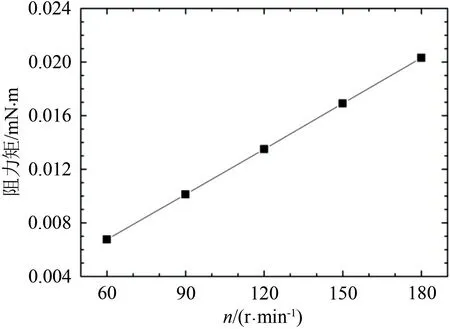
图15 机器人前进方向所受阻力矩与机器人转速关系图Fig.15 Relationship between the resisting moment in the forward direction of robot and the rotational speed n

图16 机器人周围流体平均湍流强度与机器人转速关系Fig.16 Relationship between the average turbulent intensity of fluid around robot and the rotational speed n

随着胶囊机器人转速的增大,胶囊机器人前进方向所受阻力矩和其周围流体平均湍流强度均增大,而胶囊机器人前进方向所受阻力基本不变。这说明,胶囊机器人转速的增加会增大机器人工作的阻力矩,增强机器人周围流体脉动强度,导致机器人运行的平稳性降低,能耗增加,但并不会增大机器人运行时所受阻力。进一步计算表明,胶囊机器人运行所受阻力与平移速度成正比。

6 结 论

1)设计制造了一套永磁体法驱动的胶囊机器人,并搭建了管内流场实验测量系统。采用CFD方法分析了随着胶囊机器人转速的变化,管内流场的流线、速度、涡量等流场信息以及胶囊机器人所受到的黏液阻力、阻力矩和周围流体湍流强度等性能参数的变化情况。

2)采用PIV实验系统测量的胶囊机器人周围流体流线的形状、分布、流体速度大小、涡量分布规律和大小都与数值计算结果吻合较好。定量研究表明,胶囊机器人下部区域流体z方向涡量的CFD数值计算结果与PIV实验测量结果的变化趋势完全相同,大小接近,证明本文所采用的CFD方法是合理和正确的。

3)数值计算表明,随着胶囊机器人转速的增大,胶囊机器人周围流体的流动和分布规律基本相似,胶囊机器人四周和下部区域流体速度会略微增大,流体流线略微混乱;并且胶囊机器人周围流体的涡量分布规律也相似,涡量大小也略微增大,说明流体旋转强度略微增大,流体混乱程度略微增加,胶囊机器人运行的平稳度略微降低。随着胶囊机器人转速的增大,胶囊机器人前进方向所受阻力矩和其周围流体平均湍流强度均增大,即机器人运行的平稳性降低,能耗增加;但胶囊机器人前进方向所受阻力基本不变,胶囊机器人运行时所受阻力与平移速度成正比。

4)本文所采用的CFD方法和PIV技术可以适用于较小尺寸的胶囊机器人在液体环境中的流场和力学计算与测量。