基于运动学模型的平行泊车轨迹规划研究
雷 超
(华南理工大学机械与汽车工程学院,广东 广州 510640)
自动泊车系统关键技术主要包括车辆定位、车位检测、轨迹规划和轨迹跟踪。本文主要针对自动平行泊车轨迹规划进行研究。文献[1]采用圆弧-直线组合的方法设计了狭小空间的泊车路径,该泊车路径存在曲率突变,跟踪过程中需要停车转向;文献[2]、[3]采用反正切函数设计泊车路径,解决了原地转向问题,但由于曲线变化不灵活,需要较大车位空间。文献[4]为解决平行泊车两段圆弧路径曲率不连续的问题,在圆弧路径两端使用回旋曲线进行过渡连接使得曲率连续变化;文献[5]、[6]和[7]分别使用贝塞尔曲线、五次多项式曲线和sigmoid曲线设计了曲率平滑的泊车路径,但这些曲线缺乏灵活性,为了满足避碰要求需要较大车位空间;文献[8]采用B样条曲线并考虑避碰约束、转向性能约束等设计了曲率连续的泊车路径,但是曲率变化不够平缓。
为此,本文提出了一种基于车辆运动学模型的泊车轨迹规划方法,通过该方法规划得到的泊车路径优点在于路径曲率连续且变化平顺。
1 车辆运动学模型的建立
建立一个合理有效的车辆模型是进行轨迹规划和轨迹跟踪控制的前提,文献[9]中使用的是一种经典的车辆运动学模型,其可以很好地模拟车辆低速行驶的运动状态,如式(1)所示:

(1)
式中:x,y为车辆后轴中点坐标;v为车辆后轴中点速度;φ为车辆航向角;δ为等效前轮转角;L为轴距。图1为车辆运动学模型示意图。将车辆简化为一个矩形,其中A、B、C、D分别为车辆轮廓的4个顶点,Lf,Lr和W分别为车辆前悬长、后悬长和车宽。

图1 车辆运动学模型
将式(1)以T为周期进行离散化可得如下离散化模型,即第(k+1)个离散点参数可以由第k个离散点参数表示:

(2)
式中:a为车速变化率。
本文建立的平行泊车车库模型如图2所示,以车库左下角顶点为坐标原点建立坐标系O-XY,其中WA,HP,WP分别为道路宽度、车位宽度、车位长度,虚线与实线之间的距离为本文设定的安全距离ε。

图2 平行泊车车库模型
2 平行泊车轨迹规划
泊车是一个从低约束区的车库外驶入高约束区的车库内的运动过程,而车辆泊入车位与驶出车位是一个可逆的过程,因此本文首先规划出一条从高约束区的车库内驶出至低约束区的车库外的泊车轨迹(逆泊车轨迹),再通过逆变换得到泊车轨迹。该方法相较于传统的由车库外至车库内的泊车轨迹规划方法,能带来极大的简化。
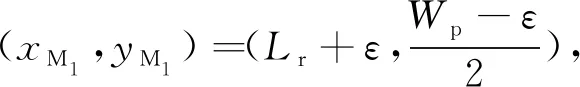

图3 平行泊车轨迹规划过程分析
对于车辆而言,当给定速度和转角输入后,车辆会相应产生位移,车辆在行驶状态(车速不为零)中进行转向驶过的路径是曲率连续的,而如果出现中途停车转向,那么前后路径的曲率将会发生突变。本文在进行轨迹规划时利用这一特点设计了曲率连续变化的轨迹。


图4 前轮等效转角

图5 后轴中点速度
(3)
在式(3)中,未知变量为最大等效前轮转角δ1、M2M3段对应的时间t1和M4M5段对应的时间t2。当这3个未知变量确定时,图4和图5所示的转角、速度与时间的变化关系就确定了。由式(2)、逆泊车轨迹起点M1坐标和转角与速度曲线可以递推得到逆泊车轨迹所有点位置,即可得到如图3中所示的M1→M2→…→M6的运动轨迹。
给定这3个未知参数一个取值范围,当δ1,t1和t2取不同值进行组合时,就可以得到不同的转角和速度曲线,如图4和图5所示,从而得到不同的泊车路径。当δ1,t1和t2取值范围合适时,可以遍历得到所有可行的泊车路径。考虑车辆本身的最大转向角度限制,本文将δ1的取值范围设定为0~0.6 rad。经过MATLAB仿真实验得出:当t1和t2的取值大于5 s时,得到的路径必会导致车辆与车库边界发生碰撞,因此将t1和t2的取值范围设定为0~5 s。以0.05 rad和0.5 s的间隔遍历转角δ1以及时间t1和t2的取值范围即可得到所有可行的泊车轨迹曲线簇,如图6所示,通过约束分析并建立代价函数即可求出一条最优轨迹。
车辆在运动过程中,为避免与障碍物发生碰撞,参考图4,需要满足的避碰和转向性能约束有:1)车辆左前顶点A(xA,yA)应避免与道路边界发生碰撞;2)车辆右前顶点B(xB,yB)应避免与泊车位右边界发生碰撞;3)车辆右后顶点C(xC,yC)应避免与泊车位底部边界相碰;4)前轮转角值应不超过车轮最大转角值。此外,车辆还受到几何约束,车辆任意一点坐标可由后轴中点坐标和车辆航向角通过几何关系表示。综合考虑避碰约束、转向性能约束和几何约束,以终点位置与车库边界的横向偏差、转角δ1(对应轨迹平缓程度)和泊车时间t的加权和的最小化为优化目标,建立式(4)所示优化目标函数J(δ1,t1,t2),通过求解该函数即可从图6所示的可行泊车轨迹曲线簇中得到一条最优的轨迹。

图6 泊车轨迹曲线簇
minJ(δ1,t1,t2)=
(4)
式中:k1和k2为加权系数;δmax为车辆最大等效前轮转角;yM6为泊车起始点后轴中点的纵坐标。
3 仿真分析


表1 轨迹规划仿真参数
在相同的仿真条件下将所设计的平行泊车路径与目前常见的双圆弧路径和三次B样条路径进行对比。图7为3种路径规划方法得到的平行泊车路径对比,图8为3种路径对应的曲率变化对比,从图中可以看出,双圆弧路径曲率发生了突变,需要在泊车过程中进行停车转向。三次B样条路径曲率连续但变化不平稳,波动较大,不利于跟踪控制。而本文所设计的平行泊车路径不仅曲率连续变化,并且变化平缓,曲率绝对值最大值为0.228 m-1。图9为本文规划的平行泊车轨迹对应的速度和等效前轮转角变化曲线,转角最大值为0.592 rad。图10为车辆按照本文所设计路径运动时车辆轮廓包络线,从图中可以看出所设计的路径是满足避碰约束条件的,可实现车辆平顺、安全的泊入车位。为验证本文规划方法对不同大小车辆的适用性,选用某C级车型作为对照组,车辆尺寸如下:轴距2.75 m,前后悬长分别为0.966 m和1.095 m,车宽1.86 m。仿真结果如图11和图12所示,对照组曲率绝对值最大值为0.217 m-1,等效前轮转角最大值为0.596 rad。从仿真结果来看,本文规划方法对不同大小车辆均适用。

图7 泊车路径

图8 泊车路径曲率

图9 车速和等效前轮转角

图10 车辆运动包络线

图11 泊车路径对比

图12 曲率、车速和转角对比
4 结束语
本文根据泊车经验设计了平行泊车转角和速度随时间的变化历程,通过遍历所设计的转角和速度曲线获取了所有可行的泊车轨迹曲线簇,并通过优化求解得到其中最优的泊车轨迹。从仿真结果来看,该方法综合了双圆弧路径和B样条路径的优化,既有B样条路径曲率连续的优点,又有双圆弧路径曲率简单无波动的优点。

