基于Chirp-Z变换的结构热模态试验方法
宋巧治,李晓东,杨文岐
(中国飞机强度研究所,陕西 西安 710065)
1 引 言
高超声速飞行器在飞行过程中受到严酷的气动加热,受温度分布不均引起的热应力以及高温引起的材料性能变化共同作用,结构的固有振动特性发生改变。同时,在整个飞行包线内,结构的动态特性随着时间变化,从而造成结构的振动响应及颤振特性的时变特性,对结构的动稳定性及动态响应特性产生明显影响。为此,需要对结构动参数的时变特性进行分析和测试。由于分析过程中做了大量简化,因此分析结果无法精确反映结构的动态特性以及其时变特性。当前,结构的动态特性仍需要依赖试验手段,而时变结构试验测试则依赖于时变参数识别算法。
时变结构实际上不存在模态概念,为了对照时不变结构,学者提出了伪模态参数的概念,即在一定时间内将结构看作时不变系统,将模态参数的概念应用于结构分析中。国内外对时变结构伪模态参数识别算法的研究较多,一类是基于传统频率方法的改进方法,为了突出时变特性,称为时频方法(Time-frequency analysis,TFA)[1],其相对成熟的方法主要包括Gabor展开[2](Gabor expansion)、短时傅里叶变换(Short Time Fourier Transform,STFT)、小波变换(Wavelet Transform,WT)以及Wigner-Ville分布[3]。另一类是基于Hilbert-Huang变换(HHT)的经验数据分析方法。
经典的傅里叶变换无法反映结构的时变特性,基于傅里叶变换改造的短时傅里叶变换方法虽然可以获得信号的时频特性,但是由于时间分辨率和频率分辨率相互矛盾,因此获得的时频数据无法精确体现参数的时变特性。为此,学者提出了调频Z变换(Chirp-Z)方法[4],该方法具有以下优点[5]:
(1)不必增加采样点数即可提高频率分辨率、频率、幅值及相位精度,非常适合瞬态和短样本信号的频率细化。
(2)不需要进行滤波等处理,可以避免由滤波等引入的误差。
(3)输入点数和输出点数可以不相等,且与频率分辨率相互独立,灵活性好,当选带在频谱上滑动时,只有部分参数需要重新计算。
(4)计算效率较高,Chirp-Z的基础运算依然是快速傅里叶变换(FFT),因此FFT加速算法在Chirp-Z方面依然有效,同时对于非2的指数长度数据处理,Chirp-Z效率要高于FFT算法。
国内外对Chirp-Z变换进行了大量研究,并在多个领域进行了实际应用,获得了良好的应用效果,尤其在频响函数和频谱细化等方面获得了大量应用[6-8]。但是,当前的研究主要集中在频谱细化等方面[9],在时变结构的参数识别方面研究较少。
本文基于Chirp-Z变换方法,对频响函数进行细化,解决短时傅里叶变换的时间分辨率与频率分辨率的矛盾,对时变结构的动态参数识别方法进行了研究,并通过算例对本文提出的方法进行了测试与验证,对热环境下结构的响应试验数据进行了分析,获得了频率的时变特性。
2 算法原理
线性Chirp-Z变换算法可以密集计算局部频谱,提高局部频谱分辨率。根据单频信号加窗理论,频谱幅值最大点出现在真实频点上。因此,在高分辨率下,找到频谱的极大值,即可认为其是真实频点。Chirp-Z变换算法分析如下:
设x(n)表示N点序列,0≤n≤N-1,其Z变换为:
(1)
式中:
zk=AW-kk=0,1,…,M-1
(2)
A=A0ejθ0
(3)
W=W0e-jφ0
(4)
其中,A0是第一个抽样点的矢量半径的长度,θ0为起始抽样点的相角,φ0为相邻抽样点的角度差。φ0取值不同时代表的方向不同,φ0>0时为逆时针,φ0<0时为顺时针。W0为螺线的伸展率,W0>1时螺线内缩,W0<1时螺线外伸,W0=1时则表示半径为A0的一段圆弧。如果A0=1,则表示单位圆上的一段圆弧。若有θ0=0,φ0=2π/N,M=N,即为序列的DFT[10]。Chirp-Z变换在单位圆上的螺旋采样点如图1所示。
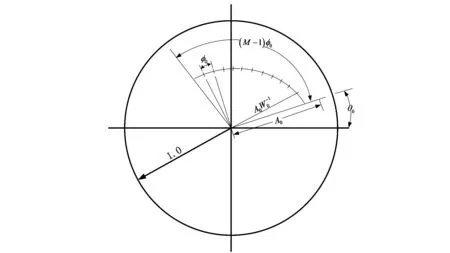
图1 Chirp-Z变换在单位圆上的螺旋采样点
将式(2)-式(4)代入式(1)中,可以得到:
(5)
由布鲁斯坦公式可以得到:
(6)
式(5)可以转化为:
(7)
令:
(8)
(9)
则有:
(10)
式(10)可以写作卷积形式:
(11)
Chirp-Z变换的运算流程如图2所示。
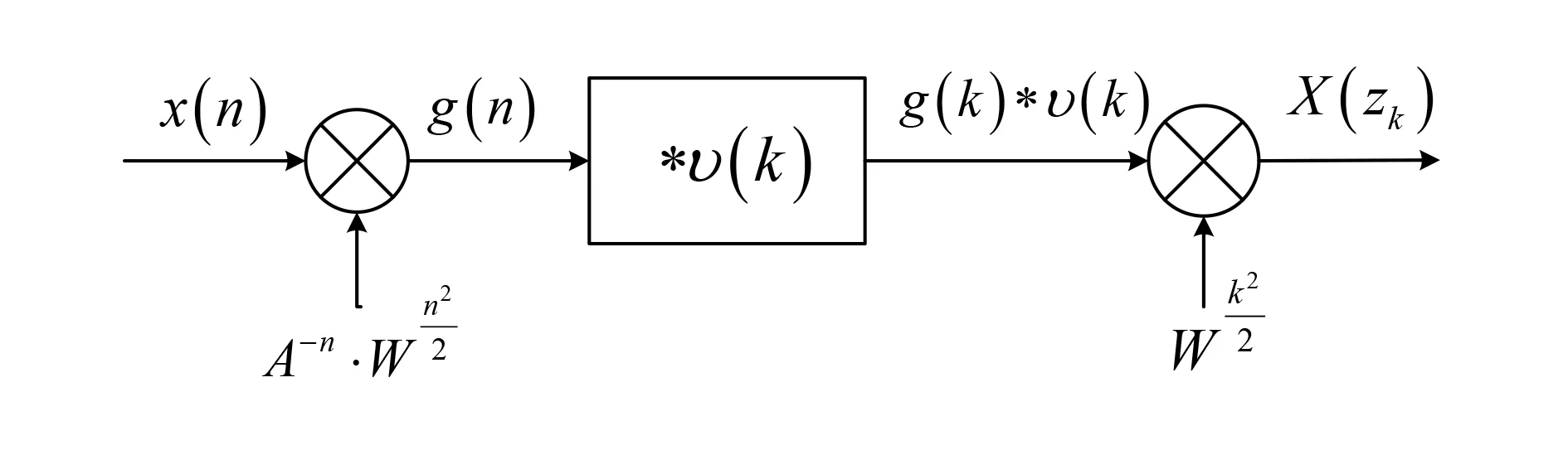
图2 Chirp-Z变换流程图
3 算例验证
为了验证算法的精度,本文采用一个三自由度系统进行分析(如图3所示)。三自由度系统的质量阵是随时间变化的,以此来模拟时变结构的时变特性。结构质量阵、刚度阵以及阻尼阵由式(12)描述,其中,ω为结构质量阵变化频率,本文中采用0.1257,对应质量阵变化频率0.02Hz。

图3 三自由度系统图示
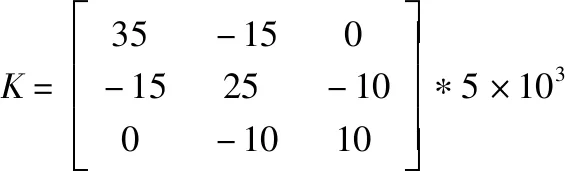

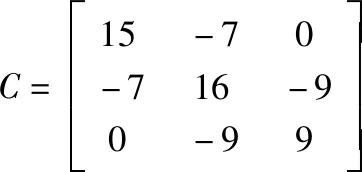
(12)
采用白噪声信号作为系统激励,对图3所示的质量块1进行激励,其余两个质量块激励为0,激励时域信号如图4所示。对系统的位移响应进行分析求解,获得了3个质量块的响应时间历程,如图5所示。

图4 在质量块1上施加的随机信号
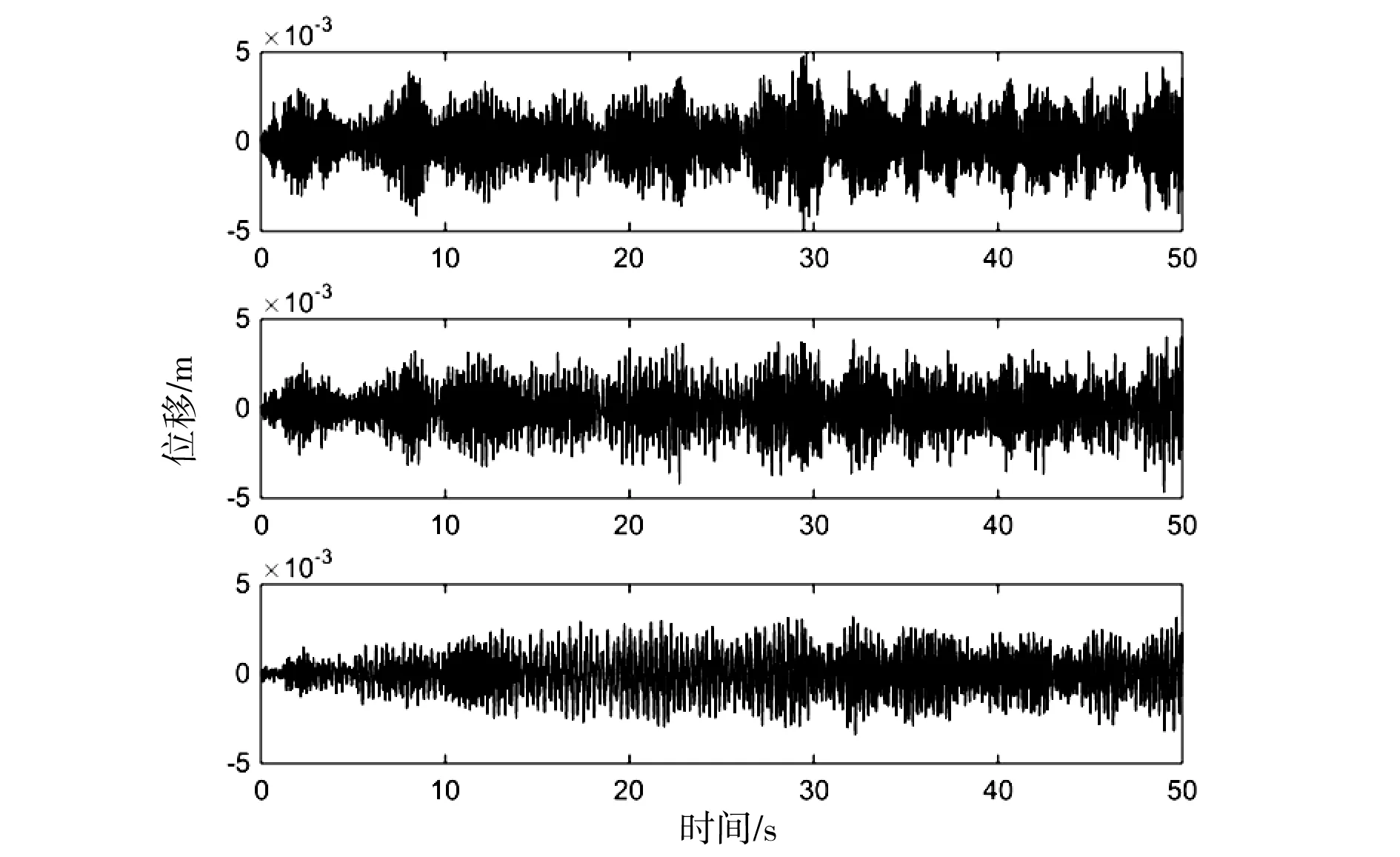
图5 3个质量块的位移响应信号
通过时间冻结法,将系统响应划分为若干区间,并认为在一定时间内,结构的频率变化不大。基于以上假设,对每个区间,利用Chirp-Z变换对响应信号进行处理,获得频率细化的响应频谱,通过分析可以获得结构的频率变化情况,并与理论结果进行了对比。图6给出了结构三阶频率的理论值以及Chirp-Z变换辨识值的对比,可以看出,两者吻合很好,证明了该方法在时变系统参数识别方面具有较高的识别精度。
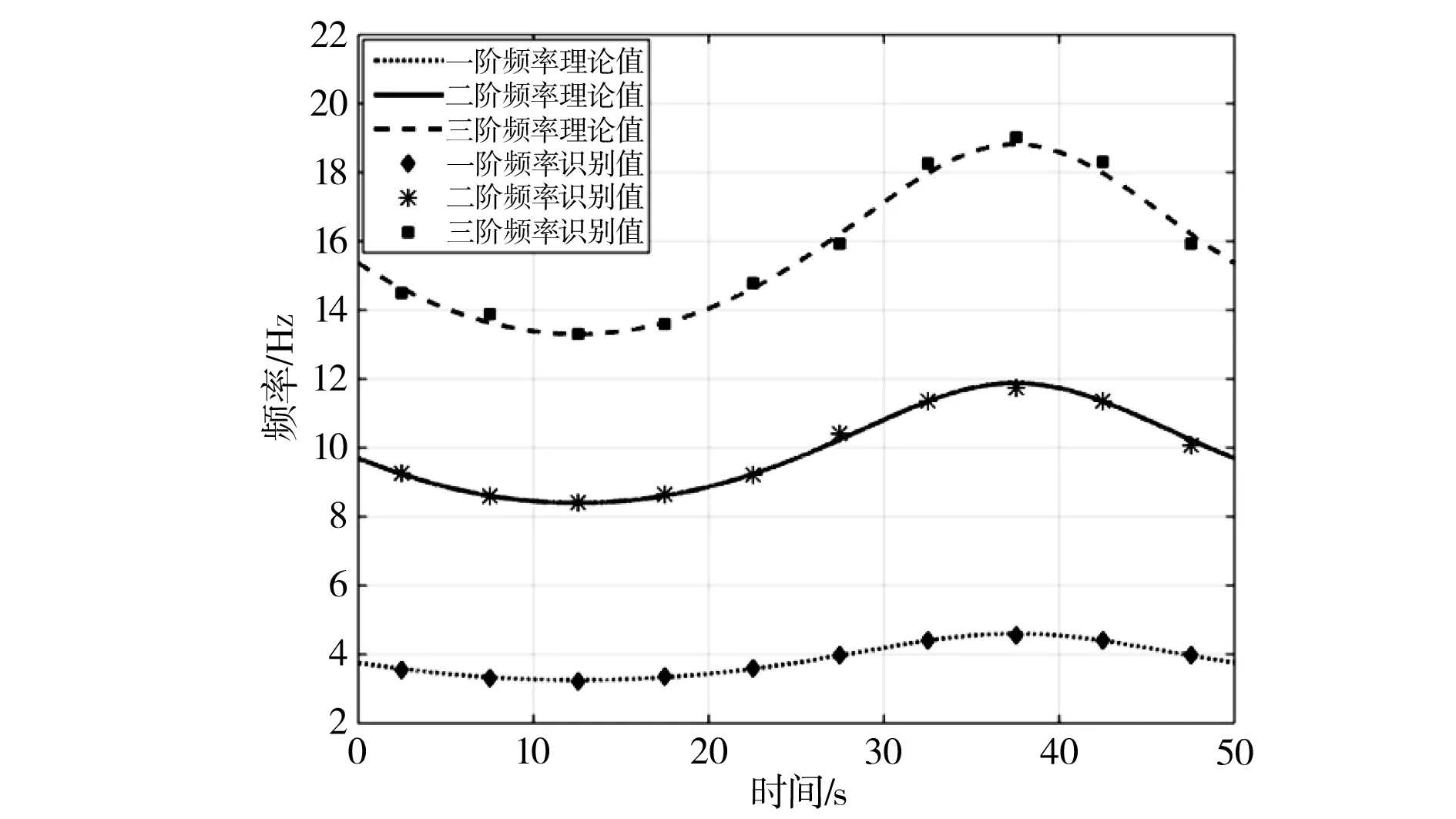
图6 结构三阶模态频率理论与识别结果对比
4 热环境下结构模态测试
切尖三角形翼面结构是现代高超声速飞行器常用的一种翼面结构形式,本文对一个钛合金三角翼结构进行了测试与分析。结构尺寸如下:根弦长1800mm,梢弦长150mm,半展长1200mm,前缘线与根弦的夹角为31°,厚度9mm。翼面结构的材料为TA15钛合金,试验件及夹具如图7所示。
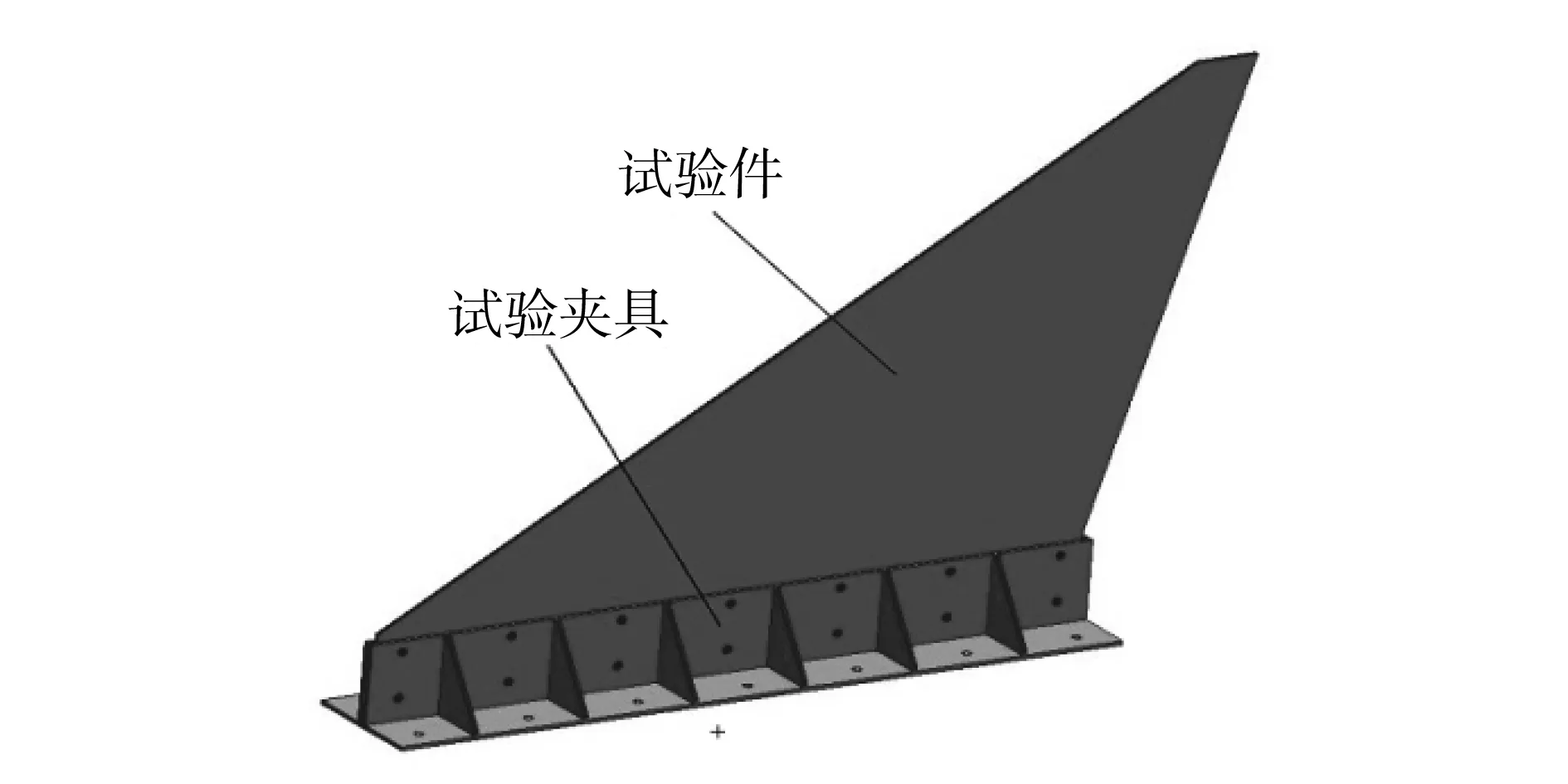
图7 试验件及夹具
为模拟气动加热效应,本文采用石英灯辐射加热的方式对试验件进行加热,同时将试验件划分为6个温区,模拟飞行器的温度分布。每个温区进行单独温度控制,试验件两面对称加热,结构温度分布及温控点布置如图8所示,试验加热现场如图9所示。
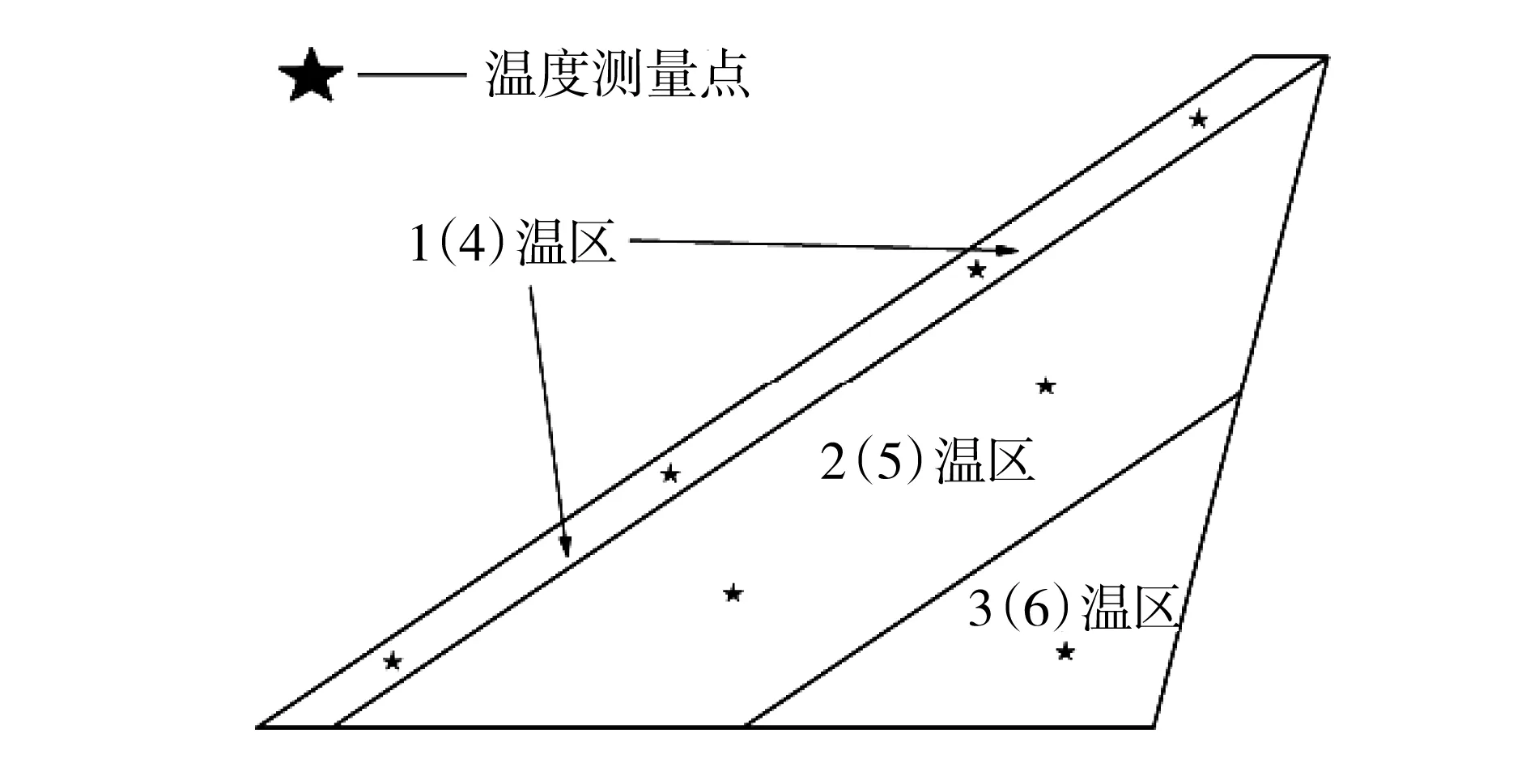
图8 结构温度分区

图9 试验加热现场
对6个温区进行独立温度控制,试验中最高温度为500℃,总加温时长为200s。图10给出了1#温区预设的温升曲线和实际温升曲线,可以看出,实际温升与预设值吻合很好。

图10 预设温升与实际温升对比(1#温区)
为了对高温环境下结构的振动特性进行测试,本文采用激振器对试验件进行激励。激励采用白噪声信号,利用激光测振仪测试结构响应,记录结构的响应速度信号,并通过对速度信号进行Chirp-Z变换获得结构的细化频谱特性,利用模态参数识别方法获得结构的振动特性参数。图11为测试获得的结构速度响应信号。
图11 测试结构速度响应时域信号
利用Chirp-Z变换对响应信号进行处理,设置分析频率带宽,分析获得结构的频率变化情况,图12给出了结构三阶频率识别结果。从图中可以看出,结构前三阶模态频率在加热过程中一直下降,而气动加热会从两个方面对结构的振动特性产生影响:(1)结构材料模量的下降;(2)结构内应力分布不均。一般来讲,结构模量下降会使得频率下降,结构内应力分布不均会导致结构模态频率升高,部分情况下会导致结构频率下降。
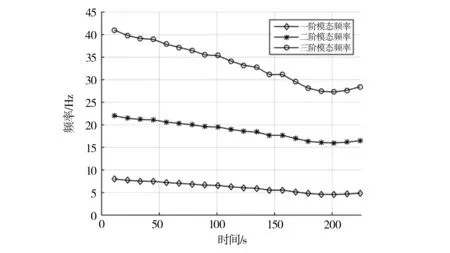
图12 结构前三阶模态频率随时间变化情况
5 结 论
本文采用Chirp-Z变换实现了受热结构的结构动态参数识别,有效解决了短时傅里叶变换的时间分辨率和频率分辨率的矛盾问题,为受热结构动态特性测试参数识别提供了一种有效方法,具体结论如下:
(1)与傅里叶分析相比,在相同时间序列长度情况下,Chirp-Z变换可以得到更加精细的频响特性,因此频率分析精度更高;
(2)Chirp-Z变换基于FFT技术,可以利用现有的FFT加速算法,因此具有较高的计算效率;
(3)对于时变结构,Chirp-Z变换可以不必增加采样点数即可提高频率分辨率、频率、幅值及相位精度,非常适合瞬态和短样本信号的频率细化;
(4)由于Chirp-Z变换需要一定的数据长度计算频谱数据,因此该方法仅适用于缓变信号,不适用于突变信号。

