附加不同竖直颤动下表面内能变化导致的热毛细对流界面响应行为研究
杨 硕,周晓峰,邓乔声,王国峰
(沈阳工程学院 辽宁省洁净燃烧发电与供热技术重点实验室,沈阳 110136)
与地面环境相比,许多地球上难以获得或无法获得的深空环境包含了大量有待探索的物理、化学和生命科学问题,并由此形成了一批前沿学科——微重力科学。这一新兴学科和前沿课题的发展又孕育了新型空间高技术产业的诞生。人类在“深空”极端环境方面的涉足为制备高质量、大尺寸半导体元件提供了可能。如何掌握深空极端环境材料生长过程背后的微重力流体物理传热与传质规律,成为多相流物理学基础研究中亟待解决的重要课题。2020年前后,我国将建成载人空间站核心舱与实验舱,其中已规划的微重力流体物理实验平台为空间微重力极端环境下毛细对流和界面现象的研究创造了有力条件。虽然深空环境下,重力水平被极大削弱(表面张力梯度引起的对流运动突显),但由于空间辐射、飞船姿态调整等因素产生的重力跳动和残余应力仍然存在,周期性颤动的体积力使得胞元流产生相应的运动和热力学参数变化,并影响毛细对流系统界面形状,流动平衡和运动规律。已有空间实验表明:重力跳动和残余应力效应与振荡热毛细对流频率相关。高频重力颤动作用下,热毛细对流系统的响应时间远大于重力颤动的固有周期,在一定控制参数下,其对热毛细对流自发振荡行为将产生积极作用。因此,研究重力颤动对热毛细对流系统的影响及其响应机制,有效利用这种作用减缓非平衡态热毛细对流不稳定性具有重要意义。
2005年,Kanashima等[1]研究了重力颤动对液桥中振荡热毛细对流引起的动态表面形变的影响。在压电驱动器驱动的振动实验台上模拟重力颤动施加的振幅和频率,并利用微成像位移计测量重力颤动下的界面变形。结果表明:重力颤动引起的振荡热毛细对流自由面变形按频率可划分为谐波和非谐波。Ichikawa等[2]基于“massspring-damper”模型,考察水平横向颤动下液桥毛细对流及界面响应行为,数值结果与“SpaceLab D-1”空间实验结果吻合。Liu等[3]采用线性不稳定性分析方法,研究了在高频颤动下2层流体系统中Rayleigh-Marangoni-Benard对流的不稳定性。结果表明:高频热动可以改变2层流体系统中Marangoni-Benard对流的不稳定性和Rayleigh-Marangoni-Benard振荡间隙。垂直高频振动可以延迟对流不稳定性,抑制对流向下流动。Liang等[4]用数值方法研究了绝热条件下单向以及多向颤动对三维液桥表面波的影响,外加横向颤动的频率达到反响频率时,可以完全控制液桥表面水平方向的振动。Kawaji等[5]利用level set方法数值捕捉附加重力颤动条件下三维液桥毛细对流的界面行为,并进行液桥共振频率的预测,数值结果表明:共振频率是随着液桥高度、直径以及密度的增加而减小,随表面张力的增加而增大,这一结果与Ichikawa等预测结论相一致。2014年,Lyubimova等[6]基于广义Boussinesq近似,研究高频竖直颤动对轴对称半浮区热毛细流动的影响及其三维扰动的线性稳定性。采用有限差分法在不同Weber数(We)下计算振动幅值和普朗特数对系统的影响。结果表明:竖直颤动可用来控制并降低流动强度,使流动稳定。2016年,Lyubimova等[7]研究外加高频微小竖直颤动对具有恒定垂直热通量的2层不相溶流体稳定性的影响。结果表明:长波不稳定性不受小、中等强度颤动的影响。当颤动瑞利数足够大时,单调有限波长扰动会加剧破坏2层流体系统的稳定性。Vjatkin等[8]在实验和理论上研究了转动频率和振动频率接近时,横向颤动对旋转圆柱空腔内非等温流体对流的影响。研究表明:横向颤动是控制旋转系统热对流的有效手段。当颤动频率接近旋转频率时,对流受到激发并加剧热传递。在一定频率下,非等温流体柱内发生二维方位角共振,并导致中心轴处的温度明显降低。热传递明显依赖于共振液体的振荡及频率。Kovskaya等[9]研究高频水平简谐颤动对带有自由表面的液层热毛细对流的影响。结果表明:颤动的纵向分量对热毛细对流不稳定性没有影响。如果稳定持续的颤动同时包含横向分量,则竖直颤动具有抑制热毛细对流不稳定性的很好效果。Kovskaya等[10]研究竖直颤动对具有自由表面不可压缩均匀流体液层Marangoni对流的影响。得到3个主要失稳类型的临界失稳参数方程,相应地同步参数共振域、次谐波,以及高频渐近形式的频率值被确定。研究表明:在竖直颤动下长波振荡Marangoni对流的Ma数只依赖于Pr数和Biot数(Bi)。
将空气域与液桥区形成的两相自由界面动力学形变及周围空气的影响考虑进来,模拟残余重力颤动及微重力环境,数值研究高Pr数液桥热毛细对流胞元流受迫运动规律,对于大密度比及高黏度比为流体介质的液桥热毛细对流,采用质量完全守恒水平集方法追踪气液界面响应行为。
1 物理模型
1.1 控制方程
本文研究对象的几何模型如图1所示,液桥半径和高度分别为R和H,置于2个轴对称圆盘的中间,上、下圆盘的温度分别为高温Tt及低温Tb,温差为ΔT=Tt-Tb。液桥周围被空气包围,气相区域的外径为2R。FGX为附加重力颤动力,微重力条件下竖直方向重力场加速度g=0 m/s2(液桥系统内浮力效应导致的浮力对流被忽略)。为考察自由界面在竖直颤动下的反响行为,参考系原点设置在液桥左侧空气域最左侧边界处。
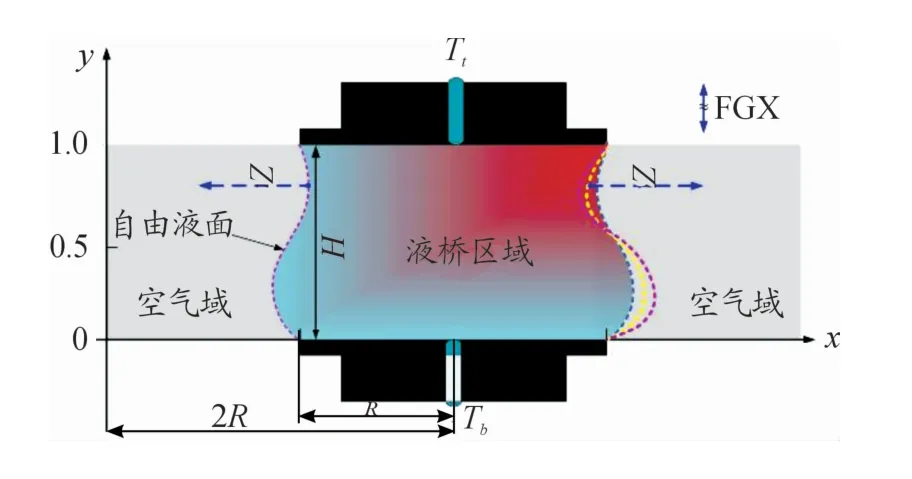
图1 带有竖直颤动的半浮区液桥坐标系统
由以下无量纲化的质量守恒方程,Navier-Stokes方程和能量守恒控制方程描述本文的研究对象。
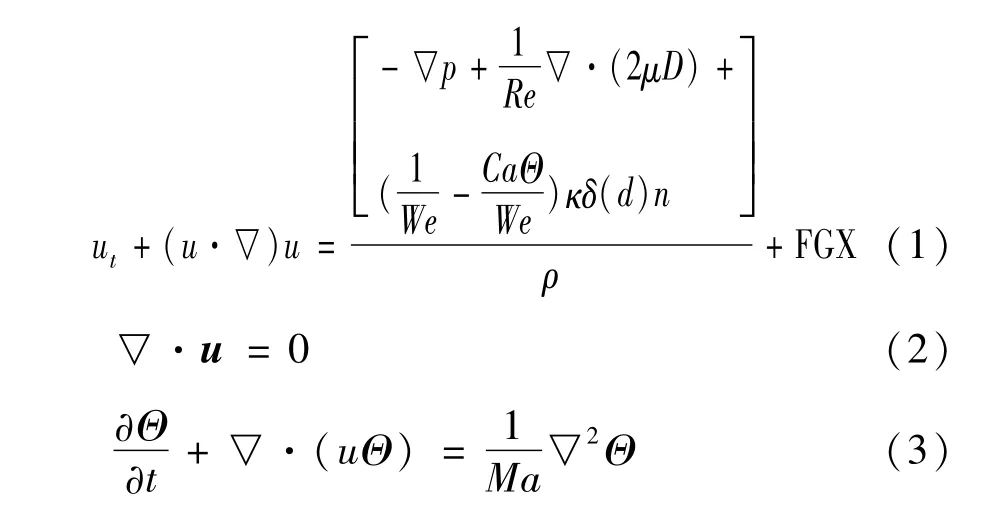
式中:u=(u,v)为流体流速;ρ=ρ(x,t)为流体密度;μ=μ(x,t)为流体动力黏度;D是黏性应力张量;κ是自由界面的曲率;d为计算质点到界面的法向距离;δ为狄拉克函数(δ(x)=0,x≠0),;n为界面处的单位法向矢量;t为时间项;P为压力项。
表面张力系数被看作是温度的线性函数,表示为σ=σc-σT(T-Tb);其中,σc是环境温度下(T0=25℃)表面张力的参考值;σT是表面张力的温度系数;σT=∂σ/∂T,T为界面流温度。FGX是由附加重力颤动引起的外力是y轴方向上的外部加速度,A是颤动幅度,ω角频率(ω=2πf);f为颤动频率,为特征长度,定义特征长度=D,其中D为液桥的初始直径。U∞是特征速度则微重力下,有为无量纲时间,表示为。此外,本课题组认为液桥介质为不可压缩牛顿流体,对连续性方程、动量方程和能量方程采用Boussinesq近似。
在表面内能变化数值研究方面,将界面形状特性和温度特性差异完整引入界面内能变化,
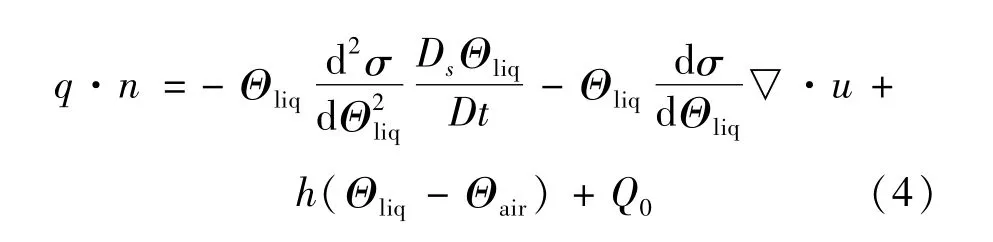
式中:σ为液桥自由界面表面张力;Θliq为非等温液桥自由表面温度;Θair为环境侧温度;Q0为由非等温液桥侧向环境侧的热通量。(4)中等号右侧第1项表征界面温度引起的表面内能变化项;第2项表征自由面形变导致的表面内能变化项。其他无量纲参数定义如下:和分别对应环境空气区域内的无量纲密度比和动力黏度比;ρl和μl分别是液桥区域流体介质的密度和动力黏度;ρg和μg分别是环境空气域内流体介质的密度和动力黏度。液桥内部流体介质的无量纲密度比(ρl/ρl)和无量纲黏度比(μl/μl)均等于1。雷诺数定义为;韦伯数定义为We=;普朗特数定义为Pr=μl/ρla;热毛细数定义为Ca=μlU∞/σ,热Marangoni数定义为Ma==RePr,绝对温度的无量纲形式为Θ=(T-Tb)/ΔT;a是热扩散率。
1.2 水平集方法及重整化处理
水平集方法最初是由Osher等[11]提出,用于数值预测两相流体介质之间的运动界面。Level set方法在整个计算域内隐式跟踪运动界面。在水平集方法中,ϕ(x,t)代表两相界面函数,液桥界面空气域ϕ(x,t)>0,液桥界面处为ϕ(x,t)=0,液桥界面内部ϕ(x,t)<0。通过求解Level set函数ϕ(x,t)可以预测界面的运动位置。

基于上面对液桥界面内外介质密度和黏度的处理,结合Level set函数界面位置,流场中的密度函数ρ(ϕ)、黏度函数μ(ϕ)和Heaviside函数可以分别表示为:
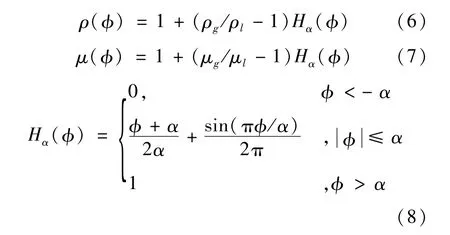
其中,为避免求解过程中界面附近密度和黏度阶跃性变化带来的计算不稳定性,在计算中选取α=2.0Δx,α表示液-气界面厚度,Δx是x方向上的网格距离。
为避免Level set函数求解过程中自身带来的质量失衡,Sussman等[12]提出采用方程(9)(10)来实现Level set函数重新初始化。

式中:ϕ0(x)和ϕ(x)有着相同的水平集数。然而即使采用重新初始化程序,总质量在时间尺度上仍然不能完全满足完全的质量守恒。这主要是由于水平集函数数值离散过程中自身的缺陷,为克服计算失真问题,质量守恒过程必须通过求解如下面积补偿(二维模型)方程来实现。

式中:A(t)是水平集函数ϕ(t)在时间t时所对应的液桥面积(二维模型),A0是初始条件下液桥的初始面积。面积约束函数F(c)的定义如下:

F(c)随着h和n的变化而变化,当h=0和n=0时,数值计算过程的收敛速度会更快,收敛性的判别条件如下:
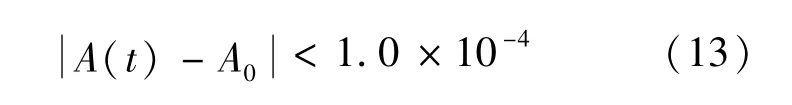
1.3 边界条件和初始条件
计算区域所有的边界均假设为绝热壁面(除液桥的热盘、冷盘和自由界面之外),热盘和冷盘的初始温度分别保持为Tt和Tb(随后保持恒定的升温速率),温差为ΔT,满足边界条件如下:

本文所研究的两相系统中,需要考虑初始静止状态和液桥周围空气的初始速度。
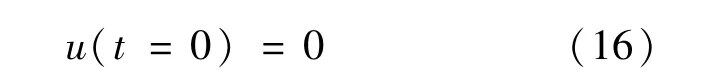
无滑移边界条件同样适用于液桥上、下盘。

采用质量守恒水平集法分析液桥的自由界面运动,在交错网格上求解Navier-Stokes方程和能量守恒方程,对平流项采用QUICK迎风插值法进行离散,对其他项采用中心有限差分法进行离散,对时间积分项采用2阶Adams-Bashforth方法离散。
对于表面张力的求解计算中采用CSF(continuum surface force)方法。假设在液桥自由界面上表面张力连续分布,由Level Set函数可以将表面张力项表示为:
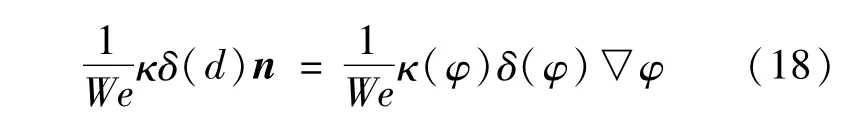
其中,界面曲率κ(φ)由κ(φ)=-▽·(n)和▽·n=▽·确定。
2 对比验证
为了验证本文模型的正确性,将液桥内部等温线计算结果与Shevtsova等[13]的数值结果进行比较。在零重力场条件下,以10 cSt硅油液桥作为验证对象(R=3 mm,H=4 mm,ΔT=40 K,Re=166,Pr=105)。如图2所示,计算结果与Shevtsova等的结果(b)较为吻合,但本文的计算方法考虑了液桥自由界面的动态变形过程。

图2 数值方法的对比验证(Pr=105,Re=166,Γ=R/h=4/3)
3 竖直颤动对胞元流涡心位置及自由界面行为的影响
3.1 竖直颤动下胞元流涡心在轴向上的位置变化
为了研究微重力条件下竖直颤动对液桥表面以及内部热毛细对流胞元流产生的作用,设定附加垂直颤动力为20 mg(FGX),并分别选取颤动频率f=0 Hz,f=5 Hz,f=20 Hz进行模拟。在数值计算中,液桥介质选用5cSt硅油:Re=320,Ma=22 037,We=3.5,Pr=66.93,Ca=5,上、下圆盘的初始温差为ΔT=25℃,气相、液相的密度比和黏度比分别为ρg/ρl=1.35×10-3和μg/μl=5.528×10-3,其他物性参数见表1。
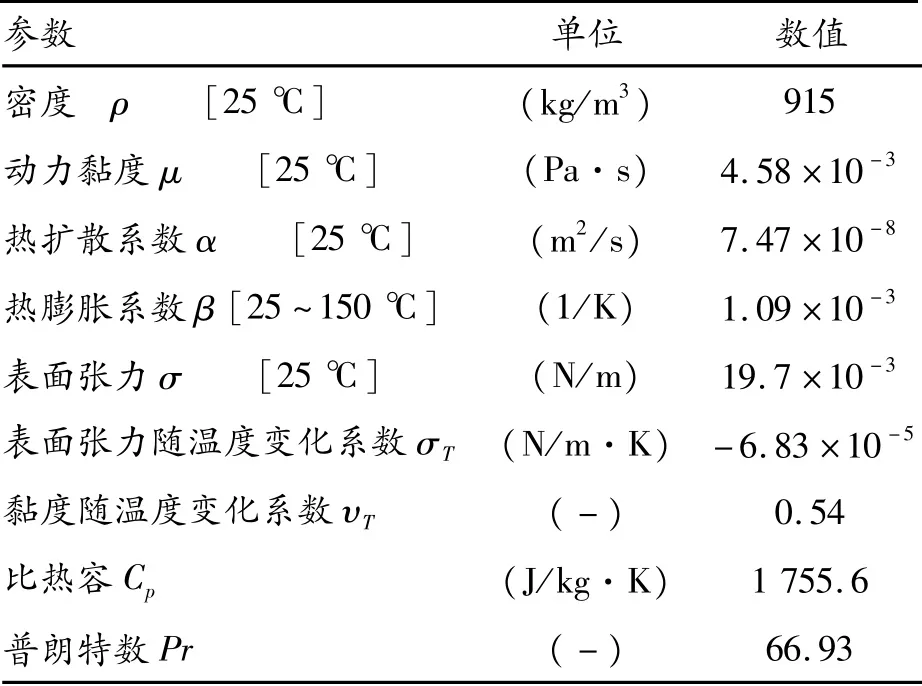
表1 5cSt硅油物性参数
图3给出了数值结果分析中液桥几何位置关系的主要信息。本文建立的计算域原点并不在液桥的中轴线上(如图1所示),但研究对象为稳定热毛细对流,热毛细对流的胞元流型态呈现轴对称特征,下文中为了简化表达只给出了一半液桥的数值结果。
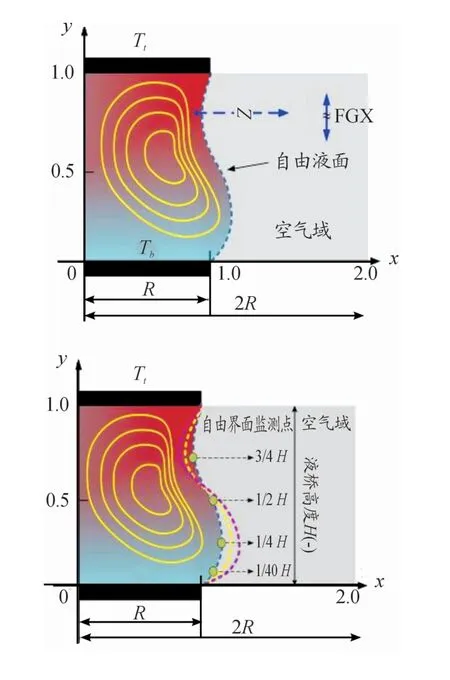
图3 计算模型的几何位置关系
以液桥区域流函数绝对值的最大值作为捕捉涡心位置的判据,流函数绝对值的变化意味着涡心位置的变化。在没有施加竖直颤动的情况下(f=0 Hz),涡心位置随热毛细对流发展,涡心存在自发性的摆动,如图4所示(f=0 Hz)。在不同频率外加颤动的作用下(f=5 Hz,f=20 Hz),液桥热毛细对流胞元流涡心位置在轴向上的变化如图4所示,施加的竖直颤动加速度水平相同,均为20 mg。图4(a)(b)分别表示初始阶段胞元流涡心位置的变化和颤动后期胞元流涡心位置的变化,y轴表示涡心距冷端(下盘)的纵向无量纲距离。由于热毛细对流首先在热角发起,所以初始时刻涡心高度位于热角附近,且总体摆动幅度较大(最大摆动幅度(Amax=0.25)。外加颤动对流动在轴向方向上产生影响,使热毛细对流在轴向上受到抑制。在经过初始阶段后,热角区的活跃性逐渐减弱,胞元流涡心逐步向冷端移动,并处于稳定的小振幅状态(最大摆动幅度Amax=0.10),颤动状态下的平衡位置如图4(b),且围绕着某一平衡位置为上限(y=0.55)进行周期性波动。但无论是在“初始阶段”还是“稳定阶段”,随着竖直颤动频率的增加,热毛细对流胞元流涡心位置轴向摆动幅度逐渐减小。
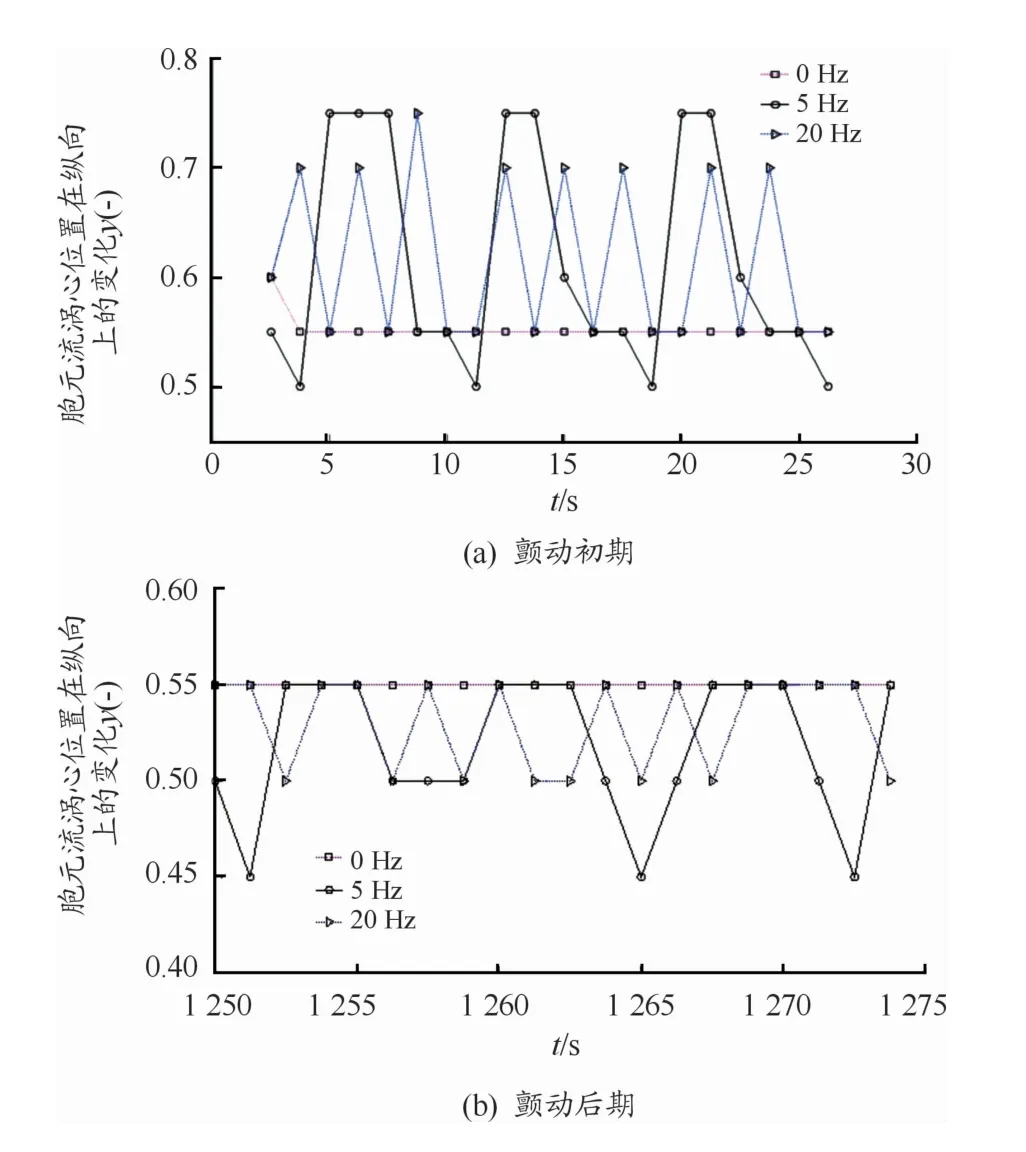
图4 竖直颤动频率对胞元流涡心轴向位置的影响曲线(Pr=66.93,Ma=22 037,FGX=20 mg)
3.2 竖直颤动下胞元流涡心在径向上的位置变化
如图5所示,热毛细对流胞元流的涡心在竖直颤动力的作用下,不仅影响涡心在轴向上的位置分布,还会影响其在径向上的位置分布。图5(a)和图5(b)分别为胞元流涡心径向位置在“初始阶段”和“稳定阶段”的分布。在初始阶段,当没有附加竖直颤动力时(f=0 Hz)涡心径向位置稳定的位于R=0.6处(R为液桥无量纲半径)。随着竖直颤动频率的增加(f=5 Hz,f=20 Hz),涡心径向位置围绕着R=0.6处进行周期性不规则摆动。竖直颤动频率为f=20 Hz时,涡心径向位置摆动幅度加剧。在稳定阶段,涡心径向位置呈现周期性的摆动特点,并且摆动的下限维持在R=0.55处,与未施加竖直颤动力相比,涡心径向位置摆动的上限仍然维持在R=0.60。从图5可知,附加竖直颤动会迫使胞元流涡心径向位置呈现稳定性的周期摆动,且摆动周期随颤动频率的增加而减小。
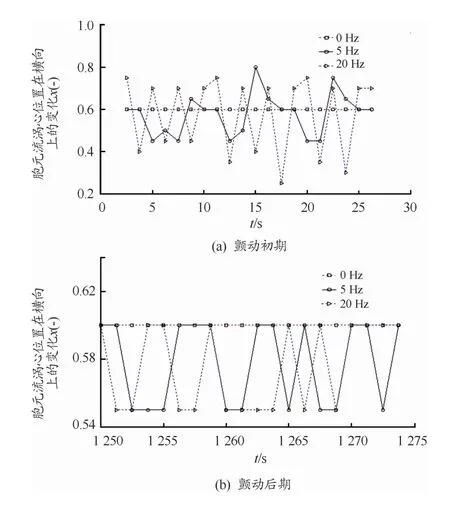
图5 竖直颤动频率对胞元流涡心径向位置的影响曲线(Pr=66.93,Ma=22 037,FGX=20 mg)
3.3 附加竖直颤动下液桥自由界面波动的响应行为
竖直颤动会引起液桥自由界面产生微弱的高频振荡,并与胞元流涡心轴向和径向上的摆动共同构成竖直颤动下复杂热毛细对流流动结构演化行为,在以往的研究中这种变形很难从实验中直接定量观察。在竖直正弦颤动频率f=0、5、20 Hz下,分别选取液桥表面上距离冷端(下盘)垂直高度1/40H、1/4H、1/2H、3/4H处作为监测点,定量考察自由界面横向位置摆动(如图6所示),图中y轴表示液桥自由界面横向位置偏离液桥半径的变化量。

图6 竖直颤动频率对自由界面不同高度处表面横向位置振幅的影响曲线(Pr=66.93,Re=320,Ma=22 037,FGX=20 mg)
从图6(a)中可以看出:未加入竖直颤动情况下(f=0 Hz),液桥自由界面横向位置存在微弱的大周期摆动,但是随着时间的推移,液桥表面横向位置振幅逐渐稳定,且A1/2H=1.5×10-4>A3/4H=1.2×10-4>A1/4H=1.0×10-4>A1/40H=0(中间高位置处自由界面横向位置偏离原始位置R最大),这与热毛细对流胞元流的发展、壮大以及涡心游动有关;施加竖直颤动频率为5、20 Hz情况下(如图6(b)(c)所示),自由界面横向位置呈现出周期性明显的摆动。在竖直颤动频率f=5 Hz情况下,液桥表面高度1/40H处自由界面横向位置没有发生颤动。液桥界面高度1/4H处自由面横向位置的振幅ΔAm=0.5,周期为TAm=25。液桥表面高度1/2H处自由界面横向位置振幅最小。液桥表面高度3/4H处自由界面横向位置的振幅均大于其他位置(ΔAm=0.7,TAm=25);与f=5 Hz相比,在竖直颤动频率f=20 Hz情况下,液桥自由界面横向位置脉动性摆动明显,自由界面横向位置振幅的大小关系如下,ΔA3/4H>ΔA1/4H>ΔA1/2H>ΔA1/40H。综上所述,随着竖直颤动频率的增加,自由界面横向位置的摆动周期减小,振幅基本没有改变。
3.4 附加竖直颤动下液桥自由界面轴向和径向速度的响应行为
液桥自由界面表面流的轴向速度分量如图7所示。轴向速度分量v为正,表示速度方向与y轴正向一致;轴向速度分量v为负,表示与y轴负向一致,液桥表面流由热角(上盘)流向冷角(下盘)。
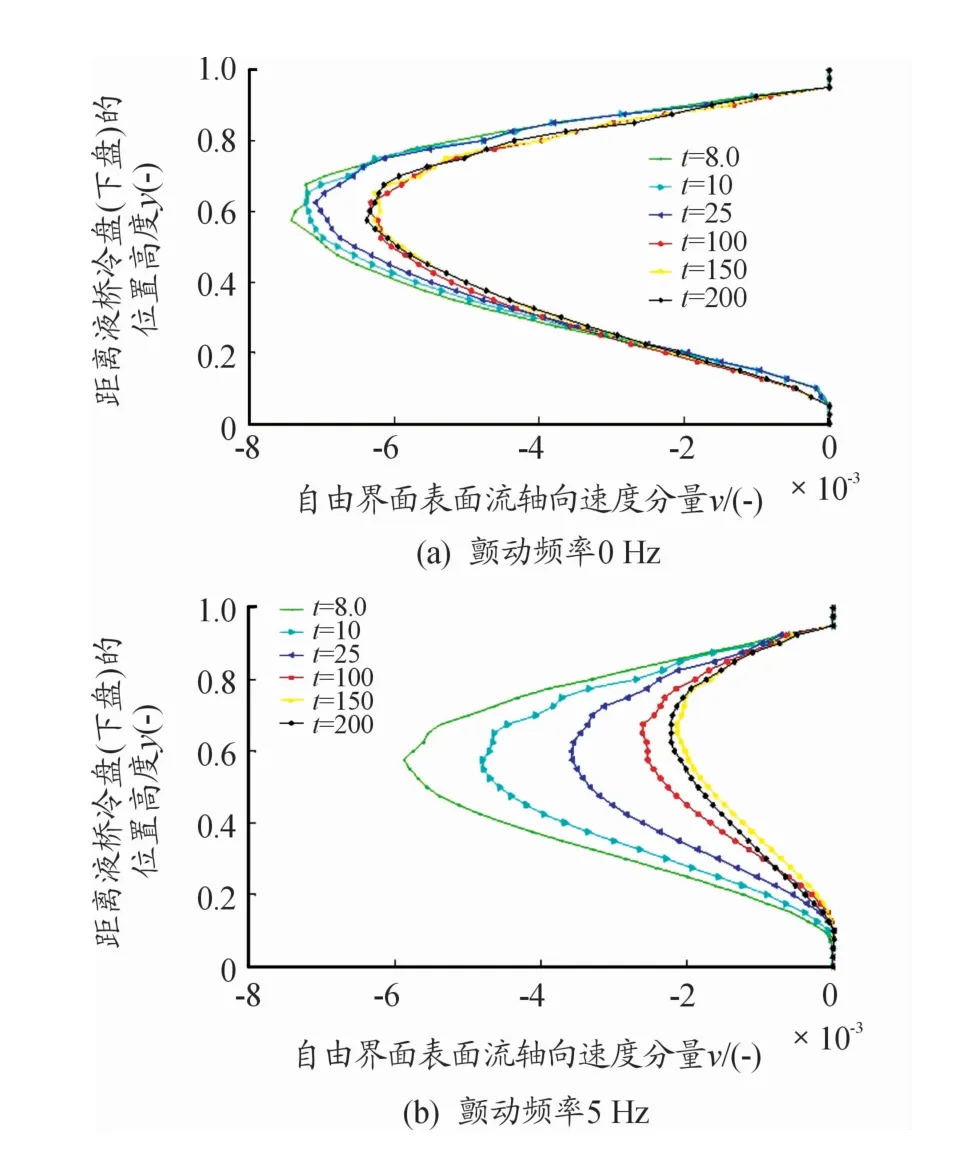
图7 直颤动频率对自由界面表面流轴向速度分量的影响曲线(Pr=66.93,Re=320,Ma=22 037,FGX=20 mg)
在没有施加竖直颤动情况下(f=0 Hz,如图8(a)所示),初始阶段t=8~25 s的轴向速度v值较大,随着热毛细对流的发展和涡心的游动,t=100~200 s时刻的轴向速度逐渐衰减;相对于初始阶段,t=100~200 s阶段液桥内的热毛细对流已接近稳定流动。在施加竖直颤动频率f=5 Hz情况下(如图7(b)所示),液桥表面流轴向速度v明显衰减,最大衰减幅度达Δv=3.5×10-3,这说明竖直颤动力的施加抑制了液桥自由界面表面流轴向速度向冷端(下盘)的发展。
液桥自由界面表面流的径向速度分量如图8所示,径向速度分量u为正,表示速度方向与x轴正向一致,说明表面流由液桥中心流向界面;径向速度分量u为负,表示速度方向与x轴负向一致,说明表面流由界面流向液桥中心。
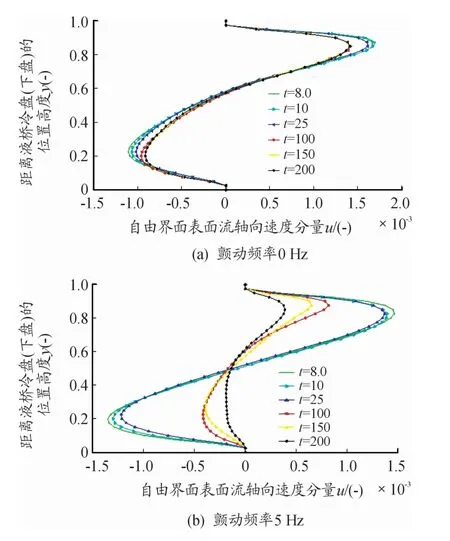
图8 竖直颤动频率对自由界面表面流径向速度分量的影响曲线(Pr=66.93,Re=320,Ma=22 037,FGX=20 mg)
如图8(a)所示,液桥自由界面表面流径向速度u在距冷端无量纲距离y=0.55以上为正,在液桥自由界面高度y=0.0~0.55范围内,表面流径向速度u为负,即液桥表面流径向速度在靠近热角处为正(上盘),靠近冷角处为负(下盘),且径向速度峰值分别位于y=0.9和y=0.2。同表面流轴向速度表现相近,初始阶段(t=8~25 s)的速度波动范围较大,而在稳定阶段(t=100~200 s)速度波动范围明显变小。在附加竖直颤动力频率为f=5 Hz情况下(如图8(b)所示),随着频率增加径向速度减小,且稳定阶段(t=100~200 s)径向速度明显小于未施加竖直颤动下的径向速度,最大衰减幅度达Δu=1.0×10-3。
3.5 附加竖直颤动下液桥自由界面位形的响应行为
图9为附加竖直颤动20 mg、20 Hz条件下,液桥自由界面位形的变化情况,选取液桥右半部分作为分析对象(如图3所示),左半部分为液桥域,右半部分为空气域,从图9中可以看出:在无量纲时间t=860~864 s,液桥自由界面高度y=0.45~1.0部分的表面逐渐向液侧收缩;在时间段t=866~870 s,液桥自由界面高度y=0.45~1.0部分的表面逐渐向气侧扩张。与此同时,液桥冷端处表面(y=0~0.45)向液侧收缩。因而,液桥自由界面在附加竖直颤动力作用下,液桥近热端和近冷端的表面呈现交替状的扩张和收缩,且上、下2部分的转折点距冷端的无量纲距离为y=0.45,不在液桥的中间高位置y=0.5。
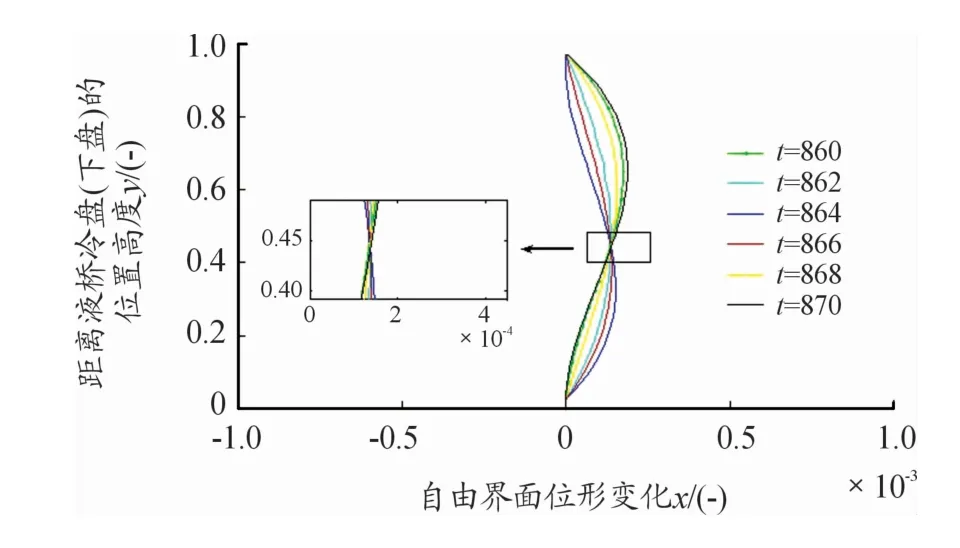
图9 竖直颤动对液桥自由界面位形的影响曲线(Pr=66.93,Re=320,Ma=22 037,FGX=20 mg,f=20 Hz)
4 结论
1)竖直颤动对热毛细对流胞元流的作用可以由胞元流涡心轴向和径向位置的变化体现。无论是在“初始阶段”还是“稳定阶段”,随着竖直颤动频率的增加(f=0 Hz→f=5 Hz→f=20 Hz),涡心存在的自发性摆动受到抑制,热毛细对流胞元流涡心位置轴向摆动幅度逐渐减小,最大摆动幅度由ΔAmax=0.25衰减至ΔAmax=0.10。受竖直颤动的影响,胞元流涡心径向位置由原来无规则摆动呈现出稳定性的周期摆动,且摆动周期逐渐减小。
2)随着竖直颤动频率的增加,液桥自由界面横向位置的摆动周期减小,振幅基本没有改变,脉动特性明显。在竖直颤动频率20 Hz情况下,自由界面横向位置振幅的大小呈如下排布,ΔA3/4H>ΔA1/4H>ΔA1/2H>ΔA1/40H。
3)竖直颤动对液桥自由界面表面流速度的影响:竖直颤动力能够抑制液桥自由界面表面流轴向速度向冷端(下盘)发展。随着竖直颤动频率的增加,稳定阶段(t=100~200 s)径向速度明显减小,且最大衰减幅度达Δu=1.0×10-3。
4)在竖直颤动力的作用下,液桥近热端(y=0.45~1.0)和近冷端(y=0~0.45)的表面呈现交替性的扩张和收缩。

