融合多源数据的区域动态协调信号控制
徐震辉,邵 庆,应东辉,刘 畅,胡灵龙,刘 志
(1.浙江浙大中控信息技术有限公司,浙江 杭州 310053;2.杭州市公安局萧山区分局交通警察大队,浙江 杭州 311200;3.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
随着城市规模的扩大、路网密度的增加以及交通需求的增长,交叉口之间的交通流相关性日益明显。为提高区域交通运行的整体效率,需要打破单路口控制的局限,从城市路网总体控制目标出发,统筹协调交叉口群的信号配时方案。在“互联网+”和大数据的背景下,交通数据越来越丰富,每天都有海量实时的动态数据生成,给动态交通信号控制带来了崭新的生命力,也产生了数据存储格式不统一、采集频率不统一和质量参差不齐等问题。通过多源数据融合[1]准确地获取交通参数,识别与预测交通态势,进行交通信号控制决策,实现自适应动态协调控制,已经成为交通信号控制技术的主流趋势[2-3]。徐涛等[4]采用贝叶斯估计和模糊逻辑等数据融合方法,针对多源异构交通信息,建立了数据级、特征级和决策级3 个层次的融合体系。于超等[5]以视频检测和微波检测数据为基础, 结合BP神经网络模型,对城市信号控制主干道的旅行时间进行预测。唐克双等[6]基于对定点线圈、浮动车和AVI数据的融合,进行城市道路交通状态估计与判别,实现交叉口单点信号控制和城市干道协调信号控制。Wang等[7]利用手机信令数据和出租车GPS数据定位瓶颈路段车辆的主要来源,筛选需要进行信号优化的交叉口,实施瓶颈控制,缓解交通拥堵。
在上述研究的基础上,笔者提出一种融合多源数据的区域动态协调信号控制算法,利用基于置信度的多源数据融合技术,从交通特征参数挖掘入手,采用模糊规则和马尔可夫链模型实现对交通态势的识别与预测,并将宏观战略决策与微观战术决策相结合,生成区域协调控制方案,以提高区域信号控制的响应能力和智能决策水平。
1 算法总体框架
算法包括两个模块:数据融合与态势识别模块和区域动态协调信号控制算法模块,其总体框架图如图1所示。数据融合与态势识别模块首先对传统交通检测数据和互联网数据进行重构,并基于置信度标签进行多源数据融合,然后利用融合数据计算交通态势强度指数,预测交通态势等级,识别畅通、缓行和拥挤3 个交通态势。区域动态协调信号控制算法模块在每个优化间隔ΔT1(默认30 min)内,依据交通态势动态制定控制子区的协调策略,同时在每个优化间隔ΔT2(默认15 min)内依据流量、速度和协调策略等信息动态生成与实际交通态势相适应的控制方案,下发至路口信号机。信号机执行新方案后,又重复上述过程,如此循环,实现信号控制方案的迭代优化。
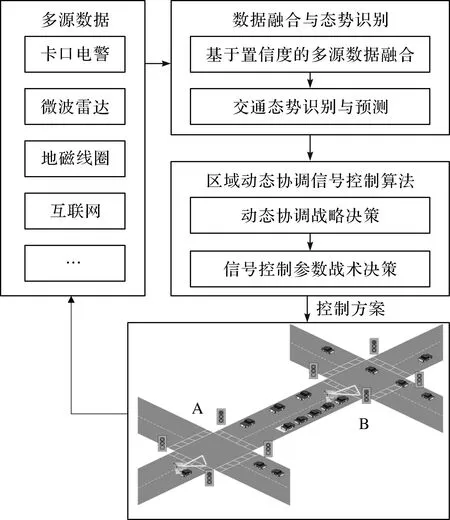
图1 融合多源数据的区域动态协调信号控制算法框架
2 多源数据融合与交通态势预测
2.1 多源数据融合
首先对多源数据进行重构,统一数据量纲和频率,提取交通流量、饱和流量、行程速度、协调速度和排队长度。行程速度指考虑路口红灯停车的速度,主要用于评价;协调速度指不考虑路口红灯停车的速度,主要用于优化相位差。在完成数据重构后,通过数据诊断识别异常值和缺失值,利用时空关联分析对数据进行修复[8]并标记数据的置信度。采用5级置信度标签为数据打分,5表示信任数据;4表示修复数据,置信度高;3表示修复数据,置信度中;2表示修复数据,置信度低;1表示未修复成功的数据,置信度极低。对不同来源的同一交通参数y,基于数据置信度进行多源数据的融合,步骤为
Step1在每个采样间隔内,判断所有数据源中是否有置信度标签为5的数据,如果有,进入Step 2;如果没有,进入Step 3。
Step2将置信度标签为5的多源数据取平均,作为融合后的数据。
Step3根据置信度标签为不同来源的数据赋予不同权重,将加权平均的数据作为融合后的数据,即
(1)
式中:f为第f个数据来源;yf为第f个数据来源中某一交通参数的值;αf为第f个数据来源的置信度标签。
2.2 交通态势识别与预测
利用融合后的交通参数,构建不同层级的交通强度指数,划分并预测交通态势等级,将交通态势分为畅通、缓行和拥挤等3 类,作为后续区域动态协调信号控制中协调策略的生成依据。交通态势识别与预测方法如图2所示。
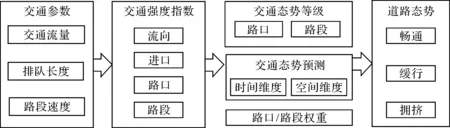
图2 交通态势识别与预测
路段交通强度指数的计算依赖于行程速度v,因路段两个方向的交通态势存在差异,在交通强度指数的计算中,以路段的一个交通通行方向为分析对象,即
(2)
式中:Pa为单向路段a的交通强度指数,取值为[0, 1];v为路段a的行程速度,km/h;vmax为路段a的自由流速度,是基于历史数据分时段分析得出的值,按固定频率更新,km/h。当出现车辆超速,即v>vmax时,取Pa=0。
路口交通强度指数以车道饱和度为基础,结合绿灯末排队长度计算。当路口状况良好时,饱和度足以反映交通态势;而随着拥堵加剧,车辆移动缓慢,检测到的过车数量减少,导致饱和度减小,无法准确反映交通态势变化,因此需结合排队长度进行综合判断。采用一种双输入单输出的模糊模块实现判别过程,输入为路口的各流向饱和度xk和各流向排队强度lk,输出为各流向交通强度指数Pk。其中,排队强度的计算式为
(3)
式中:Lqueue,k为流向k的排队长度;L为路段长度。
对xk,lk,Pk进行模糊子集定义:流向饱和度xk的基本论域为[0,1],语言值为VS(很小)、S(小)、LS(略小)、LB(略大)、B(大)、VB(很大),流向饱和度隶属度划分如图3所示;排队强度lk的基本论域为[0,1],语言值为VS(很小)、S(小)、B(大)、VB(很大),排队强度隶属度划分如图4所示;交通强度指数Pm,k的基本论域为[0,1],语言值为VW(很弱)、W(弱)、M(中)、S(强)、VS(很强),交通强度指数隶属度划分如图5所示。
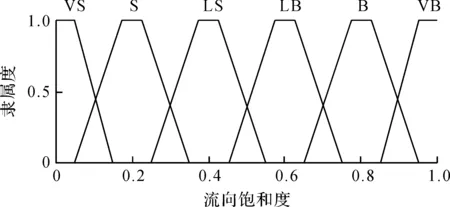
图3 流向饱和度隶属度划分
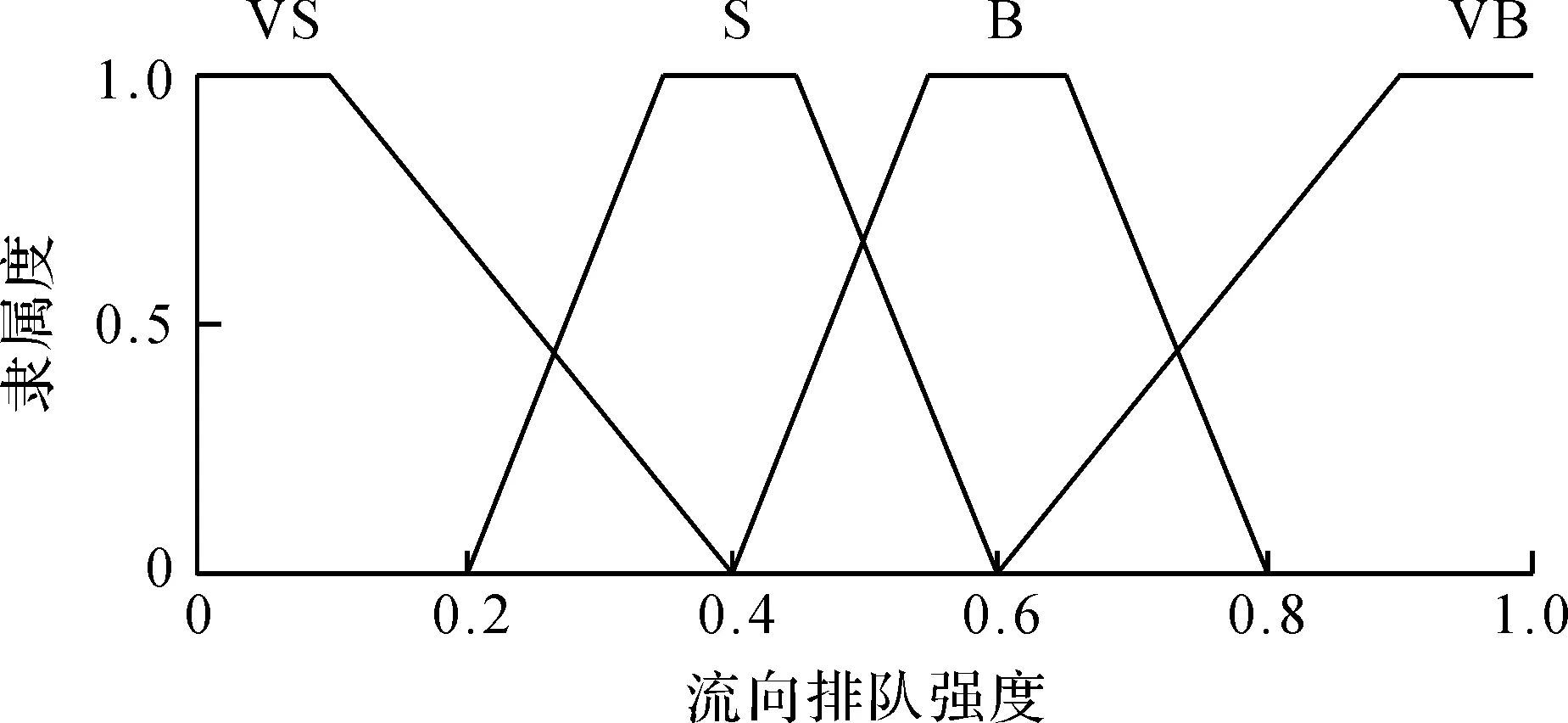
图4 排队强度隶属度划分
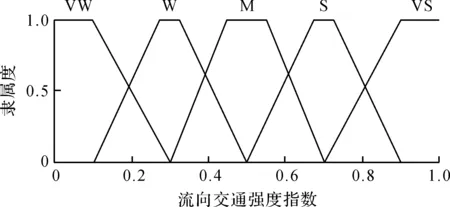
图5 交通强度指数隶属度划分
模糊规则为Pk与xk和lk正相关,即饱和度和排队强度越大,则交通强度指数越大。共有24 条模糊规则,如表1所示。
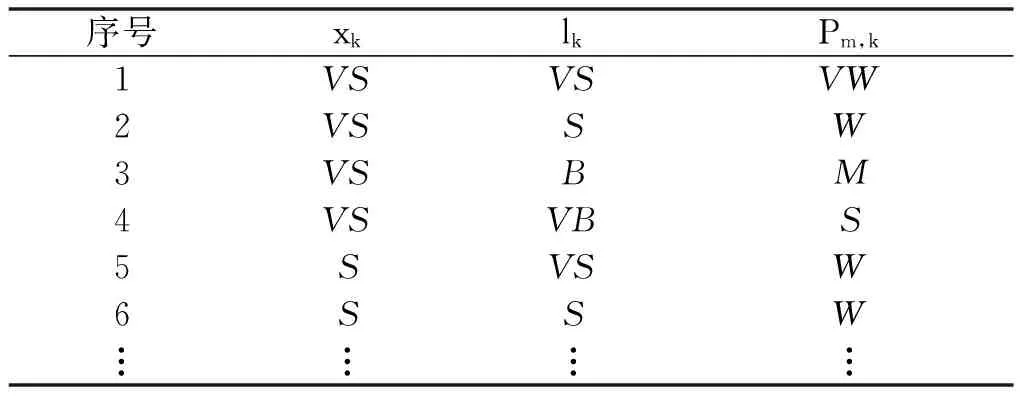
表1 模糊规则
在获得流向交通强度指数后,取进口中各流向交通强度指数最大值作为进口交通强度指数,并以进口所在道路的道路等级为权重,经过加权平均将进口交通强度指数处理为路口交通强度指数Pi。为便于后续预测,将上述交通强度指数P映射为10 级交通态势等级PL,映射关系如表2所示。

表2 交通强度指数与交通态势等级映射表
基于历史交通态势等级,从空间与时间两个维度对目标路口或路段交通态势等级进行预测。空间维度的预测利用路口和路段的空间相关性实现。路段下一时间间隔t+1的交通态势等级通过时间间隔t内其自身的交通态势等级和与其相连的路口进口的交通态势等级预测得到。路口下一时间间隔t+1的交通态势等级通过时间间隔t内其自身的交通态势等级和与其相连的进口路段的交通态势等级预测得到。以路口为例,计算式为

(4)
式中:PLi(t)为当前时间间隔t路口i的交通态势等级;PLa(t)为当前时间间隔t与路口i相连的进口路段a的交通态势等级;M为与路口相连的进口路段数;ωa为基于路段等级生成的各路段权重系数;PLi,space(t+1)为下一时间间隔t+1的基于空间维度预测的交通态势等级;β为算法参数。
时间维度的预测利用马尔可夫链模型[9]实现。基于当前时间间隔的交通态势等级和历史同期的交通态势变化趋势预测下一个时间间隔的交通态势等级,具体步骤为
Step1历史数据采集。获取历史交通态势等级的时间序列,将两个相邻时间间隔的交通态势等级组合为一个数据对。
Step2通过对历史数据中各个状态之间相互转换情况的统计,计算状态转移概率矩阵D。
Step3交通态势等级预测。设路口当前状态向量为Z(t),则下一时间间隔的状态向量为
Z(t+1)=Z(t)·D
(5)
取Z(t+1)中元素的最大值对应的交通态势等级作为下一时间间隔的交通态势等级预测PLi,time(t+1)。融合空间维度与时间维度的预测结果,生成路口和路段最终的交通态势等级预测值。综合道路协调方向上所包含的路口和单向路段交通态势等级,以道路等级和路口等级为权重,获得道路上行方向和下行方向的交通态势等级,映射为3 类交通态势:畅通、缓行和拥挤。设PLmin和PLmax为交通态势等级阈值,划分方法如下:PL≥PLmax时为拥挤;PLmin 区域动态协调信号控制算法主要包括两部分:宏观动态协调战略决策和微观信号控制战术决策。宏观动态协调的战略决策是根据交通需求的变化对交叉口群进行协调策略的动态优化,微观信号控制的战术决策[10]是基于当前的协调策略和交通需求,计算周期、绿信比和相位差,对配时方案进行动态优化。 在每个优化间隔ΔT1内,根据实时交通需求,判断上行和下行的交通态势,按照动态协调战略决策树选择相应的协调策略,实现协调策略对交通需求的动态响应。结合项目现场的实际应用需求,定义5类协调策略,以实时适应畅通、缓行和拥挤的交通控制场景:1)双向绿波;2)单向绿波;3)单向红波;4)一向红波一向绿波;5)双向红波。宏观动态协调战略决策树如图6所示。 图6 宏观动态协调战略决策树 3.2.1 周期优化 周期优化以关键路口为对象,以饱和度最匹配为目标。周期的合理性以路口饱和度来表征,若饱和度偏小,则周期偏大;若饱和度偏大,则周期偏小;若饱和度处在最佳区间,则周期合理。具体步骤为 Step1计算关键路口的饱和度,其计算式为 (6) (7) 式中:xi为路口i的饱和度;xj为相位j的饱和度;n为相位个数;qk为流向k的小时流量,veh/h;qs,k为流向k的小时饱和流量,veh/h;λj为相位j的绿信比。 Step2周期优化。为了防止周期突变引起交通流混乱,采取小步距的周期调整来适应渐变的交通流。计算式为 (8) 式中:Tout为优化后输入的周期值,s;Δt为周期调整步距,据现场应用经验取10 s;xmin为饱和度最小阈值;xmax为饱和度最大阈值。 3.2.2 绿信比优化 绿信比优化以各路口为对象,以各方向饱和度均衡为目标。绿信比合理性以相位饱和度均方差来表征,相位饱和度均方差越小,绿信比越合理。绿信比优化步骤为 Step1计算相位饱和度均方差,其计算式为 (9) (10) 式中:σ为相位饱和度均方差;μ为相位饱和度均值。 Step2判断相位饱和度均方差是否满足预设条件。若σ≤σmin,则绿信比符合要求,不进行优化,输出结果;若σ≥σmax,则绿信比不符合要求,进入step 3。其中,σmin和σmax为相位最佳饱和度均方差临界值。 Step3绿信比调整。为保证绿信比分配的精准性,采取小步距迭代优化的方式调整绿信比,将饱和度最低的相位绿信比减少Δλ,饱和度最高的相位绿信比增加Δλ,其中Δλ为绿信比调整步长。 Step4根据最大、最小绿约束对优化后的绿信比进行校验,微调。 Step5返回Step 1,进入下一次循环。 3.2.3 相位差优化 相位差优化以协调路径为对象,以带宽最优为目标。相位差的合理性以实时协调策略下的带宽来表征,带宽越大,协调效果越好;带宽越小,协调效果越差。笔者采用遍历搜索的方法优化相位差,即遍历所有相位差tp∈[0,T)下的带宽,从中根据协调策略选择最优带宽对应的相位差。以某相邻路口为例,相位差优化流程为 Step1初始化相位差tp=0。 Step2判断协调策略类型,计算协调相位差。若为绿波协调,则t’p=tp;若为红波协调,则t’p=tp+tg。其中:tp为相邻路口间绿灯相位差,s;t’p为相邻路口间协调相位差,s;tg为下游路口道路方向的绿灯时间,s。 Step3计算带宽w,若为绿波协调,则计算绿波带宽;若为红波协调,则计算红波带宽。将带宽加入带宽集合W。 Step4tp=tp+1。 Step5判断tp的大小,若tp小于T,则返回Step 2,继续迭代;否则,表示所有的相位差情况已经遍历完成,进入Step 6。 Step6相位差筛选。取集合W中最大带宽对应的相位差作为最终结果输出。 为验证算法的有效性与可行性,将其集成于中控Intellific OS信号控制系统中,并在某市的主干道(金柯桥大道、群贤路)进行现场应用验证。优化前,主干道工作日全天小时流量分布如表3所示,可以看出金柯桥大道和群贤路全天交通流量波动较大且不规律。主干道工作日全天行程时间如表4所示,可以看出高峰时段通行效率不高,现有固定时段和策略下的控制已无法满足现场多变交通流的需求,亟需全天候的动态协调信号控制来适应交通流的变化。 表3 主干道全天交通流量 表4 主干道全天行程时间 根据多源数据融合结果实时分析各道路交通态势,生成与交通态势相适应的协调策略,确保道路无拥堵且车流快速、高效率通行,各路段优化结果如表5~7所示。 表5 金柯桥大道协调策略 表6 群贤路东段协调策略 表7 群贤路西段协调策略 为验证所述算法在现场应用中的有效性,用区域宏观指标和干线微观指标两个维度的评价指标进行验证,既能反映信号控制算法对整个区域交通状况的影响,也能反映干线协调效果。以金柯桥和群贤路两条主干道为评价对象,实时统计分析工作日交通拥堵指数、行程速度、停车率、平均延误和行程时间等5项指标。其中,交通拥堵指数、停车率、平均延误和行程时间越低越好,行程速度越高越好。区域交通宏观指标对比如表8所示,应用算法后全天平均交通拥堵指数下降30%,早、晚高峰平均行程速度分别增加7.3%和15.9%,区域交通运行效率得到有效提升。主要路段信号控制微观指标对比如表9~12所示,在应用该算法后,金柯桥大道和群贤路两个方向的停车率、延误时间和行程时间在不同时段内均有所下降。统计数据表明:笔者提出的算法能有效地响应交通需求的动态变化,现场表现较好,具有一定的应用推广价值。 表8 区域交通宏观指标对比 表9 金柯桥大道(北向南)信号控制微观指标对比 表10 金柯桥大道(南向北)信号控制微观指标对比 表11 群贤路(东向西)信号控制微观指标对比 表12 群贤路(西向东)信号控制微观指标对比 利用多源融合数据,提出一种新的区域动态协调控制算法,实现了交通参数信息的有效提取、交通态势的识别和预测,用于指导交通信号控制的宏观战略决策与微观战术决策。该算法在战略层和战术层上都体现了动态自适应控制思想,前者基于交通态势实时调整信号控制的协调策略;后者以关键路口饱和度最匹配为目标实现周期优化,以交通负荷均衡为目标实现绿信比优化,以带宽最优为目标实现相位差优化。现场应用效果表明:该算法能够有效地响应实时变化的交通需求,从整体上提高区域交通控制水平和道路通行效率。3 区域动态协调信号控制算法
3.1 宏观动态协调战略决策
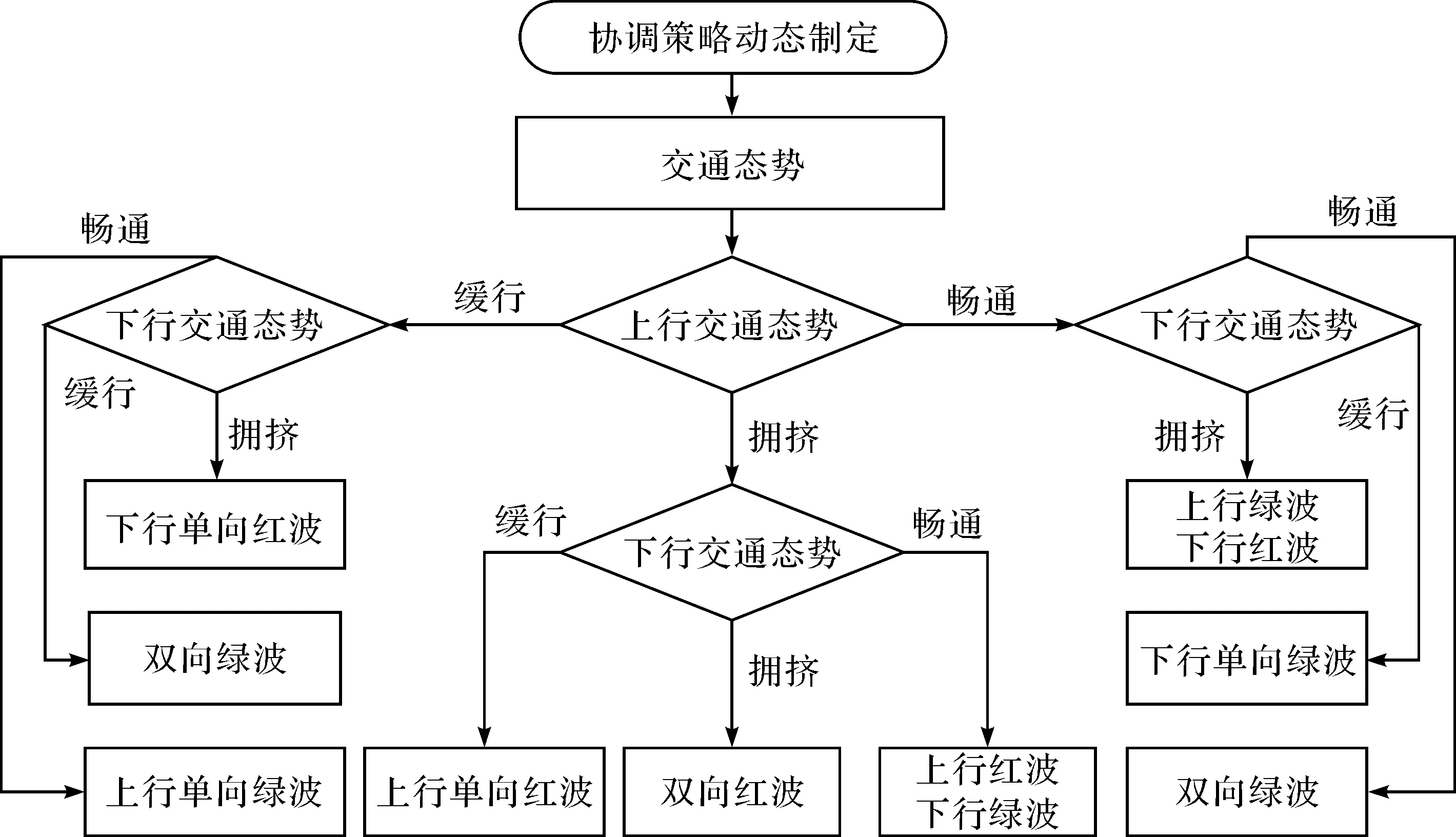
3.2 微观信号控制战术决策
4 案例分析
4.1 应用场景
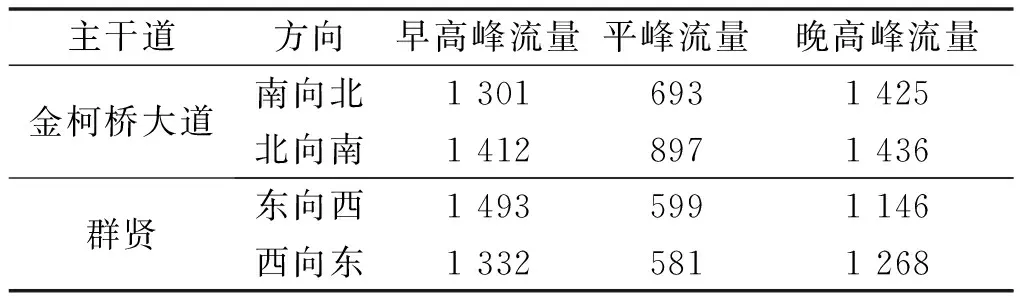
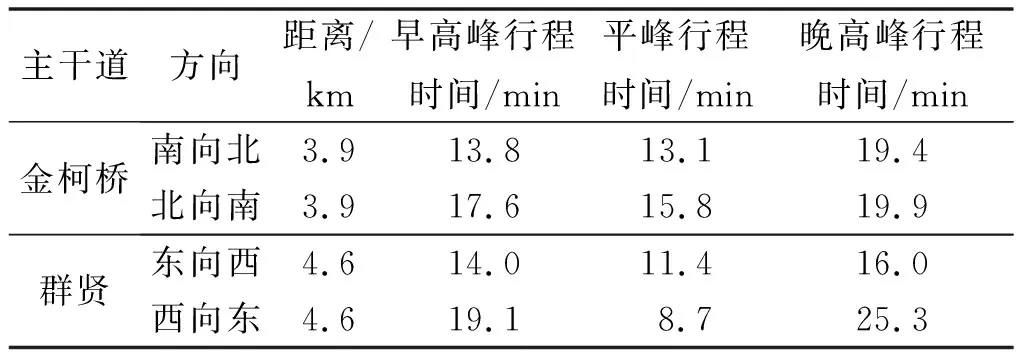
4.2 动态协调决策



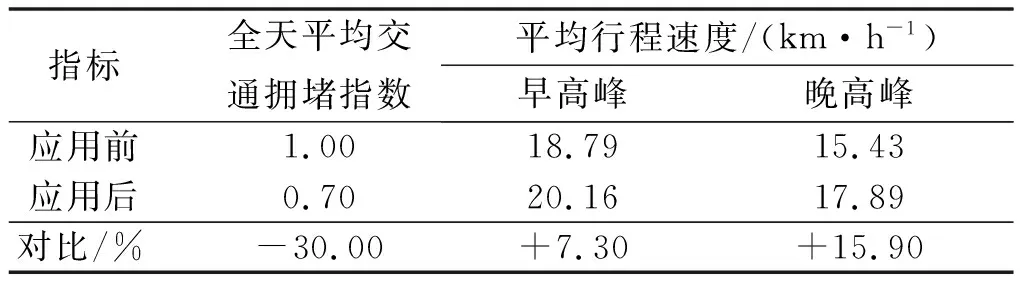
4.3 应用效果




5 结 论

