纸塑复合袋磁力压紧纠偏装置设计及优化

严国平，周俊宏，钟 飞，李 哲，周宏娣，彭震奥

（湖北工业大学机械工程学院，湖北 武汉 430068）

在缝纫工位缝合纸塑复合袋时，一般要求纸塑复合袋的中心线与整个生产线的中心重合。但是，纸塑复合袋的材料为软质柔性材料，在生产、传输过程中不易控制，尤其是当纠偏装置的前序工位已使其产生位置偏差时，其在传输过程中更易产生偏移和局部褶皱，从而影响成品质量。目前，国内外的压紧纠偏装置一般采用常规的弹簧压紧、滚筒压紧或气动压板压紧工艺。

国内外学者针对柔性体压紧纠偏装置及其优化方法做了大量研究。例如：Young等［1-2］对存在波动的薄膜进行了动力学分析，并讨论了影响薄膜动态特性的移动腹板的横、纵向运动及其张力控制方法；张前［3］以DR1075型框架偏摆式纠偏装置为研究对象，建立了薄膜应力与芯片剪应力之间的关系式，得到了薄膜张力与应力之间的关系，并通过实验对薄膜的进给速度、入口跨距及张力对纠偏效果的影响进行了验证；潘春荣等［4］设计了一种以摩擦力为驱动力的羽毛轻柔物体自动压紧装置，并分析了其压紧机理；Tsai等［5］设计了一种框架偏摆式纠偏装置，并利用MATLAB/Simulink模块对其一阶动力学模型进行了仿真分析；Ho 等［6］针对薄膜纠偏装置编写了一个动力学求解程序并完成了相应的仿真分析；Hiromu［7］对薄膜输送系统的气膜厚度进行了分析并开展了相应的验证实验；Hyeunhun 等［8］以RFID（radio frequency identification，射频识别）天线加工设备中的天线热吹模块为对象，对其远支点纠偏装置进行了仿真分析和实验研究；Shin等［9］分析了张力对薄膜横向运动及其纠偏效果的影响；Benson［10］提出了一种新的薄膜横向偏移模型；Seshadri等［11］建立了不考虑剪切变形的双辊二阶动力学模型，但该模型只适用于剪切挠度较小的情况；Beisel等［12］建立了薄膜纠偏过程中的屈曲模型，并提出了一种薄膜不稳定性的确定方法；辛键群等［13］设计了一种利用均匀排列的永磁体实现磁性压紧的皮带输送装置，但未对纸塑复合袋纠偏过程中的受力情况与起皱现象进行深入研究。

针对传统压紧纠偏方法较难解决纸塑复合袋在传输过程中易起褶皱及跑偏的问题，笔者设计了一种纸塑复合袋磁力压紧纠偏装置。首先，建立纸塑复合袋传输过程中的动态磁力压紧纠偏数学模型，并运用有限元方法进行动态仿真。然后，采用结合BP（back propagation，反向传播）神经网络和GA（genetic algorithm，遗传算法）的混合算法（下文简称为BP-GA算法）对多因素影响下的纸塑复合袋磁力压紧纠偏装置的工艺参数进行优化；最后，通过纠偏实验对所构建的动态磁力压紧纠偏理论模型进行验证，旨在为纸塑复合袋动态磁力压紧纠偏参数的优化提供一定的参考。

1 磁力压紧纠偏装置结构设计及分析

基于动态磁力和差速纠偏设计原理，对纸塑复合袋磁力压紧纠偏装置进行设计，其结构如图1所示。其中：2台电机分别驱动左、右两侧的皮带组件单独运动；每侧皮带组件均由上、下2层皮带组成，上层为磁压紧皮带，下层为普通传送带，纸塑复合袋位于上、下2层皮带之间；电磁铁均匀布置在两侧的普通传送带下方，通电后电磁铁产生磁力，使得磁压紧皮带产生向下的压紧力，从而达到均匀压紧纸塑复合袋的目的。为满足纸塑复合袋动态磁力压紧纠偏的要求，结合两侧皮带组件的差速运动，通过控制电磁铁的间距、线圈电流及其与磁压紧皮带的间距来精确控制向下的压紧力，从而实现动态磁力压紧与均匀传输。

当磁力压紧纠偏装置进行差速纠偏传输时，该装置对纸塑复合袋施加压紧力。由于左、右两侧皮带组件的运动方向相反，纸塑复合袋左、右两侧所受摩擦力的方向相反。在由摩擦力产生的力矩的作用下，纸塑复合袋绕自身中点O旋转，从而完成纠偏。图2所示为磁力压紧纠偏过程中纸塑复合袋的受力分析。图中：v1、v2分别为左、右两侧皮带组件的速度；f1、f2分别为左、右两侧皮带组件对纸塑复合袋的摩擦力；ω为纸塑复合袋的加速度；φ为纸塑复合袋与垂直于皮带组件方向的夹角；Lm为左、右两侧皮带组件的间距。

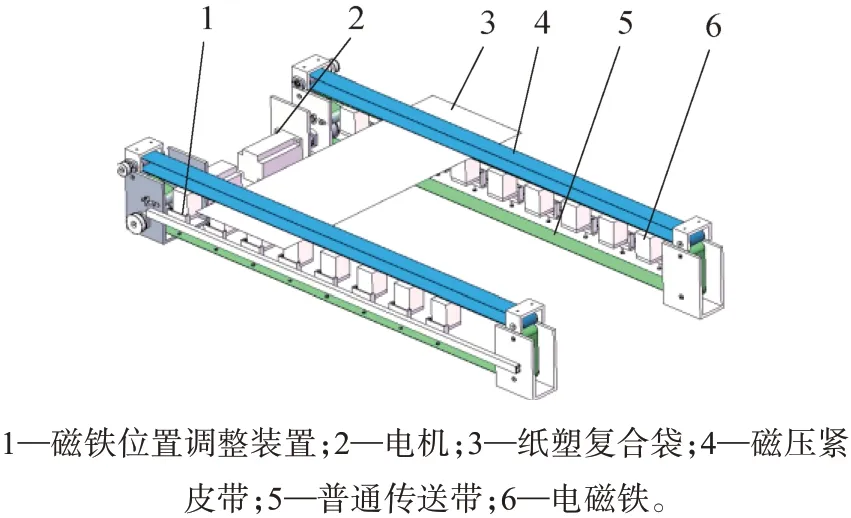
图1 纸塑复合袋磁力压紧纠偏装置结构Fig.1 Structure of magnetic compression correction device for paper-plastic composite bag

图2 磁力压紧纠偏过程中纸塑复合袋的受力分析Fig.2 Force analysis of paper-plastic composite bag during magnetic compression correction process

由图2可知，在磁力压紧纠偏过程中，纸塑复合袋所受的力矩M及其转动惯量J分别为：

式中：ρ为纸塑复合袋的密度；m为纸塑复合袋的质量；r为纸塑复合袋微元的转动半径；dm0为纸塑复合袋微元的质量；c、d、h分别为纸塑复合袋的长度、宽度和高度。

则纸塑复合袋的旋转角加速度α为：

由式（3）中可知，摩擦力越大，纸塑复合袋的旋转角加速度越大，则纠偏所需的时间越短；左、右两侧皮带组件的间距越大，纸塑复合袋的旋转角加速度也越大，则纠偏所需的时间也越短。但在实际纠偏过程中，由于上、下2层皮带与纸塑复合袋接触不均匀导致纸塑复合袋左、右两侧所受摩擦力存在差异，以及左、右两侧皮带组件存在一定程度的速度差和纸塑复合袋为柔性体等因素，使得纸塑复合袋产生局部变形。若纸塑复合袋的局部变形过大，则容易产生褶皱。本文将采用有限元方法对纸塑复合袋磁力压紧纠偏装置的动态纠偏过程进行仿真分析。

2 磁力压紧纠偏装置动态纠偏过程仿真分析

为减少仿真运算量，仅对纸塑复合袋磁力压紧纠偏装置中存在相互作用的皮带组件和纸塑复合袋进行简化建模。在仿真模型中，托板材料设置为铝合金；为准确模拟均匀分布的压紧力，在仿真模型中设置多个磁力作用板，其大小和数量与电磁铁相同。构建的纸塑复合袋磁力压紧纠偏装置仿真模型如图3所示，模型中涉及的材料参数如表1所示。设纸塑复合袋纠偏前的最大偏移角度为10°。

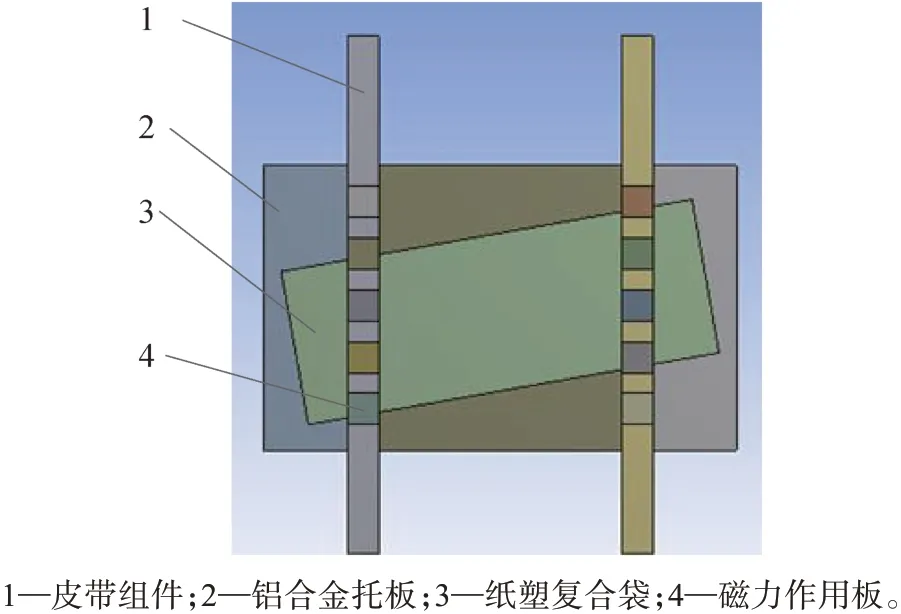
图3 简化的纸塑复合袋磁力压紧纠偏装置仿真模型Fig.3 Simplified simulation model of magnetic compression correction device for paper-plastic composite bag

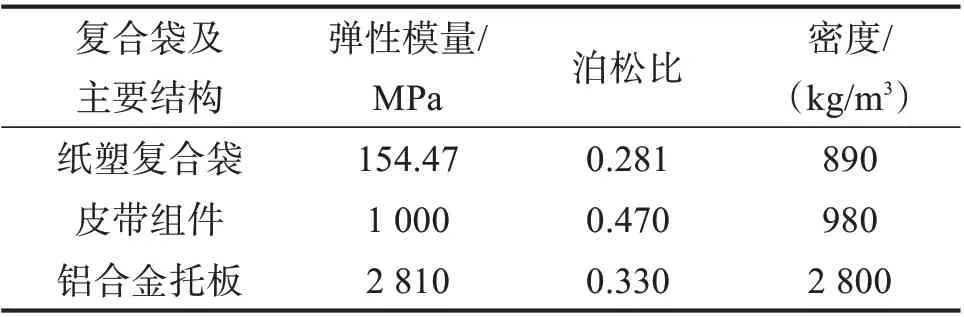
表1 纸塑复合袋及其磁力压紧纠偏装置主要结构的材料参数Table 1 Material parameters of paper-plastic composite bag and main structures in magnetic compression correction device

纸塑复合袋磁力压紧纠偏装置仿真模型的边界条件设置如下：1）通过磁力作用板对磁压紧皮带表面施加均匀的磁力；2）左、右两侧普通传送带处于完全张紧状态且只沿Y方向作速度大小相同、方向相反的运动，约束其X、Z 方向的位移，并设其速度大小为0.1 m/s；3）约束磁压紧皮带X方向的位移，并设其速度大小为0.1 m/s；4）对托板施加固定约束；5）定义普通传送带与托板上表面、普通传送带与纸塑复合袋下表面以及纸塑复合袋上表面与磁压紧皮带下表面的摩擦关系，设皮带组件与纸塑复合袋之间的动摩擦系数为0.20，普通传送带与托板之间的动摩擦系数为0.02。设仿真时间为0.06 s，对纸塑复合袋磁力压紧纠偏装置的动态纠偏过程进行仿真分析，结果如图4所示。

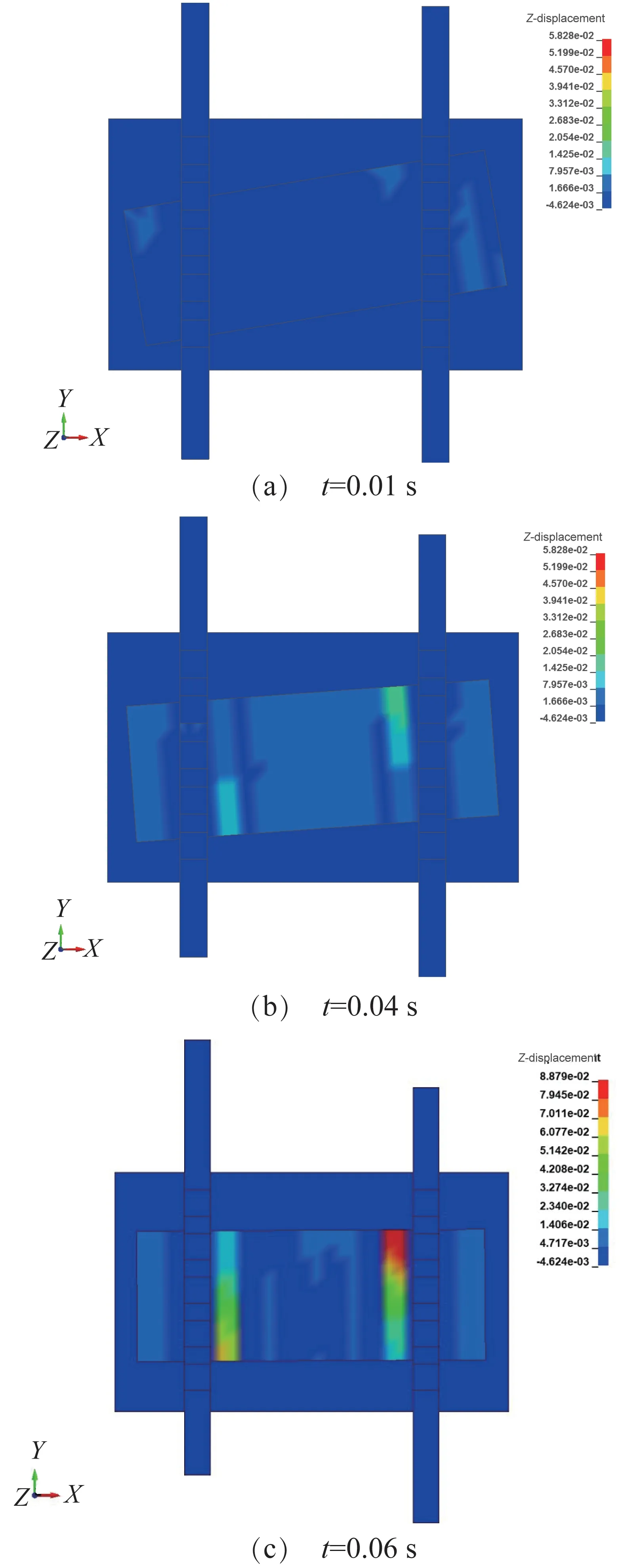
图4 纠偏过程中纸塑复合袋的Z向变形云图Fig.4 Z-directional deformation nephogram of paperplastic composite bag during correction process

从图4中可以看出，在纠偏开始前，纸塑复合袋为展平状态；随着纠偏的进行，在压紧力及摩擦力的作用下，纸塑复合袋的Z向（垂直于纸面）变形越来越大，且主要集中于右侧皮带组件内侧前部和左侧皮带组件内侧后部。在纠偏过程中，纸塑复合袋绕自身中心O旋转，直至到达水平方位（纠正状态），即完成纠偏。

如图5所示，在整个纠偏过程中（t=0.01 s时装置达到稳定状态），在两侧方向相反的摩擦力的作用下，纸塑复合袋产生的褶皱（Z向变形量）呈非线性增大；当纸塑复合袋达到纠正状态时，其褶皱达到最大。

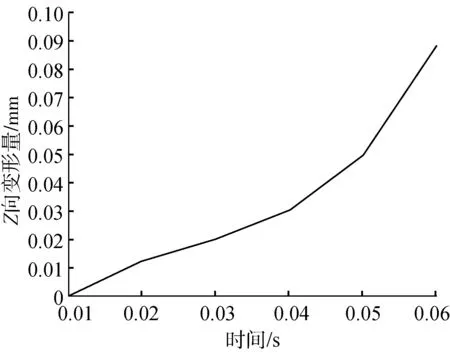
图5 纠偏过程中纸塑复合袋的Z向变形量变化曲线Fig.5 Z-directional deformation curve of paper-plastic composite bag during correction process

3 基于BP-GA的磁力压紧纠偏装置工艺参数优化

在纸塑复合袋磁力压紧纠偏过程中，存在较多耦合因素，且各因素呈强耦合状态，故采用BP-GA算法对磁力压紧纠偏装置的工艺参数进行全局寻优。近年来，国内外学者针对BP-GA算法做了很多研究，其已较为成熟。例如：Lu等［14］提出了一种将GA应用于结构优化的改进策略；Nicholas等［15］为提高风力涡轮机结构的屈曲强度，用人工神经网络代替有限元分析，降低了计算成本；Gong 等［16］利用BP-GA 算法对钢铸件送料系统进行优化，防止其产生收缩孔和孔隙；刘青春等［17］在正交试验的基础上，利用BP-GA算法得到了最优的展成法球面磨削参数组合；胡海涛［18］提出了一种将BP神经网络与GA相结合的迭代优化方法。

利用BP-GA 算法进行全局寻优的基本思路为［19］：首先，通过仿真分析得到样本数据；然后，利用样本数据对BP神经网络进行训练，得到较为准确的BP 神经网络预测模型；最后，利用GA 进行全局寻优。

上文理论分析和仿真分析结果表明，在纠偏过程中，纸塑复合袋的变形越大，其所需的纠偏时间越短。根据纸塑复合袋在实际纠偏过程中的Z向最大变形量小于0.5 mm的工艺要求，选择纸塑复合袋的Z向最大变形量最接近0.5 mm作为优化目标。建立纸塑复合袋磁力压紧纠偏装置工艺参数优化模型，为：

式中：Smax为纸塑复合袋的Z向最大变形量；F1、F2分别为电磁铁磁力F的最小值和最大值；b1、b2分别为两侧皮带组件的间距b值的最小值和最大值；a1、a2分别为皮带组件与纸塑复合袋之间动摩擦系数μ1的最小值和最大值。

令F=5～7 N，b=465～485 mm，μ1=0.10～0.30，开展三因素五水平正交试验，共获得25组纸塑复合袋磁力压紧纠偏装置工艺参数。对不同工艺参数下纸塑复合袋磁力压紧纠偏装置的动态纠偏过程进行仿真分析，获得25 个纸塑复合袋Z向最大变形量的仿真值。同时，采用BP 神经网络进行预测，得到25个纸塑复合袋Z向最大变形量的预测值，结果如表2所示。

从表2 中可以看出，BP 神经网络预测结果与有限元仿真结果基本吻合，两者的最大相对误差为2.952 5%，这表明建立的BP神经网络预测模型较为准确。在全局范围内，可用BP神经网络的预测值来定义目标函数，并采用GA 对目标函数进行全局寻优。利用GA 进行寻优时，设种群中的个体数量为50，最大遗传代数为200，变量二进制位数为30，代沟为0.9，交叉概率为0.7。GA 寻优过程中目标函数值的变化情况及遗传代数为200时各种群个体对应的目标函数值分别如图6和图7所示。

由图6可知，当遗传代数达到60后，目标函数值几乎不变，说明GA寻优迭代至第60代时即可达到收敛，此时对应的工艺参数为纸塑复合袋磁力压紧纠偏装置的最优工艺参数。由图7 可知，当遗传代数为200时，仅1个个体偏离目标值较远，其余均在可接受的范围内，这说明GA的寻优精度较高。基于寻优得到的最优工艺参数，对纸塑复合袋磁力压紧纠偏装置的动态纠偏过程进行仿真分析。优化前后纸塑复合袋磁力压紧纠偏装置的工艺参数及性能对比如表3所示。

表2 不同工艺参数下纸塑复合袋Z向最大变形量对比Table 2 Comparison of maximum Z-directional deformation of paper-plastic composite bag under different process parameters

图6 GA寻优过程中目标函数值的变化情况Fig.6 The change of objective function value during GA optimization process

从表3 中可以看出，在利用BP-GA 算法寻优得到的最优工艺参数下，纸塑复合袋在磁力压紧纠偏过程中的Z向最大变形量比优化前更接近0.5 mm，表明优化结果较为理想。

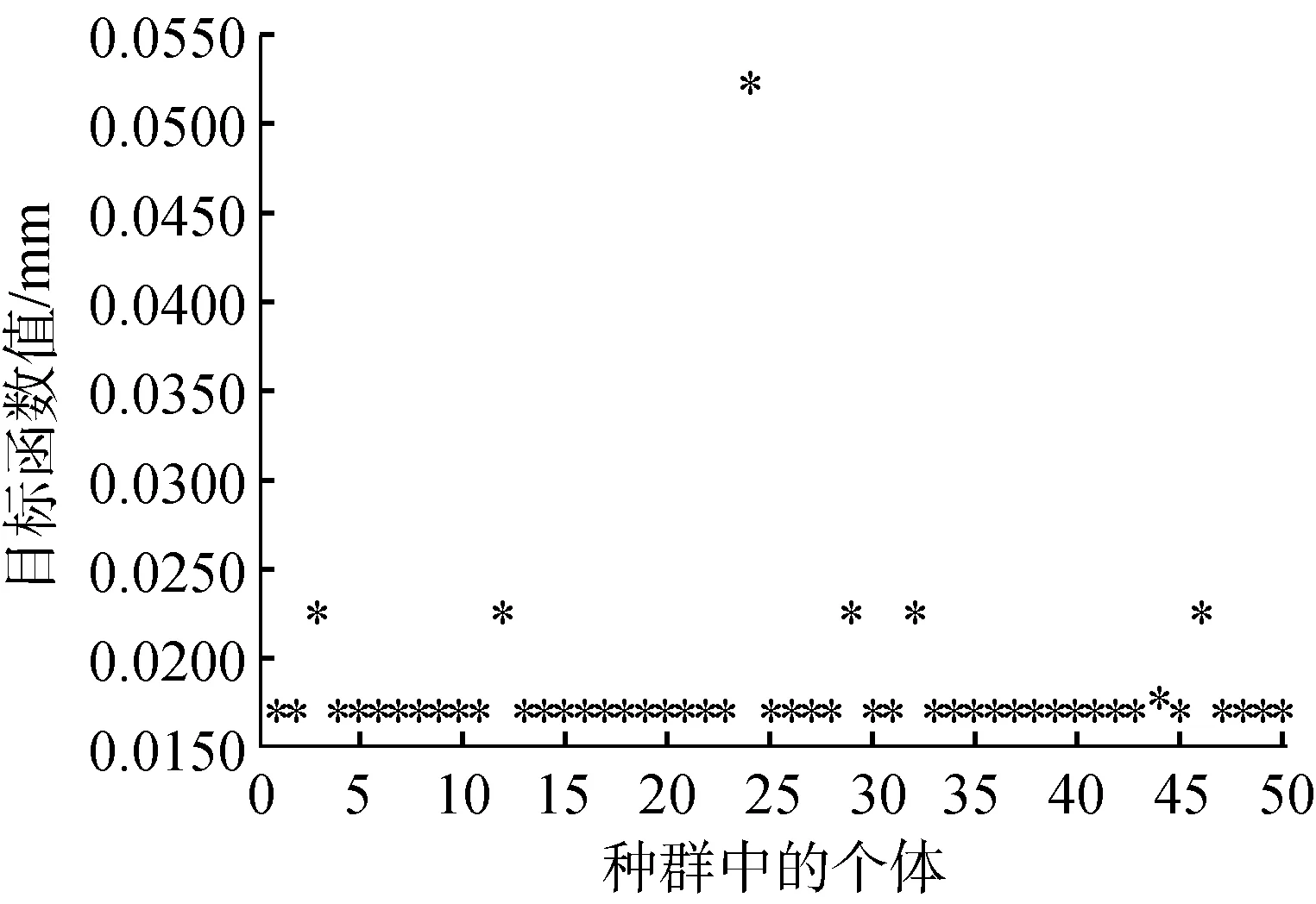
图7 遗传代数为200时各种群个体对应的目标函数值Fig.7 Objective function value corresponding to each group individual with genetic algebra of 200

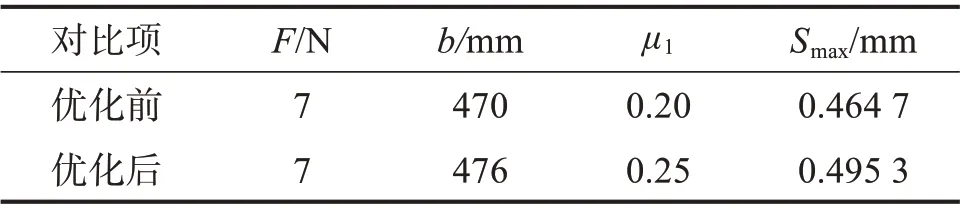
表3 优化前后纸塑复合袋磁力压紧纠偏装置的工艺参数及性能对比Table 3 Comparison of process parameters and performance of magnetic compression correction device for paper-plastic composite bag before and after optimization

4 纸塑复合袋纠偏实验

纸塑复合袋磁力压紧纠偏装置样机如图8所示。基于该装置，对尺寸为800 mm×300 mm×0.5 mm 的纸塑复合袋进行纠偏与传输。先调节左、右两侧电磁铁的间距，以保证纸塑复合袋在纠偏过程中所覆盖的电磁铁的面积一致，从而确保纸塑复合袋受到的压紧力与其运动位置无关。当纸塑复合袋完全进入磁力压紧纠偏装置时，通过视觉识别检测纸塑复合袋的偏移量和偏移方向；当PLC（programmable logic controller，可编程控制器）接收到纸塑复合袋当前的状态信息后，控制左、右2 个电机的转速和转向，以调节左、右两侧皮带组件的间距和通入电磁铁的电流大小，从而调节纸塑复合袋所受的力矩。观察纸塑复合袋在纠偏过程中的褶皱情况并记录纠偏时间。对于该磁力压紧纠偏装置，纸塑复合袋褶皱的评定标准为其Z向最大变形量不超过0.5 mm。在纠偏过程中，采用精度为0.01 mm 的游标卡尺来测量纸塑复合袋的Z向变形量。

在纸塑复合袋的纠偏与传输过程中，通过改变通入电磁铁的电流，得到纸塑复合袋磁力压紧纠偏装置的最优工艺参数为：电磁铁磁力为7 N，左、右两侧皮带组件的间距为476 mm，皮带组件与纸塑复合袋之间的动摩擦系数为0.25，这与基于BP-GA 算法的寻优结果一致。

图8 纸塑复合袋磁力压紧纠偏装置样机Fig.8 Prototype of magnetic compression correction device for paper-plastic composite bag

5 结 论

通过对纸塑复合袋磁力压紧纠偏装置进行动态仿真与工艺参数优化，得到以下结论。

1）所设计的磁力压紧纠偏装置能较好地满足纸塑复合袋的纠偏工艺要求。在纠偏过程中，摩擦力越大及皮带组件的间距越大，纸塑复合袋的旋转角加速度越大，则纠偏所需时间越短。因此，须根据纸塑复合袋的纠偏要求，对所设计装置的工艺参数进行优化。

2）仿真结果表明：在纠偏过程中，纸塑复合袋产生的褶皱（Z向变形量）呈非线性增大。当纸塑复合袋处于纠正状态时，其Z向变形量达到最大，变形主要集中于右侧皮带组件内侧前部与左侧皮带组件内侧后部。

3）利用BP-GA 算法寻优得到的最优工艺参数为：电磁铁磁力为7 N，左、右两侧皮带组件的间距为476 mm，皮带组件与纸塑复合袋之间的动摩擦系数为0.25。在最优工艺参数下，纸塑复合袋在纠偏过程中的Z向最大形变量不超过0.5 mm，且满足纠偏时间最短的要求。

4）通过纸塑复合袋纠偏实验获得的磁力压紧纠偏装置的最优工艺参数与利用BP-GA算法寻优得到的结果一致，表明BP-GA 算法可以较好地解决纸塑复合袋纠偏装置工艺参数优化模型中设计变量与设计目标之间的强耦合问题，具有较高精度与可信度，可为同类问题的解决提供参考。