面向广域海洋覆盖的密集低轨卫星星座

王鹏飞，邸博雅，唐 斌，王成才，宋令阳*，陆 军

(1.北京大学 信息科学技术学院，北京100871；2.中国电子科学研究院，北京 100041)

0 引言

海洋范围辽阔、资源丰富、环境复杂，是未来网络信息技术发展和竞争的重要方向[1]。然而，不同于陆地网络信息系统，受限于海洋环境，海洋区域难以架设高密度的地面基站[2]。为了构建海洋通信网络，需要使用广覆盖、高可靠的网络信息技术。超高密度低地球轨道(LEO)卫星通信可以实现广域海洋的全面覆盖，并利用视距链路提供可靠的大容量数据传输服务[3-5]。传统工作主要研究了同高度LEO卫星星座设计[6]，讨论了诸如卫星数量[7]、覆盖率[8-9]以及传输延时[10]等优化问题，但海陆混合的异构地面-卫星通信网络仍面临多种挑战：第一，海洋和陆地的差异化环境和通信需求需要更加精细灵活的卫星部署方案；第二，低轨卫星的高移动性导致静态卫星拓扑假设并不合理，应该结合纬度考虑动态卫星星座设计；第三，流量会影响链路活跃性和干扰，星座设计应该综合考虑覆盖率、回程链路容量需求和网络数据流量。为了应对以上挑战，本文利用了随机几何和概率论、排队论理论推导分析了流量影响下的密集低轨卫星网络容量，基于极轨道卫星部署，利用动态规划和优化论方法设计了面向广域海洋覆盖的密集LEO卫星星座部署方案，以实现用最少的卫星数量同时满足陆地与广域海洋覆盖区域内所有用户的通信需求。

1 系统模型

本节面向广域海洋覆盖的密集LEO卫星-地面通信网络进行研究和建模，首先给出一种可以同时服务海洋和陆地用户的密集LEO卫星部署架构，之后利用排队论给出海洋和陆地地面站的数据流量到达模型，并就卫星轨道和覆盖区域进行建模，最后，将给出密集卫星框架下的海陆回程传输模型。

1.1 密集低轨卫星部署架构

如图1所示，密集卫星部署架构可以同时服务海洋和陆地用户，网络包括两部分：地面站(海洋和陆地)和LEO卫星群。数据由海洋或陆地地面站在Ka频段经由回程链路上传到任意轨道高度的卫星，并通过相应卫星接入核心网络。海洋和陆地地面站的位置分布均服从泊松点过程，而分布密度有着显著的差异，假设海洋地面站(比如轮船)的分布密度为λ1，陆地地面站的分布密度为λ2。

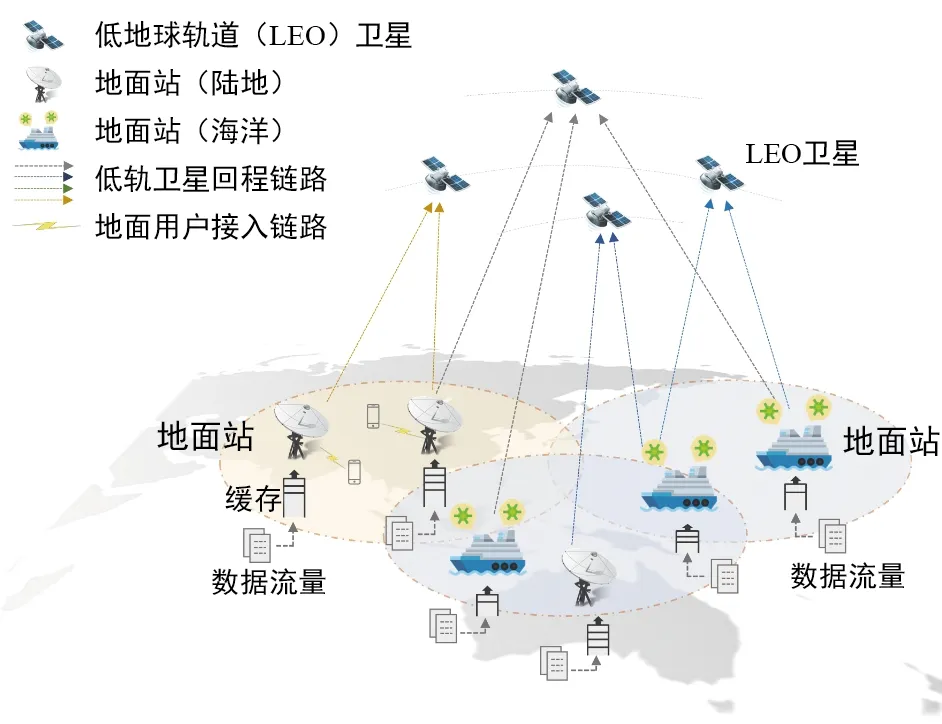
图1 海陆密集卫星部署架构Fig.1 Ultra-dense LEO satellite-terrestrial network structure

1.2 数据流量模型

假设数据包到达海洋或陆地地面站的过程服从到达速率为ξ的伯努利过程，数据包传到地面站后会进入该地面站的缓存中，并按照先来先服务(First-Come Firs-Serve,FCFS)顺序参与传输。根据排队论模型，排队传输的过程可以建模为一个到达速率为ξ的Geo/Geo/1队列。设地面站q的数据传输速率为Cq，即该节点处的数据离开率。根据律特法则，可以得到地面站q的平均活跃概率(参与数据传输的概率)为：

(1)

1.3 卫星轨道和覆盖模型

如图2所示，考虑圆形低轨卫星轨道模型[1]，卫星的位置坐标由经典的六坐标退化为以下3个参量，分别为轨道倾角i、升交点赤经Ω和卫星角距ω。根据地球半径R、卫星轨道高度h和前述这些参量，可以建模卫星位置的笛卡尔坐标：

(2)

图2 卫星轨道重要参数Fig.2 Main parameters of the satellite orbit

每个地面站都存在一个最小仰角θmin，当上空的卫星位于仰角内时，可以建立与卫星的回程链路。如图3所示。

图3 卫星覆盖区域示意Fig.3 Coverage region illustration of the LEO satellite

卫星的覆盖范围直接由地面站最小仰角θmin和卫星轨道高度h决定。将地球视作一个正球体，并用下标l代表卫星m所处的轨道高度序号(l=1表示卫星轨道高度为h1，l=2表示星轨道高度为h2)，那么卫星覆盖区域为一个球冠，对应的角半径为：

(3)

覆盖面积为：

(4)

1.4 数据传输模型

下面讨论地面站q在时隙t内的回程链路，为了表示的简便，在后述中省略下标t。针对地面站q与hl高度卫星m的链路，传输SINR表示为：

(5)

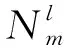
(6)

而地面站q的总回程容量可以表示为：

(7)

2 平均回程容量分析

在本节中，利用随机几何和概率论知识，对分布密度为λ的地面站平均回程容量进行分析和推导。首先对回程链路的干扰进行分析，再给出平均回程容量的表示。

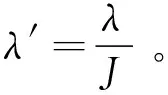
(8)

利用坎贝尔定理可以推导平均网络干扰为：

(9)

其中，Φ表示地面站构成的集合，a表示TST的平均活跃概率，a=表示干扰区域内的TSTq' 与hl高度卫星m的距离构成的集合，干扰包括同高度回程干扰和不同高度回程干扰两部分，表示为：

(10)

(11)

(12)

(13)

图4 同轨道高度卫星干扰示意图Fig.4 Illustration of co-layer interfering range

因此，利用积分变换可以计算得到：

(14)

(15)

进一步利用积分变量替换推导可得：

μl=

(16)

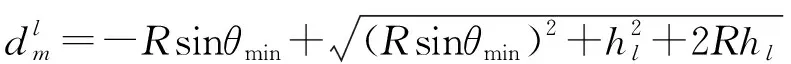
(17)

其中，2F1(·)为广义超几何函数，而

(18)

根据地面站泊松点分布特性，每个卫星覆盖范围内的地面站数量服从泊松分布，因此在密度为λ的区域，hl高度卫星的每条星地链路的平均传输速率可以表示为：

Cl(kl)=

(Ei(λSl)-ln(λSl)-γ)e-λSl·B·μl，

(19)

(20)

3 最少卫星覆盖问题

首先要确定为了达到传输需求，海洋和陆地地面站需要最少连接的不同轨道高度的低轨卫星数量，可以表示为：

(21)

该问题是一个非线性多元整数优化问题，难以直接推导出最优解。下面以两种卫星轨道高度(即L=2)为例，求解最少卫星覆盖问题，设计密集低轨卫星星座部署方案，并评估网络性能。

根据海洋和陆地的分布密度和传输速率需求，设计了一种动态规划算法进行求解，用Num(k1,k2)表示在地面站连接k1个h1高度LEO卫星和k2个h2高度LEO卫星时所需的总卫星数量，根据式(11)可知Num(k1,k2)=K1(k1)+K2(k2)，根据动态规划算法，不同结果间的递推关系可以表示为：

(22)

4 海陆密集低轨卫星星座部署方案

广域海洋覆盖内，地面站依托于轮船而在海域内不断移动，因此密集卫星部署需要考虑整个海域的全域传输需求，而不能只针对某些固定位置提供符合要求的数据回程服务。因此对于全球范围内，任意位置地面站所连接的卫星数量都要满足上一章中优化得到的连接要求。

4.1 全球覆盖初始密集低轨卫星星座部署

采用经典的极点低地球轨道卫星星座来初始化星座部署[11]。首先考虑单颗卫星全球覆盖的情况，假设每个轨道高度部署的卫星都有N0条卫星轨道，hl高度上每条卫星轨道上的卫星数量均为Ml，那么满足以下关系：

(N0-1)φ+(N0+1)Δ=π,

(23)

其中,φ表示卫星覆盖范围的角半径，由式(3)给出，而Δ=cos-1[cosφ/cos(π/Ml)]。该公式给出了卫星轨道数量N0、每条轨道上的卫星数量Ml、轨道高度hl、地面站最小仰角θmin之间的闭式关系。

。

4.2 海陆密集LEO卫星星座部署方案

在实际卫星部署中，需要考虑卫星按轨道的旋转移动。在极点轨道的部署方案中，在高纬度区域内，由于卫星轨道的汇聚，卫星的密度会明显增加，有很大概率提供超过所需的容量需求而出现卫星冗余。另外，因为要同时满足海洋用户和陆地用户有差异的传输容量和覆盖率需求，需要综合考虑密集LEO卫星网络的服务能力和卫星布置。

4.2.1 卫星布置的主要原则

原则一：如果卫星m的任意覆盖区域都已经满足不同轨道高度下kmin的连接需求，那么该卫星为冗余卫星，可以去除；否则，该卫星可以入选密集LEO卫星星座部署方案。

然而，对于某颗卫星覆盖区域的每个点都进行检查显然是不现实的，因此可以对卫星m与周围卫星的覆盖区域交点进行判断，如果所有交点都满足不同轨道高度下kmin的连接需求，那么可以认为该卫星是冗余的[12]。

原则二：对于不同轨道高度卫星的部署，考虑到卫星的移动性，高纬度区域和低纬度区域的部署方式不同。在低纬度按照kl,min卫星数量需求连接，在高纬度按照kl,max(kl,max≥kl,min)卫星数量需求连接。

如果在高纬度区域判定过多的冗余卫星，那么当这些卫星沿轨道运动到低纬度时，就会出现覆盖区域的显著降低，很有可能无法满足海洋和陆地地面站的覆盖率要求。因此需要在高纬度区域内参考更大的卫星连接数量要求判断卫星的冗余与否，而卫星网络kmax的选择可以利用二分法[13]实现。

4.2.2 海陆密集LEO卫星星座部署设计

1.初始化

① 按照第4节极点卫星轨道初始化卫星位置；

② 高纬度卫星连接数量准则上下界 (kmax)Lower=kmin,(kmax)Upper=kmax；

③ 高纬度卫星连接数量准则km=(kmax)Lower,kM=(kmax)Upper。

2.海陆密集LEO卫星部署优化

b.对该轨道高度所有卫星按4.2.1中原则判断并删除冗余卫星；

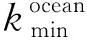
d.判断覆盖率ρ是否达标，并相应更新上下界km和kM；

e.更新最少卫星数量。

b.对该轨道高度所有卫星按4.2.1中原则判断,并删除冗余卫星；

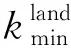
d.判断覆盖率ρ是否达标，并相应更新上下界km和kM；

e.更新最少卫星数量。

③ 比较海洋准则和陆地准则下的卫星数量，按照更多数量需求的方案部署卫星网络。

5 仿真结果

给出海陆密集LEO卫星星座部署方案在不同覆盖率要求、地面站分布密度、地面仰角和卫星轨道数量情况下需要的卫星总数量变化规律，探讨了海洋、陆地的差异化需求带来的影响。

5.1 仿真实验参数设计

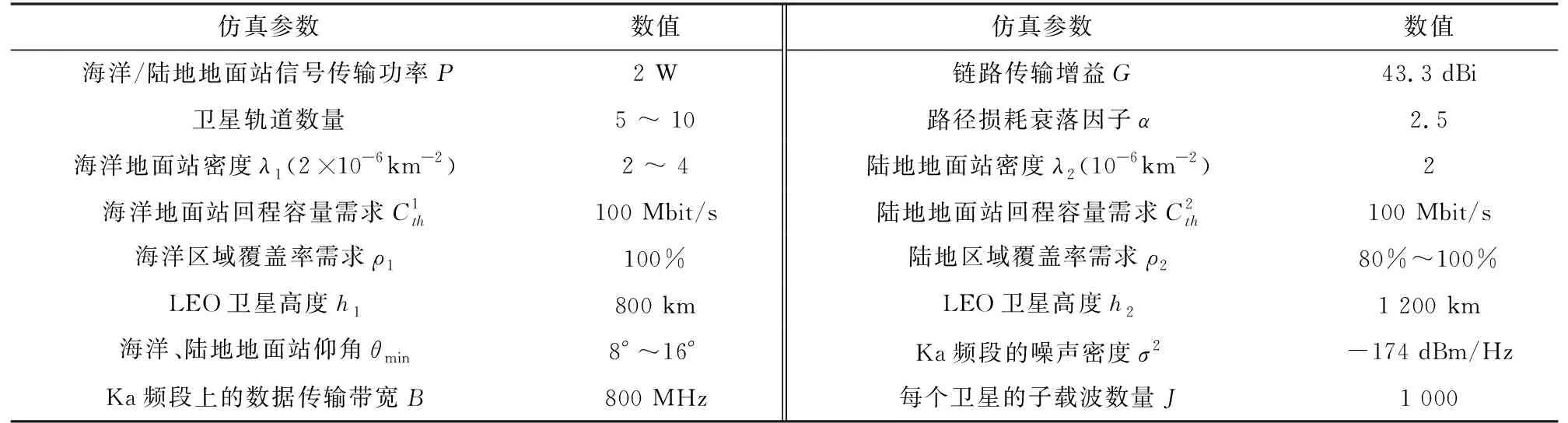
表1 主要仿真实验参数

5.2 覆盖率需求与流量大小的影响

如图5所示，在大流量情况(流量为100 Mbit/s)下，随着陆地区域覆盖率需求从80%逐渐增长到100%的过程中，所需要的卫星总数量逐渐增大，以实现更高的覆盖率。而在小流量情况(流量为50 Mbit/s)下，在陆地区域覆盖率需求不超过85%时，所需要的卫星总数保持不变，这是因为要同时满足海洋区域的100%覆盖率需求，至少需要168颗卫星，因此即使陆地区域满足传输需求并只需要更少的卫星，为了实现海陆全域覆盖，最少仍需要168颗卫星。

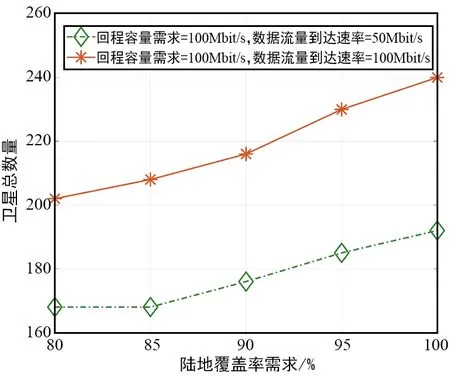
图5 卫星总数量随陆地覆盖率需求的变化(海洋100%覆盖)Fig.5 Total number of LEO satellites v.s. land coverage requirement (100% ocean coverage)

5.3 卫星网络的优势

如图6所示,在不同的陆地地面站密度下，对比了同高度LEO卫星网络和不同高度部署的LEO网络为了同时满足海洋和陆地的传输和覆盖需求所需要的卫星数量。

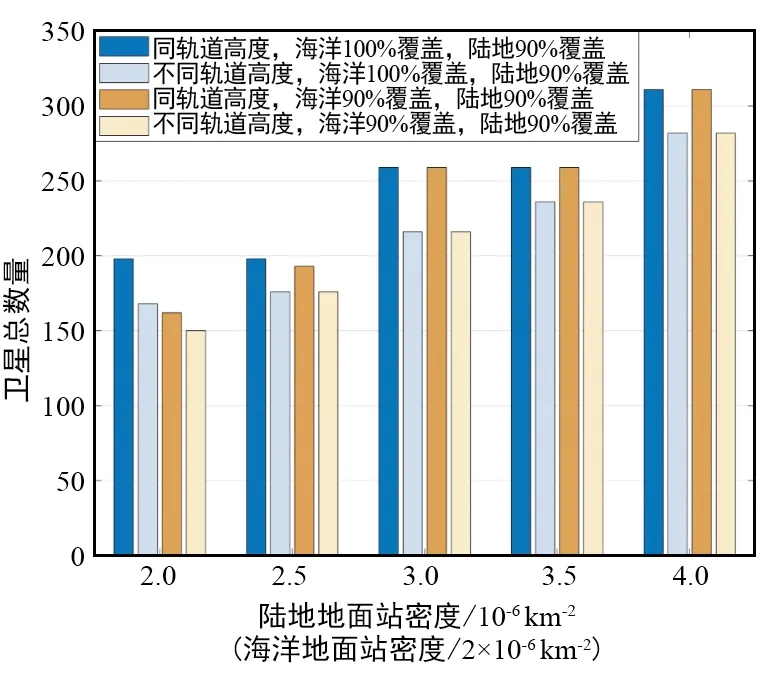
图6 同高度与不同高度部署的卫星数量对比Fig.6 Compare of satellite number in different constellation deployment schemes

随着地面站密度的增大，所需要的总卫星数量也随之增加。更大的地面站密度导致了每个地面站分配到的带宽减少、干扰增大，总的传输容量需求也随之增大，因此需要的卫星数量增多。得益于卫星网络中不同轨道高度提供的差异化的服务能力，借助高轨道高度的LEO卫星更大的覆盖区域和更细粒度的传输容量调节，卫星可以实现更加精细化的覆盖调节和更加丰富的卫星连接选择，从而有效减少了部署的卫星数量，节约了成本。

5.4 地面站最小仰角的影响

考虑在海洋地面站密度2×10-6/km2、海洋传输覆盖需求(100 Mbit/s，100%)，陆地地面站密度4×10-6/km2、陆地传输覆盖需求(100 Mbit/s，80%)的情况，图7为按照陆地准则、海洋准则和综合考虑海陆差异化需求情况下的卫星数量随地面站最小仰角的变化趋势。

图7 卫星总数量随地面站最小仰角的变化Fig.7 Total number of LEO satellites v.s. minimum elevation angle of TSTs

按照陆地准则部署卫星时，随着地面站最小仰角的增大，卫星总数量先减少后增大，最优θmin=14°。因为一方面每颗卫星的覆盖范围减小，每个轨道上的卫星部署数量增多；另一方面相邻卫星覆盖区域内的回程干扰减小，每颗卫星覆盖范围内服务用户减少，使得每个地面站的传输容量增大。综合考虑卫星覆盖区域和地面站回程容量，卫星总数量随着地面站最小仰角的增大先减少再增加。

而采用海洋准则部署卫星时，所需卫星数量随着地面站最小仰角的增大而增加，因为海洋地面站密度较小，增大地面站仰角对相邻覆盖区域的回程干扰影响较小，卫星覆盖范围减小带来的卫星数量增大起到主导作用，因此卫星数量随着地面站最小仰角增大而持续增加。

综合考虑海洋和陆地区域对传输和覆盖率的差异化需求，随着地面站最小仰角的增大，海陆LEO卫星部署总数量先减少后增大，在仰角为12°时，所需要的卫星数量最少。由此可见，海洋和陆地的差异化需求会影响最优最小仰角的取值，如果只考虑陆地需求，最优θmin=14°，如果只考虑海洋需求，最优θmin=8°，综合考虑海洋和陆地区域后，最优θmin=12°，所以地面站分布密度和覆盖率需求会影响最优地面站最小仰角的选值。

5.5 卫星轨道数量的影响

单覆盖卫星轨道数量与每条轨道上的卫星数量服从式(23)描述的闭式关系，如图8所示，采用海洋准则和陆地准则需要的卫星数量随卫星轨道数量的变化分别用蓝色和红色折线表示综合考虑了海洋和陆地的差异化需求后，所需的卫星数量用条形图表示。可以发现，随着卫星轨道数量的增大，所需要的LEO卫星总数量会先减小后增大，与式(23)得到的趋势一致，因此本文采用6条卫星轨道进行海陆密集LEO卫星部署，以最小化卫星总数量。

图8 卫星总数量随单覆盖卫星轨道数的变化Fig.8 Total number of LEO satellites v.s. number of orbits for single-coverage

6 结束语

本文就面向广域海洋覆盖的密集低轨卫星通信网络展开研究。利用随机几何和概率论、排队论理论推导分析了流量影响下的密集低轨卫星网络可以提供的地面站平均回程容量。设计了一种密集低轨卫星星座部署方案，能够用最少的卫星数量，同时满足海洋和陆地地面站的数据传输和网络覆盖需求。第一，为了应对海洋和陆地的差异化通信需求，不同高度的低轨卫星部署方案提供了更精细的覆盖调节和更灵活的传输选择，可以有效减少卫星数量，节约成本。第二，通过在高纬度和低纬度采用不同的卫星部署方案，考虑了LEO卫星移动性对覆盖率带来的影响。第三，综合考虑回程容量和数据流量对地面站活跃状态的和信道干扰大小的影响，分析了不同流量下卫星网络的回程容量，为卫星网络随流量变化的动态调整提供了可靠的理论依据，并通过仿真发现，流量越大、覆盖率需求越高，所需部署的卫星数量越多。第四，可以通过调整地面站最小仰角，实现覆盖面积和回程容量的平衡，存在最优的地面站最小仰角和卫星轨道数量，可以最小化卫星数量。