一种能够实现双层稀疏性的Group Logarithm模型

崔立鹏, 郭红霞, 沈 洁

（天津轻工职业技术学院 电子信息与自动化学院，天津 300350）

在人工智能、机器学习和数据挖掘等领域，很多分类和回归问题的解释变量空间维数很高，甚至是超高维的。然而，高维数据会导致机器学习中的过拟合现象，从而使统计模型的泛化性能变差。因此，对变量空间降维与变量选择问题成为学界研究的热点。变量选择的目的在于两个方面：一是实现精确的预测和分类；二是使模型具有更好的可解释性，降低统计模型的复杂度。所谓可解释性指的是模型的简洁度。显然，变量空间维数越低的统计模型可解释性越好。

如何实现统计模型的变量空间降维？Tibshirani[1]提出的基于L1范数罚的Lasso可有效实现变量空间的降维。Lasso使用L1范数罚的思想可以引入其他领域，例如将其引入支持向量机（support vector machine，SVM）中构成稀疏支持向量机，从而在实现分类的同时进行模型空间的降维。在Lasso刚被提出时，信息技术与生物统计等领域遇到的高维数据集还不太多，因此这种方法并未受到足够的重视，随着现代信息技术、互联网行业与生物信息学等的飞速发展，高维数据集大量涌现，以Lasso为代表的稀疏模型开始受到了广泛的关注。

在统计学中的变量选择领域Lasso具有极其重要的地位，然而学者们通过实验与理论分析发现，Lasso存在一些缺点，并针对Lasso的这些缺点进行了更深入的研究。Zhao等[2]指出其只在非常强的附加条件下才具有Oracle性质；SCAD模型[3]、MC模型[4]和自适应Lasso[5]等统计模型克服了Lasso的这一缺点，与Lasso相比，它们显著减小了对重要变量回归系数的压缩程度，因而这些模型具有所谓的Oracle性质；另外，Lasso在面对一组彼此之间存在高度相关性的解释变量时，往往只能选择出其中的一小部分，而针对上述缺点，Elastic Net能够将一组存在高度相关性的变量同时选中[6]；Lasso只能实现分散的变量选择，但很多情形下变量之间存在某种结构，如在基因微阵列分析中，某基因上往往会有多个变异点，在识别究竟是哪个基因的变异与所发生的疾病存在关联关系时将属于同一个基因的变异点分为一个组是更加合理的，因此有学者考虑将变量之间存在的结构作为先验信息再进行变量选择，Group Lasso是将变量的组结构作为先验信息的稀疏模型，其具有变量组选择功能[7]；除了应用于统计学上的变量选择问题，Lasso等稀疏模型还被应用到了压缩感知、信号重构和图像重构等诸多领域，在生物统计、机器学习、数据挖掘、图像处理和信号处理等领域有着越来越广泛的应用。

然而，Lasso和Group Lasso均忽略了下述情景：在实现变量组选择的同时实现组内分散的变量选择，即双层的变量选择问题，如何既实现变量组水平上的稀疏性，同时实现变量组内变量水平上的稀疏性。如在遗传关联研究中，每个基因上都有多个变异点，这些位于同一个基因上的变异点自然应该被视为位于同一个分组，因而希望在识别出与疾病发生相关的变异基因的同时也识别出基因内部与疾病发生相关的变异点，这就是双层变量选择问题。简言之，双层变量选择即同时实现组稀疏性和组内变量稀疏性。本研究基于Logarithm罚[8]提出了一种能够实现双层变量选择，即具有双层稀疏性的稀疏模型—Group Logarithm模型。

1 Logarithm罚

Logarithm罚的形式为

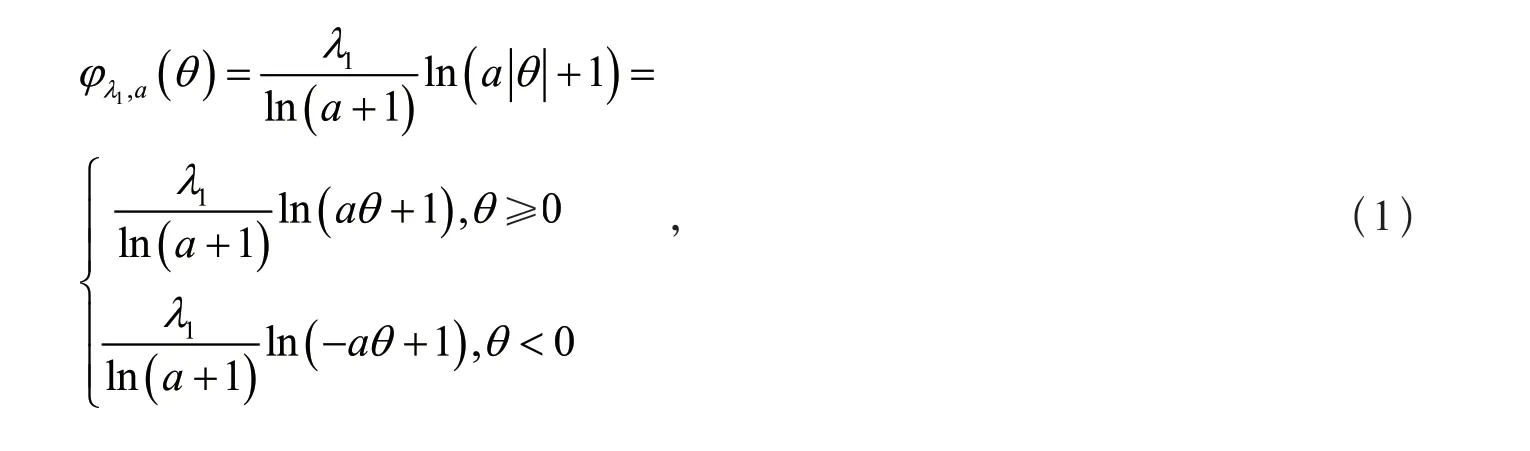
其中λ1>0且a>0。

当λ1=1时，Logarithm罚的函数图像如图1所示。图1中的虚线和直线分别表示a=1和a=0.1对应的两种情况，点虚线表示L1范数罚的图像。由Logarithm罚的图像可以看出，当a→0时Logarithm罚趋于L1范数罚。随着系数绝对值的增大，Logarithm罚的惩罚力度逐渐降低，即逐渐减小对变量系数的压缩程度，这与上文中所提到的SCAD罚和MC罚的原理类似，这种性质能够有效地减小对回归系数估计的偏差。

图1 Logarithm罚图像

2 Group Logarithm模型

2.1 Group Logarithm模型的形式

已知如下的线性回归模型：

式中：β为P×1维的系数向量；X为n×P阶的设计矩阵；y为n×1维的输出向量；噪声服从高斯分布，即

事先将P个变量划分为J个组，βj代表第j个变量组对应的系数向量，Xj代表第j个变量组对应的子设计矩阵，j∈ {1 ,2,… ,J}。假设数据被标准化其中xijp表示对第j个变量组中的第p个变量的观测值，则Group Logarithm模型为

式中：dj为第j个变量组所含的变量数；外层的函数fout为Logarithm罚；内层的函数为L1范数罚。双层罚函数的形式使得Group Logarithm模型具有双层变量选择能力，因而其既能选择出目标变量组，又能选择出目标变量组内的目标变量。

2.2 Group Logarithm模型的求解算法

本文利用局部坐标下降算法（local block coordinate descent algorithm，LBCDA）[9]求解Group Logarithm模型。局部坐标下降算法与坐标下降算法类似，每次只对单个变量进行优化，不断循环迭代每个变量直到算法收敛从而得到最终的解。局部坐标下降算法利用了MM（majorize minimization）算法的思想，解决了Group Logarithm不具有关于单变量显式解的问题。

由于Logarithm罚在[ 0,+∞)上是凹函数，所以Logarithm罚与其在当前点处的一阶泰勒展开式满足如下关系

上述等号成立是因为剔除常数项后不影响优化问题的最优解。则关于第j个变量组的优化问题变为

式（9）实际上是一个求解Lasso的问题，此时可用坐标下降法求解。由于式（9）在0处不可微，令其中

利用子梯度（subgradient）和子微分（subdifferential）可得式（9）关于单变量的显式解为

下面给出求解Group Logarithm的局部坐标下降算法：

1） 输入响应向量y、设计矩阵X、回归系数向量的初始值β；

② 当p=1，2，…，dj时，重复执行下列步骤：令利用式（11）求解βjp；令p=p+1；更新βjp；

③ 令j=j+1。

3） 得到遍历一次全部分组后的回归系数向量β，判断是否满足预先设定的收敛条件或迭代次数，若不满足则跳转到第2步；满足，结束算法。

4） 输出回归系数向量β。

3 数据集实验

本研究求解Group Logarithm模型选择了局部坐标下降算法，该算法将坐标下降算法和MM算法结合，每次只对单个变量进行优化，且每次关于单个变量求解一次优化的计算复杂度仅为O（m），不断循环迭代每个变量直到算法收敛从而得到最终的解。该算法与近似梯度方法及ADMM（alternating direction method of multipliers）方法等相比，计算开销更小，在具体的实验中也显示该算法在求解Group Logarithm模型时速度较快，当变量和样本均不超过600个、计算机配置为intel i5 CPU和8 GB内存的硬件条件下，可在数十秒内得到计算结果。下面具体阐述本研究提出的Group Logarithm模型的稀疏性效果。

3.1 双层稀疏性

为了验证Group Logarithm的双层变量选择能力，选择人工数据集所做的30次实验中的第一次实验，该次实验拟合出的非零回归系数见表1。人工数据集中各变量的分组情况及其真实系数值如下：

表1 三种方法的回归系数对比表

从三者的实验结果对比可以看出：Lasso只实现了分散的变量选择；Group Lasso只实现了变量组选择，被分为同一个变量组的变量的系数同时为零或同时非零；Group Logarithm实现了组内的变量选择，同一个分组内的变量系数有的为零、有的非零。Group Logarithm的变量组选择能力可以从其实验结果与Lasso的实验结果对比看出：V40的真实回归系数为0.3，为期望被选中的目标变量，Lasso选中了V40，而Group Logarithm得到的V40的回归系数值为0，其没有选中V40，原因为在Group Logarithm中V40与其他V31—V39这9个真实回归系数为零的非重要变量位于同一个变量组，大量非重要变量的存在导致该变量组为非重要的变量组，V40受到这9个同组中非重要变量的牵扯，导致其没有被选中，也就是说Group Logarithm中属于同一个组的10个变量同时没有被选中，即实现了组稀疏性和变量组选择。总之，从Lasso、Group Lasso和Group Logarithm的实验结果可以看出，Group Logarithm既实现了变量组选择，又实现了组内的变量选择，具有双层的变量选择能力。

3.2 预测的准确性

3.2.1 人工数据集实验

该数据集包含2n=600个样本和P=500个变量，这500个变量被划分为53个变量组。该数据集中各变量的分组情况及其真实系同式（12）。对于上述人工数据集，将其变量随机划分成两个样本数相等的子数据集，其中一份作为训练数据集，另一份作为测试数据集，将上述划分过程重复30次，得到30个实验结果，取30次实验结果的均值作为最终的实验结果。人工数据集实验结果如表2所示。表2中：n表示训练样本数；P表示变量总数；Size表示选出的变量总数；Rel表示识别出的目标变量数；Noi表示剔除的冗余变量数；MSE表示预测均方误差（mean square error，MSE）。从人工数据集实验结果可以看出：与Lasso和Group Lasso相比，Group Logarithm的预测均方误差值MSE更小，因而其具有更好的预测准确性；Group Logarithm选中的变量数目最少，与Lasso和Group Lasso相比具有更好的稀疏性。

表2 人工数据集实验结果

3.2.2 真实数据集实验

采用来自Homer与Lemeshow收集的新生儿体重数据集（birthweight dataset）[10]进行实验，将189个变量随机划分成两个分别含有100个样本和89个样本的子数据集，令其中含有100个样本的子数据集作为训练数据集，含有89个样本的子数据集作为测试数据集，将上述划分过程重复100次，得到100个实验结果，取100次实验结果的均值作为最终的实验结果。实验结果如表3所示，从表3可以看出，与Lasso和Group Lasso相比，Group Logarithm具有更高的预测准确性和更好的稀疏性。

表3 新生儿体重数据集的实验结果

4 结论

本研究提出了一种新的双层变量选择稀疏模型—Group Logarithm，其基于双层结构的罚函数，内部利用可实现组内稀疏性的L1范数罚，外部利用Logarithm罚。Group Logarithm既能识别出海量变量中重要的变量组，又能识别出重要变量组内重要的变量。通过人工数据集实验验证了其双层变量选择能力，并且人工数据集实验和真实数据集实验表明，与Lasso、Group Lasso等稀疏模型相比，Group Logarithm具有更好的预测准确性和稀疏性，显示了其在人工智能、机器学习和数据挖掘等领域具有良好的应用前景。