基于改进集合经验模态分解的滚动轴承故障诊断

李 萌

(长春大学 机械与车辆工程学院，长春 130022)

滚动轴承作为旋转机械中最常见的零部件被广泛地应用于生产生活中，但它也是最容易损坏的机械元件之一。由于轴承长期在高温、高速等恶劣条件下工作，致使整个旋转机械中有超过30%的故障是由滚动轴承信号所引起的[1]。因此，滚动轴承故障诊断在整个机械生产设备系统中显得尤为重要。

小波分析法和经验模态分解(EMD)方法是目前轴承故障诊断最常用的两种时频分析法，由于小波分析法需要人为地选择小波基函数，所以，EMD方法成为研究该非平稳信号的首选，但EMD方法在分解过程中又会产生边界效应和模态混叠现象。为了消除EMD产生的边界效应和模态混叠现象，提出一种改进的自适应白噪声的完备集合经验模态分解(CEEMDAN)结合能量特征的故障特征提取方法，再通过WOA-SVM来进行故障模式识别。

1 滚动轴承故障信号特征提取

EMD方法是一种处理滚动轴承非平稳信号的方法，它是一个自适应频率的筛选过程，依次分离出高频、次高频和低频固有模态分量。但是对原始信号进行分解时会产生两方面不足：一方面是在样条插值产生包络线时，会产生边界效应；另一方面是在分解信号时会发生相同IMF分量出现不同频率信号或者不同IMF分量出现相同频率信号的现象，也叫模态混叠现象。

EEMD方法的分解效果虽然比EMD有了很大地改善，但是此方法增加集成的次数降低重构误差，使得提取信号特征的效率大大降低。在此基础上，一种具有自适应白噪声的完备集合经验模态分解方法(CEEMDAN)被提出[2]，它在分解过程中自适应地添加高斯白噪声序列，再通过计算唯一的余量信号来得到分解的各个固有模态分量，解决了EEMD分解后剩有残余噪音和提取效率低的问题。

设原始信号为x(t)，第i次试验中添加高斯白噪声序列为ni(t)，则得到了添加第i次噪声后的信号xi(t)：

xi(t)=x(t)+ni(t)i=1,2,…,I，

(1)

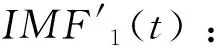
(2)

(2)计算当k=1时分解后的余量信号r1(t)：

(3)

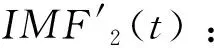
(4)

(4)分别对k=2,…,K重复步骤(3)，分解得到第k+1个IMF分量：

rk(t)=rk-1-IMFk(t)

(5)

(5)继续执行上述步骤直到获得的余量信号再也不能分解为止，此时，IMF分量总个数为K，且最终的余量信号为：

(6)

因此，原始信号x(t)通过CEEMDAN分解得到各个分量表达式为：

(7)

由上述过程可知，CEEMDAN分解过程具有完整性，可以精确重构信号，同时，通过调整高斯白噪声标准差εk，可以在每一分解过程中选择不同的信噪比达到自适应的分解过程。

2 滚动轴承故障信号模式识别

鲸鱼优化算法(WOA)是一种元启发式优化算法，在2016年被Seyedali Mirjalili等人提出[6]。它与其他优化算法相比，采用随机或最佳搜索代理来模拟鲸鱼觅食行为，并使用螺旋来模拟鲸鱼泡泡网的攻击体制，所以具有收敛速度快、调节参数少、结构简单等特点。WOA算法主要包含环绕包围猎物、螺旋更新位置和全局搜索猎物等三个阶段。

(1)环绕包围猎物

鲸鱼得到猎物群信息后将其包围，假设最佳猎物个体在目标群体附近，则鲸鱼位置更新公式如下：

D=|C·X*(t)+X(t)|，

(8)

X(t+1)=X*(t)-A·D，

(9)

A=2a·r-a，

(10)

C=2·r，

(11)

(12)

式中：X(t)为鲸鱼当前位置，X*(t)为经t次迭代后鲸鱼的最佳位置，A和C为系数向量，r表示[0,1]的随机向量，a表示从2到0的线性递减因子。

(2)螺旋更新位置

当鲸鱼发现目标猎物时，会以螺旋上升的方式捕食猎物，表达式为：

X(t+1)=D′·ebl·cos(2πl)+X*(t)，

(13)

D′=|X*(t)-X(t)|，

(14)

(15)

式中：D′为鲸鱼到目标猎物的最佳距离，b为常数，l为[-1,1]的随机数，p为[0,1]的随机数。

(3)全局搜索猎物

鲸鱼也可以通过随机搜索来进行全局搜索猎物，当系数向量A的绝对值大于等于1时，可以用随机搜索猎物来代替最佳位置搜索猎物，以便于找到更为合适的取值，其表达式为：

X(t+1)=Xrand(t)-A·D，

(16)

D=|C·Xrand(t)-X(t)|，

(17)

式中：Xrand(t)为鲸鱼群中随机选择的一个个体的位置。

通过上述WOA算法便可以优化SVM中的惩罚因子c和核函数g，解决传统人工试验过程繁琐，诊断效率低等问题，提高SVM识别的正确率。

WOA-SVM具体算法流程如图1所示。

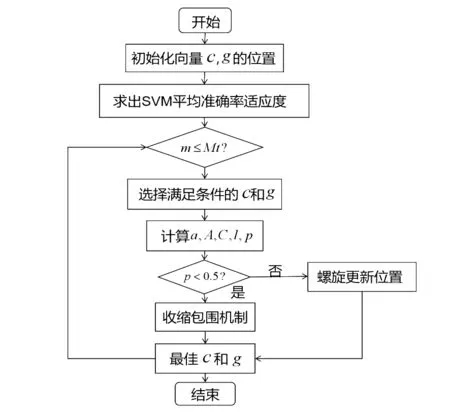
图1 WOA-SVM算法流程图

3 实验及结果分析

3.1 仿真信号建立及模态分解

针对CEEMDAN分解方法是否有效解决EEMD分解中存在的模态混叠现象和重构误差大的问题，构建一组仿真信号S如图2所示，其中，S=x1(t)+x2(t),x1(t)=5cos(100πt),x2(t)为强度0.2的高斯白噪声，取1 024个采样点。

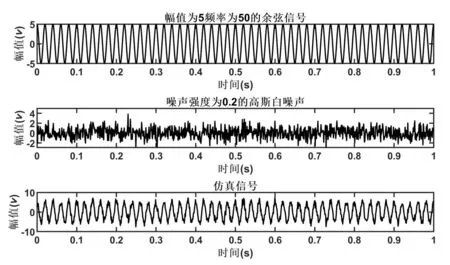
图2 仿真信号波形图

对仿真信号S分别进行集合经验模态分解(EEMD)和自适应噪声的完备集合经验模态分解(CEEMDAN)，由于仿真信号大部分的信息都集中在前几个IMF分量中，且为了清晰地呈现各个分量信号的特征，取前六个IMF分量示意图，如图3、图4所示。

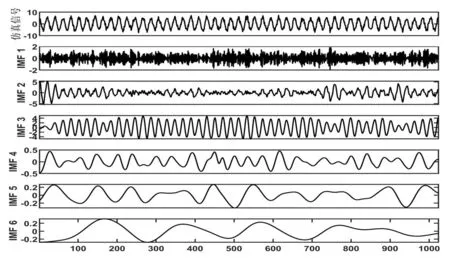
图3 EEMD分解示意图

图4 CEEMDAN分解示意图

在EEMD分解之前，我们设定加入白噪声的标准差为0.2，加入白噪声次数为100次，最大迭代次数为1 000次。由EEMD分解示意图可知，虽然IMF1和IMF3基本上恢复了仿真信号中的白噪声和余弦信号，有效地缓解了EMD的模态混叠现象，但是在IMF2中依然存在一定的模态混叠现象。

由图4可知，分解后的IMF分量按照从高频到低频的方式排列，故CEEMDAN方法克服了EEMD残余的模态混叠现象，可以用来分解信号；且从图5来看，CEEMDAN分解的各IMF分量重构误差与EEMD的比值约有10-15倍，重构误差几乎等于零，故CEEMDAN方法有效地克服了EEMD模态混叠现象和重构误差大的问题。

图5 重构误差示意图

3.2 滚动轴承故障诊断实例

为了进一步验证该方法的有效性，采用6310型向心球轴承在滚动轴承故障诊断台上进行故障模拟实验，如图6所示。在信号采集过程中，电机转速为1 350 r/min，采样频率为10.24 KHz。对滚动轴承的正常、内圈故障信号和外圈故障信号分别进行采样，每种状态下各取40组数据，每组数据有1 024个样本点。将数据集分为训练样本和测试样本，首先选取正常状态轴承、内圈故障状态轴承和外圈故障状态轴承的各前20组数据作训练样本，最后选取它们的后20组作测试样本。

图6 滚动轴承故障诊断试验台

对经过CEEMDAN方法分解后的三种滚动轴承状态的信号分别进行能量特征提取，并进行归一化处理后得到的部分WOA-SVM故障诊断样本如表1和表2所示。

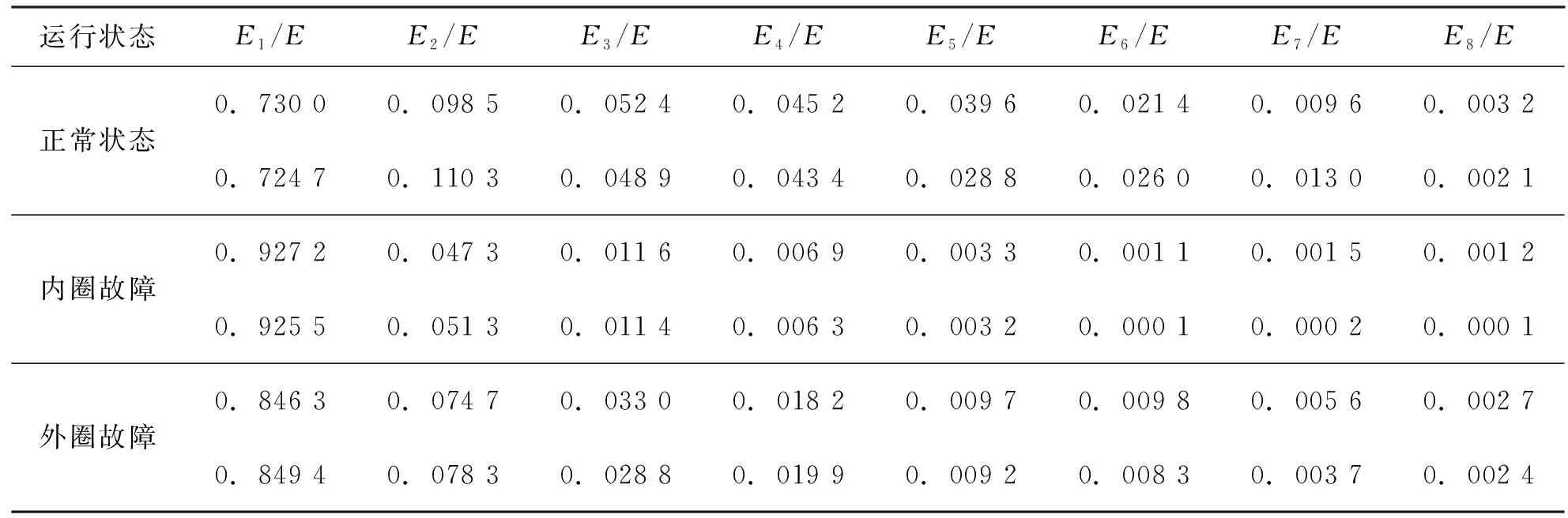
表1 支持向量机部分故障诊断样本表(训练集)

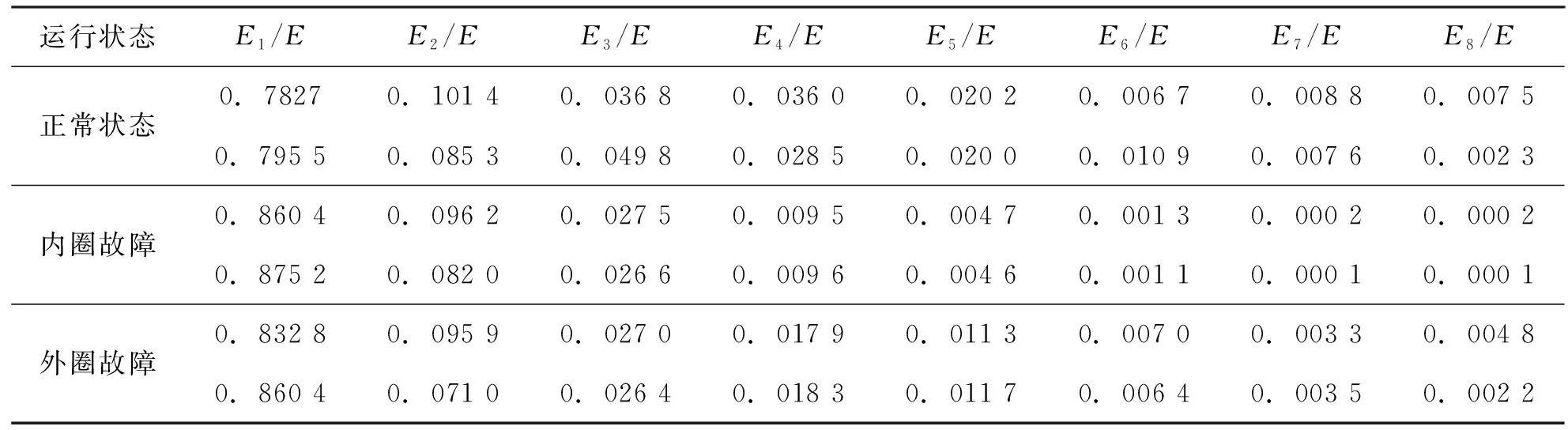
表2 支持向量机部分故障诊断样本表(测试集)

用训练样本分别训练支持向量机和参数优化后的支持向量机，再用测试样本分别测试训练得到的两种支持向量机，测试是否优化参数后的支持向量机准确率更高，得到的实验结果如表3所示。

表3 诊断结果对照表

由表3可知，在运算时间相差不大的情况下，通过鲸鱼优化算法优化支持向量机的参数可以有效地提高支持向量机的故障诊断准确率。

4 结语

EMD作为常用的模式识别方法，存在严重的模态混叠现象。我们采用一种基于EEMD改进的算法CEEMDAN，不但可以抑制模态混叠现象，而且能够精确地重构原始信号；再结合WOA-SVM进行模式识别，得到优于SVM的故障诊断识别率，从而验证了该方法的有效性。