基于自适应虚拟同步发电机系统的微网逆变器控制策略研究
徐大可,盛德刚,刘亮,洪祥
(南京大全电气研究院有限公司,江苏南京 211106)
随着我国节能减排政策和电力行业发展趋势的综合影响,分布式可再生能源并网发电赢得了大发展机遇。其中,分布式可再生能源并网的控制策略也得到了广泛研究,其中以电压源型换流器(voltage source converter,VSC)相关的矢量控制方法研究最为广泛,为多端柔性直流输电系统的远距离传输提供解决方案[1-2]。然而,用矢量控制的VSC 方法策略缺乏旋转惯性,系统易产生谐波,不能为交流系统提供稳定的电压和频率,增加电网运行不稳定的风险。为此,学者们给出了虚拟同步发电机(virtual synchronous generator,VSG)的控制理念,通过模拟同步发电机的惯量和阻尼特征来提高系统抗风险能力,从而保证系统电压和频率的稳定性。
目前,学者们对VSG 稳定性方面的研究主要在以下方面:一方面是对单台VSG 控制直流系统的稳定性进行研究。通常的研究方法是将直流系统设定为恒功率源或恒压源,此类系统相对来说比较简单。文献[2]通过利用传统无惯性的下垂控制方法和VSG 控制的组合形式,提出了VSG控制方法的下垂控制模式。文献[3]通过探讨一种新的解耦算法,以实现VSG 来控制有功和无功独立输出的目的。文献[4]通过对解耦算法的参数特性进行分析,提出了以保证系统运行稳定性为主要指标的设计方案。另一方面是对含VSG的多端直流系统进行研究。考虑到系统的复杂程度,通常结合系统稳定性分析方法进行讨论。文献[5]通过对传统的VSG 控制策略难以快速响应直流系统注入功率的变化情况进行详细分析,并由此提出限幅约束条件下的的VSG 控制直流系统母线电压的下垂控制模式。为了保证复杂系统的运行稳定性,已有的文献着重采用了模式分析和频域分析等方法。文献[6]结合模式分析法对交流系统运行的稳控参数进行了深入探讨,以此提出促进交流系统稳定运行的参数控制优化方案。文献[7]利用频域分析法分析了VSG 系统的控制方式和同步电机之间的谐振作用,并提出了一种一阶系统控制方案。文献[8]提出了一种新的阻尼控制方法,并结合实验结果论证了该方法可有效地提高系统低频振荡的稳定性。文献[9]基于物理原理设计出含VSG 系统的下垂控制模式,并根据模式分析法对交流系统稳定性影响进行了深入探讨。
综上所述,对于VSG 的多端柔性直流系统的稳定性研究方面存在着以下问题:当VSG 利用直流系统电压下垂控制后,多端直流系统中将出现新的振荡模式,将直流系统等效为恒定功率源进行分析是具有一定局限性的。下垂控制的主要原理为通过模拟同步发电机的有功和频率、无功和电压之间的下垂关系,使其控制下的微源在未有高频通信的基础上能完成负荷分配的方式,但下垂控制方法根本上并不能解决分布式电源的惯性问题,即该组成系统仍是“弱惯性”系统[10-11]。
基于此,将根据荷电状态调整下垂系数的方法拓展到VSG 控制之中,通过引入自适应下垂特性的概念,使用平移下垂特性的方法对VSG 控制做了进一步改进,改进后的VSG 控制减少了对系统稳定性的影响,更有利于实现有功功率的合理分配与荷电状态的快速调整,通过Matlab/Simu⁃link 工具进行建模仿真,结果验证所提自适应VSG控制策略的合理性。
1 虚拟同步发电机系统传统的下垂控制思想
虚拟同步发电机系统传统的下垂控制思想可大致分为3 种形式:1)利用电流变量参与控制的V—I下垂策略;2)利用功率变量参与控制的V—P下垂策略;3)利用V2—P下垂策略。其中,本文重点探讨V2—P控制策略进行含VSC 换流站模型的研究。VSC 换流系统的功率平衡简易模型如图1所示。
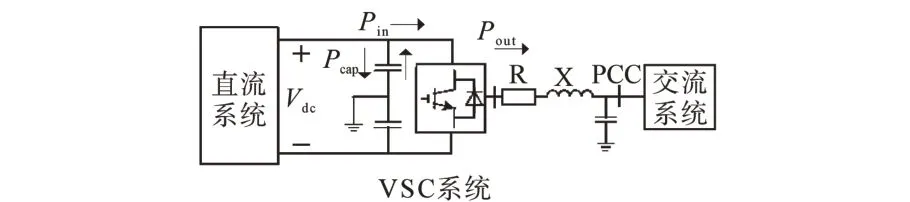
图1 VSC内部功率平衡简易模型Fig.1 Simple model of VSC internal power balance
图1 中,Vdc表示换直流系统的母线电压;Pin,Pout分别表示直流系统输入功率和换流站输出功率;Pcap表示直流电容存储/释放的功率;R,X 分别表示换流系统交流母线到公共连接点(point of common coupling,PCC)间的线路等效电阻和电抗。
建立VSC换流系统内的功率平衡方程为
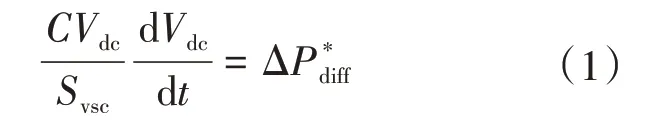
式中:C为换流系统的电容值;Svsc为换流站的额定容量。ΔP*diff为换流系统输入输出功率差的标幺值。
结合文献[12]所述,V2—P下垂控制原理可如下表述:当换流站的输入功率Pin和输出功率Pout因扰动而失去平衡状态时,其功率偏差可由直流电容进行补偿,见式(1)。在此过程中换流站的直流电压也将所有变化。因此,V2—P下垂控制策略选择直流电压的平方差作为换流站的输入控制信号,通过计算附加输出功率结果来调节换流站的功率输出,保证直流系统电压在许可范围内运行。其所需计算的附加输出功率见下式:
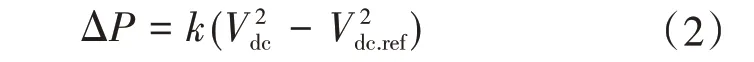
式中:k为下垂系数;Vdc.ref为直流系统参考电压值;ΔP为换流站所需调整的参考功率。
结合文献[13-14]阐述的d-q双环解耦控制的原理上,本文增设下垂控制模块,以此来建立完整的V2—P下垂控制模块。鉴于电压源换流器的多端柔性直流输电系统(voltage source converter based multi-terminal direct current,VSC-MTDC)内各换流站的直流母线电压数值上接近,可近似认为VSC-MTDC 中各换流站间的功率分配可由下垂系数k控制,其控制原理图如图2所示。
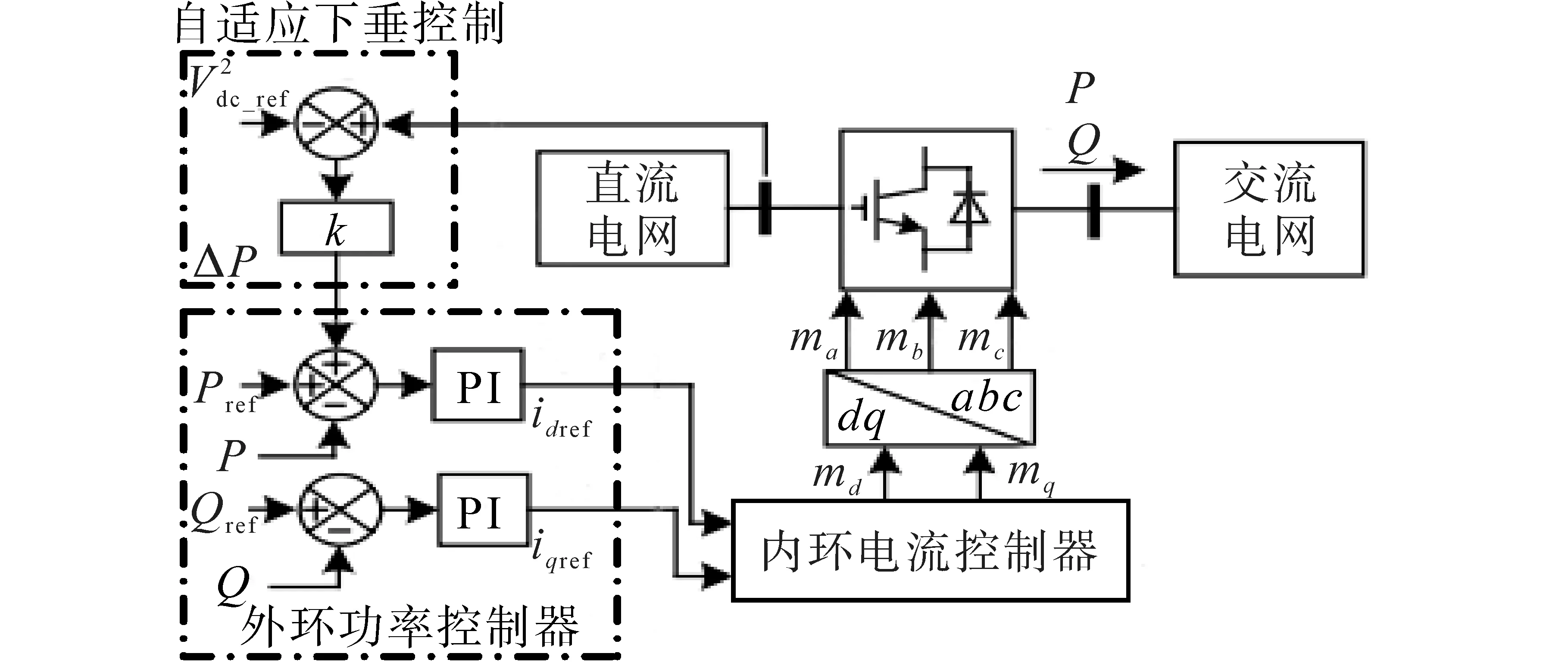
图2 V2-P 下垂控制器Fig.2 V2-P droop controller
图2 中,Pref,Qref分别表示换流站输出的参考功率;P,Q分别为换流站实际输出功率;idref,iqref分别表示d轴和q轴的参考电流;md,mq分别表示d轴和q轴的调制信号;ma,mb和mc分别表示三相调制解调信号。
2 基于虚拟调速器的虚拟同步发电机控制策略
换流站和同步发电机存在类似的功率平衡关系,如图3所示。其中,将公共连接点作为系统的平衡参考点,设PCC 处母线电压为U∠0°,VSC交流侧母线和同步发电机侧电压均设定为E∠δ,原动机的机械功率设定为Pm,其相应的转子动能设为Ek,同步发电机输出的额定功率设为Pe。同步发电机的功率平衡方程可利用转子运动方程来阐述:
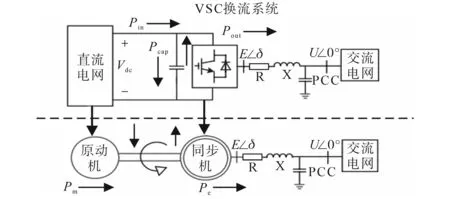
图3 换流系统和同步发电机的功率平衡对比Fig.3 Comparison of power balance between commutation system and synchronous generator
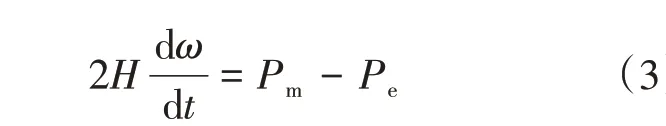
式中:H为发电机组的惯性时间常数;ω为发电机转子的角速度。
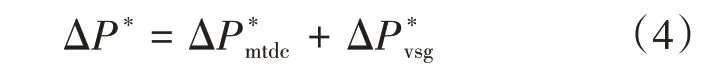

式中:Hvsc为发电机的虚拟惯性时间常数;ω*为换流站交流侧实测角频率。
当交流系统的角频率产生变化时,控制器将产生ΔP*vsc用来调整换流站的输出功率和补偿阻尼角频率的变化。
为求解出虚拟调速器的附加功率变化量ΔP*mtdc,需建立系统角频率和直流母线电压的耦合关系,对式(1)和式(3)的左侧部分建立等式并计算积分[15],则有:
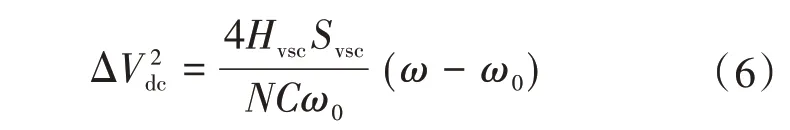
式中:N为换流站内直流系统的电容数目;ω0为系统的额定角频率;ΔVdc为直流母线电压的修正量。
对式(6)进行标幺化处理后,将其代入式(2)可得:
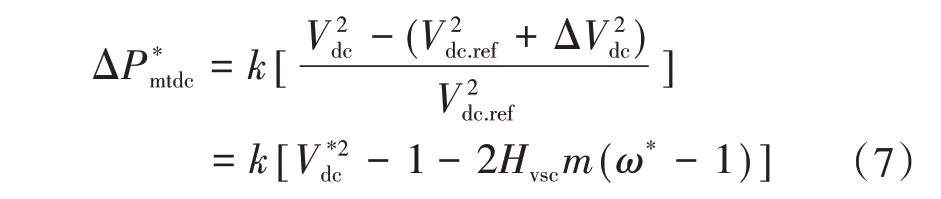
式中:V*dc为直流系统电压的实测值;k为放大系数;m为VSC和直流电容的容量比。
m的数值为直流电容时间常数的倒数,即
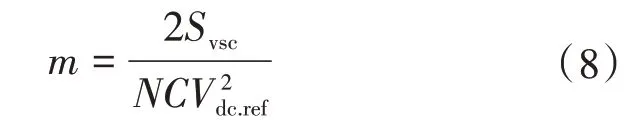
式(7)则为本文设计的虚拟调速器控制模块,其控制原理如图4所示。
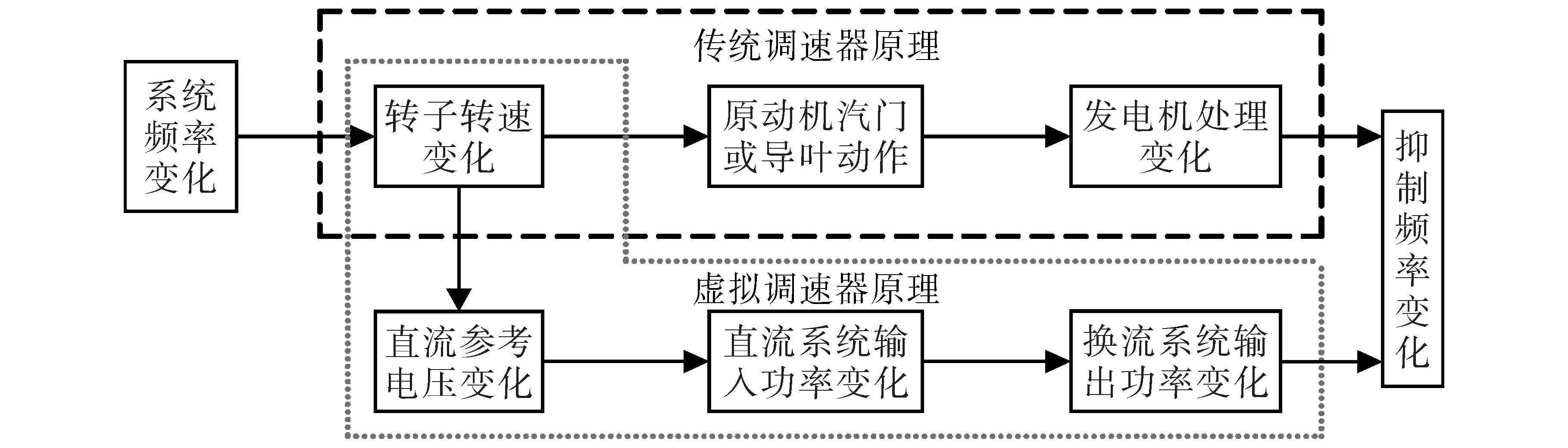
图4 虚拟调速器原理图Fig.4 Virtual governor schematic
结合式(7)和图4可知,虚拟调速器可以根据交流电网的频率变化自动对换流站的输出功率进行调整,从而达到抑制系统频率偏移和波动的效果。
综上分析,虚拟转子运动方程为
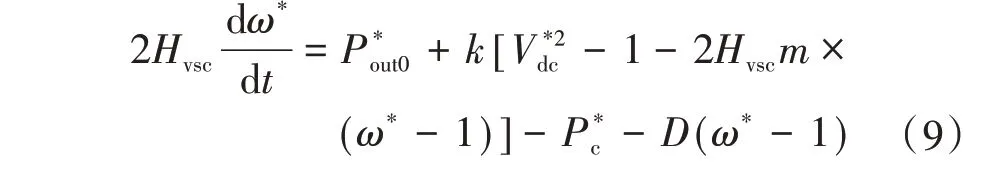
式中:P*out0为换流站输出功率的初始值;D为虚拟阻尼系数。
设计的虚拟同步机控制器如图5所示。
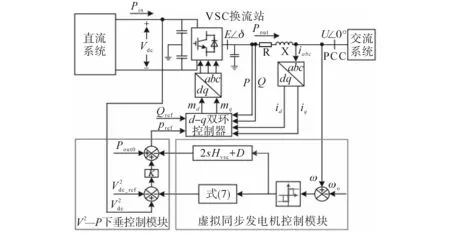
图5 虚拟同步电机控制模块Fig.5 Virtual synchronous motor control module
由式(9)和图5可知,换流站的功率输出是由直流母线电压和交流系统频率共同决定的,因而AVSG 控制策略可兼顾VSC-MTDC 控制系统直流电压和电网频率的稳定性指标。当交流系统发生扰动或故障时,AVSG 控制策略将对VSC-MT⁃DC 系统内各换流站的功率分配进行自动调整,并模拟出同步发电机的输出功率,补偿电网波动的频率差并抑制系统振荡阻尼,无需建立站间通信方式,确保直流母线电压在合理范围内变化,不会出现VSC-MTDC系统电压越限的情况。
3 AVSG改进控制策略
鉴于以上探讨的VSC-MTDC 模型中换流站之间的功率分配方法是按照下垂系数k进行比例控制的,结合文献[15]所述的分段式下垂特性原理对本文的下垂控制系数进行如下改进。
将AVSG 策略中的下垂特性曲线分成含角频率上、下限阈值[16]的水平段和含区间的斜线段两部分,设定其斜率为k1,其值由最大频差和发电机输出功率综合决定,并随发电机出力进行相应动态调整,如图6所示。
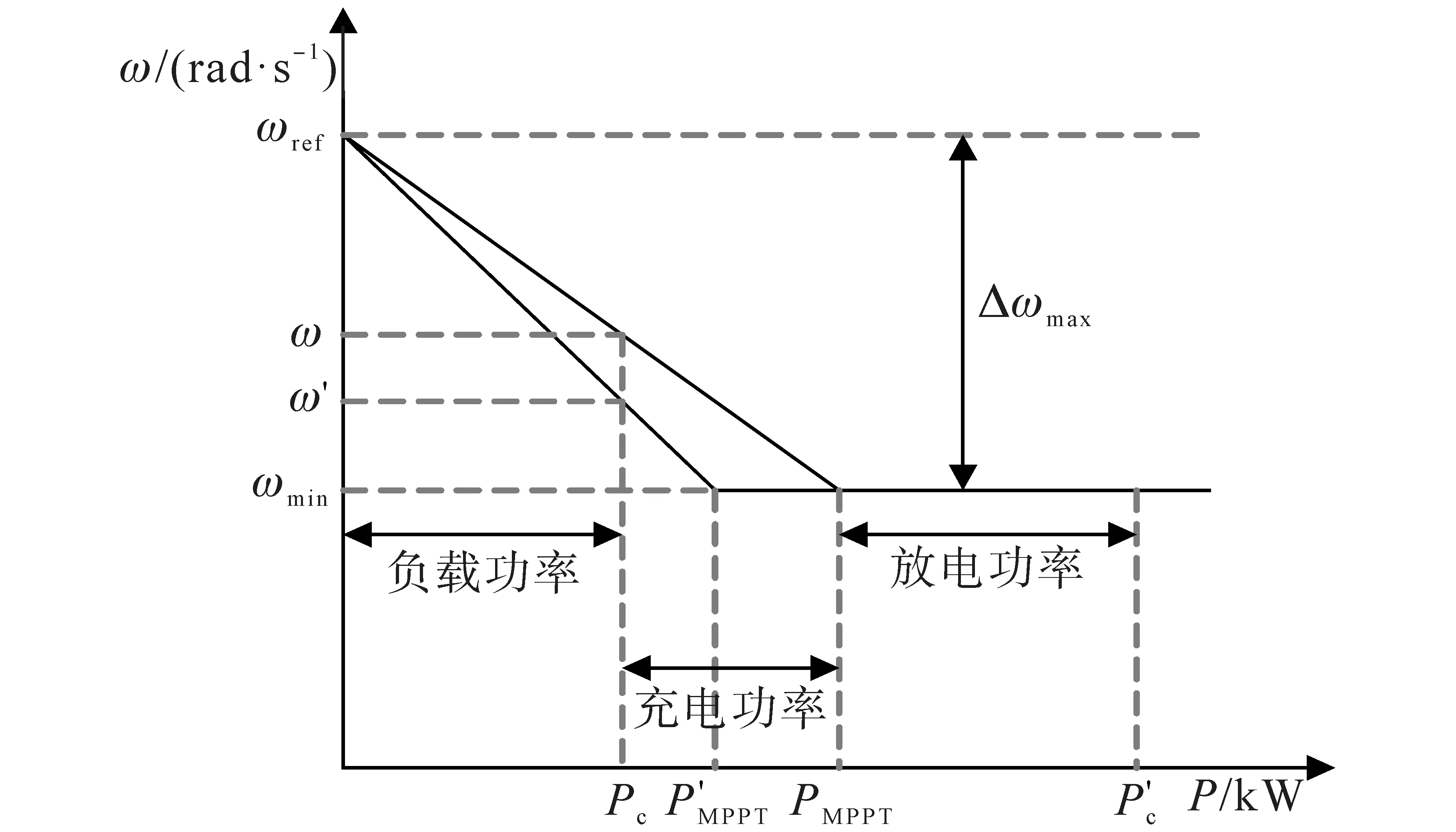
图6 自适应分段式下垂控制特性曲线Fig.6 Adaptive segmented droop control characteristic curve
当同步发电机的输出功率无法支撑微网系统的有功负载时,VSG 控制系统会直接调到下垂特性的水平直线段控制区间,控制直流电容放电来补充功率差额,其设计原理控制流程如图7所示。
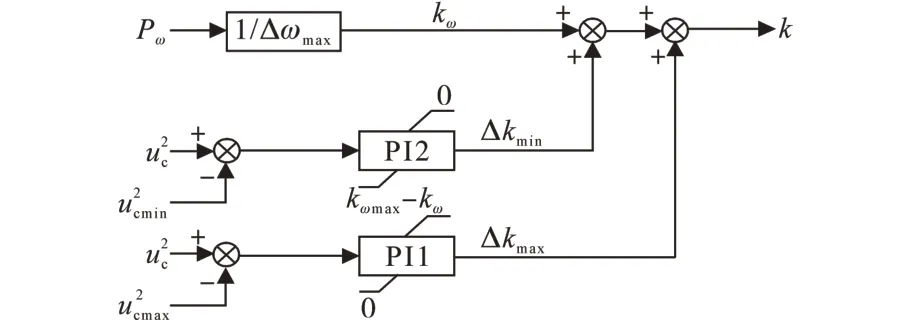
图7 自适应下垂控制系数的AVSG模块Fig.7 AVSG module with adaptive droop control coefficient
将风电场的输出功率和系统角频率偏差的最大比值设定为下垂控制曲线的对应斜率,利用VSG 系统的输出角频率的下限阈值ωmin设为下垂控制特性曲线的水平直线段,结合直流系统的端电压来反映直流电容器组的荷电状态,并分别设为直流电容器组的绝对和相对工作状态的电压界限阈值。
利用自适应下垂系数的AVSG 系统控制策略,根据直流电容器的荷电工作状态,本文选取以按照下垂系数承担负载为目标进行优化工作,其控制模式见表1。

表1 控制模式Tab.1 Control mode
3.2 自适应调整下垂特性曲线
本文建立的自适应动态调整下垂特性的控制原理如图8 所示。当系统处于模式1 状态下工作时,可采用分段式下垂特性曲线进行协调控制。当系统从模式1 跳转到其他模式时,本文保持原有下垂控制曲线的斜率值,并对整个下垂控制特性曲线进行平移。
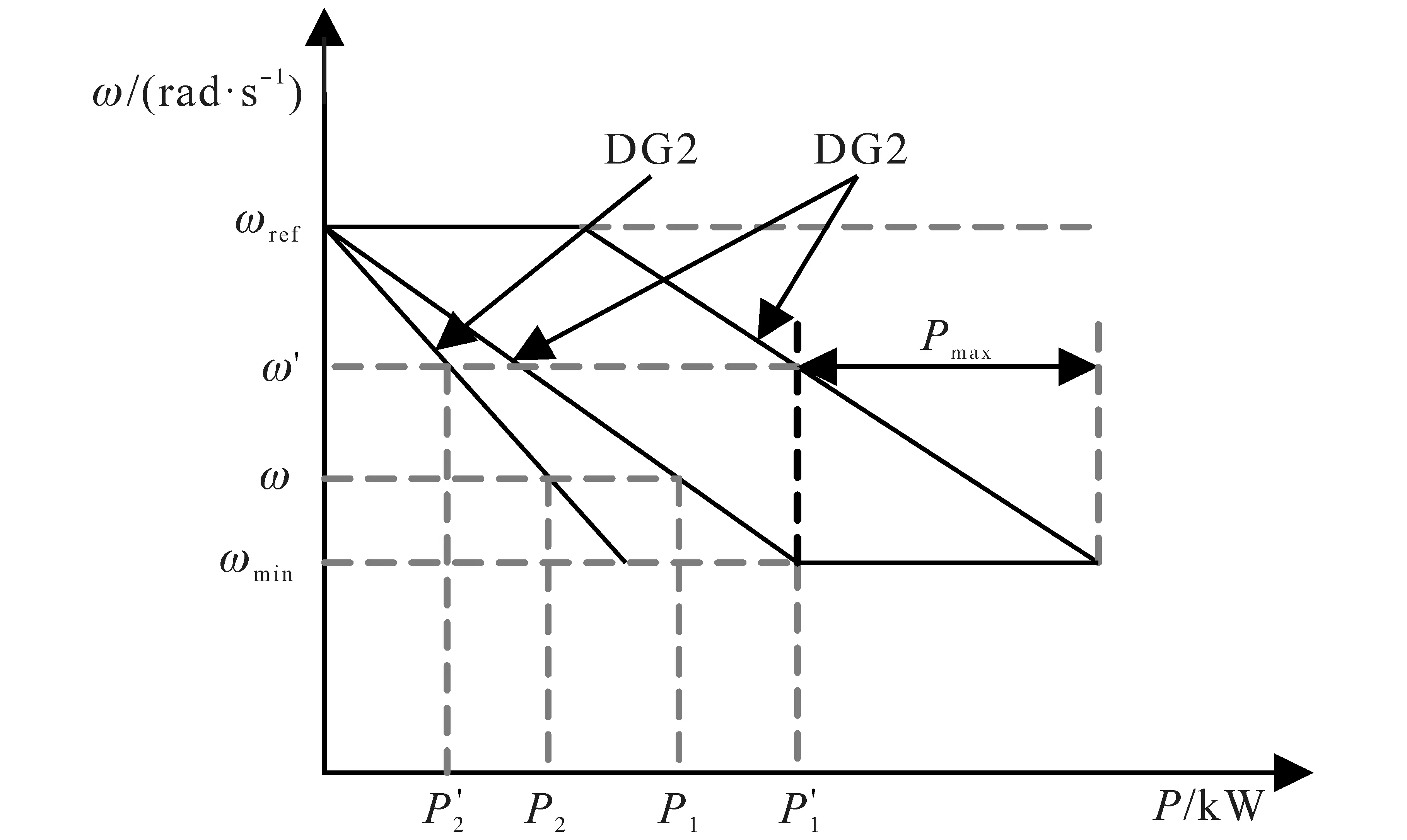
图8 自适应下垂系数调整方式Fig.8 Adaptive droop coefficient adjustment method
如图8 所示,在系统进入控制模式2 时,将下垂特性曲线水平向右进行平移,从而增加VSG 的有功输出;当系统处于模式3状态工作时,将下垂特性曲线水平向左进行平移,达到减小VSG 有功输出的目的,由差额功率的单元提供负荷供电。采用下垂控制特性曲线水平移动的方法能够重新调整系统运行点并合理分配有功,且能紧跟风电出力变化快速做出功率调整,从而有效避免下垂系数幅度调整过大带来的不利影响。
4 算例分析
为验证本文所提的基于自适应下垂控制系数的AVSG 模型的合理性,结合Matlab/Simulink仿真系统进行建模分析,模型主要包括:2个风电场、2 个风电换流站和2 个常规换流站。AVSG 系统的模型参数为:换流站额定容量450 MV·A,直流系统母线电压220 kV,交流系统电压110 kV,直流系统电容0.75 mF,线路电阻值0.01 Ω/km,线路电抗值0.5 Ω/km。 风电系统采用恒压定频控制方式,其系统模型的设计原则见文献[17]。对于AVSG 系统模型的控制方式选择自适应下垂系数控制方式。其中,分布式电源1有功输出为295 MW,分布式电源2有功输出为300 MW。风电场内配置的风电机组数目为20 台,单台容量设置为5 MV·A。
本文设计的自适应AVSG 控制系统主要设置四机系统和所供组成独立电网,负荷为300 MW,系统频率设置为50 Hz,分布式电源1 通过母线7并网,分布式电源2 通过母线12并网。模型如图9所示。
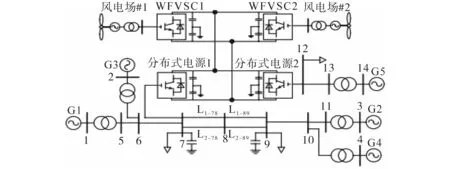
图9 双风电场多端送电系统Fig.9 Multi-terminal power transmission system of double wind farm
采用自适应AVSG 控制策略进行含VSC换流站模型的研究,并与传统下垂控制方法进行对比,其优化控制响应的效果如图10所示。
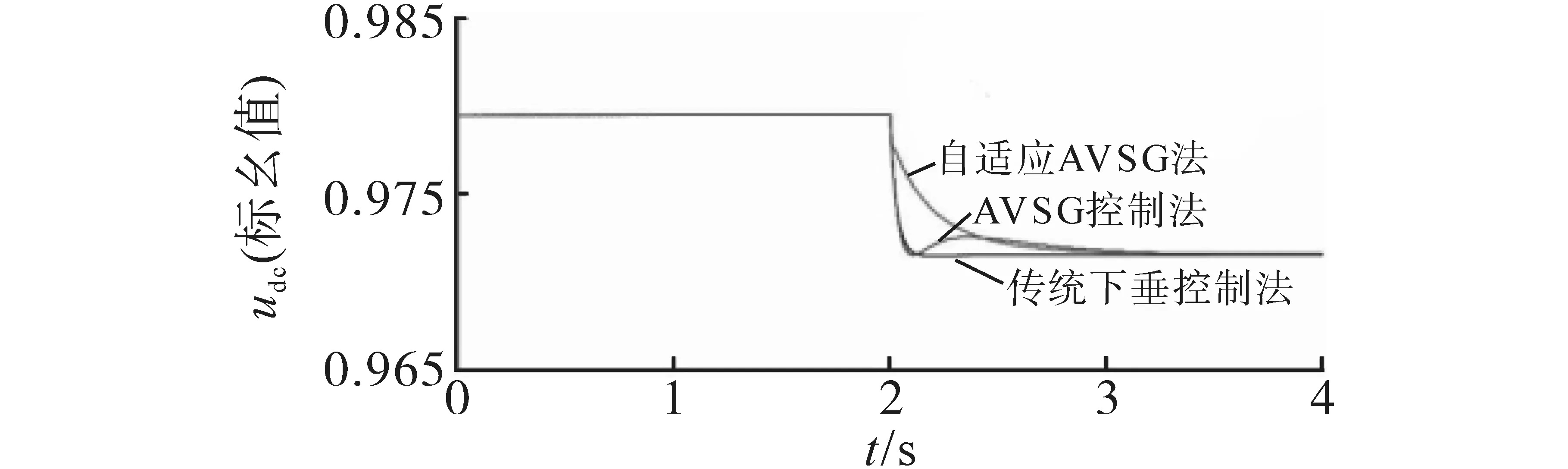
图10 不同控制策略下直流系统电压变化Fig.10 Voltage change of DC system under different control strategies
从图10 可看出,根据本文不同的控制策略,为了对系统负荷变化进行很好地功率平衡,均可采取直流系统的电压变化来进行相应调节,从而保证系统电压调整到新的平衡态。若单独采用传统下垂控制的方法,考虑该方法的弱惯性特点,当系统负荷突然增加时,直流系统的电压会迅速降低。利用本文的基于自适应下垂控制系数的AVSG 控制方法后,直流系统的母线电压会逐渐缓慢降至新的平衡态,说明该方法增加了系统惯性。
4.1 基于自适应下垂控系数的AVSG控制效果
当风电机组无法保证系统的功率平衡时,应通过直流系统提供所需的功率缺额,设定系统负荷在46~50 kW 间随机变化。其相应的仿真结果如图11~图13所示。
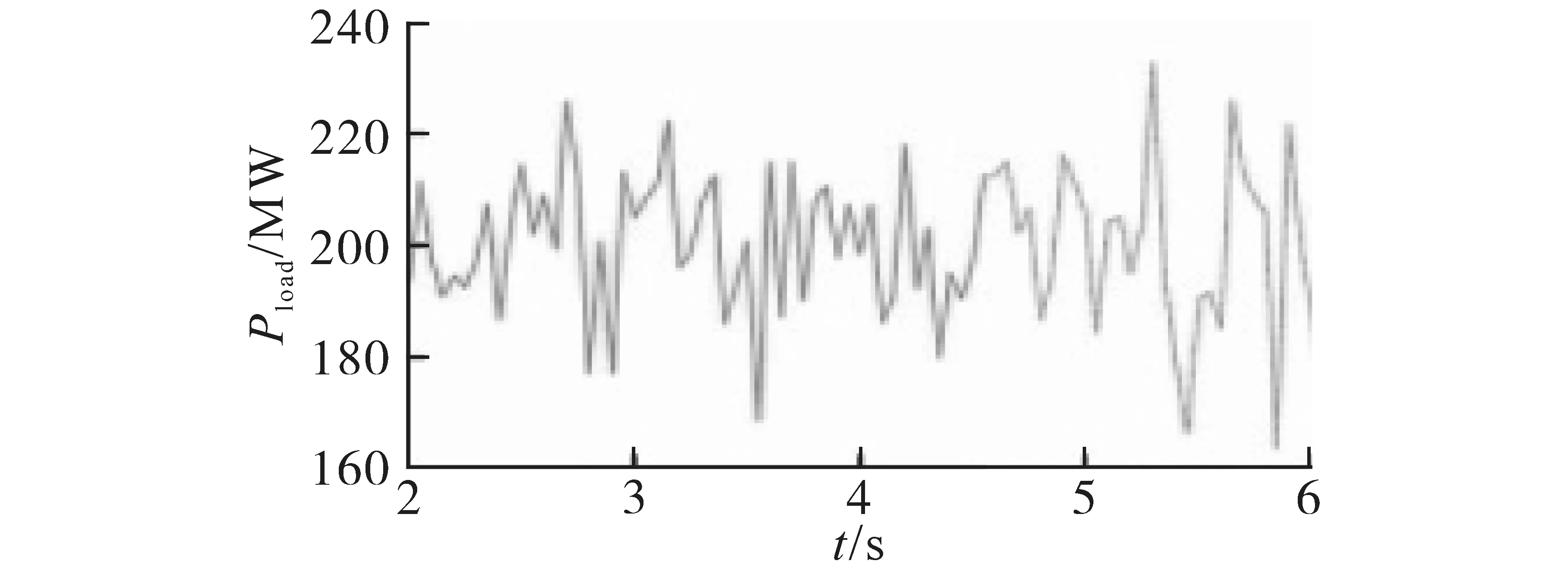
图11 短时间内系统负荷变化Fig.11 System load change in a short time
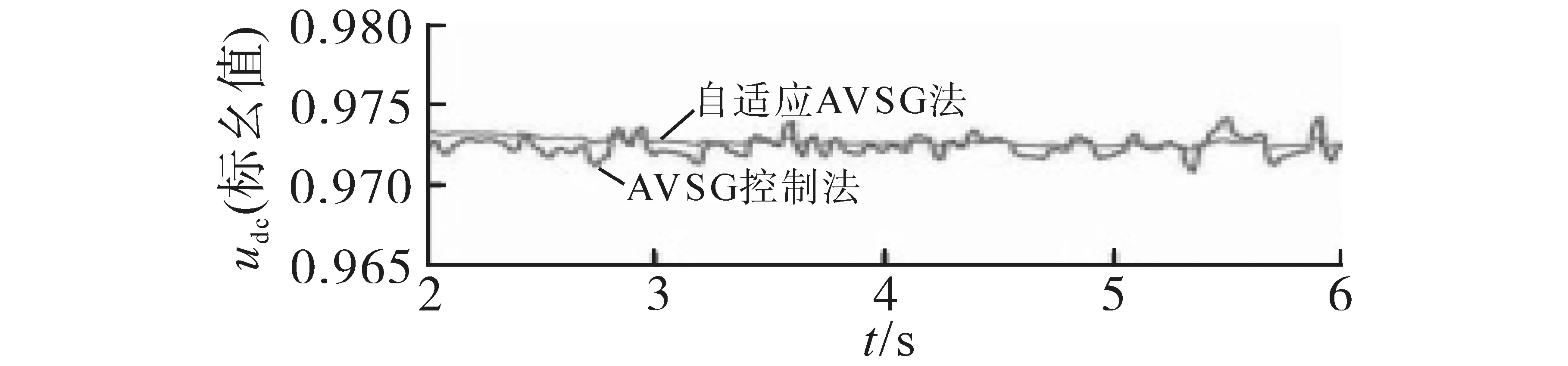
图12 直流系统电压响应变化Fig.12 DC system voltage response change
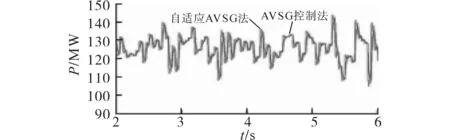
图13 直流系统输出功率响应变化Fig.13 DC system output power response change
从图11~图13 可看出,利用AVSG 控制方法时,随着系统负荷的变化,虽可保证系统运行稳定,但系统电压依然出现较大的波动;而采用基于自适应下垂控制系数的AVSG 控制方法后,可明显看出,在系统负荷较大波动的情况下,直流系统电压的质量也会得到明显改善;且从图13可发现,采用基于自适应下垂控制系数的AVSG 控制方法后,直流系统的输出功率响应更迅速,所提供的功率幅值更大,因此可以减小系统的功率偏差和直流系统的电压波动。因此所提出的自适应下垂控制系数的AVSG 控制方法可增加系统惯性,提高系统抑制电压波动的能力,从而改善了直流系统的电压质量。
4.2 基于自适应下垂控制系统对系统稳定性的影响
以下充分探讨系统受到扰动后恢复稳定运行的情况,以此来验证本文所提出的自适应AVSG 控制策略的合理性。在系统进行扰动试验前,将G1~G4 的电力系统稳定器(power system stabilizer,PSS)退出,投入自适应AVSG 控系统模块。设定线路L1-78在t=2.0 s 处发生三相瞬时故障,持续周期为5个周波时长,系统故障后恢复结果如图14~图16所示。
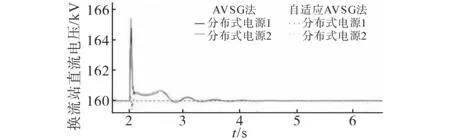
图14 发生故障时直流系统电压变化Fig.14 DC system voltage change in the event of a fault
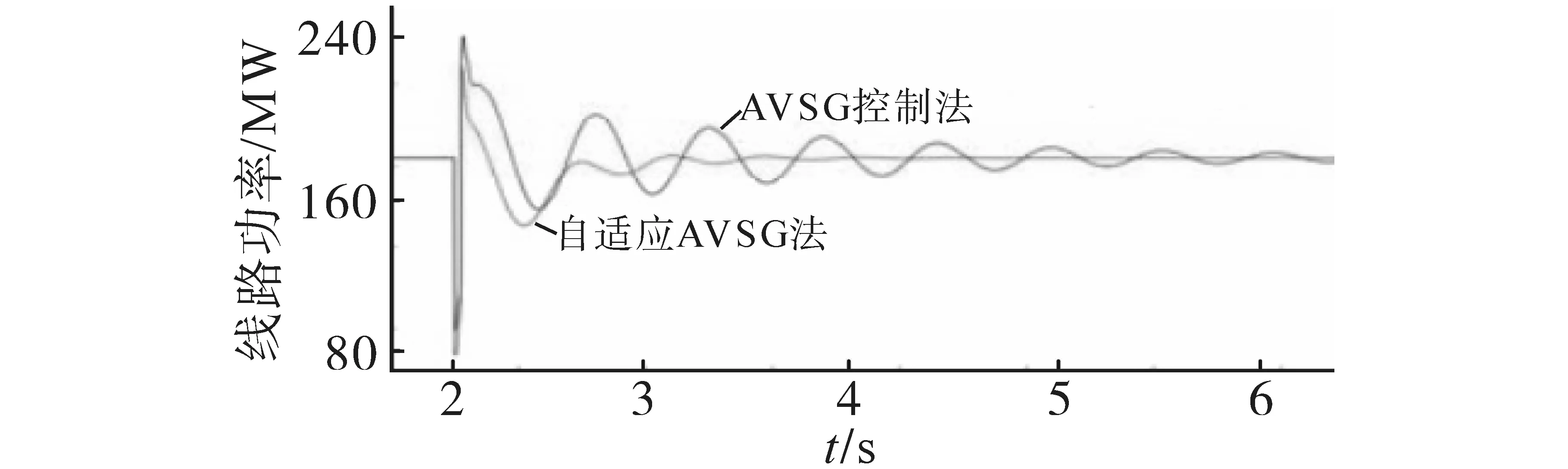
图16 发生故障时线路功率响应变化Fig.16 Line power response change in the event of a fault
由图14 可知,采用自适应AVSG 控制时,系统能够在故障发生后迅速地恢复到初始稳定运行状态上来,且直流系统的母线电压恢复到初始状态值。而由于交流系统抗扰动能力差的特点,使得传输线路L2-78上出现连续功率振荡的情况,如图15,直至6 s 后才渐趋稳定,但系统未能完全稳定。而采用自适应AVSG 控制策略时,直流系统的母线电压会随着转子角频率偏差自行追踪调整。且在故障时间内,同步电机的转子转速会陡增,直流系统电压也会急剧增大,利用自适应AVSG 控制模块可迅速降低有功输出,并结合直流系统电压限幅的作用,直流系统最高电压不超过1.05 标幺值,使其保持在允许范围内。并且分布式电源2 模块有功输出提高,直流系统电压会快速回落。在故障清除后,分布式电源1 的直流电压会继续追踪系统角频率进行自适应调整。因此在整个故障持续过程中,传输功率振荡和发电机转速振荡均能被有效抑制,并在6 s 后系统恢复稳定。
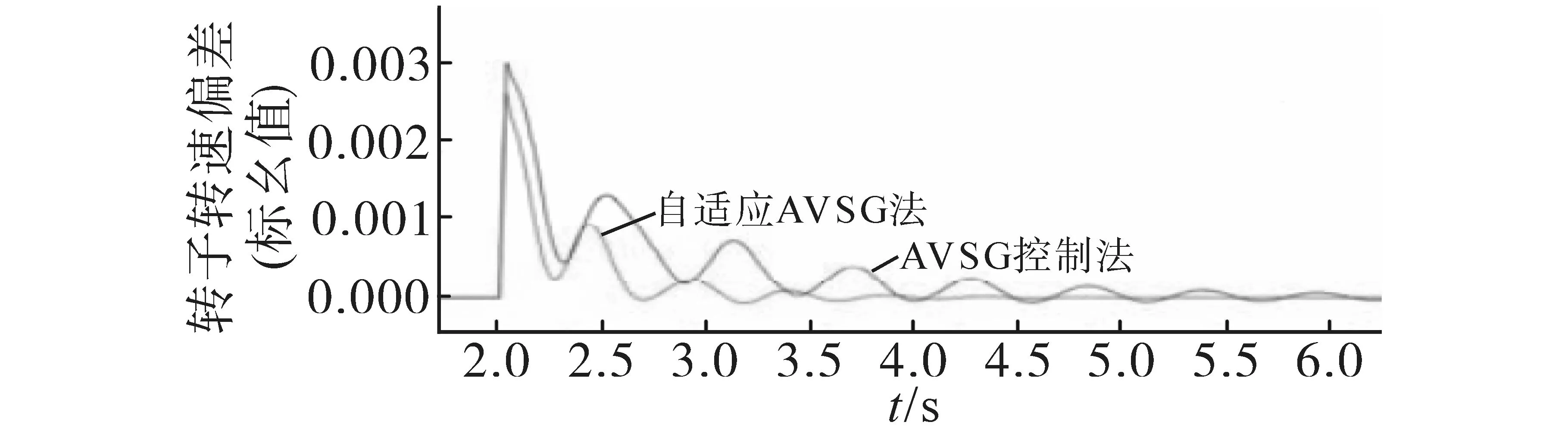
图15 发生故障时转子转速响应变化Fig.15 Rotor speed response change in the event of a fault
5 结论
鉴于直流微网系统惯性低、且直流系统母线电压抗干扰能力弱的问题,本文提出了一种模拟同步发电机特性的控制策略,并结合荷电状态对下垂控制系数进行调整,得到了基于自适应AVSG 控制方法,根据下垂控制特性曲线的平移操作来调整虚拟同步电机有功分配方式。通过仿真结果得出,基于自适应下垂控制特性的AVSG控制策略能有效避免下垂控制系数变化过程中可能出现的系统失稳风险,有效地分配系统有功并调整直流系统的荷电状态,从而确保风储发电单元持续支撑含可再生微网系统的稳定运行。

