波形钢腹板组合梁桥转向块空间应力仿真分析
周晓夫
(四川省交通勘察设计研究院有限公司,成都 610000)
波形钢腹板组合梁桥没有腹板束的布置空间,需采用体外预应力束来承受二期恒载和活载,而转向块是体外预应力束的关键传力构件之一,由于其结构异形、受力复杂,很容易成为设计的薄弱点,甚至成为安全隐患。目前,基于转向块的研究还不是很充分,有必要进行深入探讨。
本文以西北某大桥为工程背景,大桥采用(57+100+100+57)m波形钢腹板连续刚构桥型,分别在边跨和中块各设置了2组和4组转向块来实现体外预应力束的转向,转向块采用横隔构造形式,具体构造如图1所示。
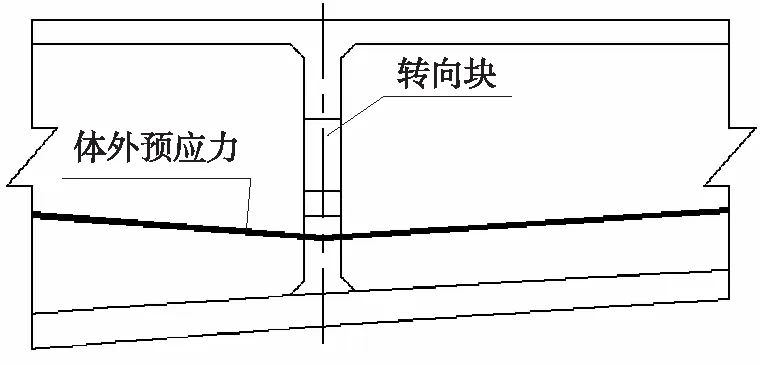
(a)转向块立面
1 转向块实体仿真建模
主要采用以下思路对转向块实体进行仿真分析:
1)采用Midas有限元程序建立整体模型,提取目标单元的内力作为局部实体计算的内力边界条件。
2)采用Ansys有限元程序,依据圣维南原理建立转向块两侧单元的局部实体模型。
3)采用等效荷载的方式模拟预应力体外束对转向块的作用力,并进行受力分析。
1.1 材料参数取值
箱梁及转向块混凝土强度均为C55,体外预应力束采用19孔钢绞线,波形钢腹板采用Q345C钢材,主要材料取值如表1、表2所示。

表1 材料特性值

表2 材料弹模与强度
1.2 有限元模型建立
采用Ansys有限元程序建立转向块及附近梁段的局部实体模型,转向块厚度为50 cm,选取转向块向两端各延伸一个波段作为研究范围,模型结构总长14.4 m。其中,采用Solid45单元模拟混凝土结构、Link8单元模拟预应力钢束、Shell65单元模拟波形钢腹板,有限元模型如图2所示。

图2 转向块局部计算有限元模型
1.3 管道压力大小的确定
采用等效荷载的方式来模拟体外预应力束对转向块产生的作用力,等效荷载采用“脱离体法”来计算。即首先将钢束从预应力结构中剥离出来,根据静力平衡的原理对预应力束进行受力分析,然后将预应力束所承受的作用力作为等效荷载反作用于转向块上。
实际结构中预应力等效荷载以面荷载的形式进行加载,由于荷载作用面积较小,可认为面荷载分布均匀,预应力孔道半圆所需施加的面荷载集度为:
式中:P为垂直于加载面施加的面荷载集度(力/面积);R为孔道曲线半径;r为孔口截面半径;Npe为有效预应力。
按照上述公式,大桥采用19孔钢绞线,张拉控制应力为1 116 MPa,计算可得加载面力为5.01 MPa。将转向块孔道的上表面作为受力面,把体外束张拉力转化成均布节点力垂直加载到该面,体外预应力等效荷载加载如图3所示。

图3 体外预应力等效面荷载加载
1.4 边界条件设置
将模型左侧截面固定,建立以截面质心为主节点的刚域,然后再约束主节点的6个自由度。对模型右侧截面进行外力加载,同时假定钢束与转向块接触面光滑,仅考虑体外束对转向块的竖向分力,不考虑纵向摩阻力。
模型右侧选取3种最不利控制工况进行加载,分别为FY最大、MX最大及FZ最大工况(X为横桥向,Y为竖直方向,Z为顺桥方向),同时还单独提取恒载工况进行计算对比。各工况下的内力来自Midas程序整体计算的结果,局部计算的截面内力边界条件如表3所示。

表3 截面内力边界条件
2 应力计算及结果分析
由于转向块构件主要承受体外预应力的竖向分力,本文主要以FY最大工况下的应力分布云图进行详细分析。云图中应力结果均采用国际制单位Pa,正值为拉应力,负值为压应力。
2.1 横向应力
分别从模型的正面(端向)和背面(跨向)提取了转向块横向应力的分布云图,如图4、图5所示,以分析其横向应力分布的特点和变化趋势。
从图4及图5可以看出,在FY最大工况下,转向块的最大横向拉应力约为1.9 MPa,分布于转向块下缘体外束转向孔道两侧,该区域的背面则对应分布着约5.7 MPa的横向压应力;孔道两侧接近倒角位置出现的约4.8 MPa拉应力和6.6 MPa压应力峰值属于应力集中造成的失真应力,不予考虑。

图4 X向正应力云图(端向)

图5 X向正应力云图(跨向)
2.2 竖向应力
分别从模型的正面(端向)和背面(跨向)提取了转向块竖向应力的分布云图,如图6、图7所示,以分析其竖向应力分布的特点和变化趋势。
从图6及图7可以看出,在FY最大工况下,转向块的最大竖向拉应力约为2.1 MPa,分布在转向块端向下缘和跨向上缘,该区域的背面则分布着最大竖向压应力,峰值约8.7 MPa;在转向块两面共8个棱角处,分布有约23 MPa的拉应力和25 MPa的压应力,均属于应力集中造成的失真应力,不予考虑。

图6 Y向正应力云图(端向)

图7 Y向正应力云图(跨向)
2.3 纵向应力
分别从模型的正面(端向)和背面(跨向)提取了转向块纵向应力的分布云图,如图8、图9所示,以分析其纵向应力分布的特点和变化趋势。
从图8及图9可以看出,在FY最大工况下,转向块的上缘局部分布有约8 MPa的纵向压应力,下缘分布有约1.8 MPa的纵向拉应力,其余位置均匀分布有3.5 MPa的纵向压应力;在转向块两面共8个棱角处,分布有约16 MPa的拉应力和19 MPa的压应力,均属于应力集中造成的失真应力,不予考虑。

图8 Z向正应力云图(端向)
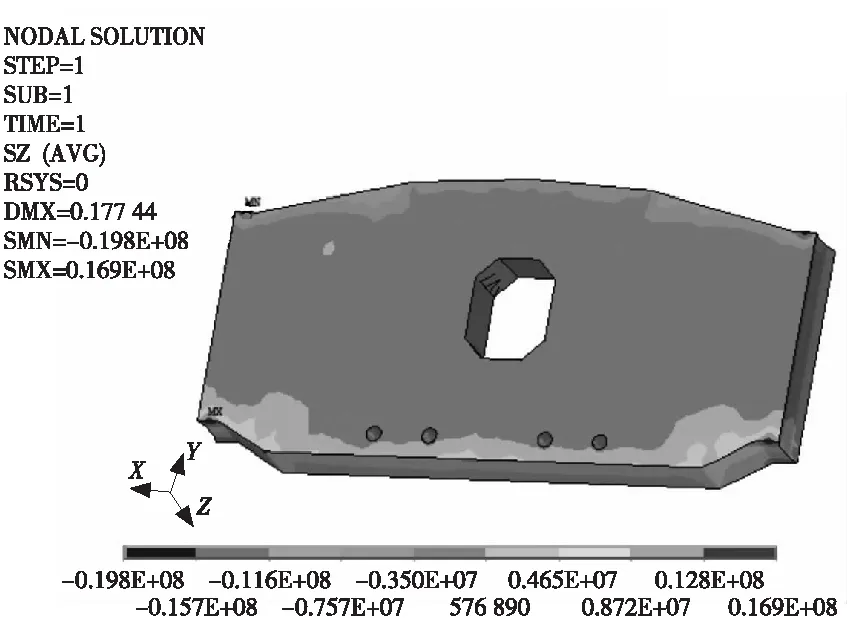
图9 Z向正应力云图(跨向)
2.4 主应力
分别从模型的正面(端向)和背面(跨向)提取了转向块第一、第三主应力的分布云图,如图10~图13所示,以分析其主应力分布的特点和变化趋势。
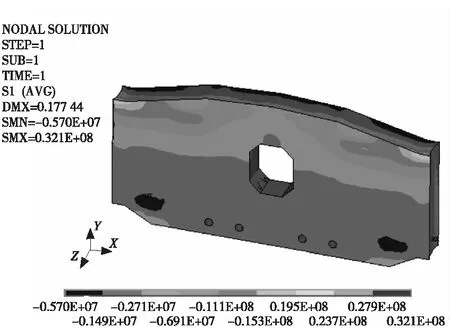
图10 第一主应力云图(端向)

图11 第一主应力云图(跨向)
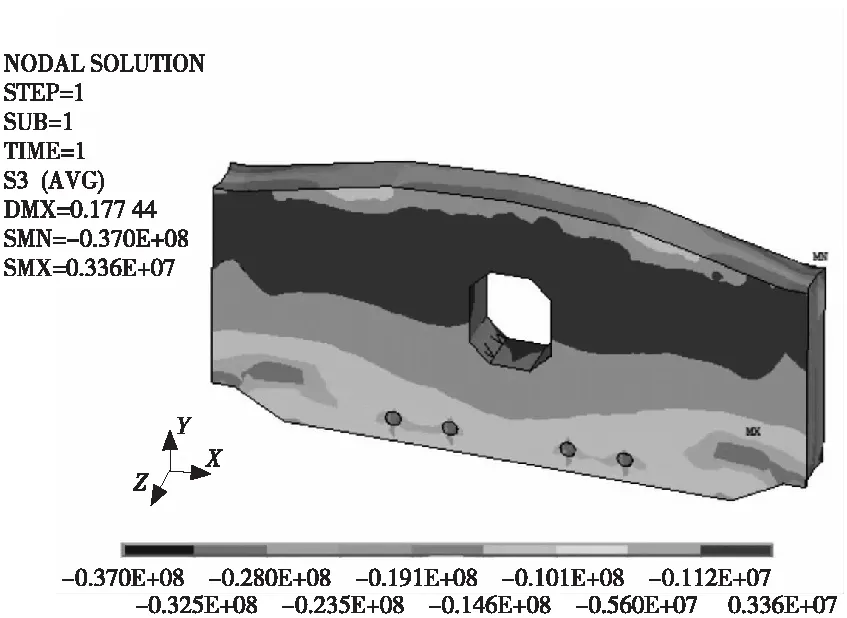
图12 第三主应力云图(端向)

图13 第三主应力云图(跨向)
从图10及图11可以看出,在FY最大工况下,转向块的最大主拉应力约为2.3 MPa,出现在转向块的端向下缘和跨向上缘;该区域的背面则分布最小主拉应力,约为1.5 MPa的压应力;在转向块的上、下缘棱角处以及转向孔道边缘分布有约32 MPa的拉应力及5.7 MPa的压应力,属于应力集中造成的失真应力,不予考虑。
从图12及图13可以看出,在FY最大工况下,转向块的最大主压应力峰值约为10.1 MPa,出现在转向块的端向上缘和跨向下缘;该区域的背面则分布最小主压应力,约为1.3 MPa;孔道上方分布有突变的压应力,约为5.6 MPa;在转向块的上、下缘棱角处应力集中现象明显,分布有约3.3 MPa的拉应力和37 MPa的压应力,属于应力集中造成的失真应力,不予考虑。
2.5 4种工况计算结果分析
4种控制工况下,转向块的局部应力峰值汇总如表4所示。

表4 各控制工况下转向块应力峰值汇总 MPa
通过以上计算结果可以发现,每种工况下同类应力的分布情况基本相似,说明转向块的应力分布规律比较明确;同时,除纵向应力之外,其余应力存在明显的拉压分布界限,总体上预应力孔道以上呈受压、以下呈受拉的分布趋势,转向块受力的基本特点和规律如下:
1)转向块与顶底板连接处均分布有竖向拉应力,由于主要承受体外预应力竖向分力的作用,该拉应力在底板连接处最大,往中部逐渐减小,如图6、图7所示。
2)当转向块的预应力管道距离底板较近时,竖向拉应力不能完全向下扩散,应力集中现象非常明显,如图6、图7所示。
3)转向块与顶底板连接的4个角点处拉压应力最为集中,局部计算结果显示角点处压应力已超过混凝土的抗压强度要求,但实际结构中转向块与顶底板连接处都设置有倒角,集中的压应力能通过倒角有效扩散。
4)较大的主拉应力主要分布在与顶底板连接处及孔道周围,有使转向块从梁体内脱离的倾向,如图10、图11所示。
5)转向块下部预应力孔道的外侧一定区域内分布有较大的横向拉应力,如图4、图5所示。
6)转向块与底板连接处分布较大的纵向拉应力,其它位置纵向拉应力数值均较小,且分布较均匀。
7)转向块较大的主拉应力分布在与底板连接处附近一定高度范围,且在孔道下侧有主拉应力集中现象,孔道上侧拉应力部分释放。
8)所有计算是将转向块作为弹性材料来进行分析的,如果考虑材料非线性的影响,局部应力峰值将会有所减小。
3 改变转向块厚度的研究
横隔式转向块本质是一种板式结构,板厚的改变对其受力的影响毋容置疑,但敏感程度需进一步研究。在上述模型的基础上,分别对转向块的厚度增加了20 cm和40 cm,提取实体模型孔道下缘受拉区的竖向正应力结果进行对比,分析结构尺寸改变对转向块设计最为控制的竖向拉应力的影响(转向块几何中心位于纵向坐标7.2 m处),计算结果如图14所示。

图14 不同厚度转向块应力变化趋势
从图14应力变化曲线可以看出,板厚对转向块竖向拉应力的影响是比较敏感的,随着板厚按照20 cm级数递增,其竖向拉应力也按照约0.18 MPa的趋势相应递减。
4 波形钢腹板组合梁桥转向块轻型化设计的建议
波形钢腹板组合梁桥型常用于地震烈度较高的高墩桥梁,希望通过减小梁体自重来达到降低地震响应的目的,故对转向块自重的要求要高于常规体外预应力混凝土桥梁。
该类桥梁的转向块一般要兼作横隔板使用,上述研究虽然已表明加大转向块厚度对改善其受力效果较为明显,但因转向块数量多,可能会导致恒载增加过多对抗震不利;同时如果体外预应力在跨中正弯矩区的布束位置过于靠近形心,虽然有利于转向块下缘应力集中的释放,但又会造成整体结构的预应力效率偏低。结合转向块的受力特点,提出针对波形钢腹板组合梁桥转向块设计轻型化的几点建议:
1)转向块可采用下厚上薄的变厚度构造形式,依靠较大尺寸来抵抗孔道下缘的竖向拉应力,也利于应力集中的释放,而上部以受压为主,往往不控制设计,可适当减小厚度来减轻自重。
2)转向块可考虑仅采用下部连接的半高度结构形式,在满足自身受力的前提下,通过与梁体间设置可靠的横、竖向连接钢筋,结构的高度只需能克服主拉应力使转向块从梁体内脱离即可,这样也可减轻自重。
3)转向块可考虑采用钢结构形式,以钢材优异的抗拉、抗压性能完全可保证转向块满足承载力的要求,较好地实现构造轻型化。
5 结束语
1)转向块广泛分布有竖向拉应力,其中底板连接处最大,往中部逐渐减小,且竖向拉应力是设计主控因素。
2)应合理确定预应力管道与底板的相对位置关系,避免两者过近造成竖向拉应力无法有效扩散,从而产生应力集中。
3)应合理拟定倒角构造尺寸,倒角设置对释放4个角点应力的效果明显。
4)应加强转向块与梁体之间的横、竖向钢筋连接,避免主拉应力造成两者脱离。
5)转向块可以采用变厚度、半高度等构造形式及钢结构方式来实现轻型化设计,以满足波形钢腹板组合梁桥减轻自重的目的。

