基于Engl极小化原则确定Robin系数的数值求解
马衍波,瞿 丹
(韩山师范学院 数学与统计学院,广东 潮州 521041)
考虑带有如下边界条件的Laplace方程:


Robin 反问题解的唯一性可由一致连续原理给定[1],然而,解的存在性需要给定数据的兼容性,而这是不容易证明的.更为困难的是,反问题的解并不连续依赖给定数据,即:给定数据的些许误差可能引发解的巨大变化.虽然如此,由于该模型的广泛应用,仍有众多数学家就Robin反问题的数值求解进行研究[2-7].文献[8]讨论了区域Ω 为窄矩形的数值求解;最小二乘法在反问题的研究中被广泛应用,文献利用有限元分解讨论了正则的最小二乘法,该方法对恢复光滑的Robin 系数是有效的.针对分段常数的Robin系数,文献[9-12]分别利用Modica-Mortola和Kohn-Vogelius函数进行了讨论,实验证明对带有陡峭边界的恢复是有效的.而针对非光滑的Robin系数,基于全变差的非线性反问题的数值方法得到了很多学者的重视[13-18].
由于TV正则化泛函在0点不可导,所以其数值算法的设计是很大的挑战.考虑到Tikhonov正则化方法和TV正则化方法的优缺点,我们给出一种自适应的TV方法,将Tikhonov正则化方法和TV正则化方法的优点结合起来.数值实验表明,该方法对分段常数的Robin反问题的恢复有较好的效果.
1 边界积分方程及其离散化
首先,引入令φ=φ(x,y)为二维Laplace方程的基本解,由格林公式,得到如下积分方程:

该积分方程含有dΓ(x)是定义在边角上的指标函数,满足

定义

假定平面域的边界Γ 为光滑的,即设Γ={z(t):t∈[0,1]},其中,z:R→R2为2π 周期光滑函数,且z为定义[0,1]上的单射函数,满足z′(t)≠0,∀t∈[0,1].令
u(t):=|z′(t)|u(z(t)),t∈[0,1],
可得到参数化的积分算子:


2 自适应泛函

其中
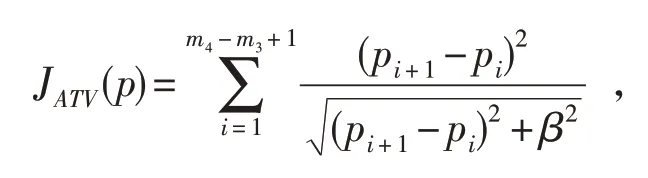
注意:这里的pi是p(ti)的近似值,且p0=0,pm4-m3+1=0.
令
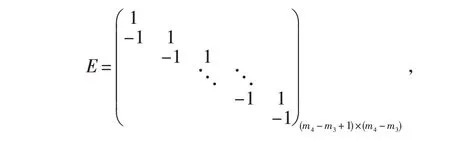
则有

这里Ei表示矩阵E的第i行.
引进向量e(p)=R0A(p)-1f-u0,上述泛函(1)可以简写为残差项和正则项之和:

该正则泛函充分考虑了ROF模型和l2模型的优势:当|pi+1-pi|≪β,说明函数在该点处梯度变化较大,可能存在断点,相应的正则分量接近|pi+1-pi|,可以充分利用TV正则的优势处理断点的恢复;而|pi+1-pi|≪β说明函数在该点处梯度变化不大,此时相应的正则分量接近||pi+1-pi||2/β,故此时可以充分利用l2范数模型的优势,使得近似解具有一定的光滑性.
3 数值实验
在下面的数值试验中,假设椭圆具有标准参数:
x=x(t)=(acos(2πt),bsin(2πt)),0 ≤t≤1,
固定a=1,b是一个可以任意取值的参数.两个不相交的区域Γ0,Γ1分别为

函数g(t)满足

为了比较方便,选择了两种Robin函数p(t),这两种函数在文献[9]中进行验证.
测试是用Matlab进行的.在参数区间[0,1]上设置均匀分区,取步长h=0.002 5.在下面的所有测试中,首先选择p(t),并通过求解相应的离散系统,

在网格点t1,t2,…tn处利用高斯消元法得到(4)解的近似值,这里A(p)来自于公式(1).然后,用得到的u|Γ来产生u0,并添加一定的随机噪声:

其中符号“rand”表示区间(0,1)上均匀分布的随机数,δ是噪声级别.在所有的测试中,总是选择初始值p0=(0.5,0.5,…,0.5)T.
正则化参数在求解不适定问题中起着重要作用,利用基于Engl原理获得一个有效的正则化参数,尤其当数据的噪声级有准确的估计值时.然而,参数α的值可能在稍大的范围内变化.在我们的数值实验中,假设已知误差E:=||R0u-u0||的近似估计.首先选择了一个初始参数α,然后根据||R0u-u0||2的值更新α.准确地说,如果||R0u-u0||2>E,将α替换为0.5α;如果||R0u-u0||2 利用Engl原理,得到恢复的Robin系数,效果见图1.其中噪声水平为5%,迭代次数分别为35和50次.图2给出了两种Robin系数恢复过程中的相对误差. 图1 Robin系数恢复效果 图2 相对误差随迭代次数的变化 自适应的TV泛函充分考虑了TV模型和l2模型的优势,在可能存在断点的地方,充分利用TV正则的优势处理断点的恢复;而在不是断点的地方,可以充分利用l2范数模型的优势,使得近似解具有一定的光滑性.数值实验也说明了这一点.

4 结论

